APLICATION OF THE TDS TECHNIQUE FOR DETERMINING THE AVERAGE RESERVOIR PRESSURE FOR VERTICAl WELLS IN NATURALLY FRACTURED RESERVOIRS

Molina, Miguel-D; Escobar, Freddy-Humberto; Montealegre M, Matilde; Restrepo, Dora-Patricia

Services on Demand

Journal

Article

Indicators

Cited by SciELO
Access statistics

CT&F - Ciencia, Tecnología y Futuro

Print version ISSN 0122-5383On-line version ISSN 2382-4581

C.T.F Cienc. Tecnol. Futuro vol.3 no.1 Bucaramanga Jan./Dec. 2005

APLICATION OF THE TDS TECHNIQUE FOR DETERMINING THE AVERAGE RESERVOIR PRESSURE FOR VERTICAl WELLS IN NATURALLY FRACTURED RESERVOIRS

Aplicación de la técnica TDS en la determinación de la presión promedio del yacimiento en pozos verticales de yacimientos naturalmente fracturados

Miguel-D. Molina¹, Freddy-Humberto Escobar², Matilde Montealegre M.², and Dora-Patricia Restrepo³

¹Ecopetrol S. A - Instituto Colombiano del Petróleo, A. A. 4185 Bucaramanga, Santander, Colombia

² Universidad Surcolombiana, Programa de Ingeniería de Petróleos, Grupo de Investigación en Pruebas de Pozos

³Universidad Nacional de Colombia, - Sede Medellín - Facultad de Minas, Medellín, Colombia

e-mail: fescobar@usco.edu.co

(Received 3 March 2005; Accepted 28 November 2005)

Abstract: Average reservoir pressure is used for characterizing a reservoir, computing oil in place, performing reservoir monitoring by material balance, estimating productivity indexes and predicting future reservoir behavior and ultimate recovery. It is truly important to understand much reservoir behavior in any stage of the reservoir life: primary recovery, secondary recovery and pressure maintenance projects. The average reservoir pressure plays a critical role in field appraisal, well sizing, and surface facilities sizing. Almost every well intervention job requires the knowledge of this parameter.

No significant research was conducted during the last three decades on the determination of the average reservoir pressure. The majority of the existing methods for determining average reservoir pressure are based on conventional analysis and some of them use correction plots for specific reservoir shapes which made them of low practicity. A new methodology based on the Tiab Direct Synthesis (TDS) technique uses the pressure derivative for determination of the average reservoir pressure was introduced very recently for vertical and horizontal wells in homogeneous reservoirs. This technique has been extended to naturally fractured formations using information from the second straight line of the semilog plot.

By default, all reservoirs are naturally fractured; estimating the average reservoir pressure for homogeneous reservoirs should be a specific case of naturally fractured reservoirs. Currently, the inverse procedure is performed. Therefore, in this article a new, easy and practical methodology is presented for the first time, estimating average reservoir pressure for naturally fractured reservoirs (heterogeneous systems) during pseudosteady-state flow period for vertical wells located inside closed drainage regions. This technique employs a new analytical equation which uses a single pressure point and the value of the pressure derivative corresponding to the late time pseudosteady state period eliminating the use of correction charts and type-curve matching.

We verified the proposed technique with simulated cases for values of the interporosity flow parameter, Λ, of 1 and the storativity coefficient, , of 0 (homogeneous reservoir) and successfully compared to traditional techniques and by the application to one field case. This technique (Tiab, 1995) is accurate since it uses an exact analytical solution and matches very well the results from conventional analysis. It is also more practical and much easier to use than conventional analysis.

Keywords: double porosity systems, pseudosteady state regime, bounded reservoir, average reservoir pressure, interporosity flow parameter, strorativity coefficient, and reservoir area.

Resumen: La presión promedia del yacimiento se usa en caracterización de yacimientos, para calcular petróleo original, efectuar monitoreo del yacimeinto mediante balance de materia, estimar índices de productividad, y predecir el comportamiento y recobro final de un yacimiento. Es de vital importancia entender al máximo el comportamiento del yacimiento a cualquier etapa de su vida: recuperación primaria, secundaria y proyectos de mantenimiento de presión. La presión promedia juega un papel crítico en evaluación de campos, tamaño del pozo y de facilidades de superficie. Casi todo trabajo de intervención al pozo requiere de este parámetro.

Durante las últimas tres decadas se ha efectuado muy poca investigación para determinar la presión promedia del yacimiento. La mayoría de los métodos existentes para su determinación se basan en técnicas convencionales, y algunos de ellos emplean gráficos correctivos para formas de yacimiento específicas lo cual los hace poco prácticos. Recientemente se introdujo una nueva metodología basada en la técnica Tiab Direct Synthesis (TDS) que usa la derivada de presión para determinar la presión promedia en formaciones homogéneas drenadas por pozos horizontales o verticales. Esta técnica ha sido extendida a yacimiento naturalmente fracturado usando información de la segunda línea recta del gráfico semilog.

Por antonomasia, todos los yacimientos son naturalmente fracturados. La estimación de la presión promedia para yacimientos homogéneos debería ser un caso particular de los yacimientos naturalmente fracturados. Actualmente, se realiza el proceso inverso. En este artículo se presenta por primera vez una metodología nueva, fácil y práctica para yacimientos naturalmente fracturados sistemas heterogéneos) durante estado pseudoestable para pozos verticales, localizados en regiones de drene cerrados. Esta técnica usa una nueva ecuación analítica la cual a su vez usa un único punto de presión y derivada de presión correspondiente al flujo pseudoestable tardío, evitando el uso de cartas correctivas y curvas tipo.

La técnica propuesta se verificó con casos sintéticos para valores del parámetro de flujo interporoso, Λ, de 1 y el coeficiente de almacenaje, ?, de 0 (yacimiento homogéneo) y se comparó satisfactoriamente con las técnicas convencionales y a la aplicación de un caso de campo. Esta técnica (Tiab, 1995) es exacta puesto que utiliza una solución analítica directa y se ajusta muy bien con los resultados obtenidos por el método convencional. La técnica es más práctica y fácil de usar que el método convencional.

Palabras clave: sistemas de doble porosidad, régimen de estado seudo-estable, yacimiento cerrado, presión promedia de yacimiento, parámetro de flujos entre porosidades, coeficiente de almacenaje y área de reservorio.

INTRODUCTION

Chacon et al. (2004) have recently introduced a technique to estimate reservoir average pressure for vertical and horizontal wells using the pressure derivative curve but eliminating type-curve matching. Later, Molina et al. (2005) presented a first approach to estimate average reservoir pressure in heterogeneous reservoirs. Both methods are based upon reading unique characteristic points or features found on the pressure and pressure derivative plot which are then used to develop analytical equations (Tiab, 1995).

An extension of the TDS technique has been used in this work to determine the average reservoir pressure for a closed and circular double-porosity system which is produced by a vertical oil well. For this purpose, two new analytical solutions involving the interporosity flow parameter, Λ and the storativity coefficient (Warren and Root, 1963) ?, under pseudosteady-state conditions are presented. Model one involves the reservoir drainage area including several shape factors, and model two is obtained from a straight forward algebraical manipulation which leads to an easier solution which does not include the drainage area. The proposed technique was successfully tested by solving simulated examples and a field example, and compared to traditional methodologies.

MATHEMATICAL FORMULATION

Using the governing equation or a slightly compressible fluid in a bounded reservoir, the average reservoir pressure can be derived based on the fact that production rate is equal to depletion rate; mathematically:

The above equation, at very late times, is transformed to (Djebrouni, 2003):

It can be shown that during pseudosteady state flow (Tiab, 1995) for a close circular reservoir, the pressure behavior is given by:

The late time pressure solution and its pressure derivative for naturally fractured formations are given by (Djebrouni, 2003):

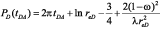
Dividing Equation 4 by Equation 5, it results:

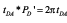
Based up Equation 2, the above equation becomes:

With the purpose of translating the solution in oil-field unit, the following dimensionless quantities are introduced (Earlougher, 1997):

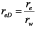
Substituting Equation 8a, 9 and 10 into Equation 7, knowing that any time after closing the well for a buildup test, Pws = P_wf + ?P, and solving explicitly for the average pressure during pseudosteady state (pss) gives:

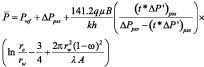
In Equation 11a, the values of ?Ppss and (t*?P’)pss are obtained from the pseudosteady state at any arbitrary time t_pss. In order to include drainage areas of different shapes, the Dietz shape factor is introduced in the previous equation. Recall that C_A for a circular drainage area is equal to 31.62, then:

When the initial reservoir pressure is known, the dimensionless pressure can also be expressed as:

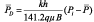
then, Equation 11b becomes:

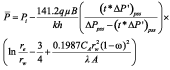
Equation 11a is of more practical use since P_wf is always known in any pressure buildup test. Parameter C_A in Equation 11b and 11c can be approximated by the analytical solution presented by Chacon et al.(2004), as follows:

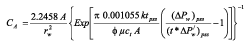
In this study, we also present another mathematical approach which may be applied for cases in which the drainage area is unknown. By equating Equation 3 and 4, we have:

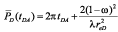
Dividing Equation 12 by Equation 5, it yields:

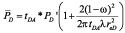
Substituting Equation 8, and 10 into Equation 13 and solving explicitly for the average pressure gives:

As before, any time after closing the well for a buildup test, Pws = Pwf + ?P. For late time, during pseudosteady state (pss), we obtain the following solution:

Average pressure values obtained from Equations 14 and 15 and 11.a and 11.b do not have to coincide since the assumptions are not the same. However, the results should be close to each other.

TDS PROCEDURE

A summary of the procedure will be presented next along with the average pressure estimation. Therefore, steps 1 through 5 are presented with greater detail in Earlougher (1997), and Engler and Tiab (1996) which should be reviewed for completeness. An important advantage of the TDS technique is that most of the reservoir parameters can be obtained more than once from several sources for verification or comparison purposes as outlined in Tiab (1995), Engler (1995), Engler and Tiab (1996), Tiab (1994), Escobar et al. (2004).

Step 1. Construct a log-log plot of pressure and pressure derivative vs. time.

Step 2. Draw a horizontal line through the radial flow horizontal line, read the value of the pressure derivative, (t*?P’)_r, and estimate permeability using the following equation (Tiab, 1995; Engler and Tiab, 1996):

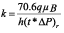
Step 3. The storativity coefficient, ?, can be obtained using either the coordinates of minimum pressure derivative, minimum point, tmin, (t*?P’)_min, the end time of the first radial flow regime, te1, or the starting time of the second radial flow regime, tb2 by using the following relationships introduced by Engler and Tiab (1996):

Step 4. The interporosity flow parameter, ? can be easily estimated from the t_min using an equation presented by Tiab and Escobar (2003):

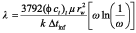
Step 5. Read the pressure value, ?P_r, at any convenient time, t_r1, during the first radial flow regime or t_r2, during the second radial flow regime and compute skin factor (Tiab, 1995; Engler and Tiab, 1996).

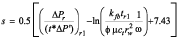
Step 6. The well drainage area is estimated by drawing a unit-slope line through the late time pseudosteady- state points and read the intersection time between this and the radial flow line (drawn in step 2), t_rpi, and estimate the drainage area using the following expression (Tiab, 2003):

Step 7. Take any point convenient on the late pseudosteady-state flow regime and read the time, pressure and pressure derivative: t_pss, ?P_pss and (t*?P)_pss and calculate the average reservoir pressure using Equation 11.a, 11b or 11c.

EXAMPLES

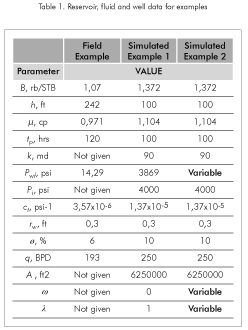
Field example

A pressure buildup test was run in a naturally fractured reservoir located on the superior basin of the Magdalena River in the center of Colombia (South America). Relevant information concerning this well, reservoir and fluid is given Table 1 and the pressure data is provided in Table 3. Estimate the average reservoir pressure using the methods MBH, MDH, Dietz, and Azari and the TDS technique.

Solution

Step 1. A log-log plot of pressure and pressure derivative vs. time is given in Figure 1.

Step 2. From Figure 1, the value of the pressure derivative during radial flow, (t*?P’)_r, is equal to 5,9822 psi. Using s a permeability of 9,7928 md is obtained.

Step 3. From Figure 1, t_min = 14,5041 hr and (t*?P’)_min = 4,5253 psi were read. A storativity coefficient, ?, of 0,4327 is obtained from. Equation 17.

Step 4. Using Equation 9, the interporosity flow parameter, ?, is 2,996x10-⁷.

Step 5. For estimation of skin factor the following values were read from Figure 2. ?P_r = 33,9603 psi at t_r1 = 6,7142 hr. from Equation 20a, s = -4,85.

Step 6. A value of t_rpi of 73,8645 hrs is obtained. Then, A = 264,4642 acres is found from Equation 21.

Step 7. The following information was read from Figure 2. t_pss = 104,2605 hr, ?P_pss = 50,17 psi, and (t*?P)pss = 9,0924 psi. Use these data in Equation 11.a, assuming circular geometry, the average reservoir pressure is:

Average reservoir pressures estimated from the other methods are not shown here. Table 2 lists the results obtained using conventional and TDS techniques.

Simulated example 1

Estimate the average reservoir pressure using the conventional techniques, such as MBH, MDH, Dietz, and Azari and the TDS technique as discussed in this study for a simulated test run in a circular homogeneous reservoir (? = 0, ? = 1), using the information provided in Tables 1 and 4.

Solution

Since all the parameters are known but average reservoir pressure, we skip steps 2 through 6.

Step 1. The log-log plot is provided in Figure 2.

Step 7. From the derivative plot the following information is obtained:

t_pss = 18.95 hr, ?P_pss = 45.82 psi, and (t* ?P)_pss = 8.333 psi. Using these data in Equation 11.a gives:

The step-by-step procedure for estimating of the average pressure using the techniques named in Table 2 and 6 will not be shown here. A detailed discussion of these procedures can be found in Tiab (1995), and Engler (1995). Results are shown in Table 2.

Simulated example 2

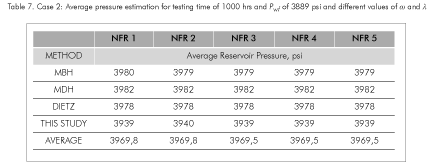
For a sensitivity analysis on the determination of the average reservoir pressure using the methods of MBH, MDH, Dietz, and Azari and TDS technique, five simulated tests for a circular reservoir with different values of ? and Λ were run as reported in Table 5. For these simulations, we used testing times of 100 and 1000 hrs and flowing well pressures of 3889 and 3883 psi, respectively. Reservoir and fluid data are given in the third column of Table 1.

Solution

This example was worked similarly as simulated example 1. In this example, neither pressure data nor plots are provided for space saving and the results are shown in Tables 6 and 7. Notice that, for these simulated cases, the average reservoir pressure estimated using TDS technique matches closely the results from the other methods, and, of course, with the mean value.

RESULTS

It is shown from the given examples that the new technique provides results which fall in the range of the other conventional methods. As seen in Table 2, the value of the average reservoir pressure predicted by the proposed Equation for calculating the average reservoir pressure for naturally fractured reservoirs yields similar results as the conventional techniques.

Several simulations were run for different values of the storativity coefficient and interporosity flow parameter. We found a small influence of these parameters on the estimation of the average reservoir pressure. Results of these simulations are reported in Tables 5 through 7.

CONCLUSIONS

• The TDS is an effective and practical method for calculating the average reservoir pressure from well test data for a vertical well in closed naturally fractured reservoirs for smoothed and noisy data conditions when the late pseudosteady state regime is observed.

• Since traditional models for average pressure estimation considered only the homogeneous case, a new equation, including parameters ? and Λ characteristics of naturally fractured reservoirs, to estimate the average reservoir pressure in naturally fractured formations from transient pressure data is presented and tested with different simulated and field examples and compared to conventional techniques. We found, for simulated cases, the parameters Λ and ? have no influence on the estimation of the average reservoir pressure in naturally fractured reservoirs.

ACKNOWLEDGMENTS

The authors acknowledge the financial support of the Instituto Colombiano de Petróleo (ICP), for financing this study.

REFERENCES

1. Chacón, A., Djebrouni, A. and Tiab, D., 2004. “Determining the Average Reservoir Pressure from Vertical and Horizontal Well Test Analysis Using the Tiab’s Direct Synthesis Technique”. SPE Asia Pacific Oil and Gas Conference and Exhibition, Perth, Australia, SPE 88619.        [ Links ]
2. Djebrouni, A., 2003. “Average Reservoir Pressure Determination Using Tiab’s Direct Synthesis Technique”. M. S. Thesis. The University of Oklahoma, Norman, OK.        [ Links ]
3. Earlougher, R.C., Jr., 1997. “Advances in Well Test Analysis”, Monograph Series, Vol. 5, SPE, Dallas, TX.        [ Links ]
4. Engler, T., 1995. Interpretation of Pressure In Tests in Naturally Fractured Reservoirs by the Direct Synthesis Technique. Ph.D. Dissertation. The University of Oklahoma, Norman, OK.        [ Links ]
5. Engler, T. and Tiab, D., 1996. Analysis of Pressure and Pressure Derivative without Type Curve Matching, 4. Naturally Fractured Reservoirs. J. of Petroleum Scien. and Engineer, 15: 127-138.        [ Links ]
6. Escobar, F. H., Saavedra, N. F., Hernández, C. M., Hernández, Y. A., Pilataxi, J. F., and Pinto, D. A., 2004. Pressure and Pressure Derivative Analysis for Linear Homogeneous Reservoirs without Using Type-Curve Matching. 28^th Annual SPE International Technical Conference and Exhibition, Abuja, Nigeria. SPE 88874        [ Links ]
7. Molina, M. D., Escobar, F. H., Montealegra-M, M., Restrepo, D. P. and Hernandez, Y. A., 2005. Determination of Average reservoir Pressure for Vertical Wells in Naturally Fractured Reservoirs from Pressure and Pressure Derivative Plots without Type-Curve Matching. XI Congreso Colombiano del Petróleo. Bogotá, 2005.        [ Links ]
8. Tiab, D., 1994. “Analysis of Pressure Derivative without Type-Curve Matching: Vertically Fractured Wells in Closed System”, J. of Petroleum Scien. and Engineer, 11: 323-333. Paper originally presented at the 1993 SPE Western Regional Mtg., Anchorage, Alaska, SPE 26138.        [ Links ]
9. Tiab, D., 1995. “Analysis of Pressure and Pressure Derivative without Type-Curve Matching – Skin and Wellbore Storage”. J. of Petroleum Scien. and Engineer, 12: 171. Also, paper presented at the 1993 SPE Production Operations Symposium, Oklahoma City, OK. 21-23, SPE 25423.        [ Links ]
10. Tiab, D., y Escobar, F. H., 2003. “Determinación del Parámetro de Flujo Interporoso de un Gráfico Semilogarítmico”. X Congreso Colombiano del Petróleo. Bogotá, 2005.        [ Links ]
11. Warren, J. E. and Root, P. J., 1963. “The Behavior of Naturally Fractured Reservoirs”. J. of Soc. Petroleum and Engineer, 245-255.         [ Links ]