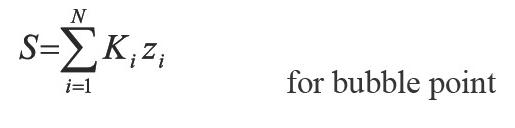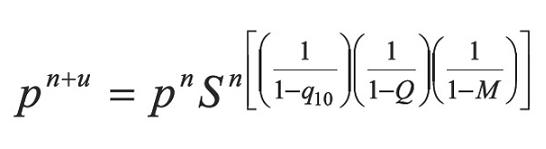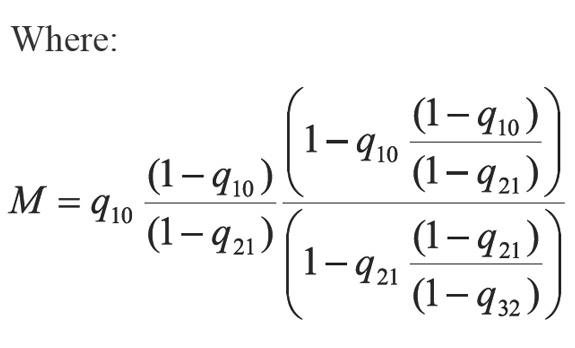Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
CT&F - Ciencia, Tecnología y Futuro
Print version ISSN 0122-5383On-line version ISSN 2382-4581
C.T.F Cienc. Tecnol. Futuro vol.3 no.2 Bucaramanga Jan./Dec. 2006
Juan-Carlos-M. Escobar Remolina1 y Carlos-Alberto Coronado Parra2
1Industrias AVM S.A., Departamento de fluidos 2I & 2D, A. A. 1878, Bucaramanga, Santander, Colombia. e-mail: inydescobar@avm.com.co
2Ecopetrol S.A. – Instituto Colombiano del Petróleo, A. A. 4185, Bucaramanga, Santander, Colombia
(Received May 31, 2006; Accepted Nov. 16, 2006)
ABSTRACT. This paper explains a new method of Super-Accelerated Successive Substitution (SASS) for saturation pressure calculation, in multi-component mixtures of reservoir fluids and synthetic mixtures. The new iterative scheme is characterized by its speed and convergence, even in the critical region. It is easy to implement since it iterates on a single variable, the pressure. In order to demonstrate and to prove the applicability of the new method thirteen samples of fluids were chosen, covering mostly, the most common ranges composition - pressure - temperature (including the critical region) found in phase equilibrium problems in the petroleum industry. This SASS method was compared with other bubble point and dew point calculation methods; such as Conventional Successive Substitution (CSS) and Accelerated Successive Substitution (ASS), and it showed to be faster and more reliable.
Keywords: saturation pressure, reservoir fluid, equation of state (EOS).
RESUMEN. En el presente trabajo se desarrolla un nuevo método de Sustitución Sucesiva Súper Acelerado (SSSA) para el cálculo de las presiones de saturación de mezclas multicomponentes de fluidos de yacimientos y mezclas sintéticas. El nuevo esquema iterativo se caracteriza por su rapidez y convergencia, aún en la región crítica. Es fácil de implementar y además itera sobre una sola variable, la presión. Para demostrar y probar la aplicabilidad del nuevo método se escogieron trece muestras de fluidos, los cuales cubren, en su mayoría, los rangos de composición - presión - temperatura (incluyendo la región crítica) más usuales, encontrados en los problemas de equilibrio de fases en la industria petrolera. Este método de SSSA se comparó con otros utilizados para el cálculo de puntos de burbuja y rocío, tales como la Sustitución Sucesiva Convencional (SSC) y Sustitución Sucesiva Acelerada (SSA), y demostró ser más rápido y confiable.
Palabras clave: presiones de saturación, fluidos de yacimientos, ecuaciones de estado (EOS).
INTRODUCTION
High pressure phase equilibrium computation methods have considerably increased, especially with the use of compositional simulators for describing condensate gases and light oils phase behavior close to or at the critical region (Jiang & Prausnitz, 2000; Firoozabadi & Pan, 2002; Pedersen, Milter, & Sorensen, 2004). Methods have been developed to improve equilibrium calculations, especially isothermal flash and mixtures critical points calculations (Firoozabadi, 1999; Michelsen & Mollerup, 2004). An important computation point such as determining saturation points is still at an important stage of development. Saturation pressure is an important parameter to describe volumetric pressure and hydrocarbon mixture phases. It also determines the type of saturation pressure, that is, if it is a bubble point or a dew point in a Pressure–Temperature diagram (PT) for decision making in reservoir exploitation and production fields. Traditionally, determining bubble points and dew points for a mixture are used to start flash calculations in order to guarantee that specifications are within the two phase region. The standard approach for points or saturation pressures calculation is the partial Newton method, where compositional derivatives are not explicitly considered (Prausnitz et al., 1980). Michelsen (1985) provided ratios using insensibility to the composition of the incipient phase to improve reliability under near-critical conditions, and derive ratios for temperature and maximum pressure on the phases´ limit. Constructions of coexisting sequential curves have found a wide application. Pioneer examples are Asselineau, Bogdanic, and Vidal (1979) and Michelsen (1980) for calculating phase envelopes of mixtures described by an Equation Of State (EOS), and Fredenslund, Sorensen, & Michelsen (1980) who used a fast construction of the bimodal curve for liquid-liquid ternary equilibrium, with the purpose of determining excess energy parameters in Gibbs´s models. Phase envelopes at constant temperatures with total composition, varying linearly between compositions, were built by Nghiem and Li (1984) similar to the ones used by Michelsen. A very original application is the one used Michelsen (1986) to determine ternary mixtures tri-critical points following a three phase region in a fixed manner by decreasing the size of the iterative space. A more recent method to simplify envelopes construction and phases´ saturation pressures was developed by Michelsen (1994), and an example describing extension to multiphase phase limits is given by Pedersen, Michelsen, & Fredheim (1996). In general, in previous methods the saturation pressure problem is defined by a mixture of N-components with feed composition given z, and a specified T temperature, is saturation pressure P and incipient phase y composition, are determined. Since the system is made up of highly nonlinear equations, the problem should be solved by an iterative method. Generally, the Newton-Raphson (NR) method (to update the pressure variable) and the Conventional Successive Substitution (CSS) (to update the incipient variable phase y) are used. In other schemes variables to be updated are the number of components plus two additional variables called ln-values(Ki), temperature and pressure.
Most authors have dedicated themselves to improve or combine previous methods to assure convergence and decrease computation time. Thus, they have developed schemes to accelerate CSS convergence rate (Risnes, Dalen, & Jensen, 1981; Mehra, Heidemann & Aziz, 1983; Michelsen, 1985; Xu, Danesh & Todd, 1992) among others. Type Newton methods are presented by Fussel and Yanosik (1978); Asselineau, et al. (1979); Nghiem and Aziz (1979); Cisternas and Galleguillo (1990). These methods require very approximate initial estimates to the solution to assure convergence. In addition, they consume a lot of computing time in calculating the Jacobian matrix and its inverse, on each iteration level. The CSS method has the advantage that it only iterates over one single variable (or it updates only one variable), at high pressures it may require hundred of iterations to obtain convergence, if it is actually obtained. In this article a Super Accelerated Successive Substitution (SASS) novel process is developed that iterates over one single variable, pressure, as a result of combining equilibrium equations, material balances and simple algebraic equations. The method's results are compared with reservoir fluids saturations pressures and synthetic mixtures experimental data. In addition, it presents comparisons with other methods.
BASIC EQUATIONS
Considering a mixture of N-components of a given composition z and specified temperature T, saturation pressure p, and incipient phase composition y are determined and the following equations in equilibrium:
Where: öi indicate the fugacity coefficient of component i. The above N + 1 equation relate N + 1 variables y and p to specified temperature. Then, the system has a solution. Prausnitz, et al. (1980) defined the following iterative scheme for a conventional successive substitution process at low or moderate saturation pressures:
Where: m is the iteration level and Ki the equilibrium constant or - K value.
Xu et al. (1992) assure that the above method presents very low convergence at high pressures and propose an Accelerated Successive Substitution (ASS) iterative scheme based on the CSS method:
and establish that if the process is convergent, q, should be less than one when S approaches 1 and n tends to 8. This way achieving an accelerating step in saturation pressures calculations. In the following section a super accelerated successive substitution method is developed, to subsequently present the results discussion and finally the conclusions.
PROPOSED METHOD DEVELOPMENT
Taking as starting point Equation 6 the following iterative process of substitution is applied:
Taking logarithms on both sides of the equation and arranging them, we have:
Applying geometric progression concepts to the right member of the Equation 12 the accelerating step in pressure is:
In Equation 13 a new factor (Q) appears allowing to accelerate even more the step given by Equation 6. According to Equations 13 and 14, if the process is convergent, q10 and q21 tend to 0, and then Q tends to 0. The above, when S tends to 1 and n tends to infinite (∞). In developing this work, two more factors that extend Equations 13 were calculated, which are not used in calculations because they increase complexity. For example for one additional factor Equation 13 becomes:
RESULTS AND DISCUSSION
For comparison purposes the CSS (Prausnitz et al., 1980), and the ASS methods were implemented (Xu et al., 1992) along with the proposed super accelerated SASS. Equations of each of the methods (source code) were programmed in C++ language, in a computer with a Pentium 1,0 MHz processor. The Model for the Equation of State (EOS) that predicts vapor - liquid equilibrium is a modification to Redlich-Kwong equation proposed by Soave (1972). Description of the C7+ fraction of all samples selected was performed by a modification of the Gaussian Quadrature proposed by Pelaez and Escobar (1995). The convergent criterion used in the calculations is obtained from the following objective function:
In each iteration, equilibrium constants or - K values are corrected through equation:
In this work, for calculation and analysis purposes, fluids 1 and 2 (Jacoby, Koeller, & Berry, 1959), fluids 3, 4, 5 (Xu et al., 1992), fluids 6, 7, 8 of PVT laboratory reports, and fluids 9, 10, 11, 12 13 (Coronado & Escobar, 2005) were used. All previous fluids present composition data and saturation pressures at given temperatures, from bubble points, going through critical region up to dew points. Table 1 shows the characteristics of the thirteen fluids selected to compare the three calculation methods: SASS, ASS and ASS.
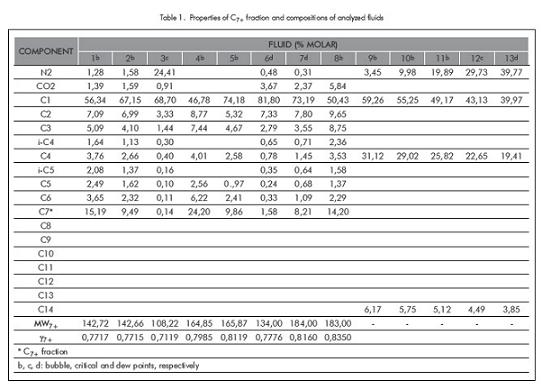
Table 1 also provides the molecular weights and specific gravities for fractions C7+ for the first eight fluids to which characterization of fraction C7+ is applied. As it is shown in Table 1, composition of the 13 fluids cover a wide range, including significant variations of fraction C7+ (fluids 1 to 8) and considerable quantities of nitrogen (synthetic fluids 9 to13). The previous fluids represent volatile, condensate, critical and nearly-critical fluids; it also includes fluids potentially appropriate for nitrogen recovery. Table 2 shows the number of iterations used by each method in calculating saturation pressure at each temperature. According to Table 2 it is shown that in all fluids, the number of iterations required in the SASS is considerably less than the ones used in the CSS and ASS methods. The difference in the number of iterations increases when the critical region is approached or reached, as is demonstrated in fluids 3, 7 and 12 that are near or at the critical point. In Table 2, it is observed that in fluids 3 and 7 for the CSS method 500 iterations were reached and convergence was not obtained or it was extremely slow. For fluid 5 CSS and ASS methods reached a dew point, but the experimental data was reported as bubble point. In the original work, Xu et al. (1992) obtained a bubble point (and not a dew point); this was possibly due to, that the previous authors did not characterize fraction C7+, presenting differences due to specific gravity or that fraction´s molecular weight.
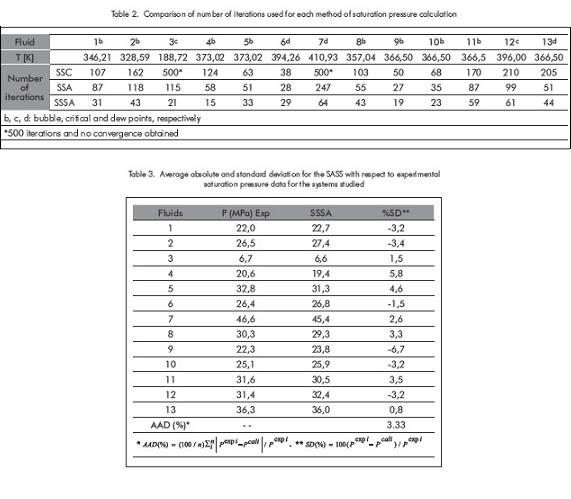
Table 3 shows absolute average deviation (AAD%) and standard deviation (SD%), of the new method for the thirteen samples, with respect to experimental saturation pressure. According to Table 3, the AAD for the SASS has a relatively small value (3,3%) for the fluid systems being studied. In addition, it shows that the SD for each fluid does not exceed 5% in absolute value, except for fluids 4 and 9. From the above mentioned, it could be thought that there is an improvement presented in the predictive ability of the Soave-Ridlich-Kwong EOS model, but the above can also be due to the method of characterization of fraction C7+ or to the SASS iterative method which acts as "zigzag" that is, above or below, in the search for the real answer; see Table 3. As it can be seen, the method consists basically on "accelerating steps" by having three values of S (S0, S1, S2) Equation 13 or 15 are applied. If the fugacity criteria is not obtained, then correct xi and yi with which we calculated S2, and are other three new S (S´0, S´1, S´2) and repeats the acceleration equation. Three terms were selected, because it was proven with 2, 3, 4 and 5 terms. With two terms summations does not show too much stability, for this class of iterations and five terms increase the number of internal accelerating steps of the method. After three terms the variation is not significant and if it makes the calculations extensive, reason why three terms were chosen. In the previous process the values obtained of intermediate saturation pressures, could be above or below the “real value” of the pressure; this causes the intermittence in the SD values.
Figures 1 and 2 show the impact of temperature on the number of iterations required for the three methods to obtain the answer. Figure 1 corresponds to fluid 7, while Figure 2 to fluid 8. In each one of them it can be clearly seen that the increment in number of iterations of the SASS is not considerable when increasing temperature on critical regions. In the ASS, increment in iterations is marked much more in the critical region. In the conventional successive substitution (CSS) as temperature rises toward the critical region, the number of iterations increases sharply up to the point of not obtaining convergence.
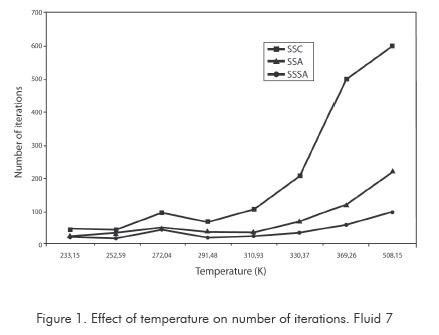

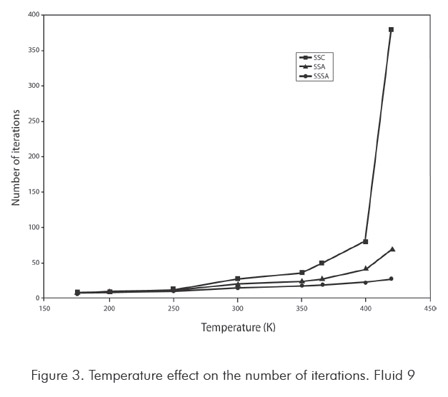
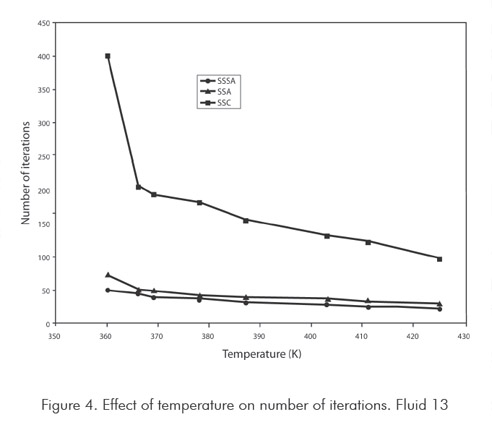
Figures 3 and 4 show functionality of number of iterations with respect to temperature, used by method in calculating saturation pressure. Figure 3 corresponds to synthetic fluid 9 and Figure 4 to synthetic fluid 13. For synthetic fluid 9 saturation pressures points corresponding only to bubble pressure were calculated, from very low pressure (5 MPa) up to a bubble point pressure near the mixture critical point (20 MPa). As shown in Figure 3 increment in SASS iterations is not considerable when increasing temperature to critical regions. In ASS, iterations increase is sharp when approaching the critical point. In the conventional successive substitution (CSS) as temperature rises toward the critical region, the number of iterations increases greatly, up to the point of not obtaining convergence. For mixture 13, only dew points were calculated, from intermediate pressure (25 MPa) up to dew point pressure nearly-critical (36 MPa). As shown in Figure 4 increase in number of SASS iterations are not considerable with temperature. In ASS and CSS, the number of iterations is sharp when approaching the critical point. Behaviors of temperature with number of iterations show a similar behavior to the analyzed fluids, and are not shown in this work. As it can be concluded from the previous analysis, the new method developed in this study promises to decrease a major part of computing time required for compositional simulations of reservoirs. In this type of calculations it could be required to execute between 1 000 000 to 100 000 000 runs of this type or similar type of runs, being evident the usefulness and advantages of the method.
CONCLUSION
• The SASS method is proposed for calculating saturation pressures when EOS are used. The method iterates on a single variable, pressure. The SASS scheme was compared with other methods, CSS and ASS, using thirteen reservoir fluid samples and synthetic mixtures and it showed to be faster, convergent and reliable. The SASS promises to be of very useful in compositional simulation where equilibriums are handled with EOS models, and a great part of computer time is consumed in these calculations.
AKNOWLEDGEMENTS
The author Juan Carlos Escobar, expresses his sincere gratefulness to the department 2I + 2D of Fluids of Industries AVM S.A. in special to Mr. Víctor Julio Gonzalez and the Engineer Miguel Díaz, for their valuable cooperation. The author Carlos Coronado express his sincere gratitude the Lab. PVT of Instituto Colombiano del Petróleo -ICP-Ecopetrol S.A., for their valuable cooperation.
REFERENCES
Asselineau, L., Bogdanic, G., & Vidal, J. (1979). A Vesatile algorithm for calculating vapor-liquid equilibria. Fluid Phase Equilibria, 3: 273-290. [ Links ]
Cisternas, L. A., & Galleguillo H. R. (1990). Constantes de equilibrio de la vaporizacisn. Ingeniería Química (Febrero), 207-212. [ Links ]
Coronado, C. A., & Escobar, J. C. M. (2005). Experimental study and calculations of the near critical behavior of a synthetic fluid in nitrogen injection. CT&F - Ciencia, Tecnología y Futuro, 3 (1), 127-137. [ Links ]
Firoozabadi, A. (1999). Thermodynamics of Hydrocarbon Reservoir. McGraw-Hill, New York. Firoozabadi, A., & Pan, H. (2002). Fast and robust algorithm for compositional modeling: part 1_stability analysis testing. SPE J. 7(1), 78. [ Links ] [ Links ]
Fredenslund, A., Sorensen, J. M., & Michelsen M. L. (1980). Liquid-liquid equilibrium calculations using activity coefficient models. Proc. Secad. Intl. Conf. on Phase Equilibria and Fluid Properties. Berlin. [ Links ]
Fusell, D. D., & Yanosik, J. L. (1978). An iterative sequence for phase-equilibria calculation incorporating the redlich- kwong equation of state. SPEI. (June), 173-182. [ Links ]
Jacoby, R. H., Koeller, R.C., & Berry Jr., V. J. (1959). Effect of composition and temperature on phase behavior and depletion perfomance of rich gas – condensate systems. TRANS., AIME, 216. [ Links ]
Jiang, J., & Prausnitz, J. M. (2000). Critical temperature and pressure for hydrocarbon mixtures from an equation of state with renormalization – grupo theory corrections. Fluid Phase Equilibria, 169 (2), 127-147. [ Links ]
Mehra, R. K., Heidemann, R. A., & Aziz, K. (1983). A Accelerated successive substitution algoritm”. J. Can. Chem. Eng. (August), 590-956. [ Links ]
Michelsen, M. L. (1980). Calculation of phase envelopes and critical points for multicomponent mixtures. Fluid Phase Equilibria, 4 (1-2), 1-10. [ Links ]
Michelsen, M. L. (1985). Saturation point calculation. Fluid Phase Equilibria, 23 (2-3), 181-192. [ Links ]
Michelsen, M.L. (1986). Some aspects of multiphase calculations. Fluid Phase Equilibria, 30: 15-29. [ Links ]
Michelsen, M.L.(1994). A simple method for calculation of approximate phase boundaries. Fluid Phase Equilibria, 98: 1-11. [ Links ]
Michelsen, M. L., & Mollerup J. (2004). Thermodynamic models, fundamentals and computational aspects. Tie-Line Publications. Denmark. [ Links ]
Nghiem, L. X., & Aziz, K. (1979). An robust iterative method for flash calculations using the Soave-Redlich-Kwong and the Peng-Robinson EOS. SPE 8285. [ Links ]
Nghiem, L. X., & Li, Y. K. (1984). Computation of multiphase equilibrium phenomena with an equation of state. Fluid Phase Equilibria, 17 (1), 77-95. [ Links ]
Pedersen, K. S., Michelsen, M. L., & Fredheim, A.O. (1996). Phase equilibrium calculations for unprocessed well streams containing hydrate inhibitors. Fluid Phase Equilibria, 126 (1), 13-28. [ Links ]
Pedersen, K. S., Milter, J., & Sorensen, H. (2004). Cubic equations of state applied to ht/hp and highly aromatic fluids. SPEJ 186. [ Links ]
Pelaez, C. V., & Escobar ,J.C. (1995). Un simulador para el estudio del comportamiento de fases basado en la ecuacisn de estado de soave y calculos de balances de materia. CT&F - Ciencia Tecnología y Futuro, 1 (1), 83-94. [ Links ]
Prausnitz, J. M., Anderson, I., Grens, E., Eckert, C., Hsieh, & O’ Connell, J. (1980). Computer calculation for multicomponent vapor-liquid and liquid-liquid equilibria. Englewood Cliffs, Prentice Hall. Inc. [ Links ]
Risnes, R., Dalen, V., & Jensen, J.I. (1981). Phase equilibrium calculation in the near critical regisn. Dev. Pet. of. Sci, 13: 329-350. [ Links ]
Soave, G. (1972). Equilibrium constants from a modified redlich-kwong ecuation of state. Chem. Eng. Sci, 27: 1197. [ Links ]
Xu, D. H., Danesh A., & Todd, A. C. (1992). An accelerated successive substitution method for calculation of saturation pressure of multicomponent fluids. Fluid Phase Equilibria, 72: 15-24. [ Links ]