Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
CT&F - Ciencia, Tecnología y Futuro
Print version ISSN 0122-5383On-line version ISSN 2382-4581
C.T.F Cienc. Tecnol. Futuro vol.3 no.3 Bucaramanga Jan./Dec. 2007
EFFECT OF THE PSEUDOTIME FUNCTION ON GAS RESERVOIR DRAINAGE AREA DETERMINATION
Efecto de la función de pseudotiempo en la determinación del área de drene de un yaciemiento de gas
Freddy-Humberto Escobar1, Aura-María López2, and José-Humberto Cantillo3
1,2Universidad Surcolombiana, Programa de Ingeniería de Petróleos, Grupo de Investigación en Pruebas de Pozos, Neiva, Huila, Colombia e-mail: fescobar@usco.edu.co e-mail: auramaria3@hotmail.com
3Ecopetrol S.A.-Instituto Colombiano del Petróleo, A.A. 4185 Bucaramanga, Santander, Colombia e-mail: jose.cantillo@ecopetrol.com.co
The gas flow equation is normally linearized to allow the liquid solution of the diffusivity equation to satisfy gas behavior when analyzing transient test data of gas reservoirs. When wellbore storage conditions are insignificant, drawdown tests are best analyzed using the pseudopressure function. On the other hand, buildup pressure tests require linearization of both pseudotime and pseudopressure. It is not the case for the TDS technique which is indifferently applied to either drawdown or buildup tests. However, whichever the case, pseudotime has certain effect at very long testing times in formations of moderate to high permeability.
In this paper, we implemented the Tiab’s Direct Synthesis (TDS) technique, to include pseudotime effects, and observe its influence on the interpretation results of gas well test data at early and late time periods. New analytical equations to estimate reservoir permeability, wellbore storage coefficient, pseudoskin factor and reservoir drainage area are presented. Then, a comparison of results against rigorous time was carried out for simulated and field cases. We found acceptable results for permeability, pseudoskin factor and wellbore storage coefficient. However, for the case of reservoir drainage area, the deviation error was of 4,1% for a simulated case and 17,9% for a field case. However, the smaller of these deviations may be small if related to pressure transient analysis results. However, this deviation in a gas reservoir with reserves of one tera standard cubic feet is equivalent to a huge difference of 38 gigas of standard cubic feet of gas which may have an economic impact to any oil company.
Keywords: reservoir gas, pressure, TDS technique, steady state, permeability, radial flow, mathematical models.
Normalmente, la ecuación de flujo de gas se linealiza para permitir que la solución de difusividad de los líquidos satisfaga el comportamiento del gas cuando se analizan pruebas de presión en yacimientos gasíferos. Las pruebas de declinación de presión se analizan mejor usando la función pseudopresión, cuando los efectos de almacenamiento de pozo son insignificantes. Por otra parte, las pruebas de restauración de presión requieren la linealización tanto de la pseudopresión como del pseudotiempo. Sin embargo, cualquiera que sea el caso, la función de pseudotiempo presenta ciertos efectos a tiempos de prueba muy largos en formaciones de permeabilidad moderada a alta.
En este artículo, implementamos la técnica de Síntesis Directa de Tiab, (TDS), para incorporar los efectos del pseudotiempo, y observar su influencia en los resultados de interpretación de pruebas de presión en yacimientos de gas a tiempos tempranos y tardíos. Se desarrollaron nuevas ecuaciones analíticas para la estimación de la permeabilidad del yacimiento, el coeficiente de almacenamiento del pozo, el factor de pseudodaño y el área de drenaje del pozo. Luego, para casos de campo y simulados, se efectuó una comparación de los resultados contra aquellos donde se usa el tiempo riguroso o normal. Encontramos valores aceptables de permeabilidad, pseudo factor de daño y coeficiente de almacenamiento. Sin embargo, para el área de drene del pozo, la desviación fue de 4,1 y de 17,9% para un caso de campo. La menor de estas desviaciones es un número que resulta pequeño si lo relacionamos con los resultados producidos en la interpretación de pruebas de presión. Sin embargo, esta desviación en un yacimiento con reservas de un tera de pies cúbicos a condiciones normales equivale a una enorme diferencia de 38 gigas de pies cúbicos a condiciones normales lo cual puede impactar económicamente a cualquier empresa.
Palabras clave: yacimientos de gas, presión, técnica TDS, estado estacionario, permeabilidad, flujo radial, modelos matemáticos.

INTRODUCTION
A very important concept to account for gas flow behavior was introduced by Al-Hussainy, Ramey, and Crawford (1966). This was called the pseudopressure function which basically includes the variation of both gas viscosity and compressibility factor which are combined into a single function. Since the dimensionless time involves the viscosity-compressibility product which, for gases, is a function of pressure, then, Agarwal (1979) developed the pseudotime function and performed a practical application to pressure buildup test in vertical fractured wells. Besides Agarwal (1979), Lee and Holditch (1982) demonstrated the advantages of using the pseudotime function in pressure buildup testing of tight formations.
raham and Warwick (1984), proposed a new formulation called scale-time which is only function of time rather than the function of both time and position as previously defined by Agarwal (1979). They demonstrated easier mathematical manipulations but did not provide practical advantages related to well tests.
Later, Spivey and Lee (1986) found the necessity of applying the pseudotime function to linearize the equations under prevalent conditions of wellbore storage during the interpretation of pressure buildup tests and use both pseudotime and pseudopressure for drawdown cases. They utilized type-curve matching for well test interpretation purposes.
To simplify the estimation of the pseudotime function, Aminiam, Ameri, Abbitt, and Cunningham (1991) presented an analytical expressions with the aid of polynomial regression analysis so that the pseudotime function could be easily estimated. They found a deviation of 0,3% which is an adequate range for engineering applications.
In this work, the application of the pseudotime function concept is applied to further extend the application scope of the TDS technique. The study presents new analytical equations for reservoir permeability, pseudoskin factor, wellbore storage coefficient and reservoir drainage area as a function of the pseudotime function. Afterwards, both field and numerical examples were used to test the variation of the above named parameters obtained from the solutions of this study and compared against the solution using actual time, as proposed by Nuñez, Tiab, and Escobar (2002, 2003). It was found that the reservoir drainage area was affected more than the remaining parameters (permeability, pseudoskin factor and wellbore storage coefficient) which impact was irrelevant.
MATHEMATICAL DEVELOPMENT
Agarwal (1979) introduced the pseudotime function to account for the time dependence of gas viscosity and total system compressibility:

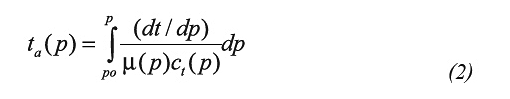
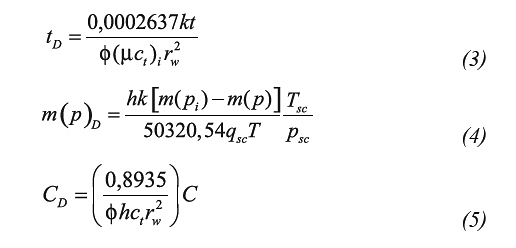
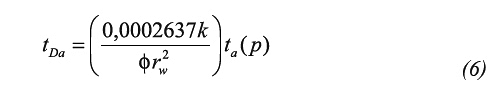
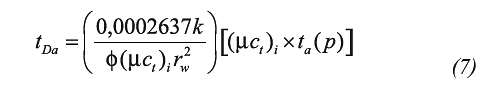
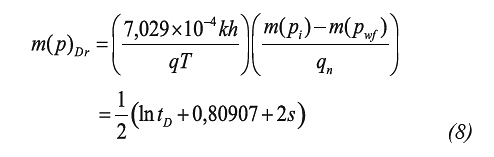
1. The early unit-slope line originated by wellbore storage is described by the following equation:

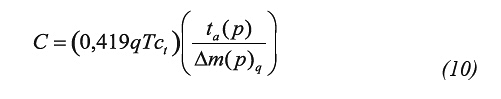


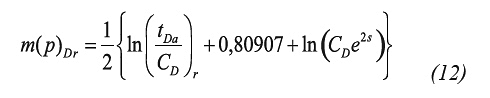

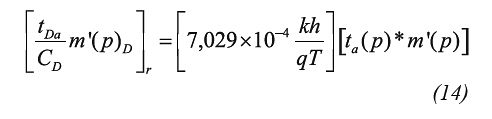
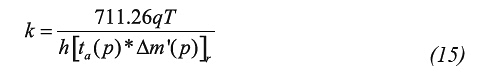
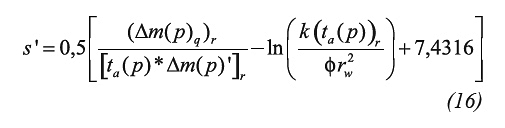
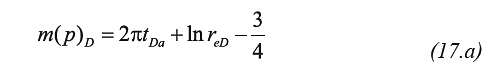



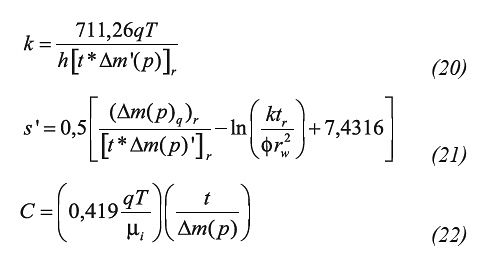

STEP-BY-STEP PROCEDURE
Detailed explanation of the appropriate use and application of the TDS technique are presented by Tiab (1993, 1995), Tiab (1993, 1994), Nuñez et al. (2002), Nuñez et al. (2003). A summarized procedure is outlined as follows:
Step 1. Construct a log-log plot of Δm(p) and ta*Δm(p)' versus ta.
Step 2. Identify the different flow regimes and draw the horizontal line along both radial flow and the unit-slope line. For the later case, the lines is drawn through both the wellbore storage points and the late pseudosteady-state regime, if given the case.
Step 3. Read the intersection point of the wellbore storage line and the radial flow line, (tai, Δm(p)i), note that: Δm(p)i = (ta*Δm(p)’)i = (ta*Δm(p)’)r and find the wellbore storage coefficient from Equation 10 and the permeability from Equation 15. Permeability ought to be verified with Equation 11.b using the pseudotime of intersection of the early unit-slope and the radial lines.
Step 4. Select any convenient pseudotime during radial flow, ta(p)r and read the corresponding Δm(p)r value, then, determine the pseudoskin factor, s’, using Equation 16.
Step 5. Read the intersection pseudotime, ta(p)pss, of the late pseudosteady-state flow regime and the horizontal straight line an determine reservoir drainage area with Equation 19.
EXAMPLES
Field example 1
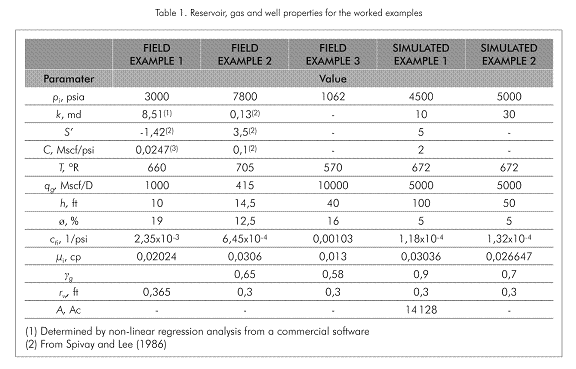
Lee (1982) presented a drawdown test ran in a gas reservoir. The reservoir, gas and well data are given in Table 1. It is required to estimate reservoir permeability, pseudoskin factor, and wellbore storage coefficient using the TDS technique for both real time and pseudotime.
Solution
Once the pseudopressure and pseudotime were estimated, Figures 2a and 2b were constructed. An average radial flow line was drawn.The chosen points read from these plots were:
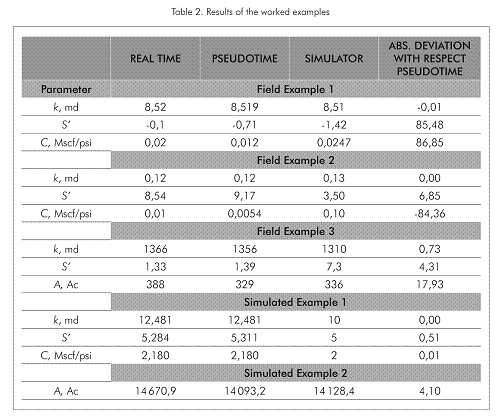
Using Equation 15, 10 and 16, permeability of 8,519 md, wellbore storage coefficient of 0,012 Mscf/psi (0,04928 m3/KPa) and pseudoskin factor of -0,71 were respectively estimated. These same parameters, see Table 2, were also found for the actual time using Equations 20, 21 and 22. Table 2 displays the results of interpreting the test by means of non-linear regression analysis using a commercial software. We are not satisfied with these results because of poor matching between the actual pressure trend and the simulated solution.
Field example 2
Spivey and Lee (1986) presented a drawdown test ran in a gas reservoir. The relevant information for this test is reported in Table 1. Estimate reservoir permeability, pseudoskin factor, and wellbore storage coefficient using the TDS technique for both real time and pseudotime.
Solution
From the pseudopressure and pressure derivative plots, Figures 3a and 3b the following data are read:

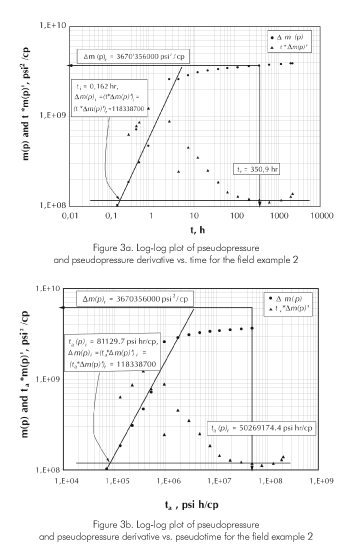
Using Equation 15, 10 and 16, permeability of 8,52 md, wellbore storage coefficient of 0,0054 Mscf/psi (0,02218 m3/KPa) and pseudoskin factor of -0,71 were respectively estimated. Same calculations were performed with using Equation 20 through Equation 22, as reported in see Table 2. That table presents not only the results from this study but also those from Spivay and Lee (1986) which were found by type-curve matching.

Field example 3
A drawdown test was run in a unique well of a Colombian reservoir with pseudopressure and pseudopressure derivative reported in Figure 4a. Information concerning well, fluid and reservoir characteristics required for this test are given in Table 1 along with the other examples. Estimate reservoir permeability, pseudoskin factor, and reservoir area with the TDS technique for both real time and pseudotime.
Solution
The pseudopressure and pressure derivative plots are given in Figures 4a and 4b for real time and pseudotime, respectively. The following data are read:

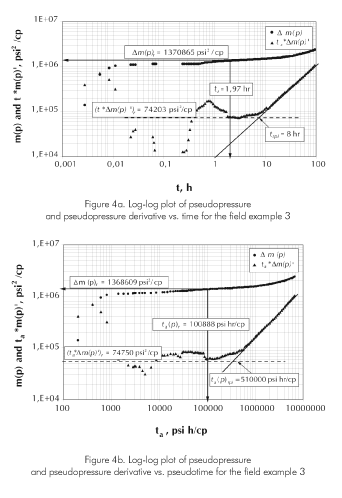
A permeability of 1366 md, pseudoskin factor of 1,33 and reservoir drainage area of 388Ac were determined using Equation 15, 16 and 19, respectively. Besides these, Table 2 also contains the results for the same computations performed using Equations 10, 23 and 21, respectively, of Nuñez et al. (2002).
Simulated example 1
A pressure drawdown test in gas reservoir was simulated using a commercial software with the information of Table 1. Estimate for this system: permeability, pseudoskin factor and wellbore storage coefficient using the TDS technique with both actual time and pseudotime.
Solution
Pseudopressure and pseudopressure derivative are plotted against both actual time in Figure 5a and pseudotime in Figure 5b. The chosen points were:

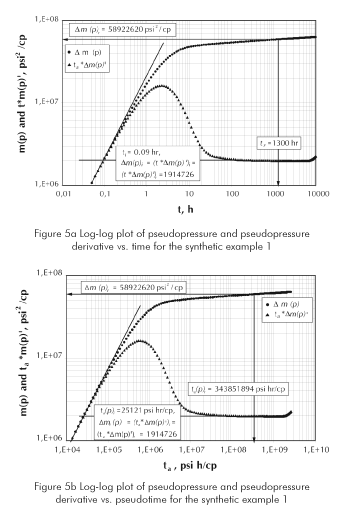
From Equation 15 a permeability of 12,48 md was determined. It was also estimated a pseudoskin factor of 5,31 with Equation 16 and a wellbore storage coefficient of 2,18 Mscf/psi (8,953 m3/KPa) with Equation 10. Practically the same results were obtained using Equations 28.b, 18 and 28.c from the reference of Nuñez et al. (2003).
Simulated example 2
A pressure drawdown test in a closed circular gas reservoir was also simulated using a commercial software based upon the information of Table 1. Estimate the area of this reservoir using the TDS technique and compare to the reference area given in Table 1.
Solution
The simulated values of pseudopressure and pseudopressure derivative against either real time or pseudotime are presented in Figures 6a and 6b, respectively. The intersection point of the radial and late pseudosteady-state lines is found at a pseudotime, ta(p)pri, of 308’763 737,3 h psi/cp (7,664*1018 s KPa/Pa.s) and the corresponding real intersection time, tpri, is found to be 1133 hours (4,076*106 s) from Figure 4b. The area with the rigorous time using Equation 23 was of 14 670,9 Ac. (5,938*108 m2). From Equation 19 the estimated area was 14 093 Ac. (5,704*108 m2).
ANALYSIS OF RESULTS
It is observed, from the worked examples, a good agreement between the simulated values of permeability, pseudoskin factor and wellbore storage obtained using the TDS technique when using either regular time or pseudotime. Practically, same values of permeability, pseudoskin factor and wellbore storage are found no matters if either rigorous time or pseudotime is utilized. However, as expected and exposed formerly in the literature, the estimation of the reservoir drainage area has a higher deviation resulting from the use of real time. The resulting drainage area using real time has an absolute deviation of 4,1% while the one with pseudotime has a deviation of 3,84% with respect to the simulated value. Also the deviation of the area when employing pseudotime has a deviation of 0,25% with respect to the simulated value. From field example 3 was found that the drainage area has an absolute deviation of 17,9% which ir more remarkable. This confirms that the influence of pseudotime is more relevant for long producing times. Although, the deviation value of 3,84% may fall into a widely accepted range of the daily measurements normally obtained from well test analysis, this can introduce significant differences in estimation of reserves.
The non-linear regression analysis simulation conducted using a commercial software did not match perfectly the pseudopressure and pressure derivative curve, therefore, the results may not be as accurate as expected. Consequently, the field cases were not treated in the analysis. Nonetheless, the results of the permeability reference values agree quite well with those from the TDS technique.
CONCLUSIONS
• Estimation of the drainage area in gas bearing formations is affected when the time is used rigorously. We found absolute differences between 4,1 and 17,9% which impacts also gas reserves. Therefore, to assure accuracy, care should be taken into account when interpreting long drawdown pressure tests. For either relatively short drawdown tests or highly low permeability gas formations, regular time may be used for practical purposes without incurring in a significant error.
• Additionally, the TDS technique has been extended by incorporating new analytical solutions, which include the pseudotime function, for the estimation of formation permeability, pseudoskin factor, wellbore storage coefficient and reservoir drainage area. Field and synthetic examples were carried out to test the sensitivity of the mentioned parameters when the pseudotime function is included, as compared to the actual time.
ACKNOWLEDGMENTS
The authors gratefully acknowledge the financial support of Ecopetrol S.A. -Instituto Colombiano del Petroleo (ICP), under the mutual agreement number 008, signed between this institution and Universidad Surcolombiana (Neiva, Huila, Colombia).
REFERENCES
Agarwal, G. (1979). Real gas pseudo-time a new function for presssure buildup analysis of MHF gas wells. Paper presented at the SPE 54th Technical Conference and Exhibition of the Society of Petroleum Engineers of AIME, Las Vegas, NV, Sept. 23-26. SPE 8279. [ Links ]
Al-Hussainy, R., Ramey, H.J., & Crawford, P.B. (1966). The flow of real gases through porous media. J. Petroleum Technol., May. 624-636, Trans. AIME, 237. [ Links ]
Aminiam, K., Ameri, S., W.E., Abbitt, W. E., & Cunningham, L.E. (1991). Polynomial approximations for gas pseudopressure and pseudotime. SPE Eastern Regional Meeting, Lexington, Kentucky, Oct. 22-25. SPE 23439. [ Links ]
Graham, J. W., & Warwick, M. K. (1984). Scaled – time: a new pseudotime function for approximately linearizing gas reservoir models. Unsolicited Paper SPE 13418. [ Links ]
Lee, J., 1982. Well Testing. SPE textbook series (Vol. 1). [ Links ]
Lee, W. J., & Holditch, S. A. (1982). Application of pseudotime to buildup test analysis of low-permeability gas wells with long-duration wellbore storage distortion. J. Petroleum Technol., 2877-2887. [ Links ]
Nuñez, W., Tiab, D. & Escobar, F. H. (2002, October). Análisis de presiones de pozos gasíferos verticales con fracturas de conductividad infinita en sistemas cerrados sin emplear curvas tipo. Boletín Estadístico Mensual del ACIPET, pp.9-14. [ Links ]
Nuñez, W., Tiab, D., & Escobar, F.H. (2003). Transient pressure analysis for a vertical gas well intersected by a finite-conductivity fracture. SPE Production and Operations Symposium, Oklahoma City, OK, March 23-25. SPE 80915. [ Links ]
Spivey, J. P., & Lee, W. J. (1986). The use of pseudotime: wellbore storage and the middle time region. SPE Unconventional Gas Technology Symposium, Louisville, Kentucky , May 18-21. SPE 15229. [ Links ]
Tiab, D. (1993). Analysis of pressure and pressure derivative without type-curve matching: 1- skin factor and wellbore storage. SPE Production Operations Symposium, Oklahoma City, OK. March 21-23, SPE 25423, 203-216. Also, J. Petroleum Scien. and Engineer., (1995), 12: 171-181. [ Links ]
Tiab, D. (1993b) Analysis of pressure derivative without type-curve matching: vertically fractured wells in closed systems. SPE Western Regional Meeting, Anchorage, Alaska, May 26-28. Also, J. Petroleum Scien. and Engineer., 11 (1994), 323-333. SPE 26138. [ Links ]
(Received May 30, 2006; Accepted Aug. 13, 2007)














