ABSTRACT

Petroleum reservoirs under primary, secondary or tertiary recovery processes usually experience simultaneous flow of three fluids phases (oil, water and gas). Reports on some mathematical models for calculating three-phase relative permeability are available in the Literature. Nevertheless, many of these models were designed based on certain experimental conditions and reservoir rocks and fluids. Therefore, special care has to be taken when applying them to specific reservoirs. At the laboratory level, three-phase relative permeability can be calculated using experimental unsteady-state or steady state methodologies.

This paper proposes an unsteady-state methodology to evaluate three-phase relative permeability using the equipment available at the petrophysical analysis Laboratory of the Instituto Colombiano del Petróleo (ICP) of Ecopetrol S.A. Improvements to the equipment were effected in order to achieve accuracy in the unsteady-state measurement of three-phase relative permeability. The target of improvements was directed toward to the attainment of two objectives:1) the modification of the equipment to obtain more reliable experimental data and 2) the appropriate interpretation of the data obtained. Special attention was given to the differential pressure and uncertainty measurement in the determination of fluid saturation in the rock samples.

Three experiments for three-phase relative permeability were conducted using a sample A and reservoir rock from the Colombian Foothills. Fluid tests included the utilization of synthetic brine, mineral oil, reservoir crude oil and nitrogen. Two runs were conducted at the laboratory conditions while one run was conducted at reservoir conditions. Experimental results of these tests were compared using 16 mathematical models of three-phase relative permeability. For the three-phase relative permeability to oil, the best correlations between experimental data and tests using Blunt, Hustad Hasen, and Baker's models were obtained at oil saturations between 40% and 70%.

Key words: oil reservoir, unsteady state, multiphase flow, relative permeability.

RESUMEN

Los yacimientos de petróleo que producen bajo procesos de recobro primario, secundario o terciario, usualmente involucran el flujo simultáneo de tres fluidos (agua, aceite y gas). En la literatura se encuentran modelos matemáticos para predecir la permeabilidad relativa al aceite tres fases. Sin embargo, muchos de estos modelos fueron formulados para determinadas condiciones experimentales, y para ciertas rocas y fluidos de yacimiento, por lo cual se debe tener cuidado al aplicarlo a un yacimiento específico. Al igual que en el caso de dos fases, las permeabilidades relativas tres fases pueden ser evaluadas en laboratorio por metodologías estado estable o estado no estable.

En este trabajo se propone una metodología estado no estable para evaluar experimentalmente permeabilidades relativas tres fases, a partir de los equipos que tiene el laboratorio de análisis petrofísicos del Instituto Colombiano del Petróleo (ICP) de Ecopetrol S.A. Para lograr la medición de permeabilidades relativas tres fases estado no estable en el laboratorio de petrofísicos del ICP, se realizaron mejoras en el equipo de medición de permeabilidades relativas con separador trifásico. Las mejoras fueron dirigidas a lograr dos objetivos: modificar el equipo con el fin de obtener datos experimentales más confiables e interpretarlos apropiadamente. Se prestó especial atención a las mediciones del diferencial de presión y a las incertidumbres en las mediciones de saturación de fluidos en la muestra de roca.

Se realizaron tres corridas de permeabilidad relativa tres fases usando una muestra de Berea, y una muestra de roca del Piedemonte Colombiano. Como fluidos de prueba se usaron salmuera sintética, aceite mineral, crudo de yacimiento y nitrógeno. Se realizaron dos corridas a condiciones de laboratorio y una a condiciones de yacimiento. Los resultados experimentales fueron comparados por los predichos usando 16 modelos matemáticos. En el caso de permeabilidad relativa al aceite tres fases, las mejores correlaciones entre los datos experimentales y los predichos por los modelos de Blunt, Hustad Hasen, Baker se obtuvieron a saturaciones de aceite entre el 40% y 70%.

Palabras clave: yacimientos petrolíferos, estado no estacionario, flujo multifásico, permeabilidad relativa.

INTRODUCTION

Three-phase flow in petroleum reservoirs occurs when the water saturation is higher than the irreducible value and, in addition, oil and gas are present as mobile phases. Detailed predictions on petroleum reservoir behavior under recovery processes such as carbon dioxide injection, in-situ combustion, vapor injection, miscellaneous fluid injection, and nitrogen injection require three-phase relative permeability data. Three-phase relative permeability data have been rarely used in the past decades for the calculation of conventional reservoir engineering. Consequently, there is less knowledge about threephase relative permeability characteristics than that for two-phase relative permeability. The three-phase relative permeability is helpful in the estimation of reservoir behavior for oil fields whose production is based on the simultaneous flow of water and gas, or for reservoirs whose production are based on gas in solution which are partially depleted or those that produced by water drive, either aquifer-based or secondary-recovery based.

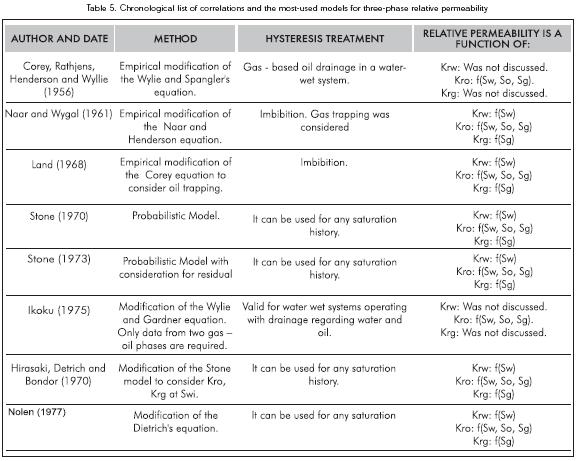
Analytical and numerical mathematical models are used in the petroleum industry to estimate threephase relative permeability from two-phase relative permeability data. Some of the most used models are: Corey, Rathjens, Henderson, and Wyllie (1956); Naar and Wygal (1961); Land (1968); Stone (1970); Stone (1973); Aziz and Settari (1973); Fayers and Mathews (1984). The main probabilistic models used in simulators are Stone (1970); Stone (1973); also some statistical approximations are used in these models and curve sets of two-phase (water-oil and oil-gas) relative permeability are employed. Oil relative permeability is estimated from these two-phase models to find a threephase system. The above mentioned models estimate relative permeability is based on the assumption that "each fluid establishes its own intricate path which, in turn, forms very stable flow channels".

BACKGROUND

Saraf and McCaffery (1981) published a complete study about the methods used in the determination of two-phase and three-phase relative permeabilities. As reported for the two-phase relative permeability, experimental three-phase relative permeability measurements are better than the values determined on a theoretical basis due to the many variables affecting three phase flow.

A summary of publications regarding three phase relative permeability are presented as follows.

Three-phase flow experiments in a steady state

In the steady state-method the wetting phase (typically water), the non-wetting phase (gas) and the intermediate phase (typically oil) are usually injected simultaneously in to the core. Pressure drop and saturation are measured when the system reaches the steady state, that is, when the pressure drops across the core and saturation does not change overtime (fluid distribution in a porous medium), as it occurs in the input and output fluids. The pressure drops through the core, as well as flow rates and fluid viscosities are replaced in the Darcy's Law to calculate effective permeabilities. Phase saturations are then modified by changing the ratio of the flow ratios. So that, the relative permeability curves can be obtained for a representative range of saturations.

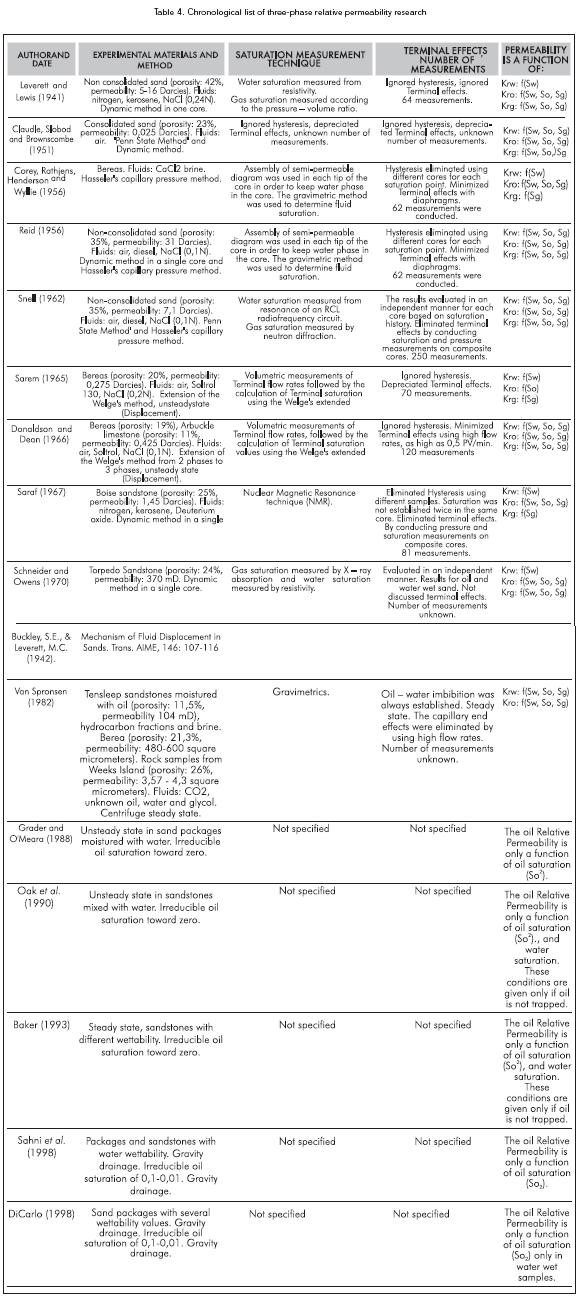
The first three- phase flow experimental study in the steady state was conducted by Buckley and Leverett (1942), who conducted their experiments in unconsolidated sand. Due to the inherent laboratory difficulties, only a few experimental studies for the determination of the three-phase relative permeabilities in steady state have been reported in the literature until 1990's. (Caudle, Slobod & Brownscomb, 1951; Corey, Rathjens, Henderson, & Wyllie, 1956; Reid, 1956; Snell, 1962; Saraf & Fatt, 1967; Schneider & Owens, 1970; Oak, 1990).

The experiments conducted by Oak (1991); Baker (1993) and Jerauld (1997) reported as from the 1990's onwards utilize the availability of more technological tools such as image scanning, measurement of fluid saturation through acoustic separators (Figure 4).

A common observation made by all these researchers is that the three phase relative permeability to the wetting phase is essentially a function of its own saturation and it is almost identical to wetting phase relative permeability obtained in a two-phase flow. On the other hand, relative permeabilities related to the nonwetting and intermediate phases vary according to the three-phase saturations. Most of the isoperms for the intermediate phase deviate from straight lines.

In the works above, the interpretation of relative permeability at steady state is based on the minimization of the end effects in order to obtain uniform saturation and then, apply directly the Darcy's Law extension to the multi-phase flow.

Three-phase flow experiment in unsteady state

In these experiments, one of the phases is injected into the core at a time. The core is at the irreducible saturation of the displacing phase. The fractional recovery and the pressure drop across the core are recorded continuously during the displacement process. Relative permeabilities are calculated by several methods. The most used are the Welge (1952), Johnson, Bossler, and Neumann method (1959) that is known worldwide as the JBN method. Sometimes history-matching based techniques are also used.

Lack of quantitative experiments for validation of the displacement theory delayed the reporting of relative permeabilities in a unsteady state until the publication of the works by Sarem (1966), Donaldson and Dean (1966), Saraf, Batycky, Jackson, and Fisher (1982) and Van Spronsen (1982). Grader & O'Meara Jr., (1988) successfully extended the Buckley-Leverett theory (Welge, 1952) for use in three phase unsteady state experiments and Siddiqui (1996), using X-ray CT-scanning technology for saturation determination, verified its validity under dynamic gas and dynamic water injections condictions.

At present, most of the three-phase relative permeability studies in a unsteady state take place by conducting displacement experiments, which normally involve in situ saturation measurements, (Skauge, Eleri, Graue, Monstad,1994; Skauge, Eleri, Graue, Monstad, 1995; Goodyear & Jones, 1995; Naylor, Sargent, Crosbie, Tlsed, Goodyear,1995; Hicks & Grader, 1996; Nordtvedt, 1997; Siddiqui, 1998; Di Carlo, Sahni & Blunt, 1998; Di Carlo, Sahni & Blunt, 2000).

Attached 1 shows a summary of some of the three-phase relative permeability experiments works. Mathematical models (both analytical and numerical) are used in the petroleum industry to estimate threephase relative permeability from two-phase relative permeability data. The oil relative-permeability values when oil saturation is high (greater than 50%) can generally be predicted by numerical and analytical methods. Some of the most commonly used models are: Corey et al. (1956); Naar and Wygal (1961); Land (1968); Stone (1970); Stone (1973); Aziz and Settari, Fayers ans Matthews, Neumann (1984). Attached 2 shows comparisons among the different methods and available correlations to evaluate three-phase relative permeabilities.

The main probabilistic models used in the numerical reservoir simulators are Stone I (1970) and Stone II (1973), which use statistical approximations. They also use oil-water and oil-gas relative permeability curves. The above mentioned models estimate relative permeability to the oil phase in a three-phase system from two-phase flow data based on the assumption that "each fluid establishes its own intricate path which, in turn, forms very stable flow channels" (Bear, 1972).

Each model assumptions can lead to optimistic or pessimistic oil relative permeability predictions. Figure 1 shows that with everything else being equal, the three models (Stone, Stone & Baker) can give three recovery efficiencies for the WAG process studied (Juanes & Spiteri, 2004).

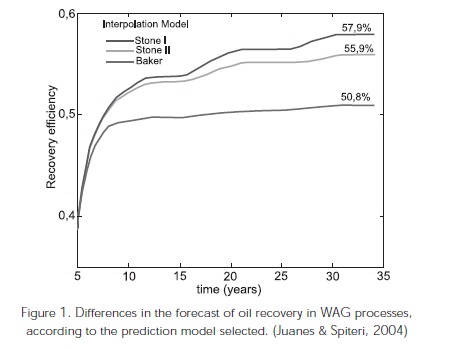
These models assume that relative permeabilities to gas and water depend on their respective saturations within the porous medium. However, the following phenomena have been observed in the laboratory, for which some of the assumptions used in the models may be violated.

• Hysteresis effects (dependence on saturation according to the different flow processes: drainage and imbibition) in relation to gas relative permeability.

• Presence of gas trapped in the porous medium.

• Displacement of the oil trapped (sor) by the gas phase.

• Critical oil saturation to initiate a three-phase flow, which can be different from the saturation found in two-phase runs.

• Effects of rock wettability on the form of the relative permeability curves.

• Reduction of water relative permeability in the presence of trapped gas (gas blockage).

• Negligible capillary pressures, incompressible fluids, uniform saturation profiles.

All the above mentioned phenomena cannot be reproduced by the numerical and analytical models and invalidate some assumptions given by the three-phase relative permeability models (Figure 2).

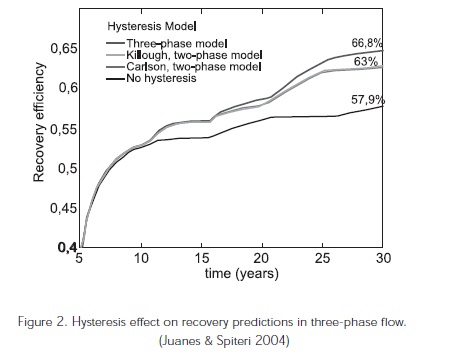
EXPERIMENTAL EQUIPMENT

Figure 3 shows a displacement equipment scheme that was modified at ICP for the conduction of threephase relative permeability tests. The equipment consists of a pumping system, a three-phase acoustic separator and a core holder with Bakelite isolators for resistivity measurements.

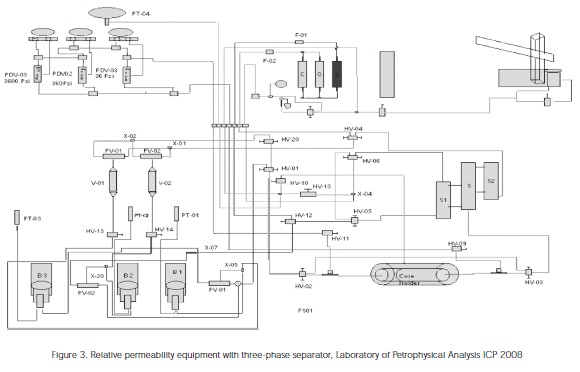
The pumping system consists of a closed loop recirculation system for two fluids: water and hydrocarbon. This system pumps the fluids into the sample at reservoir conditions. The water recirculation system consists of the Cylinder (S) and two Quizixs pumps B1 and B2. The cylinder initially feeds the two Quizx pumps. One of the Quizxis pump deliverys the brine while the other receives it from the sample or the separator. The working pump starts receiving water either from the output of the coreholder (in the case of the separator bypass) or from the three-phase separator.

The oil recirculation system is composed by the cylinders V-01 and V-02. While one cylinder sends the fluid into the sample, another receives the fluid returning from the separator. The cylinder receiving fluid is ready to send fluid to the sample before the other cylinder gets empty. The run of these two cylinders and their synchronization are controlled by the Pumpworks software and pumps B1 and B2.

All rates and pressures are continuously adjusted so the Switch between the cylinders occurs smoothly. A third pump (B3) acts as a backpressure regulators and works under a constant pressure mode (Servo Model).

The three-fluid storage cylinders (C, O, S) are placed out of the oven and complete a closed two-phase recirculation loop (water and hydrocarbon) at reservoir conditions.

Regarding the gas injection system, the cylinder C is conneted to an ISCO pump which allows gas injection into the core sample, passing through the separator where the recovered fluid is quantified, to exit finally to a backpressure system.

The fourth pump is located outside the oven. It is used to a maintain constant overburden pressure on the sample. A computer equipped with the Pumpworks software monitors the three phase relative permeability equipment and records data on differential pressure and interface level in the three-phase separator.

Figure 4 illustrates a schematic of the three-phase separator. Three cylinders (bores) are connected one another and fluids from the core sample enter through the top of the middle cylinder where separation occurs. The two measuring cylinders are connected to the separation cylinder. Volumes of each phase in the separator is obtained through the use of acoustic transducers that determine the distance from the transducer to the interface formed by the inmiscible fluid in the tube. Water and gas volumes can be determined accurately from these measurements. The oil volume is determined by subtracting the gas and water volumes from the total volume of the separator. Besides the pumping system, the three-phase acoustic separator and the Bakelite isolators coreholder for resistivity measures, there are also three cylinders located outside the oven (C, O, S) that are mentioned above for the storage of fluids

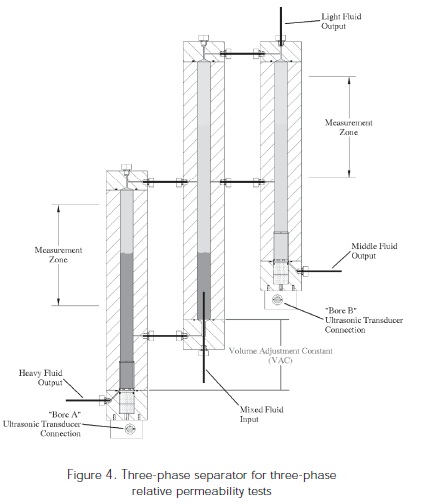
The specifications of the displacement equipment are as follows:

• Isothermal conditions up to 280°F (137,77 °C / 410,92 K).

• Confining pressure applied in a hydrostatic manner.

• Oven temperature tolerance : +/- 0,5°C (273,65 K).

• Wet gas is used.

PROTOCOL FOR THE MEASUREMENT OF THREE-PHASE RELATIVE PERMEABILITY, AT THE ICP PETROPHYSICAL ANALYSIS LABORATORY

The following paragraphs describe the unsteady- state methodology proposed for the evaluation of three-phase relative permeabilities. The methodology is based on the publications of Siddiqui and Yang, (1998), Nordtvedt (1997); Muhhammad and Muqeem (1994). The procedures proposed in these references were adapted according to the three-phase separator permeameter at the Petrophysical Laboratory.

Siddiqui and Yang (1998) used the three phase extension of the Buckley-Leverett theory and the Welge and JBN methods (Grader and O'Meara, 1988), to estimate saturation and relative permeabilities of the three phases, respectively. The experimental procedure consists of the initial establishment of a two-phase saturation condition (water and oil) within the core, using an unsteady state method (non-stationary) or a steady-state method (stationary), after which the dynamic injection of the third phase takes place. Recovery of each phase and the differential pressure are recorded during the test (water, oil, and gas). Saturations can be calculated using the data from the three-phase separators, or from resistivity measurements, and from the following Equation 1:

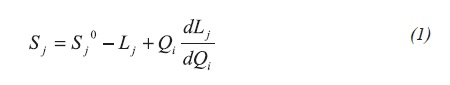
From Equation 1, saturation of the j-th phase can be calculated as a function of the initial saturation of the same phase before dynamic injection, S_j^o, considering the pore volumes of the injected gas Q_i, the pore volume of the produced phase j represented by L_j, and the slope of the recovery curve for each phase.

The relative permeabilities of each phase in the Equation 2.

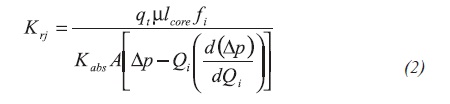
qt: production rate phase i, cc/min
M: Fluid viscosity, Cp.
Lcore: core length (cm)
Kabs: absolute permeability, md
A: area, cm
Delta p: pressure diferentia, psi

Where ƒ_i is the fractional flow of the i-th phase.

It is necessary to complete the following graphs shown in the Figure 5 and 6 in order to calculate saturations and relative permeabilities from the Equations 1 and 2, respectively. The objective is to calculate the slopes of the recovery curves and the differential pressure curves, respectively.

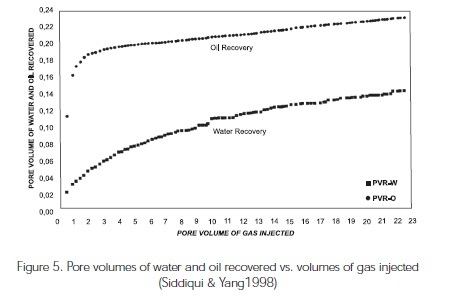
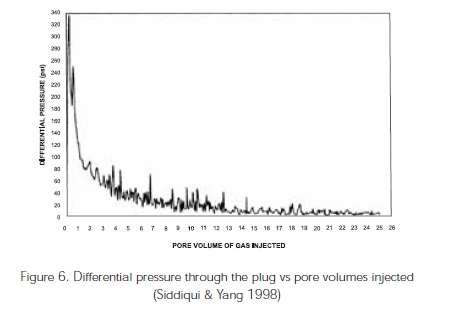
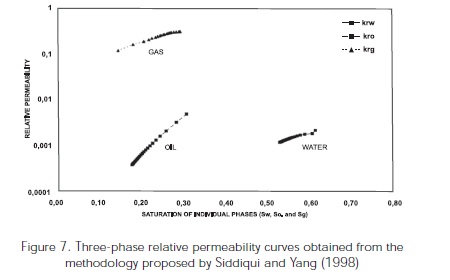
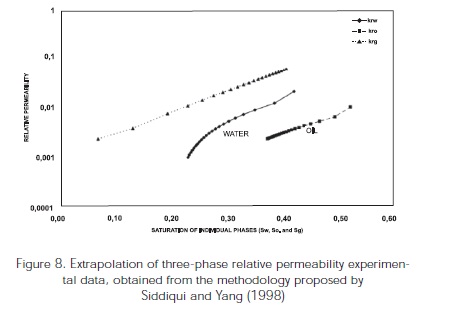
Siddiqui and Yang (1998) showed how relative permeabilities obtained can be extrapolated from the full saturation range (from critical saturation to maximum saturation) to obtain the complete curves shown in Figure 8.

The following steps are the protocol of the unsteady state test used in the laboratory tests conducted during the development of this work (samples A and 16054,92' of the Colombian foothills).

Vacuum saturation of the core sample using synthetic brine.

Calculation of brine absolute permeability at three rates. The operation conditions are:

- Temperature: ambient
- Overburden pressure: 800 psi
- Backpressure: 300 psi.
- Rates : 1; 1,5; 2 cm3/min.

Injection of mineral or crude oil in order to take the sample to the Swirr level (Irreducible water saturation).

Conduct waterflooding to calculate two-phase (wateroil) relative permeabilities (in order to calculate threephase relative permeabilities from correlations).

Displacement of oil and take the sample to the Swirr level again.

Establishment of the desired two-phase saturation (water and oil) within the core for each sample. To accomplish that, waterflooding (water injection) is initiated at a low rate (0,5 cm³/min) and continue monitoring oil input to the separator. Stop water injection when the desired water saturation is reached according to the volumetric balance.

For the sample A case, a water saturation of 53,3% and an oil saturation of 46,7% was established. Similarly for the sample 16054,92' a two-phase water saturation of 21,35% and an oil saturation of 78,65% was established.

Conduction of dynamic injection or unsteady state gas injection by adjusting the rate (2 cm³/min to 10 cm³/min) in order to obtain pressure stable differential across the core. Gas injection is stopped when stability in the pressure differential is reached as well as in the water-oil and gas-oil interfaces of the three-phase separator.

During the test run, recovery of each phase is recorded (water, oil and gas) as well as the differential pressure. The three-phase production is obtained directly through the interface readings in the three-phase separator. In addition, the Equation 1 is used for checking the three-phase separator results. Relative permeability of each phase is calculated from the Equation 2. Graphs similar to the ones shown in Figure 5 and 6 are necessary in this case.

Displacement by oil and take the sample to the Swirr level, Sgr (residual gas saturation).

Conduction of gasflooding (gas injection) to calculate two-phase gas-oil relative permeabilities (in order to calculate three-phase relative permeabilities from correlations).

After finishing gasflooding, the rock sample or plug is cleaned/extracted with the Dean Stark apparatus in order to determine the final saturation of water, oil, and gas.

RESULTS

In this section we show results of the experimental runs of three-phase relative permeability, unsteady state (non-stationary) conducted at room temperature using sample A and in the 16054,92' sample of the Colombian Foothills belonging to El Mirador formation. These runs had the purpose of validating the un-steady state methodology, proposed during the development of this work.

In the runs conducted at room temperature using the three-phase relative permeability setup, the injection fluids were NaCl brine of 37,000 ppm (viscosity: 1 cp), mineral oil (viscosity: 58 cp) and Nitrogen (viscosity: 0,017 cp). In the run conducted at reservoir temperature, the injection fluids were NaCl brine 37,000 ppm (viscosity: 0,24 cp), light crude oil (viscosity 2,4 cp) and Nitrogen. A recipient for humidifying nitrogen was installed in the displacement equipment before passing it through the core sample.

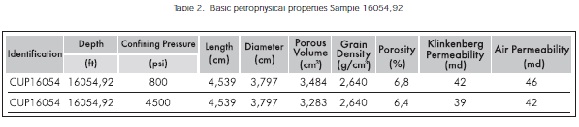
Before the initiation of the test, determination of porosity and permeability for the samples A and 16054,92' from the Colombian Foothills were conducted at the ICP Basic Petrophysical Laboratory. The basic petrophysical properties (routine properties) obtained for sample A were:

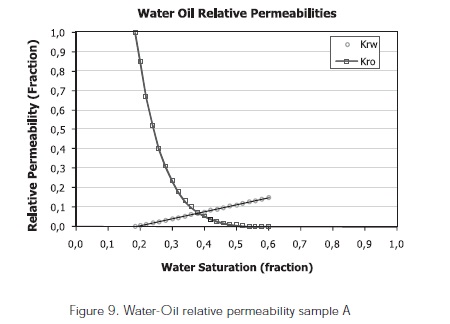
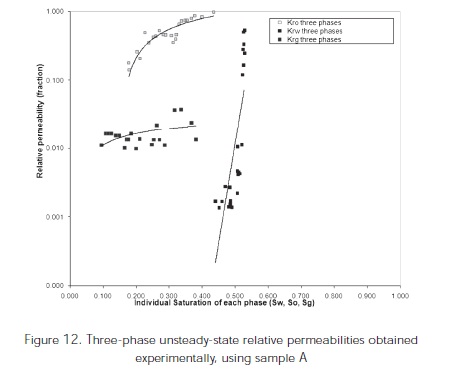
Figure 9, 10, 12 show permeability curves for water-oil, gas-oil and three-phase permeability for sample A. The water-oil relative permeability analysis of sample A at laboratory conditions (Figure 9) represents an irreducible saturation of water of 18,7% and an oil residual saturation of 40%. After conducting the water-oil relative permeability, sample A was saturated with mineral oil and then water was displaced to the sample during one hour at a rate of 1 cm³/min. A final water saturation in the sample of 53% and an oil final oil saturation of 47% were obtained according to the separator readings. During the three-phase relative permeability test, nitrogen injection was conducted at a rate of 10 cm³/min during two hours approximately. Upon completion of the experiment, a water final saturation of 44%, an oil saturation of 18% and a gas saturation of 38% were obtained. Upon finishing the three-phase relative permeability test, the sample was re-saturated with mineral oil and nitrogen was again injected to find the gas-oil relative permeability (Figure 10).

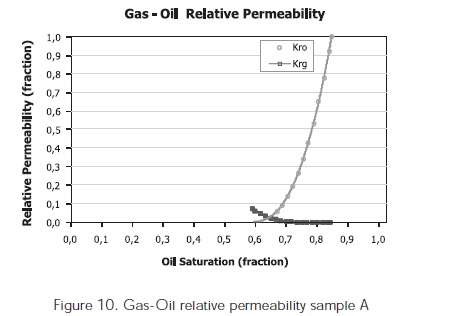
The residual saturation value of oil obtained with the gas flooding was 41%, and the gas relative permeability was 0,075.

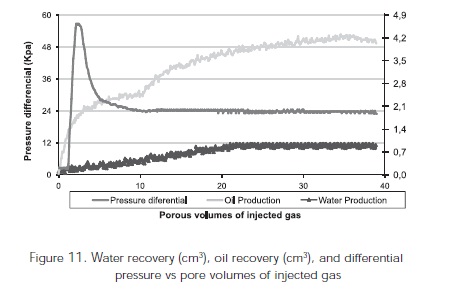
Figure 11 shows water and oil recovery (cm³) as well as the pressure differential vs. injected gas porous volumes. With the water-oil and gas-oil relative permeability data shown in Figures 9 and 10, the three-phase relative permeabilities were calculated using the 16 available correlations for the calculation of three-phase relative permeabilities. Correlations were programmed using Excel.

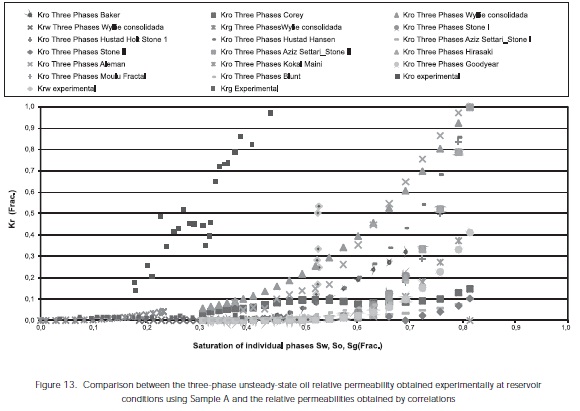
Figure 13 shows a comparison between the threephase relative permeabilities obtained through unsteady state experiments using sample A and those obtained from correlations.

For the 16054,92' sample from the Colombian Foothills belonging to El Mirador formation, the same experimental procedure and the same injection fluids at sample A were used. Figures 14, 15, and 17 show the water-oil, gas-oil and three-phase relative permeabilities for the sample 16054,92'. The water-oil relative permeability analysis for the 16054,92' sample at the laboratory condition (Figure 14) shows an irreducible water saturation of 10,37% and an oil residual saturation of 24,9%. After conducting the water-oil relative permeability, the 16054,92' sample was re-saturated with mineral oil and then water was displaced to the sample for 30 minutes at a rate of 1 cm³/min. a water saturation value of 23,5% and an oil saturation value of 78,65% were obtained according to the separator readings. During the three-phase relative permeability test, nitrogen injection was conducted at a rate of 5 cm³/min for 2 hours approximately. Upon completion of the experiment, a final water saturation of 15,9%, an oil saturation of 41,65% and a gas saturation of 42,45%. Upon completion of the three-phase relative permeability test, the sample was restored with mineral oil and nitrogen was injected again to conduct the gas-oil relative permeability test (Figure 15). The residual oil saturation obtained with gas flooding was 40,2%, and the gas relative permeability was 0,092.

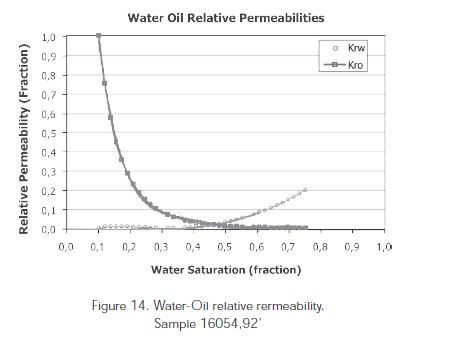
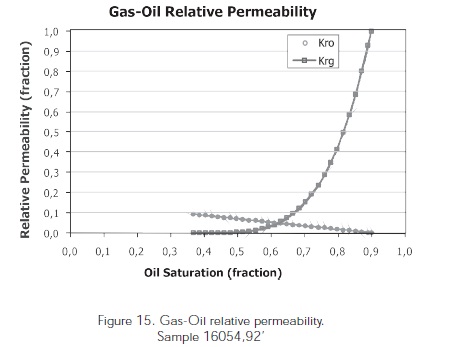
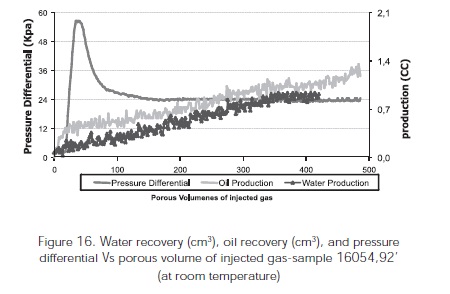
Figure 16 shows the recovery plots for water and oil recoveries (cm³) as well as pressure differential vs. pore volumes of injected gases. The second hump seen in the oil recovery data (Figures 11 and 16) may be linked with some oil bank generation.

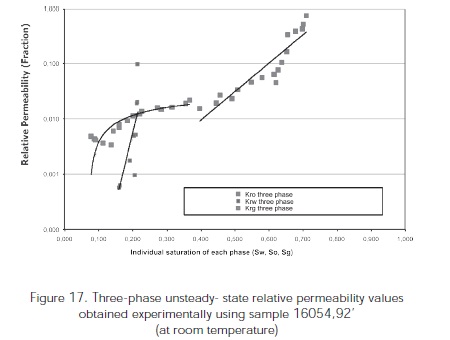
With the water-oil and gas-oil Relative Permeability data shown in Figures 14 and 15 the three-phase relative permeability values were calculated using 16 correlations available for the calculation of the three-phase relative permeability values. Correlations were programmed using Excel.

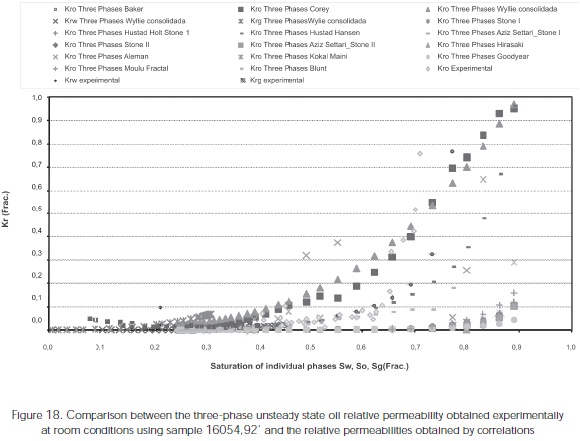
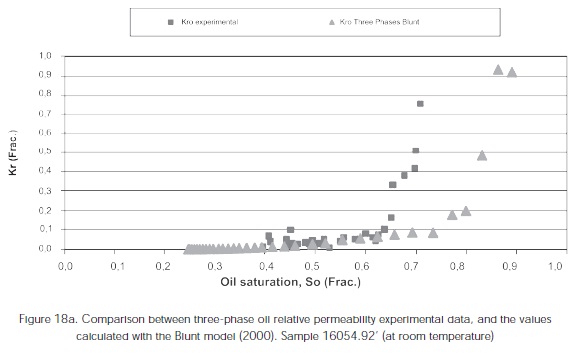
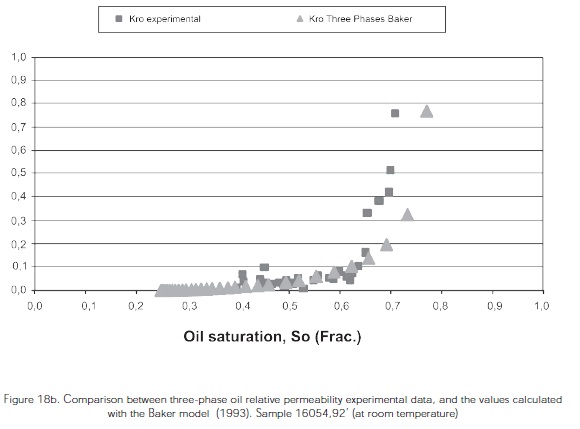
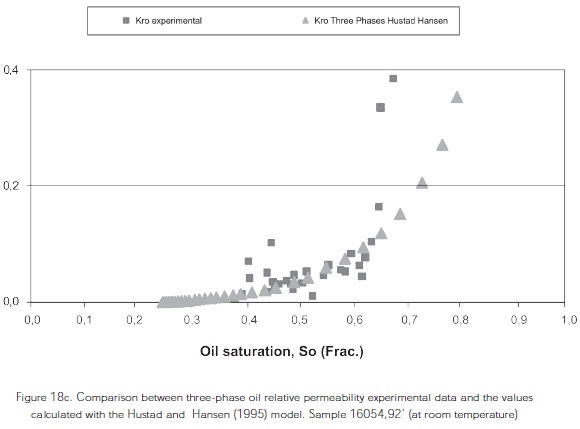
Figure 18 shows the comparison between the threephase relative unsteady-state relative permeabilities obtained experimentally under laboratory conditions in the 16054,92' sample, and the permeabilities obtained by correlations.

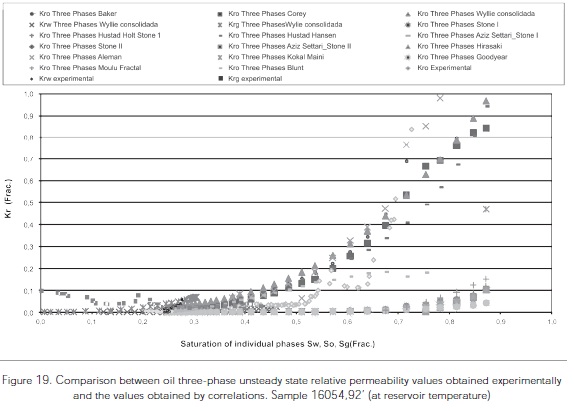
After finishing the 16054,92' sample run under laboratory conditions, the sample was cleaned and the test was repeated at reservoir conditions using the same procedure but with a crude oil instead of the mineral oil. The wateroil relative permeability analysis for the sample 16054,92' at reservoir conditions exhibits an irreducible water saturation of 12,7% and an oil residual saturation of 24,7%. After conducting the water-oil relative permeability test, the sample 16054,92' was re-saturated with crude oil and then water was flowed through to the sample for fifteen minutes at the rate of 1cm³/min. According to the separator readings, a water saturation value of 27,09% and an oil saturation value of 72,91% were obtained. During the three-phase relative permeability stage, nitrogen was injected at the rate of 2 cm³/min for approximately 7 hours. A final water saturation of 16,8%, an oil saturation of 35,87% and a gas saturation of 47,37% were obtained at the end of the experiment. Figure 19 shows the comparison between experimental results at reservoir conditions and the results predicted based on mathematical models (correlations).

The Basic petrophysical properties corresponding to the sample 16054,92' were obtained before the initiation of the test run at the ICP laboratory of basic petrophysical properties. These are:

Figures 18a, 18b, 18c show the correlation betwen experimental data and data predictions from the Blunt (2000); Hustad and Hansen (1995); Baker (1993) models at oil saturation values between 40% and 69% for the sample 16054,92'

DISCUSSION OF RESULTS

In order to quantify the effectiveness of each model to predict the three-phase oil relative permeability data, the sum of the deviation squared between experimental data and calculated values was used. The deviation was calculated using the following Equation 3:

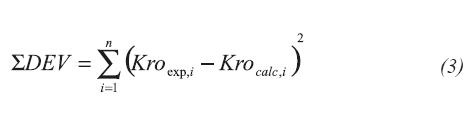
Figures 13, 18, and 19 show the comparison of K_ro experimental data (oil relative permeability), K_rw (water relative permeability) and K_rg (gas relative permeability) three phases (at laboratory conditions) for sample A and the sample 16054,92' from the Colombian Foothills (at laboratory and reservoir conditions). The following observations were made based on this comparison:

• The only correlation that allows the calculation of three-phase K_rw and three-phase K_rg is the consolidated Wyllie correlation. However, in the sample A case and the sample 16054,92' from the Colombian Foothills consolidated Wyllie correlations over predict both K_rw and K_rg.

• For the three - phase K_ro of Sample A, all correlations compared to the experimental data under predicted the three-phase K_ro. The main reason for this difference could be because the three-phase relative permeability test was initiated at an oil saturation less than 50%.

• For the three-phase K_ro for the sample 16054,92' from Colombian Foothills at both laboratory and reservoir conditions the Pope, the consolidated Wyllie, the Corey, and the Aleman, correlations over predicted the three-phase K_ro.

• For the three-phase K_ro of the sample 16054,92' from the Colombian Foothills at laboratory and reservoir conditions, the correlations of Aziz and Settari (Stone modified), Kokal and Maini, Stone I, Stone II, Aziz and Settari (Stone I modified), Hustad & Hold (Stone I modified), Hirasakí, Goodyear- Townsley, and Moulu (Fractal) under predicted three- phase K_ro.

• For the three-phase K_ro of the sample 16054,92' from the Colombian Foothills at both laboratory and reservoir conditions, a good correlation was observed between the experimental data and the data predicted by the Blunt, Hustad and Hansen, and the Baker correlations at oil saturation between 40% and 69%. The following table shows the deviation obtained for these models.

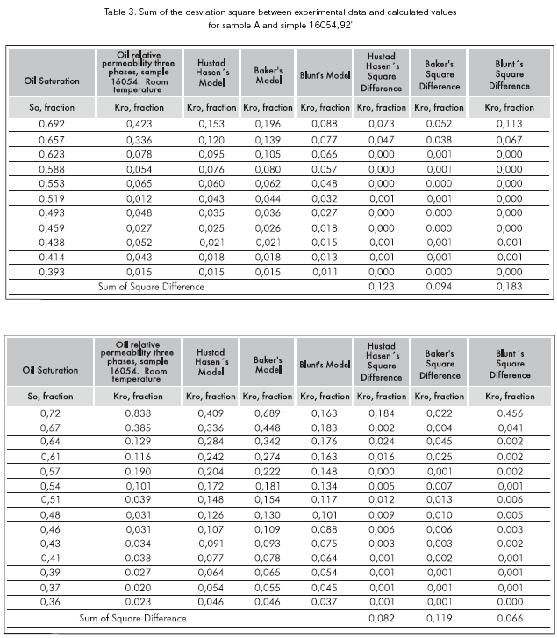
• It is observed in the results obtained in the three runs conducted (Sample A and sample 16054,92'), that the three-phase oil relative permeability calculated using mathematical models shows good agreement with the three-phase oil relative permeability obtained experimentally only at high oil saturations (40-70%).

CONCLUSIONS

• The laboratory tests conducted on Sample A and in the sample 16054,92' from the Colombian Foothills, report that the comparison between the three-phase oil relative permeability obtained by experimental means and the permeability obtained from analytical models do not always show good agreement at all oil saturations ranges, between critical saturations and maximum saturations. The best correlation between the oil relative permeability measured by experimental means and the oil relative permeability obtained from correlations were obtained for the oil saturation range between 40% and 70%.

• Regarding water relative permeability and the threephase gas permeability, the consolidated Wyllie correlation was the only correlation available to compare with the data obtained experimentally. It is observed, in both cases, that the Wyllie's correlation over predicts the relative permeability for the analyzed samples (sample A and 16054,92').

• Review of experimental data corresponding to the three-phase relative permeability, and available models in the literature indicate that there are still problems remaining to be solved. From the experimental standpoint, the main problem is to obtain good quality saturation and relative permeability data. From the analytical and numerical standpoint, the main problem is to incorporate physical phenomena occurring in the porous media, such as the effect of the interfacial tension, history of fluid saturation, kinetic effects such as drop coalescence and pore geometry. These facts can also lead to either optimistic or pessimistic oil relative permeability predictions. The fluid injectivity calculation and oil recovery predicted in a reservoir simulation, is affected in the well depending on the model selected.

ACKNOWLEDGMENTS

The authors would like to express their feelings of gratitude to the personnel at the ICP Basic and Special Petrophysics Laboratory, especially to the technologist Diego A. Corzo and engineer Jorge A. Rojas for their support in the correct development of the laboratory tests.

REFERENCES

Aziz, K., & Settari, A. (1973). Petroleum Reservoir Simulation. London: Applied Science Publishers.        [ Links ]

Baker, L .E. (1993). Three-Phase Relative Permeability of Water-Wet, Intermediate-Wet, and Oil-Wet Sandstone. Seventh European Improved Oil Recovery Symposium, Moscow, Russia.        [ Links ]

Bear, J. (1972). Dynamics of Fluids in Porous Media. Environmental Science Series, Elsevier, New York.        [ Links ]

Blunt, M. J. (2000). An Empirical Model for Three-Phase Relative Permeability. Soc. Pet. Eng. J., 5 (4), 435-445.        [ Links ]

Buckley, S. E., & Leverett, M. C. (1942). Mechanism of Fluid Displacement in Sands. Trans. AIME, 146: 107-116.        [ Links ]

Caudle, B. H., Slobod, R.L., & Brownscomb, E. R. (1951). Further Developments in the Laboratory Determination of Relative Permeability. Trans. AIME, 192: 145-150.        [ Links ]

Corey, A., Rathjens, C., Henderson, J., & Wyllie, M. (1956). Three-Phase Relative Permeability. Petrol. Trans. AIME, 207: 349-351.        [ Links ]

DiCarlo, D. A., Sahni, A., & Blunt, M. J. (2000). The Effect of Wettability on Three-Phase Relative Permeability. Transp. Porous Media, 39: 347-366.        [ Links ]

Dickey, P. A., & Bossler, R. B. (1944). Role of Connate Water in Secondary Recovery of Oil. Petrol. Trans. AIME, 155: 175-183.        [ Links ]

Donaldson, E. L., & Dean, G. W. (1966). Two - and Three- Phase Relative Permeability Studies. Technical Report RI 6826, US Bureau of Mines.        [ Links ]

Eleri, O. O., Skauge, A., & Graue, A. (1995). Steady State and Unsteady State Two-Phase Relative Permeability Hysteresis and Measurements of Three-Phase Relative Permeability Using Imaging Techniques., SPE Ann. Tech. Conf. and Exhibition, Dallas, TX. SPE 30764        [ Links ]

Fayers, F. J., & Matthews, J. D. (1984). Evaluation of Normalized Stone's Methods for Estimating Three- Phase Relative Permeabilities. Soc. Pet. Eng. J. 24 (2), 224-232.        [ Links ]

Goodyear, S. G., & Jones, P. I. R. (1995). Relative Permeabilities for Gravity Stabilized Gas Injection. Eight European Improved Oil Recovery Symposium, Vienna, Austria.        [ Links ]

Grader, A. S., & O'Meara Jr., D. J. (1988). Dynamic Displacement Measurements of Three-Phase Relative Permeabilities Using Three Immiscible Fluids. SPE Ann. Tech. Conf. and Exhibition, Houston, TX. SPE 18293.        [ Links ]

Hicks Jr., P. J., & Grader, A. S. (1996). Simulation of Three-Phase Displacement Experiments. Transp. Porous Media, 24: 221-245.        [ Links ]

Holmgren, C. R. (1949). Some Results of Gas and Water Drives on a Long Core. Petrol. Trans. AIME, 179: 103-118.        [ Links ]

Holmgren, C. R., & Morse, R. A. (1951). Effect of Free Gas Saturation on Oil Recovery by Waterflooding. Petrol. Trans. AIME, 192: 135-140.        [ Links ]

Hustad, O. S., & Hansen A. G. (1995). A consistent correlation for three phase relative permeabilities and phase pressures based on three sets of two phase data. 8^th EAPG Impr. Oil Recovery European Symposium, Vienna, 1: 289.        [ Links ]

Jerauld, G. R. (1997). General Three-Phase Relative Permeability Model for Prudhoe Bay. SPE Res. Eng.,12 (4), 255-263.        [ Links ]

Johnson, E. F., Bossler, D. P., & Neumann, V. O. (1959). Calculation of Relative Permeability from Displacement Experiments. Petrol. Trans. AIME, 216: 370-372.        [ Links ]

Jones, S. C., & Roszelle, W. O. (1978). Graphical Techniques for Determining Relative Permeability From Displacement Experiments. J. Petroleum Technol., May. 807-817.        [ Links ]

Juanes, R., & Spiteri, E. (2004). Impact of Relative Permeability Hysteresis on WAG Injection. SPE 89921.        [ Links ]

Land, C. S. (1968). Calculation of Imbibition Relative Permeability for Two- and Three-Phase Flow from Rock Properties. Soc. Pet. Eng. J., 8 (2), 149-156.        [ Links ]

Muqeem, M. A. (1994). Effect of temperature on three phase relative permeability. Ph. D. Thesis, Petroleum Engineering, University of Alberta, Canada.        [ Links ]

Naar, J., & Wygal, R. J. (1961). Three-Phase Imbibition Relative Permeability. Soc. Pet. Eng. J, 1 (4), 254-258.        [ Links ]

Naylor, P., Sargent, N. C., Crosbie, A. J., Tilsed, A. P., & Goodyear, S.G. (1995). Gravity Drainage During Gas Injection. Eight European Improved Oil Recovery Symposium, Vienna, Austria.        [ Links ]

Nortvedt, J. E., Ebeltoft, E., Iversen, J. E., Urkedal, H., Vatne, K. O., & Watson, A. T. (1997). Determination of Three-Phase Relative Permeabilities from Displacement Experiments. SPE Form. Eval., 12 (6), 221-226. SPE 36683.        [ Links ]

Oak, M. J. (1990). Three-Phase Relative Permeability of Water-Wet Berea., SPE/DOE Seventh Symposium on Enhanced Oil Recovery, Tulsa, OK. SPE/DOE 20183.        [ Links ]

Oak, M. J. (1991). Three-Phase Relative Permeability of Intermediate-Wet Berea Sandstone. SPE Ann. Tech. Conf. and Exhibition, Dallas, TX. SPE 22599.        [ Links ]

Reid, S. (1956). The Flow of Three Immiscible Fluids in Porous Media. Ph.D. Dissertation, University of Birmingham, U. K.        [ Links ]

Sahni, A., Burger, J. E. & Blunt, M. J. (1998). Measurement of Three-Phase Relative Permeability During Gravity Drainage Using CT Scanning., SPE/DOE Symposium on Improved Oil Recovery, Tulsa, OK. SPE 39655.        [ Links ]

Saraf, D. N., & Fatt, I. (1967). Three-Phase Relative Permeability Measurement Using a Nuclear Magnetic Resonance Technique for Estimating Fluid Saturation. Soc. Pet. Eng. J. 7 (3), 235-242.        [ Links ]

Saraf, D. N., & McCaffery, F. G. (1981). Two and Three Phase Relative Permeabilities: A Review. Petroleum Recovery Research Institute Report No. 81-8.        [ Links ]

Saraf, D. N., Batycky, J. P., Jackson, C. H., & Fisher, D. B. (1982). An Experimental Investigation of Three-Phase Flow of Water-Oil-Gas Mixtures through Water-Wet Sandstones. SPE, California Regional Meeting, San Francisco, CA. SPE 10761.        [ Links ]

Sarem, A. M. (1966). Three-Phase Relative Permeability Measurements by Unsteady-State Method. Soc. Pet. Eng. J., 6 (3), 199-205.        [ Links ]

Schneider, F. N., & Owens, W.W. (1970). Sandstone and Carbonate Two - and Three-Phase Relative Permeability Characteristics. Soc. Pet. Eng. J. 10 (1), 75-84.        [ Links ]

Siddiqui, S., Hicks, P. J., & Grader, A. S. (1996). Verification of Buckley Leverett Three Phase Theory Using Computerized Tomography, J. Pet. Sci. Eng. 15(1), 1-21.        [ Links ]

Siddiqui, S., Yang, J., & Ahmed, M. (1998). Dynamic Displacement Measurement of Three Phase Relative Permeabilities in Berea Sandstone Cores. SPE 49306.        [ Links ]

Skauge, A, Eleri, O. O., Graue, A., & Monstad, P. (1994). Influence of Connate Water on Oil Recovery by Gravity Drainage. SPE/DOE Ninth Symposium on Improved Oil Recovery, Tulsa, OK. SPE 27817.        [ Links ]

Snell, R.W. (1962). Three-Phase Relative Permeability in an Unconsolidated Sand. J. Inst. Pet. 48, 80-88.        [ Links ]

Van Spronsen, E. (1982). Three-Phase Relative Permeability Measurements Using the Centrifuge Method. SPE/DOE Third Symposium on Enhanced Oil Recovery, Tulsa, OK. SPE 10688.        [ Links ]

Stone, H. L. (1970). Probability Model for Estimation Three- Phase Relative Permeability. Journal of Petroleum Technology, 20, 214-218.        [ Links ]

Stone, H. L. (1973). Estimation of Three-Phase Relative Permeability and Residual Data, Journal of Canadian Petroleum Technology, 12, 53-61.        [ Links ]

Welge, H. J. (1949). Displacement of Oil from Porous Media by Water or Gas. Petrol. Trans. AIME, 179, 133-145.        [ Links ]

Welge, H. J. (1952). A Simplified Method for Computing Oil Recovery by Gas or Water Drive. Petrol. Trans. AIME, 195, 91-98.        [ Links ]