ABSTRACT

The analysis of injection tests under nonisothermic conditions is important for the accurate estimation of the reservoir permeability and the well's skin factor; since previously an isothermical system was assumed without taking into account a moving temperature front which expands with time plus the consequent changes in both viscosity and mobility between the cold and the hot zone of the reservoir which leads to unreliable estimation of the reservoir and well parameters.

To construct the solution an analytical approach presented by Boughrara and Peres (2007) was used. That solution was initially introduced for the calculation of the injection pressure in an isothermic system. It was later modified by Boughrara and Reynolds (2007) to consider a system with variable temperature in vertical wells. In this work, the pressure response was obtained by numerical solution of the anisothermical model using the Gauss Quadrature method to solve the integrals, and assuming that both injection and reservoir temperatures were kept constant during the injection process and the water saturation is uniform throughout the reservoir.

For interpretation purposes, a technique based upon the unique features of the pressure and pressure derivative curves were used without employing type-curve matching (TDS technique). The formulation was verified by its application to field and synthetic examples. As expected, increasing reservoir temperature causes a decrement in the mobility ratio, then estimation of reservoir permeability is some less accurate from the second radial flow, especially, as the mobility ratio increases.

Key words: permeability, radial flow, anisothermical flow, mobility, injection front.

RESUMEN

El análisis de pruebas de inyección en condiciones no isotérmicas es importante para la determinación correcta de la permeabilidad de la formación y el factor de daño del pozo, ya que anteriormente se asumía un sistema isotérmico, sin tener en cuenta un frente de temperatura que se expande con el tiempo con los consecuentes cambios de viscosidad y movilidad entre la zona fría y la zona caliente del yacimiento, incurriendo en la estimación de resultados no confiables de los parámetros del yacimiento y el pozo.

Para construir la solución se utilizó la aproximación analítica presentada inicialmente por Boughrara y Peres (2007) para el cálculo de la presión de inyección en un sistema isotérmico y, luego, modificada, por Boughrara y Reynolds (2007) para un sistema con temperatura variable en pozos verticales. La respuesta de presión se obtuvo mediante la solución numérica del modelo anisotérmico utilizando el método de Cuadratura Gaussiana en la resolución de integrales, teniendo en cuenta que las temperaturas de inyección y del yacimiento se mantienen constantes a lo largo del tiempo, y que la saturación de agua es uniforme a través del yacimiento.

Para efectos de interpretación se formuló una técnica basada en las características únicas halladas en la curva de presión y derivada de presión sin emplear curvas tipo (Técnica TDS). Se realizaron ejemplos sintéticos y de campo para efectos de verificación de la formulación presentada. Como era de esperarse, al aumentar la temperatura del yacimiento se reduce la relación de movilidades, lo que ocasiona un poco menos de exactitud al estimar la permeabilidad del segundo flujo radial.

Palabras Clave: permeabilidad, flujo radial, flujo anisotérmico, movilidad, frente de inyección.

INTRODUCTION

Heat transfer has to take place when there exist temperature differences inside a medium. When cold water is injected into a hot reservoir, the formation surrounding the well cools down to reach the level of the injected water temperature. The heat exchange in the reservoir mainly occurs by both convection between injected fluid and matrix, and conduction.

Platenkamp (1985) showed the importance of heat transfer when cold water is injected in a reservoir containing hot oil. He concluded that heat transfer by conduction is negligible compared to that by convection during an injection period as long as the test duration do not be so long and injection rate be sufficiently high.

In an injection test, the well is shut-in until the pressure reaches stabilization at the initial reservoir pressure. Then, injection starts at a rate, Q_inj, while the well-flowing pressure is recorded as time goes on. For an accurate injection test interpretation, the anisothermical effects of the moving thermal front and the distance to it has to be considered.

MATHEMATICAL MODEL

Dimensionless quantities

The dimensionless variables are defined in terms of oil properties at the irreducible water saturation, S_wi. The dimensionless variables are defined by Boughrara and Peres (2007) in Equation 1:

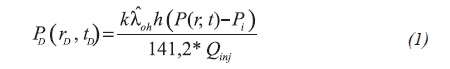
Where Equations 2, 3 and 4:

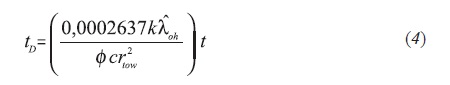
Where Equation 5:

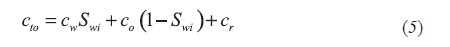
Radial flow solution

Boughrara and Reynolds (2007) provided a solution which considers constant rate injection, Q_inj, of cold water at a temperature T_wi in a vertical well drilled in a homogeneous reservoir with an initial temperature initial T_oi. It was also assumed that the initial saturation distribution is constant and equal to the irreducible water saturation, S_wi, and fluids viscosities are only a function of temperature. The temperature distribution can be approximated to:

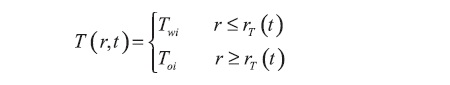
Where r_T(t) is the radial position of the temperature front which is calculated by an expression provided by Benson and Bodvarsson (1986) who studied the anisothermical effects and built a numerical model for the estimation of permeability and skin factor in injection tests, Equation 6:

Platenkamp (1985) derive an Equation to estimate the position of the moving front Equation 7:

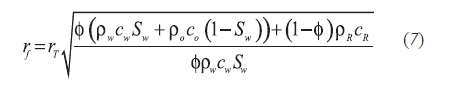
Using the assumption that both the water front and the temperature front fall inside a "steady state region" so that total rate is equal to injection rate, Q_inj, and following a procedure similar to the one presented by Boughrara and Reynolds (2007), a modified analytical solution for cold water injection in a hot oil reservoir drained by a vertical well is presented here as Equation 8:

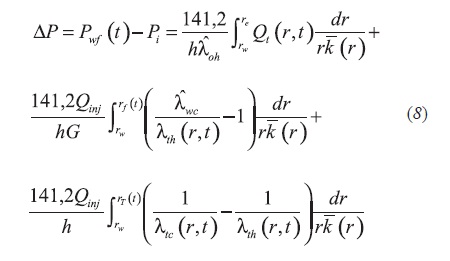
Where Equations 9, 10 and 11:

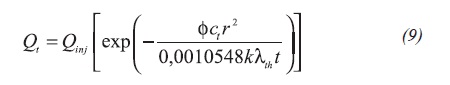
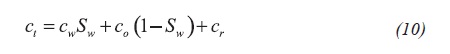
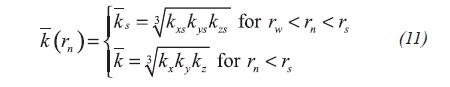
Due to the fact that the system is subjected to two different temperatures, λ_tc represents the total mobility estimated at T_wi, and valid for r < r_T, while λ_th represents the total mobility calculated at, T_oi, which is valid for r > r_T. These are defined by Equations 12 and 13:

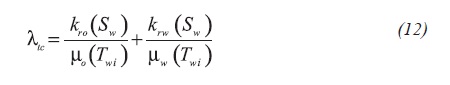
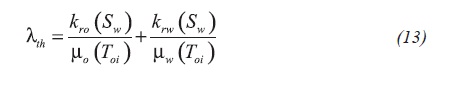
The end-point oil mobility evaluated at water injection temperature is defined as Equation 14:

Similarly, the terminal water mobility evaluated at T_oi and T_wi is given by Equations 15 and 16 :

Variable G introduced in this work depends upon the end-point mobility ratio. This term has been introduced in the second integral of the pressure transient model, Equation 8, to appropriately account for the temperature variations. It is defined as follows in Equations 17 and 18:

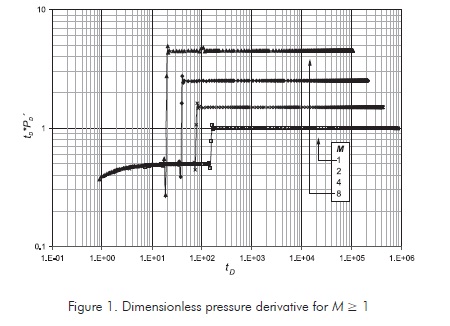
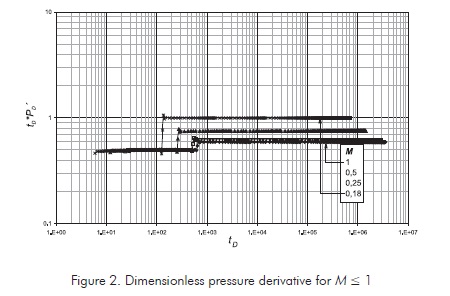
The pressure behavior obtained from the application of Equation 8 are reported in Figures 1 and 2. In both cases is observed that as the mobility ratio increases due to temperature effects the pressure derivative in the second plateau also increases its value and the moving front position gets closer. Notice in Figures 1 and 2 that as M is much larger than one, the first radial flow is shorter.

INTERPRETATION METHODOLOGY

The way the interpretation Equations are formulated follows the philosophy of the Tiab's Direct Synthesis Technique (TDS Technique), introduced by Tiab (1995). As observed in Figures 1 and 2, the pressure derivatives during the radial flow regimes are, respectively, given by Equations 19 and 20:

Alter plugging the dimensionless quantities in the above expressions, it yields, respectively in Equations 21 and 22:

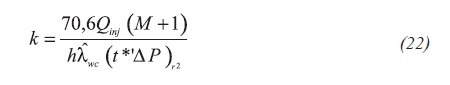
By analogy with the procedure presented by Tiab (1995), the skin factor formulae are Equations 23 and 24:

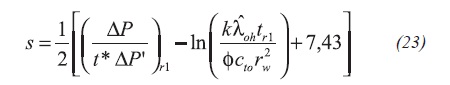
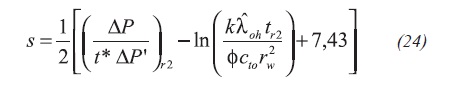
EXAMPLES

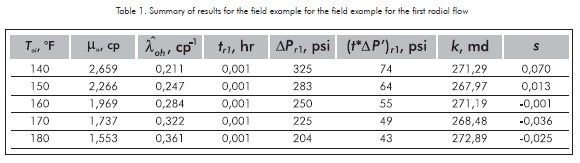
Field example

It is required to estimate permeability and skin factor from a field example provided by Boughrara and Reynolds (2007). Figure 3 presents the pressure and pressure derivative data for an injection test in a hot reservoir at a temperature of 180°F when µ_o(T_oi) = 1,553 cp. The following are some other relevant data:

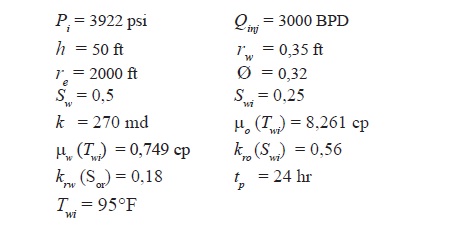
Solution

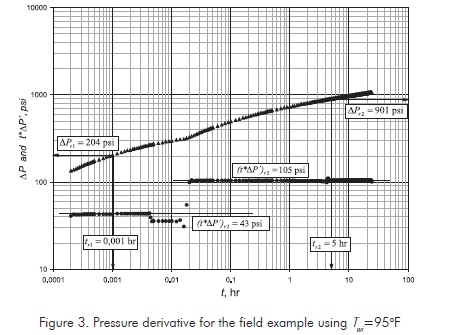
The following information is read from Figure 3:

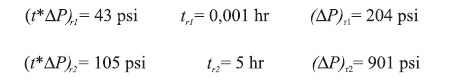
For the first radial flow, using Equations 14 and 21:

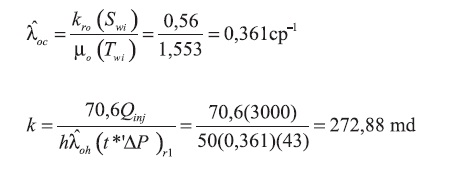
Skin factor is obtained from Equation 23:

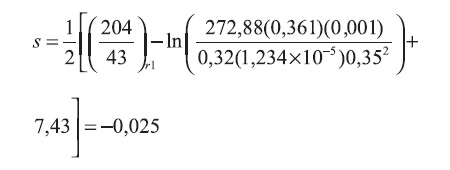
For the second radial flow, using Equations 15 and 22, it is obtained:

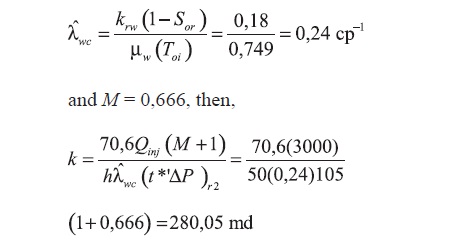
Skin factor is obtained from Equation 24:

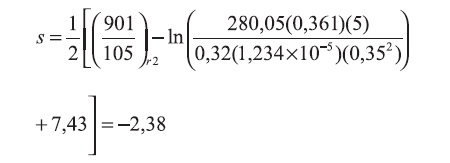
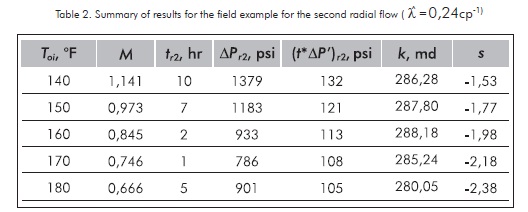
As we see permeability results agree with the value reported by Boughrara and Reynolds (2007). Simulation runs were also performed for other four temperatures. Although, the pressure and pressure derivative plots are not shown here, the results for these cases are reported in Tables 1 and 2.

Synthetic example

The pressure and pressure derivative shown in Figure 4 were simulated in this study with the information given below. Estimate reservoir permeability and skin factor for µ_o(T_oi) = 3,661 cp.

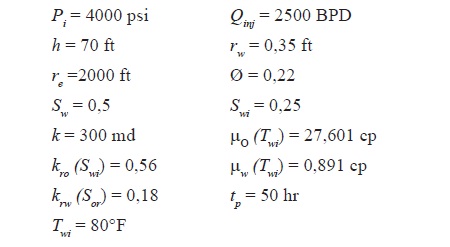
Solution

The following parameters are read from Figure 4:

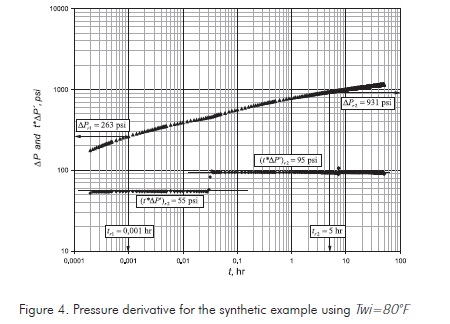
For the first radial flow, using Equation 14 and Equation 21, values of χ of 0,153 cp^-1 and a formation permeability of 299,64 md were obtained. The skin factor estimated with Equation 23 was of 0,198. For the second radial flow a value of χ = 0,202 cp-1 was estimated with Equation 15. Then, the mobility ratio, M, is equal to 1,32. Equation 22 allows us to estimate a reservoir permeability of 304,83 md and a skin factor of -1,56 is estimated with Equation Equation 24. Notice that the skin factor obtained from the second derivative implies a stimulation caused by the oil viscosity reduction.

CONCLUSIONS

• A new formulation to estimate permeability and skin factor in injection tests subjected to temperature variation from the pressure and pressure derivative plot using the TDS technique are presented and successfully tested.

• The second integral in the pressure transient model was modified to appropriately account for the temperature variations.

• From the pressure and pressure derivative plot, it is observed that increasing the reservoir temperature while keeping constant the injection temperature causes a reduction in the mobility ratio, injection pressure and pressure derivative, as well. A reduction of the mobility ratio causes a more significant change in pressure derivative when the distance from the well to the moving temperature front are much higher than the well radius.

• Estimation of reservoir permeability and skin factor is more accurate from the first radial flow. Accuracy from the second radial flow decreases as mobility ratio increases.

ACKNOWLEDGMENTS

The authors gratefully acknowledge the financial support of Universidad Surcolombiana for the completion of this study.

REFERENCES

Benson, S. M., & Bodvarsson, G. S. (1986). Nonisothermal Effects During Injection and Falloff Test. SPE Formation Evaluation, Feb. 1986: 53-63.        [ Links ]

Boughrara, A. A., & Reynolds, A. C. (2007). Practical Analysis of Injection / Falloff Data of Horizontal Wells. Paper SPE 109799, presented at the ATCE 2007 held in Anaheim, California, Nov. 11-14.        [ Links ]

Boughrara, A. A., & Peres, A. M. (2007). Approximate Analytical Solutions for the Pressure Response at a Water- Injection Well. J. Petroleum Scien. and Engineer., March 2007, 12 (1): 19-34.        [ Links ]

Platenkamp, R. J., (1985). Temperature Distribution Around Water Injectors: Effects on Injection Performance. Paper SPE 13476 Middle East Oil Technical Conference and Exhibition held in Bahrain, March 11-14.        [ Links ]

Tiab, D., (1995). Analysis of Pressure and Pressure Derivative without Type-Curve Matching: 1- Skin Factor and Wellbore Storag. J. Petroleum Scien and Engineer. January 1995, 12 (3): 171-181.        [ Links ]