ABSTRACT

Although, the radial difussivitity equation has been solved for a single-fluid phase flow, in some cases more than one phase flows from the reservoir to the well; therefore, the single-phase solution has been previously extended to multiphase flow without losing a significant degree of accuracy. Practically, there exist two ways of dealing with multiphase flow: The Perrine method, Perrine (1956) which basically replaces the single-phase compressibility by the multiphase compressibility so that each fluid is analyzed separately using the concept of mobility. The other one is the use of pseudofunctions which have been found to be the best option. The TDS technique has been widely applied to a variety of scenarios. It has been even tested to successfully work on condensate systems with the use of pseudofunctions, Jokhio, Tiab and Escobar (2002). However, equations for estimation of phase permeability, skin factor and drainage area has not neither presented nor tested. In this article, we present new versions of a set of equations of the TDS technique to be applied to multiphase flow following the Perrine method along with a previously presented way of estimation of the absolute relative permeability. We successfully applied the proposed equations to synthetic and field examples.

Key words: perrine method, mobility, radial flow, relative permeabilities.

RESUMEN

Aunque, la ecuación de difusividad ha sido resuelta para flujo monofásico, en algunos casos más de un fluido fluye del yacimiento hacia el pozo; por tanto, la solución monofásica se ha aplicado previamente a flujo multifásico sin perder un significante grado de exactitud. Practicamente, existen dos maneras de de tratar con flujo multifásico: El método de Perrine, Perrine (1956), en el cual básicamente se reemplaza la compresibilidad monofásica por la compresibilidad multifásica de modo que cada fluido se analiza separadamente usando el concepto de movilidad. La otra manera es usar las pseudofunciones. Esta se considera como mejor opción. La técnica TDS se ha extendido ampliamente a una gran variedad de escenarios. Incluso, se ha aplicado satisfactoriamente en sistemas de condensados mediante pseudofunciones, Jokhio,Tiab y Escobar (2002). Sin embargo, las ecuaciones para estimar la permeabilidad de las fases, el daño y el área de drene ni se han presentado y por tanto tampoco se han probado. En este artículo, se presentan nuevas versiones de ecuaciones de la técnica TDS para usarse en flujo multifásico siguiendo el método de Perrine, como también se conjuga con una aproximación ya expuesta en la literatura para estimar la permeabilidad absoluta del medio. Las ecuaciones desarrolladas se aplicaron satisfactoriamente a ejemplos simulados y de campo.

Palabras Clave: método de Perrine, mobilidad, flujo radial, permeabilidades relativas.

INTRODUCTION

Perrine (1956) introduced a method of analysis for multiphase flow from the method of single-fluid phase flow by replacing the single-phase compressibility by the multiphase compressibility and replacing the singlephase mobility by the sum of the mobilities of the fluids in the multiphase flows. The method assumes that (i) saturation gradients must be small and, therefore, are neglected which is not the case in reality, (ii) pressure gradients must be small, which is not the actual case and (iii) capillary pressure between the phases must be negligible, which is usually the case in for pressure transient testing. These assumptions are, however, justified by Martin (1959). Because of these assumptions, the Perrine approach has some limitations. For instance, as pointed out by Weller (1966) as the saturation increases the results are less reliable. The phase permeabilities can be underestimated, Chu , Reynolds and Raghavan (1986), and the skin effect can be overestimated if flow is blocked by gas in the near wellbore region, Ayan and Lee (1988).

Even though the Perrine approach is used in this work, it is worth to say that there exist more rigorous methods provided in the literature for analyzing multiphase flow without requiring the knowledge of the permeability curves. The reader should refer to Al-Khalifah, A-J.A., Aziz and Horne (1987) and Serra, Peres and Reynolds (1990) for further information.

A modern interpretation tool known as Tiab's Direct Synthesis (TDS) technique which employs the pressure and pressure derivative curves to interpret pressure buildup and drawdown tests without using type-curve matching has been introduced by Tiab (1993 and 1995). Because of its simplicity and practicality, this technique is used in most commercial softwares, although the name TDS has been never shown up. The TDS technique has been extended to include many cases as possible. Few recent examples of them are presented by Moncada et al. (2005), Molina, Escobar, Montealegre-M. and Restrepo (2005), Escobar et al. (2007a, 2007b, and 2007c). New basic equations to include multiphase flow are presented here.

THEORY

According to Perrine (1956) a "total" flow mobility is calculated as Equation 1:

Then, the radial difussivity equation can be expressed in field units as Equation 2:

According to Martin (1956) the total compressibility of the system can be expressed as Equation 3.a:

It is not the attempt of this work to study neither the sensitivity of the compressibility nor the effect of dissolved gas on the solution, but to provide new equations for application of the TDS technique for the case of multiphase flows. The reader is invited to use Equation 3.a for accuracy, however, for practical purposes Equation 3.b may be used instead:

The total flow rate is then Equation 4,

Application of the above relationships to the equations presented by Tiab (1993) leads to estimate the wellbore storage coefficient by Equation 5 and Equation 6:

For pressure drawdown tests, ΔP = P_i - P_wf. For pressure buidup tests, ΔP = P_ws - P_wf (Δt = 0). Each phase's mobility ought to be determined from the following expressions, Equations 7, 8 and 9:

Being (t*ΔP')r the value of the pressure derivative during radial flow regime. If free gas is present, then, Equation 9 should be reformulated as Equation 10:

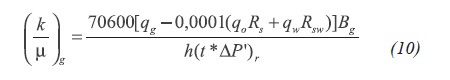
The total mobility can be estimated either by Equations 1 or by Equations 11:

Since the unit-slope line is the same for the pressure and pressure derivative curve, at the intersection point we have Equation 12:

Therefore, suffix r in Equations 5 and 11 can be changed to i to indicate that these relationships can be applied at the point of intersection between the radial-flow line and early unit-slope line, t_i, which can also be applied to confirm the system mobility by Equation 13:

By dividing the pressure equation and pressure derivative equation during radial flow regime and solving for skin factor, Tiab (1993) obtained an equation to estimate the skin factor using a point of pressure and pressure derivative read at any arbitrary time, t_r, during the infinite-acting behavior. The multiphase equation is Equation 14:

ΔP_r is the value of pressure read at the time t_r. The semilog slope is equal to the the value of pressure derivative during radial flow multiplied by the natural log of 10 then, the pressure drop due to skin factor is estimated as Equation 15:

Tiab (1993) also presented several correlations to estimate reservoir permeability, skin factor and wellbore storage coefficient which use the time and pressure derivative values read at the maximum point of the pressure derivative (peak). These correlations which were rearranged for multiphase flow to estimate total fluid mobility, wellbore storage coefficient and skin factor are presented below, Equation 16, 17, 18, 19 and 20:

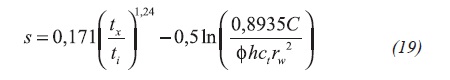
Suffix x refers to the maximum pressure derivative. Tiab (1995) also derived an equation to estimate reservoir drainage area based upon the intersection point of the unit-slope pseudosteady state line presented during late time and the radial-flow regime line which was named t_rpi. This equation, for multiphase flow, results to be Equation 21:

Recently, Kamal and Pan (2008) formulated a practical methodology to estimate reservoir absolute permeability and average fluid saturations from twophase well test data which is used in this work for complementary purposes. To apply the methodology, first estimate oil and water effective permeabilities using Equations 7 and 8, respectively. Then, estimate the permeability ratio k_o/kw and find water saturation, S_w, from a plot similar to Figure 1. With the S_w value just obtained enter into the relative permeability plot, like Figure 2, and find either water or oil relative permeabilities. Then, estimate absolute permeability using either Equations 22 or 23.

EXAMPLES

Synthetic example

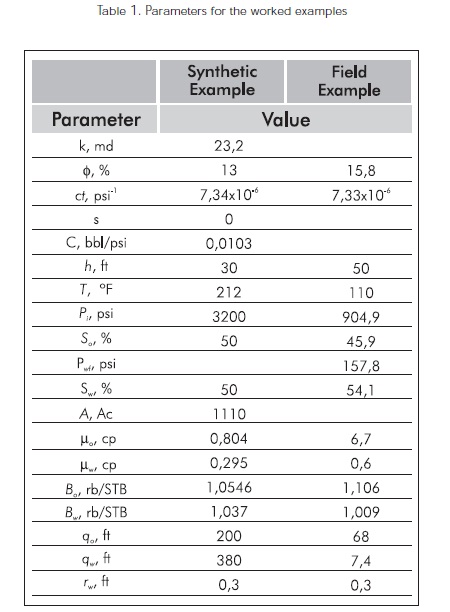
A commercial well test interpretation software was used to generate the drawdown test using the input information given in Table 1. The generated pressure data are reported in Table 2. The software used a power-law model to generate the relative permeability information provided in Figures 1 and 2.

Solution

From the pressure and pressure derivative plot, Figure 3, the following information was read with the help of a domestic software: t_r = 13,89 hr, ΔP_r = 586,57 psi, (tΔ*P')_r= 48,68 psi, t_i = 0,0199 hr, t_x = 0,2751 hr, (t*ΔP')_x = 188,055 psi, and t_rpi= 361,29 hrs. The effective permeabilities for oil and water are 8,2097 md and 5,6268 md, respectively, obtained from Equations 7 and 8. Also, for these parameters, values of 8,201 md and 5,6268 md were obtained using Equation 13. Besides, the correlation given in Equation 16 provides values of oil and water effective permeabilities of 8,034 and 5,507 md, respectively. The wellbore storage coefficient was estimated to be 0,01032 bbl/psi from Equation 5 and 0,01033 bbl/psi from correlation Equation 18. A skin factor of 0,1135 was found with Equation 13 and -0,117 from correlation Equation 19. Finally, a drainage area of 1096,3 Ac was calculated with Equation 21. This value matches well the one of 1110 Ac presented as input data in Table 1. The permeability ratio k_o/k_w resulted to be 8,21/5,63 = 1,4582. This value is used in Figure 1 to obtain a water saturation value of 0,52 which leads to a reading of k_ro = 0,32 from Figure 2. An absolute permeability of 25,6 md was estimated using Equation 22 which closely agrees with the value of 23,3 md reported in Table 1.

Field Example

A buildup pressure test was run in a well located in the middle valley of the Magdalena River in Colombia, South America. Information concerning to well, fluid and reservoir properties is provided in Table 1. As for the first example, a power-law model to generate the relative permeability. Pressure data are reported in Table 2 and 3.

Solution

From the pressure and pressure derivative plot, Figure 3, the following information was read: tr = 31,93 hr, ΔPr = 787,17 psi, (t*ΔP')r = 66,02 psi, ti = 0,4326 hr, and trpi = 43,7 hr. An oil effective permeability was estimated to be 10,7924 and 10,7809 md using Equations 7 and 13, respectively. From the pressure derivative plot, Figure 4, we observe that the wellbore storage decreases and the radial flow is developed at about 8 hr. It changes at about 16 hr developing a new plateau, possibly, reflecting a fault. The pseudosteady state is seen after 60 hr of testing.

A water effective permeability of 0,096 and 0,0958 with respectively found using Equations 8 and 13. The wellbore storage coefficient was estimated to be 0,02257 bbl/psi either Equations 5 and 13. For comparative purposes, see Figure 7, a wellbore storage coefficient of 0,02 bbl/psi was found with a commercial software. Equation 14 was used to estimate a skin factor value of -1,4821 and the drainage area resulted to be 5,0805 Ac with Equation 23. The permeability ratio ko/kw resulted to 112,4. This value is used in Figure 5 to obtain a water saturation value of 0,3 which allows us to read a value of kro of 0,83 from Figure 6. An absolute permeability of 13 md was estimated using Equation 22. It was also found from a commercial software, Figure 7, that the permeability was of 12,11 md, which closely agrees with the estimated value of 13 md from this study. Further analysis was not carried out since the pressure derivative found in this work differs in the final portion from the one reported by the commercial software, Figure 7.

ANALYSIS OF RESULTS

CONCLUSIONS

For multiphase flow, new equations are introduced to the TDS technique for estimation of phase permeabilities, wellbore storage coefficient, skin factor and reservoir drainage area. The application of the equations was verified through field and simulated well test data.

ACKNOWLEDGMENTS

The authors gratefully acknowledge the financial support of Universidad Surcolombiana (Neiva, Huila, Colombia) for the completion of this study.

REFERENCES

Al-Khalifah, A-J. A., Aziz, K., & Horne, R.N. (1987). A new approach to miltiphase well test analysis. SPE 62^nd Annual Technical Conference and Exhibitio, Dallas, TX., Sept. 27-30. SPE 16743.        [ Links ]

Ayan, C., & Lee, W. J. (1988). Multiphase pressure buildup analysis: field examples. SPE California Regional Meeting, Long Beach, CA., March 23-25. SPE 17142.        [ Links ]

Chu, W-C., Reynolds, A. C., & Raghavan, R. (1986). Pressure transient analysis of two-phase flow problems. SPE Formation Evaluation, April, 51-164.        [ Links ]

Escobar, F. H., Ibagón, O. E., & Montealegre-M, M. (2007a.). Average reservoir pressure determination for homogeneous and naturally fractured formations from multi-rate testing with the TDS Technique. J. Petroleum Scien. and Engineer., 59: 204-212.        [ Links ]

Escobar, F. H., & Montealegre-M., M. (2007b.). Application of TDS technique to developed reservoirs. J. Petroleum Scien. and Engineer., 55: 252-258.        [ Links ]

Escobar, F. H., Hernández, Y. A., & Hernández, C. M. (2007c.). Pressure transient analysis for long homogeneous reservoirs using TDS technique. J. Petroleum Scien. and Engineer., 58 (1-2): 68-82.        [ Links ]

Jokhio, S. A., Tiab, D., & Escobar, F. H. (2002). Forecasting oil and water production from gas condensate wells. SPE Annual Technical Conference and Exhibition, San Antonio, TX, Sept. 29-Oct. 2. SPE 77549.        [ Links ]

Kamal, M. M., & Pan, Y., (2008). Use of transient data to calculate absolute permeability and average fluid saturations. SPE Western Regional and Pacific Section AAPG Joint Meeting, Bakersfield, CA. March 31-April 02. SPE 113903.        [ Links ]

Martin, J. C. (1959). Simplified equations of flow in gas drive reservoirs and the theoretical foundation of multiphase pressure buildup analysis. Petroleum Transaction, AIME, 216: 321-323, also SPE Paper 1235-G.        [ Links ]

Molina, M. D., Escobar, F. H., Montealegre-M, M., &.Restrepo, D. P. (2005). Application of the TDS technique for determining the average reservoir pressure for vertical wells in naturally fractured reservoirs. CT&F - Ciencia, Tecnología y Futuro, 2 (6), 45-55.        [ Links ]

Moncada, K., Tiab, D., Escobar, F. H., Montealegre-M, M., Chacon, A., Zamora, R.A., & Nese, S. L.(2005). Determination of vertical and horizontal permeabilities for vertical oil and gas wells with partial completion and partial penetration using pressure and pressure derivative plots without type-curve matching. CT&F - Ciencia, Tecnología y Futuro, 2 (6), 77-95.        [ Links ]

Perrine, R. L. (1956). Analysis of pressure buildup curves. Drilling and Production Practices, API, 482-509.        [ Links ]

Serra, K.V., Peres, A. M. M., & Reynolds, A. C. (1990). Well-Test analysis for solution-gas-drive reservoirs: part III - a unified treatment of pressure-squared method. SPE Formation Evaluation, June, 141-150.        [ Links ]

Tiab, D. (1993). Analysis of pressure and pressure derivative without type-curve matching: 1- skin and wellbore storage. J. Petroleum Scien. and Engineer., 12: 171-181. Also Paper SPE Production Operations Symposium, Oklahoma City, OK. March 21 - 28. 203-216. SPE 25423.        [ Links ]

Tiab, D. (1995). Analysis of pressure and pressure derivatives without type-curve matching-III. vertically fractured wells in closed systems. SPE Western Regional Meeting, Anchorage, Alaska. May 26 - 28. SPE 26138.        [ Links ]

Weller, W. T. (1966). Reservoir performance during twophase flow. J. Petroleum Technol., 240-246. Also SPE Paper 1334.        [ Links ]