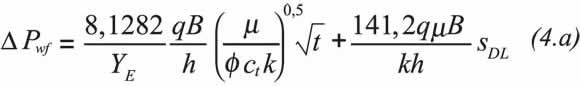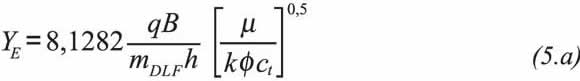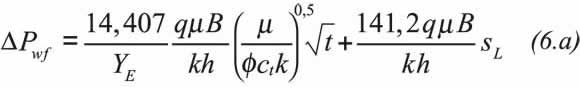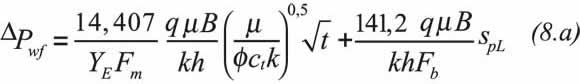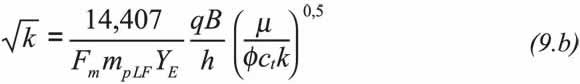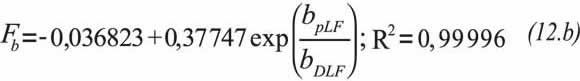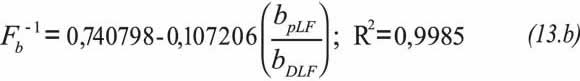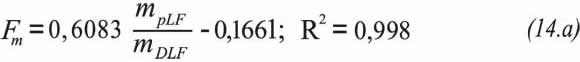Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
CT&F - Ciencia, Tecnología y Futuro
Print version ISSN 0122-5383On-line version ISSN 2382-4581
C.T.F Cienc. Tecnol. Futuro vol.3 no.5 Bucaramanga Jan./Dec. 2009
STRAIGHT LINE METHODS FOR ESTIMATING PERMEABILITY OR WIDTH FOR A TWO-ZONE COMPOSITE CHANNELIZED RESERVOIR
Freddy-Humberto Escobar1*, Matilde Montealegre-Madero1* and Daniel Carrillo-Moreno2*
1 Universidad Surcolombiana, Neiva, Huila, Colombia
2 PEMEX E&P, Cd. del Carmen, Campeche, México
e-mail: fescobar@usco.edu.co
(Received March 13, 2009; Accepted November 11, 2009)
*To whom correspondence may be addressed
ABSTRACT
Some well pressure tests conducted in channelized systems which result from either fluvial deposition or faulting, cannot be completely interpreted by conventional techniques, since variation in facies or reservoir width are not normally recognized yet in the oil literature. In this case, the corresponding equations traditionally used for single-linear flow will provide inaccurate results. Therefore, they must be corrected. In this study, new equations to be used in conventional analysis for the linear flow (pseudo linear) regime formed during the acting of the anomaly - reservoir width or permeability - are introduced to the oil literature. The equations do not consider the simultaneous variation of both parameters. The proposed equations were validated by applying them to synthetic and field examples.
Keywords: linear flow, dual-linear flow, pseudo-linear flow, Cartesian plot, channel reservoirs, skin factor.
RESUMEN
Algunas pruebas de presión que se corren en formaciones alargadas que resultan de depósitos fluviales o fallas geológicas, no pueden interpretarse a plenitud mediante análisis convencional, debido a que se presentan cambios de "facies" o variaciones en el ancho del yacimiento, las cuales no están reconocidas en la literatura petrolera. Las ecuaciones no consideran la variación simultánea de ambos parámetros. En este caso, las respectivas ecuaciones que tradicionalmente se utilizan para la caracterización del flujo lineal único, proporcionarán resultados incorrectos. Por lo tanto, éstas deben corregirse. En este trabajo, se introducen a la literatura petrolera nuevas ecuaciones para complementar el análisis convencional para el flujo lineal (pseudo-lineal) que resulta cuando interviene la anomalía considerada - ancho de yacimiento o permeabilidad. Las ecuaciones propuestas se validaron mediante ejemplos simulados y de campo.
Palabras Clave: flujo lineal, flujo dual lineal, flujo pseudo lineal, gráfico Cartesiano, canal, factor de daño.
RESUMEN
Algumas provas de pressão que se correm em formações alongadas que resultam de depósitos fluviais ou falhas geológicas, não possam interpretarse a plenitude mediante análise convencional, devido a que se apresentam mudanças de "facies" ou variações na largura da jazida, as quais não estão reconhecidas na literatura petroleira. As equações não consideram a variação simultânea de ambos parâmetros. Neste caso, as respectivas equações que tradicionalmente se utilizam para a caracterização do flu×o lineal único, proporcionarão resultados incorretos. Portanto, estas devem corrigirse. Neste trabalho, é introduzido à literatura petroleira novas equações para complementar a análise convencional para o fluxo lineal (pseudo-lineal) que resulta quando intervém a anomalia considerada - largura de jazida ou permeabilidade. As equações propostas foram validadas mediante e×emplos simulados e de campo.
Palavras Chave: fluxo lineal, fluxo dual lineal, fluxo pseudo lineal, gráfico Cartesiano, canal, fator de dano.
NOMENCLATURE
B Formation volume factor, (bbl/STB)
b Intercept
ct Compressibility, (1/psi)
Fm Correction factor for the slope of the pseudo-linear flow regime
Fm Correction factor for the intercept of the pseudo-linear flow regime
h Formation thickness, (ft)
k Permeability, (md)
m Slope
P Pressure, (psi)
Pwf Well-flowing pressure, (psi)
Pws Static well pressure, (psi)
Pi Initial reservoir pressure, (psi)
q Flow rate, (BPD)
rw Well radius, (ft)
s Skin factor
t Time, (hr)
YE Reservoir width, (ft)
GREEK
Δ Change, drop
ø Porosity, fraction
μ Viscosity, (cp)
SUFFICES
D Dimensionless
DL Dimensionless referred to reservoir width
DL Dual-linear
DL Dual-linear flow
i Intersection or initial conditions
L Linear or single-linear
LF Linear or single-linear flow
pL Pseudo-linear
pLF Pseudo-linear flow
t total
w Well, water
SI METRIC CONVERSION FACTOR
Bbl × 1,589 873 E-01 = m3
cp × 1,0* E-03 = Pa-s
ft × 3,048* E-01 = m
ft2 × 9,290 304* E-02 = m2
psi × 6,894 757 E+00 = kPa
INTRODUCTION
Not many well test interpretation researches have been conducted in elongated reservoirs. However, among those, the most relevant are cited here. Escobar, Muñoz & Sepúlveda (2005) introduced a new flow regime e×hibiting a -0,5 slope on the pressure derivative curve once dual-linear flow has ended in elongated reservoirs which they named "parabolic" flow. Later, Sui, Mou, Bi, Deng & Ehlig-Economides. (2007) also found that depicted behavior and called it "dipolar flow". Escobar and Montealegre (2006) and (2007) studied the impact of the geometric skin factors on elongated systems and complemented the conventional technique for these types of systems, respectively. Escobar, Hernández & Hernández (2007a) introduced the application of the Tiab Direct Synthesis (TDS) for characterization of long homogeneous reservoirs providing new equations for estimation of reservoir area, reservoir width and geometric skin factors. Besides that, Escobar, Tiab & Tovar. (2007b) provided a way to estimate reservoir anisotropy when reservoir width is known in elongated systems since linear and radial flow regimes are presented. Escobar (2008) presented a summary of the advances in characterization of long and homogenous reservoirs using pressure transient analysis. The purpose of this work is to complement the conventional technique to account for these new scenarios.
The motivation for this work was to determine the changes in reservoir width observed in some Colombian fields found in the Magdalena River Basin (example 3.3). However, the work was extended to consider changes in reservoir permeability in long and narrow reservoirs, although these types of changes have not been actually found by the authors. A simultaneous variation of both parameters can be easily simulated; however, in practice, to establish the degree of change of each parameter is not easy, even by using simulation, since many combinations of permeability-reservoir width changes can provide the same pressure behavior and pressure derivative behavior. Therefore, this situation is out of the scope of this work.
SIMULATION EXPERIMENTS
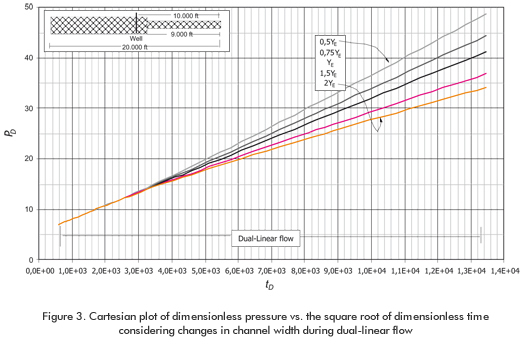
Multiple simulation runs were performed to understand the pressure-transient behavior throughout long reservoirs considering variations of either permeability or reservoir width. The study was divided into two parts to consider the variation or anomaly for: i) after dual-linear flow, Figures 1 and 2, and ii) during dual-linear flow regime, Figures 3 and 4.
The following observations apply to both cases. Once dual-linear flow finishes, it is observed in Figures 1 and 4, that as permeability increases the slope also increases and so does its intercept. For all cases when both slope and intercept changes, it cannot be referred as single-linear flow regime, since a new different equation will result. Because the shape of the streamlines still displays parallel vectors, then the behavior is still linear. For labeling purposes, it is called here pseudo-linear flow regime.
For changes higher than those shown in here, the straight line may not be seen; therefore, the proposed methodology will not apply.
Figures 2 and 3 display the effect of changes in reservoir width. For reductions in reservoir width, there will be an increase in the slope of the straight line during pseudo-linear flow. Also, as the reservoir width increases, the intercept of the straight line becomes larger.
MATHEMATICAL FORMULATION
The dimensionless time variables used by Escobar et al. (2007a) were:
The dimensionless pressure function defined by Earlougher (1977) as:
Escobar et al. (2007a) and Escobar and Montealegre (2007) have described the differences between the dual-linear flow and the single-linear flow occurring in elongated systems. Their governing equations are:
After replacing Equations 1 and 2 into Equation 3.a, Escobar and Montealegre (2007) found:
For pressure buildup analysis, application of time superposition is required, therefore Equation 4.a becomes:
Equations 4.a and 4.b imply that a Cartesian plot of ΔP vs. either t0,5 or [(tp+Δt)0,5-Δt0,5] will yield a straight line during dual-linear flow behavior which slope, mDLF, and intercept, bDLF, are used to obtain reservoir width, YE, and dual linear skin factor, sDL, according to:
By the same token, Escobar and Montealegre (2007) replaced Equations 1 and 2 into Equation 3.b and found very similar equations for linear flow (they only differ in the constant):
However, in order to account for pseudo-linear flow, the slope and intercept of Equations 6.a and 6.b have to be divided by correction factors so an accurate equation is obtained, such as:
For pressure buildup analysis:
Equations 8.a and 8.b indicate that a plot of ΔP vs. either t0,5 or [(tp+Δt)0,5-Δt0,5] in Cartesian coordinates yield a straight line during pseudo-linear flow regime which slope, mpLF, and intercept, bpLF, are used to obtain either reservoir width, YE,pL, or permeability, kpL, and pseudo-linear skin factor, spL, respectively:
The total skin factor will then be:
The correction factors for the slope and intercept of Equations 8.a and 8.b, Fm and Fb, are found considering the variations of the slope and intercept of the pseudo-linear straight line related to the slope and intercept of the dual-linear flow straight line. These ratios are used to determine the respective correction factors.
a) The anomaly or change of property occurs during dual-linear flow regime. Figure 5 shows the behavior between the slope and intercept ratios with the correction factor for permeability contrast. Both behaviors display an excellent correlation. The correction factors are:
Figure 6 shows the behavior between the slope and intercept ratios with the correction factor for reservoir width variation. Again, excellent correlations are obtained. The correction factors are:
b) The anomaly takes place once dual-linear flow has vanished. The behavior between the slope and intercept ratios with the correction factor for permeability contrast is displayed in Figure 7 with excellent correlation coeffi-cients. The correction factors are:
Permeability changes after dual linear flow can be estimated only for 60% < k < 140%. Out of this range, the straight line may not be developed. The following correlations are obtained from Figure 8.
EXAMPLES
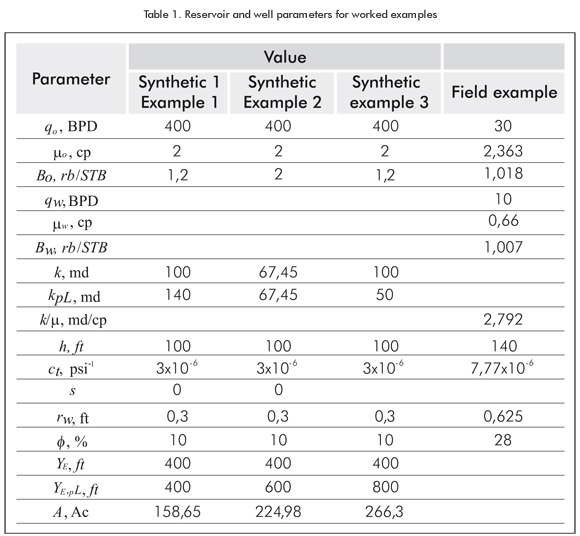
The synthetic examples presented here were numerically generated by a commercial well test interpretation software.
Simulated Example 1
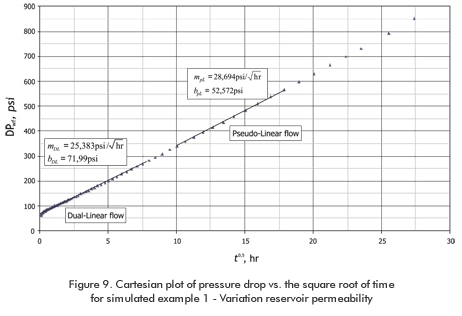
Figure 9 contains a pressure vs. the square root of time plot during the linear flow regimes for an elongated reservoir in which a variation in permeability from 100 md to 140 md was considered. Table 1 contains the input information to generate the example. Find permeability value at the other side of the anomaly and the geometric skin factors.
Solution
The following information was obtained from Figure 9.
mDLF = 25,383 psi/hr0,5
bDLF = 71,99 psi
mpLF = 28,694 psi/hr0,5
bpLF = 52,75 psi
Use Equations 5.a and 5.b to estimate reservoir width and geometric skin factor during dual-linear flow as:
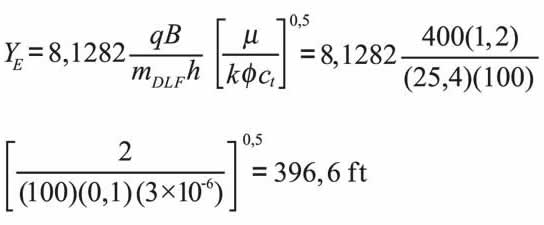

Determine the correction factors from Equations11.a and 11.b,
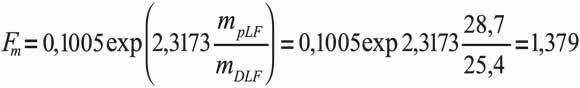

Find the permeability in the other side of the anomaly, Equation. 9.b and the pseudo-linear skin factor with Equation 9.c,

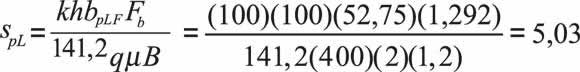
The expected value of kpL is 140 md. The difference should be due to the error of the correlation.
Simulated Example 2
A plot of pressure vs. the square root of time during the linear flow regimes for a channelized reservoir, in which reservoir width changes from 400 to 600 ft, is presented in Figure 10. Table 1 also contains the input information used for the simulation. Determine the other value of reservoir width, and skin factors.
Solution
The following information was read from Figure 10.
mDLF = 30,847 psi/hr0,5
bDLF = 108,81 psi
mpLF = 25,04 psi/hr0,5
bpLF = 153,5 psi
Calculate reservoir width and dual-linear skin factor with 5.a and 5.b, respectively:


Determine the correction factors using Equations 12.a and 12.b,

Estimate the reservoir width in the other side of the anomaly, Equation 9.a and the pseudo-linear skin factor with Equation 9.c,
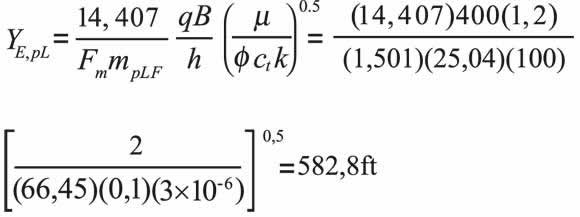

Simulated Example 3
The purpose of this example is to demonstrate the failure of the method for simultaneous variation of reservoir width and permeability. The input data is also given in Table 1. Determine the values of reservoir width and permeability.
Solution
In the pressure derivative plot, Figure 11, is observed that the dual-linear flow regime appears
between 0,35 and 8 hr and the pseudo-linear is slightly seen between 358 and 501 hr. Then, the following data was read from Figure 12.
mDLF = 25,41 psi/hr0,5
bDLF = 3.926,8 psi
mpLF = 11,12 psi/hr0,5
bpLF = 3.832,8 psi
Reservoir width is estimated with Equation 5.a:

Determine the correction factors for permeability and width which are obtained using Equations 11.a and 12.a,
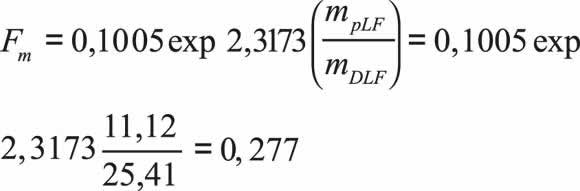
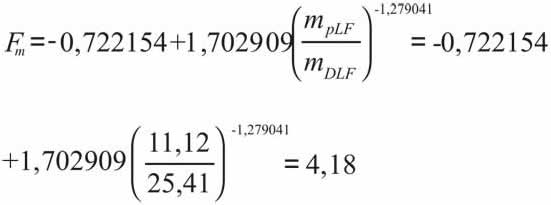
Permeability in the altered zone is obtained from Equation 9.b:
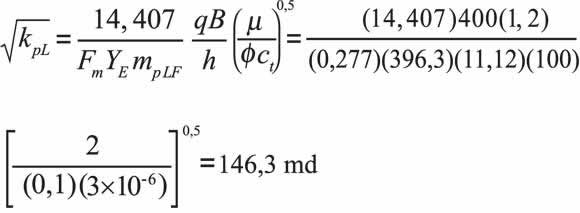
The new value of reservoir width is estimated using the permeability of 146,3 md in Equation 9.a:

The expected values of permeability and reservoir width were, respectively, 50 md and 800 ft. It is demonstrated that the methodology does not account for simultaneous changes in permeability and reservoir width.
Field Example
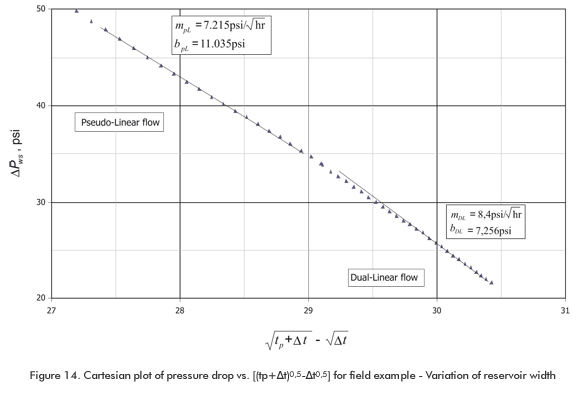
Figure 13 contains a pressure and pressure derivative plot for a pressure buildup test that was run in a well in a small oil reservoir located in the Magdalena River middle Valley Basin in Colombia, South America. The well flowed for 1.032 hr before shutting-in. After about 9 hrs, the pressure derivative curve should have gone slightly upwards and then, developed the single linear flow regime, as described by Escobar et al. (2007a). However, it went slightly down instead, and a half-slope straight line was developed because, we believe, the reservoir width increased. This line ends at about 27 hr and then a plateau is seen. Probably, this is due to the influence of an even wider reservoir zone. Information concerning reservoir, well and fluid properties for this test is reported in Table 1. The pressure vs. [(tp+Δt)0,5-Δt0,5] plot during the linear flow regimes for this well is given in Figure 14. It is required to determine the variation in reservoir width and linear skin factors.
Solution
According to the pressure derivative plot, Figure 13, the dual-linear flow is seen approximately between 3 and 9 hrs. It is followed by a pseudo-linear flow regime which occurs between about 12 and 27 hrs. The following information was read from Figure 14.
mDLF = 8,4 psi/hr0,5
bDLF = 7,256 psi
mpLF = 7,216 psi/hr0,5
bpLF = 11,03 psi
Estimate reservoir width, Equation 5.a, and dual-linear skin factor with Equation5.b:

It is worth to clarify that the viscosity of neither oil nor water is used in Equation 5.a. Instead, a total mobility, (k/μ)t, of 2,792 md/cp is used. See Table 1.

Determine the correction factors using Equations12.a and 12.b,


Find the reservoir width in the other side of the anomaly, Equation 9.a and the pseudo-linear skin factor with Equation 9.c,


ANALYSIS OF RESULTS
The simulated examples were worked with the purposes of verifying the equations. In the first synthetic example the permeability value was supposed to be 140 md. The estimation was 129,5 md involving an absolute deviation of 7,5%.
In the second synthetic example the expected value of reservoir width was 600 ft. We obtained an average reservoir width value of 582,8 ft indicating an absolute deviation of 2,9%. This indicates that the formulated equations are correct and, then, may be applied to field cases, such as the third example. These results agree with those from Escobar et al. (2008).
The pseudo-linear skin factor in the first example is slightly lower than the dual-linear one. This is probably due to the increment of reservoir permeability since no variation in the direction of flow is expected to occur, as it happened in the other two examples.
Since the methodology was not formulated for simultaneous variation in facies and reservoir width, it fails to provide reasonable answer as shown by the synthetic example 3.
CONCLUSIONS
- The well-known straight-line conventional method was complemented with the necessary relationships to characterize elongated reservoirs drained by vertical oil wells when either variations in permeability or reservoir width are presented. In this case, the single-linear flow regime equation is modified with some correction factors to account for the mentioned variations. Then, appropriate versions of the equations to estimate reservoir width and skin factors are provided. The equations were tested with synthetic examples and then applied to a field case. The equations are not intended to describe the simultaneous changes in facies and reservoir width since they fail for such case.
ACKNOWLEDGMENTS
The authors gratefully acknowledge the financial support of Universidad Surcolombiana (Neiva, Huila, Colombia) for the completion of this study.
REFERENCES
Earlougher, R. C., Jr. (1977). Advances in Well Test Analysis. Monograph Series, Vol. 5, SPE, Dallas, TX. [ Links ]
Escobar, F. H., Muñoz, O. F., Sepulveda, J. A. & Monte-alegre, M. (2005). New Finding on Pressure Response In Long, Narrow Reservoirs. CTYF - Ciencia, Tecnología y Futuro,2 (6), 151-160. [ Links ]
Escobar, F. H. & Montealegre-M., M. (2006). Effect of Well Stimulation on the Skin Factor in Elongated Reservoirs. CTYF - Ciencia, Tecnología y Futuro, 3 (2), 109-119. [ Links ]
Escobar, F. H., Hernández, Y. A. & Hernández, C.M. (2007a). Pressure Transient Analysis for Long Homogeneous Reservoirs using TDS Technique. Journal of Petroleum Science and Engineering, 58 (1-2), 68-82. [ Links ]
Escobar, F. H., Tiab, D. & Tovar, L.V. (2007b). Determination of Areal Anisotropy from a single vertical Pressure Test and Geological Data in Elongated Reservoirs.Journal of Engineering and Applied Sciences. 2(11), 1627-1639. [ Links ]
Escobar, F. H. & Montealegre, M. (2007). A Complementary Conventional Analysis For Channelized Reservoirs. CTYF - Ciencia, Tecnología y Futuro, 3 (3), 137-146. [ Links ]
Escobar, F. H. (2008). Petroleum Science Research Progress. Nova Publishers. Edited by Korin L. [ Links ]
Sui, W., Mou, J. Bi, L., Den, J. & Ehlig-Economides, C. (2007). New Flow Regimes for Well Near-Constant-Pressure Boundary. Paper SPE 106922, proceedings, SPE Latin American and Caribbean Petroleum Engineering Conference, Buenos Aires, Argentina. [ Links ]
Tiab, D. (1993). Analysis of pressure derivative without type-curve matching: Vertically fractured wells in closed systems. SPE 26138 at the 1993 SPE Western Regional Meeting, held May 26-28, Anchorage, Alaska. [ Links ]
Tiab, D. (1994). Analysis of pressure derivative without type-curve matching: Vertically fractured wells in closed systems. Journal of Petroleum Science and Engineering, 11, 323-333. [ Links ]