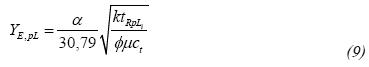Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
CT&F - Ciencia, Tecnología y Futuro
Print version ISSN 0122-5383On-line version ISSN 2382-4581
C.T.F Cienc. Tecnol. Futuro vol.4 no.1 Bucaramanga Jan./July 2010
2 Programa de Ingeniería de Petróleos, Universidad Surcolombiana, Av. Pastrana - Cra. 1, Neiva, Huila, Colombia
3 Activo Regional Exploratorio, PEMEX E & P, Ciudad del Carmen, Campeche, México
e-mail: fescobar@usco.edu.co matildelina2005@hotmail.com dcarrillom@pep.pemex.com
(Received, Jan. 29, 2010; Accepted May 26, 2010)
* To whom correspondence may be addressed
ABSTRACT
Due to geologic and tectonic events many reservoirs have an elongated geometry in which dual-linear and single-linear flow regimes may be developed. The single-linear flow may be altered by changes in facies (mobility) or reservoir width (composite reservoir). Therefore, it is desirable to identify and characterize these types of systems which lead to competent decisions and adequate reservoir management. The identification and determination of parameters for such reservoirs are conducted by conventional techniques (straight-line method), type-curve matching of pressure versus time and the Tiab's Direct Synthesis (TDS) technique. This last one has been lately presented for homogeneous and constant width reservoirs. In this paper, an extension of the TDS technique to incorporate variations in either mobility or reservoir width is presented. Several simulation experiments were run to understand the behavior of the reservoir under these new conditions. If the change of the mentioned parameters takes place after the dual- linear flow has ended a new half-slope line is observed on the pressure derivative curve. This new line is shifted upwards the original dual-linear line without regarding the variation of one of the studied parameter. When, the anomaly occurs during dual- linear flow the new half-slope line of the pressure derivative curve may be shifted upwards or downwards depending upon the magnitude of either mobility or reservoir width. This new line may not be referred as linear flow regime because it is really not. We have named it as pseudo-linear flow regime, instead. Therefore, a modification of the intercept of the ½-slope line from π0,5 for dual-linear flow regime to a greater or smaller value, which may be different from π (single-linear flow case) has to be considered in order to provide new equations for the estimation of new values of either permeability or reservoir width. The proposed methodology was successfully verified by interpreting both synthetic and field pressure tests for elongated oil reservoirs which involve changes in either mobility or reservoir width during the path of the transient wave.
Palabras clave: linear flow, radial flow, permeability, pressure tests, deposits facies.
RESUMEN
Debido a eventos geológicos y téctónicos muchos yacimeintos presentan geometría alargada en la cual se pueden desarrollar los flujos dual lineal y lineal único. El flujo lineal sencillo podría ser alterado por cambios en facies (movilidad) o cambios del ancho del yacimiento (yacimiento compuesto). Por ende, se desea identificar y caracterizar estos tipos de sistemas, lo que conducirá a decisiones competentes y una adecuada gerencia del yacimiento. La identificación y determinación de parámetros para tales sistemas se conduce mediante técnicas convencionales (método de la línea recta), curvas tipo de presión versus tiempo y la técnica de la síntesis directa de Tiab (TDS). Esta última ha sido presentada en yacimientos homogéneos de ancho constante. En este trabajo, se extiende la metodología TDS para incorporar variaciones ya sea en movilidad o ancho del yacimiento. Se corrieron varios experimentos numéricos para entender el comportamiento de un yacimiento bajo estas nuevas condiciones. Si el cambio de los parámetros mencionados toma lugar cuando termina el flujo dual lineal se observará una nueva pendiente de ½ en la curva de la derivada de presión. Esta nueva línea se encuentra desplazada hacia arriba de la línea original dual lineal sin considerar la variación de uno de los parámetros estudiados. Cuando la anomalía toma lugar durante el flujo dual lineal la nueva linea de la derivada con pendiente de ½ podría desplazarse hacia arriba o hacia abajo dependiendo de la maginitud de la variación de la movilidad o del ancho del yacimiento. Esta nueva línea no deberíe referirse como régimen de flujo lineal, porque no lo es. En su lugar la hemos llamado régimen de flujo pseudo-lineal. Por tanto, hay que considerar una modificación del intercepto de la linea de pendiente de ½ de π0,5 para flujo dual lineal a un valor mayor o menor, el cual es diferente de π (caso de flujo lineal único) para proporcionar nuevas ecuaciones para la estimación de nuevos valores de permeabilidad o ancho del reservorio. La metodología propuesta se verificó satisfactoriamente aplicándola a ejemplos de campo y sintéticos en yacimientos elongados que involucran cambios en movilidad o ancho del yacimiento durante el camino de la onda de transiente de presión.
Key words: flujo lineal, flujo radial, permeabilidad, pruebas de presión, yacimientos, facies.
INTRODUCTION
Many buildup and drawdown pressure tests are run in elongated reservoir systems. Linear flow regimes will develop during a transient pressure tests in this specific geometry. It is necessary to account for an appropriate identification and determination of reservoir parameters, including dimensions, when that is possible. Many reservoirs in the Magdalena River Valley Basin in Colombia, South America, display channelized behavior due to, probably, fluvial deposition.
The first solution to water influx in a linear aquifer was presented by Miller (1966). Afterwards, Nutakki & Mattar (1982) presented an investigation for infinite channel reservoirs using a vertical fracture approach with a pseudo skin factor. Their governing pressure equation possesses a wrong constant but they provided the first mathematical insights to work on long and narrow reservoir systems and provided a conventional straight-line methodology for well test interpretation. Ehlig-Economides & Economides (1985) presented an analytical solution for linear flow to a constant-planar source solution in drawdown tests. Their solution was also applied to interference testing by type-curve matching. Raghavan & Chu (1966) presented a method to estimate average pressure when radial flow conditions are nonexistent for linear and bilinear flow regimes which may be applicable to channel reservoirs. The results of flow simulations in geologically complex channelized reservoirs were introduced by Massonet, Norris & Chalmette (1993). Their well test analysis was performed by non-linear regression analysis and no interpretation technique was presented. Wong, Mothersele, Harrington & Cinco-ley (1986) presented new type curves to interpret pressure transient analysis for rectangular reservoirs. They used type-curve matching and conventional techniques to solve some field data examples. Their type curves allowed easy recognition of the late-time behavior for all possible well positions in the mentioned reservoir systems.
Escobar, Hernández & Hernández (2007a) introduced the application of the TDS technique for characterization of long and homogeneous reservoirs presenting new equations for estimation of reservoir area, reservoir width and geometric skin factors. They also corrected the pressure equation provided by Nutakki & Mattar (1982) and classified the linear flow regime in to two cathegories: (a) dual-linear flow regime when the flow takes along both sides of the well thoughtout the elongated reservoir part, and (b) single-linear flow regime when flow comes from one side of the reservoir. Escobar, Muñoz, Sepúlveda & Montealegre (2005) introduced a new flow regime exhibiting a negative half slope on the pressure derivative curve once duallinear flow has ended. They called this as parabolic flow. Sui, Mou, Bi, Den & Ehlig-Economides (2007) have also found this same behavior. However, they called it "dipolar flow". Later, Escobar & Montealegre (2006) studied the impact of the geometric skin factors on elongated systems. Characterization of pressure tests in elongated systems using the conventional method was presented by Escobar & Montealegre (2007). Also, Escobar, Tiab & Tovar (2007b) provided a way to estimate reservoir anisotropy when reservoir width is known in the mentioned systems from the combination of information obtained from the linear and radial flow regimes. Escobar (2008) presented a summary of the advances in characterization of long and homogenous reservoirs using transient pressure analysis.
Escobar, Hernández & Hernández (2007a) introduced the application of the TDS technique for characterization of long and homogeneous reservoirs presenting new equations for estimation of reservoir area, reservoir width and geometric skin factors. They also corrected the pressure equation provided by Nutakki & Mattar (1982) and classified the linear flow regime in to two cathegories: (a) dual-linear flow regime when the flow takes along both sides of the well thoughtout the elongated reservoir part, and (b) single-linear flow regime when flow comes from one side of the reservoir. Escobar, Muñoz, Sepúlveda & Montealegre (2005) introduced a new flow regime exhibiting a negative half slope on the pressure derivative curve once duallinear flow has ended. They called this as parabolic flow. Sui, Mou, Bi, Den & Ehlig-Economides (2007) have also found this same behavior. However, they called it "dipolar flow". Later, Escobar & Montealegre (2006) studied the impact of the geometric skin factors on elongated systems. Characterization of pressure tests in elongated systems using the conventional method was presented by Escobar & Montealegre (2007). Also, Escobar, Tiab & Tovar (2007b) provided a way to estimate reservoir anisotropy when reservoir width is known in the mentioned systems from the combination of information obtained from the linear and radial flow regimes. Escobar (2008) presented a summary of the advances in characterization of long and homogenous reservoirs using transient pressure analysis.
In all the above systems, the reservoir geometry was considered to be constant. This means the reservoir was assumed to have a perfect rectangular shape. To alleviate this assumption, Escobar, Montealegre & Carrillo- Moreno (2009) presented a solution for the dertemination of changes in either permeability or width in channelized systems using the conventional straight-line method. In that study, the single-linear flow regime equation is modified with some correction factors to account for the mentioned variations. Then, appropriate versions of the equations to estimate reservoir width and skin factors were provided. Finally, the present work complements the research recently presented by Escobar et al. (2009) to include the application of the pressure and pressure derivative for well test interpretation without the application of type-curve matching, also known as the TDS Technique. In this case, also, the governing pressure equations for the linear flow regimes were modified with some correction factors to account for the variations of either permeability or reservoir width.
NUMERICAL EXPERIMENTS
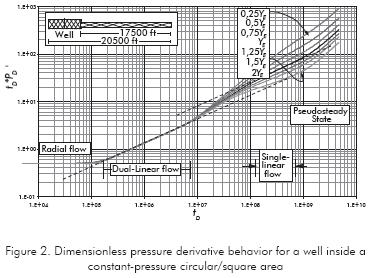
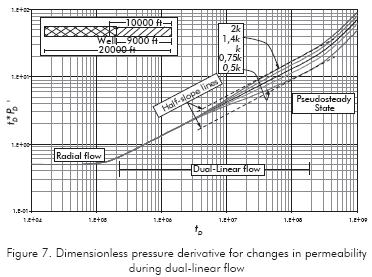
Multiple simulation runs were performed to understand the behavior of the pressure transient in long reservoirs when variations of either mobility or reservoir width are accounted for. We separated the study in two parts to consider the variation or anomaly for: i) once dual-linear flow has ended, Figures 1 to 5, and ii) during dual-linear flow regime, Figures 6 and 7.
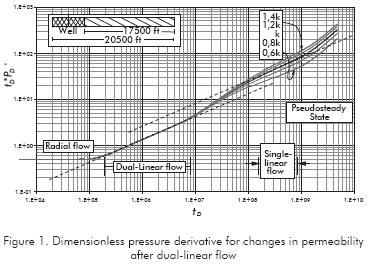
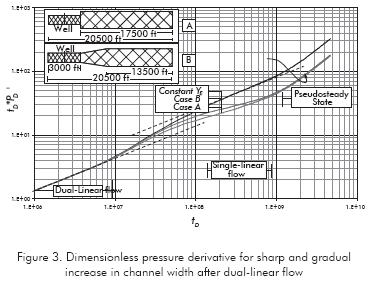
Case i. The intercept of the pressure derivative curve during dual-linear flow regime has a value of π0,5, Equation 1c, and the intercept of the single-linear flow pressure derivative curve is π, Equation 1d. If any of these intercepts is different, we are not referring to these specific flow regimes but others. Once dual-linear flow vanishes, it is observed in Figures 1 that as permeability increases pressure derivative also increases and so does its intercept. Notice also, during the anomaly, for all cases, the intercept of the pressure derivative curve is always higher than π0,5 (for dual-linear flow). Besides, for an increment in reservoir permeability, the intercept of the half-slope pressure derivative curve is always greater than π and gets lower than that for reductions of reservoir permeability. For all cases when the intercept of the half-slope line results different to π, it cannot be referred as single-linear flow regime. We have called it pseudo-linear flow regime, instead. It is worth to clarify that still linear flow is dealt with since the streamline vector are yet parallel. For higher changes than the ones shown in here, the half-slope line may not be seen; therefore, the proposed methodology will not apply.
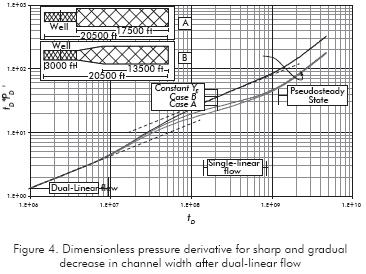
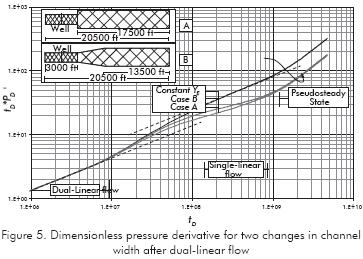
The effect of changes in reservoir width is shown in Figure 2. For reductions in reservoir width, there will be an increase in the pressure derivative curve over the single-linear flow straight-line pressure derivative. As the reservoir width increases, the intercept of the half-slope line becomes lower than π, and, even lower than π0,5 when the reservoir width is two folded. Figures 3 and 4 just show that abrupt or gradual changes in reservoir width may be unnoticed from a pressure test. For more than one increasing in reservoir width, a plateau in the pressure derivative may be seen due to the change in path of the streamlines. This behavior is observed in Figure 5.
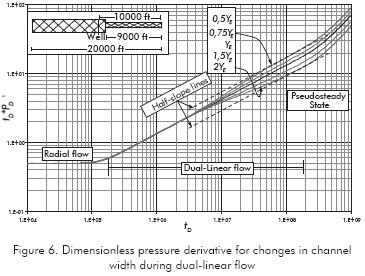
Case ii. The intercept of the pseudo-linear flow regime pressure derivative reduces as the reservoir width increases, see Figure 6, and increases as permeability increases, Figure 7. Contrary to case i, the intercept takes values lesser than π0,5.
MATHEMATICAL FORMULATION
Escobar et al. (2007a) have differentiated the linear flow regimes occurring in long and narrow reservoirs as dual-linear, when the transient wave travels along both sides of the reservoir, and single-linear when the well is off-centered inside the reservoir and the wave has reached one of the extreme reservoir boundaries so the disturbance travels along one side of the reservoir. The respective pressure derivative equations only differ on the intercept value. The governing pressure and pressure derivative equations for these flow regimes are:
Where the dimensionless quantities are defined by:
For the dual-linear case, Escobar et al. (2007a) developed the below given expressions to estimate reservoir width, drainage area and dual-linear skin factor.
As seen in the dimensionless pressure derivative plot of Figures 1 through 6, another half-slope straight line is observed after the dual-linear flow regime vanishes which is not considered to be the linear flow regime, instead we have call it here as "pseudo linear" flow and it is labeled with suffix pL. Then, using any arbitrary point during this straight line, with coordinates tpL and (t*ΔP')pL, the governing equation of this new regime may developed.
By integration of the above equation will result:
The determination of α in the above equations requires to establish the intercept of the straight line in dimensionless form plus an appropriate correction to account for either changes in permeability (or mobility) or reservoir width. Estimation of the intercept of this straight line is achieved by:
The multiplier factor, FM, is found according to:
a) Anomaly occurs during dual-linear flow. As observed in Figures 5 and 6, the shifting upwards or downwards of the pressure derivative curves is a function of the gradual change in either reservoir width or mobility.
Figure 8 shows a perfect behavior between these parameters with respect to the shifting of the pressure derivative. Permeability changes during dual linear flow are given by the following correlation (R2=0,9998):
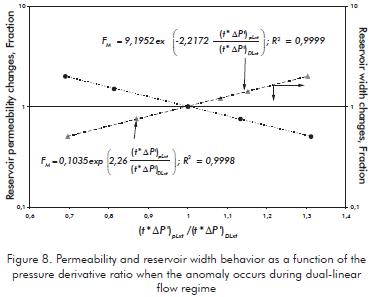
Notice that the pressure derivative values during the dual-linear and pseudo-linear flow regimes must be read at the same time, txt, of course, at least one of the half-slope line has to be extrapolated. Time of 1 hr is recommended. The reservoir width changes during dual-linear flow are correlated (R2=0,9999) by:
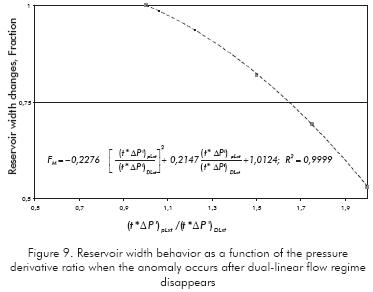
b) Anomaly occurs after thw dual-linear flow ends. This behavior is clearly seen in Figures 1 to 4. In this case, the pressure derivative always shifts upwards. Normally, the intercept of the dual-linear flow regime is higher than the other half-slope line, with a few exceptions. This means that the following correlation applies for pressure derivative ratios greater than 1. According to Figure 9, the developed correlation (R2=0,9999)is:
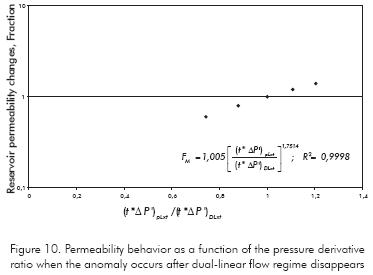
Permeability changes after dual-linear flow can be estimated only for variations of 60 % < k < 140 %. Out of this range, the 0,5-slope line may not be seen. The following correlation (R2=0,9998)is obtained from Figure 10.
For reservoir width changes, replace the dimensionless quantities given by Equations 2b, 2c and 2e in Equation 4a and solve for the value of the reservoir width in the other side of the reservoir variation, YE,pL:
During radial flow regime, the dimensionless pressure derivative value is 0,5. At the intercept of this line with the pseudo-linear pressure derivative line, tRlPi, given by Equation 4a, after replacing the dimensionless quantities, will result the following expression:
The pseudo-linear skin factor is obtained by dividing Equation 4b by 4a and solving for spL,
Since the pressure derivative during late-time pseudosteady state regime is given by,
At the point of intersection, referred here as tpLpssi, between this line with the pseudo-linear pressure derivative line will result the following equation once the dimensionless variables have been replaced:
Also, the intersection of the radial line with the pseudosteady-state line at a time called tRPSSi, will provide another equation for reservoir drainage area after plugging the dimensionless variables:
For changes in permeability, Equations 8, 9, 10 and 12 become:
Other Relationships
Tiab (1993, 1995) presented the following relationships for the estimation of wellbore storage coefficient, reservoir permeability and skin factor:
Finally, the total damage results as the summation of the mechanical plus the geometric skin factors, such as:
Step-by-Step Procedure
Step 1 - Build a log-log plot of pressure and pressure derivative, identify and draw the early pseudosteady- state, radial, dual-linear, pseudo-linear and late pseudosteady-state lines.
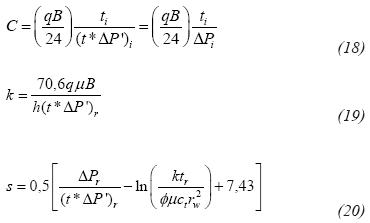
Step 2 - Estimate wellbore storage coefficient, permeability, skin factor and reservoir area using Equations 13, 18, 19 and 20, respectively, as indicated by Tiab (1993-1995).
Step 3 - Read the pressure and pressure derivative values, ΔPDL and (t*ΔP')DL, at any convenient point on the dual-linear flow regime, tDL, and find reservoir width, Equations 3a, and geometric skin factor, sDL.
Step 4 - Read the points of intersection of the dual-linear flow line with the radial line, tRDLi, and with the late pseudosteady-state line, tDLPPSi. Estimate reservoir width and reservoir area with Equations 3b and 3c, respectively.
Step 5 - Read the pressure and pressure derivative values, ΔPpL and (t*ΔP')pL, at any convenient point on the pseudo-linear flow regime, tpL. Extrapolate the linear flow lines and read the pressure derivative values, (t*ΔP')pLxt and (t*ΔP')DLxt at any convenient time txt in order to establish the vertical distance between the pressure derivative values. Also read the intersection points of the pseudo-linear flow line with the radial line, tRpLi, and with the late pseudosteady-state line, tpLPPSi.
Step 6 - According to the most probable situation, case i or ii, estimate the multiplier factor, FM, using either Equations 6a, 6b, 7a or 7b. Then, find α from Equation 5. 0,29293α is the dimensionless intercept of the pseudo-linear line.
Step 7 - For the case of change in permeability find the new permeability value, kpL, with Equation 14. Using this new value in Equations 15, 16 and 17 to compute reservoir width, geometric skin factor and reservoir area, respectively.
Step 8 - For the case of change in reservoir width, find the new reservoir width value, YE,pL, with either Equation 8 or 9. Use this new value in Equations 10 and 12 to determine geometric skin factor and reservoir area.
Step 9 - Estimate the total skin factor with Equations 21.
EXAMPLES
All the examples were also worked by Escobar et al. (2009).
Simulated example 1
Figure 11 shows the pressure and pressure derivative plot for an elongated reservoir in which a variation in permeability from 100 md to 140 md was considered. Table 1 contains the input information for the simulation. Determine the value of permeability at the other side of the anomaly, reservoir area and total skin factor.
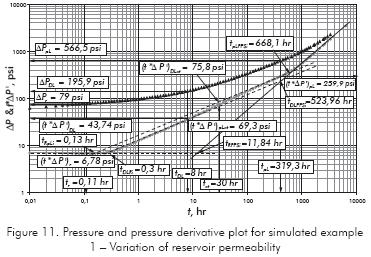
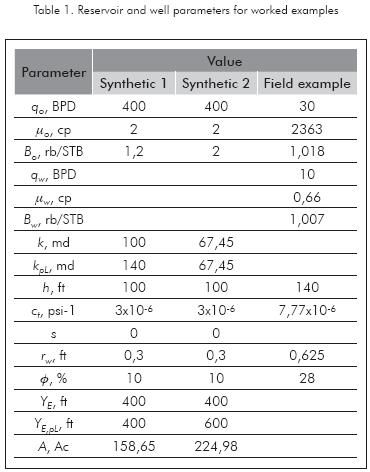
Solution. The following information was obtained from Figure 11.
It was determined a permeability value of 144,9 md as reported in Table 2 along with several other results.
Simulated example 2
A pressure and pressure derivative plot for a channelized reservoir in which reservoir width change from 400 to 600 ft is presented in Figure 12. Table 1 also contains the input information for the simulation. Determine the other value of reservoir width, reservoir area and total skin factor.
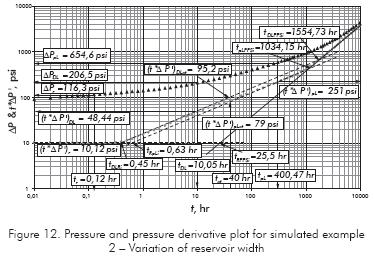
Solution. The following information was read from Figure 12.

An average reservoir width value of 595,5 ft was found for this example. Other results are summarized in Table 3.
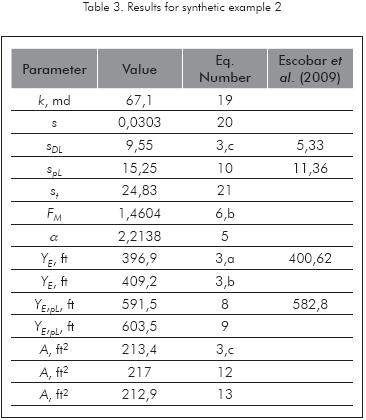
Field example
A pressure buildup test was run in a an oil well inside a small reservoir located in the Magdalena River Middle Valley Basin in Colombia, South America. As shown in Figure 13, the reservoir looks to have an elongated shape with variations in reservoir width. Information concerning reservoir, well and fluid properties for this test is reported in Table 1. The pressure and pressure derivative plot is provided in Figure 14. It is required to determine the variation in reservoir width and total skin factor.
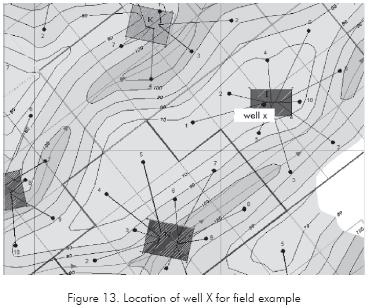
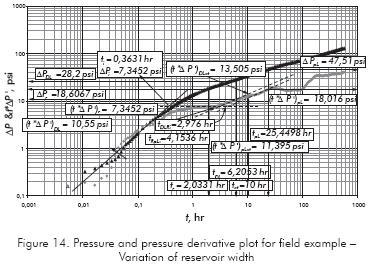
Solution. According to the pressure derivative plot, Figure 14, the radial flow regime shows up at about 1 hr and lasts a couple of hours. Dual-linear flow is seen approximately between 3 and 9 hrs. It is followed by a pseudo-linear flow regime (its intercept is smaller than the dual-linear flow) between about 12 and 27 hrs. Then, a plateau in the pressure derivative is observed between 30 and 90 hr which may indicate that the reservoir width increase more, as occurred in Figure 5. The following information was read from Figure 14.

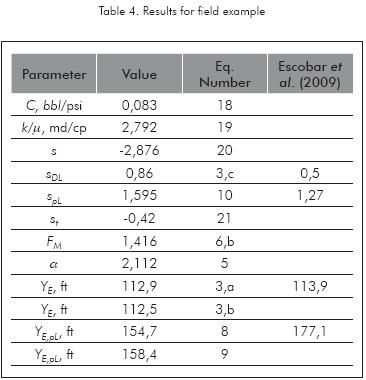
As reported in Table 4, along with more results, we found that the reservoir width increases from 112 ft to 155 ft.
ANALYSIS OF RESULTS
The synthetic examples were provided to verify the accuracy of the equations and the overall methodology. In the first simulated example, the expected permeability value was 140 md. We estimated 144,9 md, instead. An absolute deviation of 3,5 % was obtained. In the second synthetic example the expected value of reservoir width was 600 ft. We obtained an average reservoir width value of 595,5 ft indicating an absolute deviation of 0,75 %. These deviations lead to confirm that the formulated equation are correct and, then, may be applied to field cases, such as the third worked example.
Only in the first problem the value of the pseudolinear skin factor was lower than the dual-linear skin factor. This may be due to the increase in permeability since no change in the transient path is expected to happen. The results of changes in permeability and width agree with those reported by Escobar et al. (2009).
We tried to solve this problem using the non-linear regression analysis method of a commercial well test interpretation software. However, the numerical modeling does not account yet for the variations in reservoir width, as used in this paper, therefore, the goal was not achieved.
CONCLUSION
- The TDS technique was extended to characterize elongated oil formations (channels) for vertical oil wells when either variations in mobility or reservoir width are presented. In this case, the single-linear flow regime characterized by a dimensionless intercept of π is replaced by another one, called here pseudo-linear, which intercept is determined in this study for each particular case. Once the new intercept is found, individual equations for reservoir area, geometric skin factor, reservoir width and permeability are developed. The technique was successfully tested with field and synthetic examples.
ACKNOWLEDGMENTS
The authors gratefully thank the Highly Holy Trinity, Mary the Holy Mother of God and Saint Albert Magnus for all the blessings.
REFERENCES
Ehlig-Economides, C., & Economides, M. J. (1985). Pressure Transient Analysis in an Elongated Linear Flow Systems, SPEJ, December, 839-847. [ Links ]
El-Banbi, A. H., & Wattenberger, R. A. (1998). Analysis of Linear Flow in Gas Well Production. 1998 Gas Tech. Symp. Calgary, Alberta, Canada, 15-18 March. SPE 39972. [ Links ]
Escobar, F. H., Muñoz, O. F., Sepúlveda, J. A., & Montealegre, M. (2005). New Finding on Pressure Response In Long, Narrow Reservoirs. CT&F - Ciencia, Tecnología y Futuro. (2) 6, 106-111. [ Links ]
Escobar, F. H., & Montealegre, M. (2006). Effect of Well Stimulation on the Skin Factor in Elongated Reservoirs. CT&F - Ciencia, Tecnología y Futuro. (3) 2, 109-119. [ Links ]
Escobar, F. H., & Montealegre, M. (2007). A Complementary Conventional Analysis For Channelized Reservoirs. CT&F - Ciencia, Tecnología y Futuro. (3) 3, 137-146. [ Links ]
Escobar, F. H., Hernández, Y. A., & Hernández, C. M. (2007a). Pressure Transient Analysis for Long Homogeneous Reservoirs using TDS Technique. J. Petrol. Sci. Eng. 58 (1-2): 68-82. [ Links ]
Escobar, F. H., Tiab, D., & Tovar, L. V. (2007b). Determination of Areal Anisotropy from a single vertical Pressure Test and Geological Data in Elongated Reservoirs. J. of Eng. and Applied Sciences, 2 (11): 1627-1639. [ Links ]
Escobar, F. H. (2008). Petroleum Science Research Progress. Nova Publishers. Edited by Korin L. Montclaire. Recent Advances in Well Test Analysis for Long an Narrow Reservoirs, 431pp. [ Links ]
Escobar, F. H., Montealegre-M., M., & Carrillo-Moreno, D. (2009). Straight Line Methods for Estimating Permeability or Width for Two-Zone Composite Channelized Reservoirs. CT&F - Ciencia, Tecnología y Futuro. (3) 5, 107-124. [ Links ]
Massonet, G. J., Norris, R. J., & Chalmette, J-C. (1993). Well Test Interpretation in Geologically Complex Channelized Reservoirs, 68th Annual Technical Conference and Exhibition of the Society of Petroleum Engineers. Houston, TX. SPE 26464. [ Links ]
Mattar, L. (1997). Derivative Analysis without Type Curves. The Petroleum Society. Paper 97-51, 48th Annual Technical Meeting of the Petroleum Society, Calgary, Alberta, Canada. [ Links ]
Miller, F. G. (1966). Theory of Unsteady-State Influx of Water in Linear Reservoirs, J. Inst. Pet. 48 (467): 365-379. [ Links ]
Nutakki, R. & Mattar, L. (1982). Pressure Transient Analysis of Wells in Very Long Narrow reservoirs. 57th Annual Fall Technical Conference and Exhibition of the Society of Petroleum Engineers, Dallas, TX. SPE 11221. [ Links ]
Raghavan, R. & Chu, W.C., (1966). On the Determination of Reservoir Pressure when Radial-Flow Conditions are Nonexistent, Gas Technology Conference, Calgary, Alberta, Canada. SPE 35619. [ Links ]
Sui, W., Mou, J. Bi, L., Den, J., & Ehlig-Economides, C. (2007). New Flow Regimes for Well Near-Constant- Pressure Boundary. SPE Latin American and Caribbean Petroleum Engineering Conference, Buenos Aires, Argentina, April 15-18. SPE 106922. [ Links ]
Tiab, D. (1993). Analysis of Pressure and Pressure Derivatives without Type-Curve Matching-III. Vertically Fractured Wells in Closed Systems. SPE Western Regional Meeting, Anchorage, Alaska. SPE 26138. [ Links ]
Tiab, D. (1995). Analysis of Pressure and Pressure Derivative without Type-Curve Matching: 1- Skin and Wellbore Storage. J. Petrol. Sci. Eng.., Vol 12, 171-181. Also Production Operations Symp., Oklahoma City, OK. 203-216. SPE 25423. [ Links ]
Wong, D. W., Mothersele, C. D., Harrington, A. G., & Cinco-ley, H. (1986). Pressure Transient Analysis in Finite Linear Reservoirs Using Derivative and Conventional Techniques: Field Examples, 61st Annual technical Conference and Exhibition of the Society of Petroleum Engineers, New Orleans, LA. SPE 15421. [ Links ]