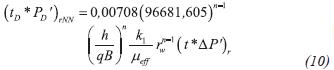Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
CT&F - Ciencia, Tecnología y Futuro
Print version ISSN 0122-5383On-line version ISSN 2382-4581
C.T.F Cienc. Tecnol. Futuro vol.4 no.2 Bucaramanga July/Dec. 2010
e-mail: fescobar@usco.edu.co jandres@usco.edu.co matildemm@hotmail.com
(Received, Aug. 2, 2010; Accepted, Dec. 9, 2010)
* To whom correspondence may be addressed
ABSTRACT
In many activities of the oil industry, engineers have to deal with completion and stimulation treatment fluids such as polymer solutions and some heavy crude oils which obey a non-Newtonian power-law behavior. When it is required to conduct a treatment with a non-Newtonian fluid in an oil-bearing formation, this comes in contact with conventional oil which possesses a Newtonian nature. This implies the definition of two media with entirely different mobilities. If a pressure test is run in such a system, the interpretation of data from such a test through the use of conventional straight-line method may be erroneous and may not provide a way for verification of the results obtained.
In this work, the signature of the pressure derivative curve is investigated to understand and ease the interpretation of the well test data in reservoirs with non-Newtonian power-law fluids. Specifically, the Tiab's Direct Synthesis (TDS) technique is implemented using some characteristics features found on the pressure and pressure derivative curves. Hence, new equations are introduced to estimate permeability, non-Newtonian bank radius and skin factor. Permeability can be verified. The proposed methodology was successfully verified by its application to an example reported in the literature and a synthetic case.
Keywords: radial flow, viscosity, reservoir characterization, pressure tests, mobility, permeability, mathematical model, pressure curve, Newtonian fluid, pressure analysis.
RESUMEN
En algunas actividades de la industria petrolera, los ingenieros tienen que tratar con fluidos de estimulación y completamiento tales como polímeros y algunos crudos pesados que obedecen un comportamiento no Newtoniano. Cuando se requiere un tratamiento con un fluido no Newtoniano en una formación productora de crudo, éste entra en contacto con el crudo convencional que posee naturaleza Newtoniana. Esto implica la definición de dos medios con movilidades completamente diferentes. Si allí se corre una prueba de presión, su interpretación mediante el método convencional de la línea recta podría conducir a resultados erróneos y tampoco permitiría la verificación de los resultados obtenidos.
En este trabajo se estudió la huella de la derivada de presión para entender y facilitar la interpretación de pruebas de presión en yacimientos con fluidos no-Newtonianos que obedecen la ley de potencia. Específicamente, se implementó la Síntesis Directa de Tiab (TDS) usando algunas características específicas halladas en la curva de la presión y la derivada de presión, de modo que se introdujeron nuevas ecuaciones para estimar permeabilidad, radio de la zona no Newtoniana y el factor de daño. La permeabilidad se puede verificar. La metodología propuesta se verificó satisfactoriamente mediante su aplicación a un problema reportado en la literatura y otro sintético.
Palabras Clave: flujo radial, viscosidad, caracterización de yacimientos, pruebas de presión, movilidad, permeabilidad, modelo matemático, curvas de presión, fluido newtoniano, análisis de presión.
1. INTRODUCTION
The oil literature contains several papers on the behavior of non-Newtonian fluids in porous media. Odeh and Yang (1979) derived a partial differential equation for fluid flow of power-law through porous media. They used a power-law function relating the viscosity to the shear rate. The power-law viscosity function was coupled with the variable viscosity diffusivity equation and a shear-rate relationship proposed by Savins (1969) to give a new partial differential equation and an approximate analytical solution. Ikoku (1979) has been the most outstanding researcher in the field of non- Newtonian power-law fluids modeling, as shown by Ikoku (1979), Ikoku and Ramey (1979a, 1979b, 1979c) and Lund and Ikoku (1981). Vongvuthipornchai and Raghavan (1987) used the pressure-derivative method for well test analysis of non-Newtonian fluids, however, the very first application to non-Newtonian behavior by the TDS technique was reported by Katime-Meindl and Tiab (2001).
Interpretation of pressure tests for non-Newtonian fluids is performed differently to conventional Newtonian fluids. During radial flow regime, Non-Newtonian fluids exhibit a pressure derivative curve which is not horizontal but rather inclined. As shown by Katime-Meindl and Tiab (2001), the smaller the value of n (flow behavior index) the more inclined the infinite-acting pressure derivative line. (See Figure 1).
This paper analyzes constant-rate injection tests and the extension of the TDS technique for a composite non-Newtonian/Newtonian system. For this purpose, a numerical simulator was built to generate the pressure and pressure derivative curves, and some characteristics points and lines were found on derivative curves to further develop analytical expressions which allow characterizing the reservoirs with fluids exhibiting non-Newtonian power-law behaviors.
2. MATHEMATHICAL MODEL
A partial differential equation for radial flow of non- Newtonian fluids that follow a power-law relationship through porous media was proposed by Ikoku and Ramey (1979b). Coupling the non-Newtonian Darcy's law with the continuity equation, they derived a rigorous partial differential equation:
This equation is nonlinear. For analytical solutions, a linearized approximation was also derived by Ikoku and Ramey (1979b):
Where:
and,
Ikoku and Ramey (1979b) solved Equation 1 using the predictor/corrector Douglas-Jones method for numerical solutions of nonlinear partial differential equations. They compared the results with the solution of the linear equation, (Equation 2). The errors introduced by the approximate linear equation were small and decrease with the increase in the value of the flow behavior index, n, and the increase of time.
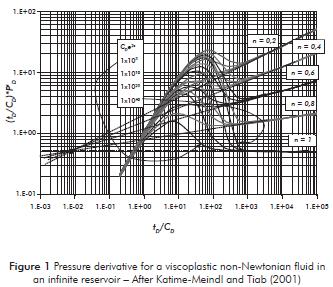
The system considered assumes radial flow of a non-Newtonian fluid and a slightly compressible Newtonian fluid through porous media. It is assumed that the reservoir is homogeneous, isotropic and of a constant thickness. The shape of the reservoir is cylindrical with finite outer radius. The non-Newtonian fluid is injected through a well in the center of the field. The fluid is considered to be non-Newtonian pseudoplastic which obeys the power law. The Newtonian fluid possesses a constant viscosity, as usually considered in well test analysis. It is also assumed piston-like of the Newtonian fluid by the non-Newtonian fluid. Figure 2 sketches the composite reservoir under consideration.
Martínez, Escobar and Montealegre (2010) solved numerically Equation 2 using the finite-difference approximation with the initial and boundary conditions normally used in well test analysis. Their results agree quite well with those reported by Ikoku and Ramey (1979b).
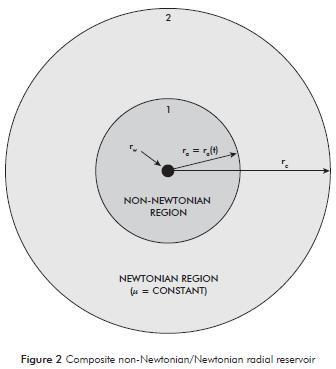
Since the pressure diffuses through a porous medium saturated with a non-Newtonian fluid, the pressure derivative has certain degree of inclination as the flow behavior index reduces its value. Once, the pressure diffusion reaches to the Newtonian zone, the pressure derivative forms a plateau, as expected, after an obvious transition period. Figure 3 illustrates such situation for different values of n.
The curves shown in Figure 3 were generated using the same input information given in the second example of Table 1. Notice than for n = 1, two different plateaus are observed since two different mobilities are dealt with. The smaller the n, the longer the time required to get the horizontal radial-flow line during the Newtonian zone.
3. FUNDAMENTAL EQUATIONS
The dimensionless pressure, PD, dimensionless time, tD, and dimensionless radius, rD, for each region are expressed as:
4. CHARACTERISTIC POINTS AND LINES
The formulation of the equations follows the philosophy of the TDS Technique, introduced by Tiab (1995). It means, several specific regions on the pressure and pressure derivative behavior are dealt with:
1). According to Katime-Meindl and Tiab (2001), the dimensionless equation for radial-flow regime derived in the non-Newtonian region without considering storage effects is:
The value of this derivative is:
Combination of Equation 10 and 12 leads to obtain:
Substituting Equation 4 into Equation 13 and solving for k1 yields:
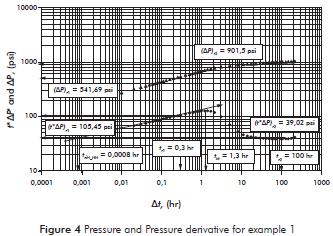
Where α is the slope of the pressure derivative curve on the non-Newtonian region and is defined as:
2). The governing pressure equation during non- Newtonian radial flow can be express by:
3). The skin factor, s1, can be obtained by dividing Equation 16 with Equation 12.
4). The radius of the injected non-Newtonian fluid bank is calculated using the following correlation (not valid for n = 1), obtained from reading the time at which the pressure derivative has its maximum value:
Lund and Ikoku (1981) found that the radius of the non-Newtonian fluid bank can be found using the radius investigation equation proposed by Ikoku and Ramey (1979):
Where t is the end time of the straight line found on a non-Newtonian Cartesian graph of ΔP vs.t1-n/3-n.
5). For the Newtonian region the permeability and skin factor were presented by Tiab (1995) as:
6). Intercept of the non-Newtonian/Newtonian radial flow lines. The infinite-acting dimensionless pressure derivative is given by:
Combination of Equation 22 and 12 will result in:
Rearranging,
Replacing the dimensionless quantities and solving for k1:
Where tiN_NN is the time of intersection of the non- Newtonian and Newtonian radial lines.
TDS has been always applied to either drawdown or buildup tests, Tiab (1993); therefore, application of this work to fall-off tests seems to have no problem as long as superposition do not affect the behavior of the pressure derivative. For variable injection rate time superposition should be applied; but, this is out of scope of this paper.
5. EXAMPLES
Example 1
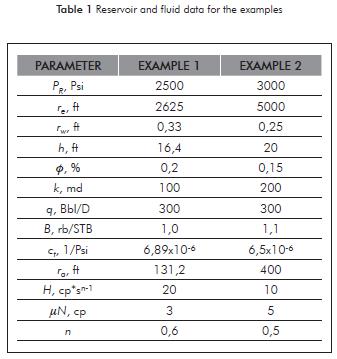
An constant-rate injection test for a well in a closed reservoir was generated by Lund and Ikoku (1981) with the data given in Table 1 and reported in Figure 4. It is required to estimate the permeability and the skin factor in each area and the radius of injected non-Newtonian fluid bank.
Solution. The log-log plot of pressure and pressure derivative against injection time is given in Figure 4. From that plot the following information was read:
tr1 = 0,3 hr ΔPr1 = 541,54 psi (t*ΔP')r1 = 105,45 psi
tr2 = 120 hr ΔPr2 = 991,5 psi (t*ΔP')r2 = 39,02 psi
tM = 1,3 hr tirN_NN = 0,0008 hr
First, α is evaluated with Equation 15 and the non- Newtonian effective fluid permeability is estimated with Equation 14.
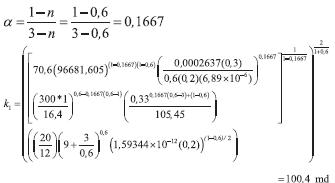
Equation 4 is used to find the effective viscosity, then, the skin factor in the non-Newtonian region is found with Equation 17,

Parameter G is estimated with Equation 3. This value is used in Equation 18 to find the non-Newtonian fluid bank,
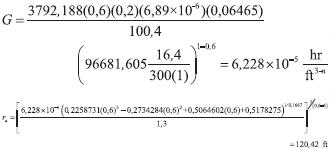
Equation 20 and 21 are used to estimate permeability and skin factor of the Newtonian zone:
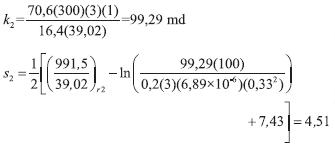
Equation 25 is used to re-estimate non-Newtonian effective fluid permeability:
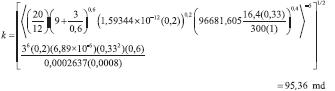
Lund and Ikoku (1981) obtained k1 = 100,64 md and ra = 116,5 ft using conventional analysis.
Example 2
Another injection test was simulated using the information from Table 1. Pressure and pressure derivative data are reported in Figure 5. It is required to estimate permeability and the skin factor in each area and the radius of non-Newtonian fluid bank.
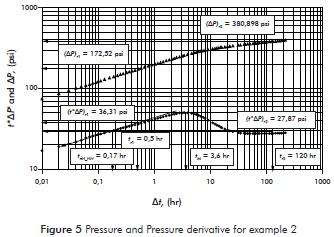
Solution. The following information was read from Figure 5:
tr1 = 0,5 hr ΔPr1 = 172,52 psi (t*ΔP')r1 = 36,31 psi
tr2 = 120 hr ΔPr2 = 380,898 psi (t*ΔP')r2 = 27,87 psi
tM = 3,6 hr tirN_NN = 0,17 hr
As for the former example, α is evaluated with Equation 15 and the non-Newtonian effective fluid permeability is estimated with Equation 14.
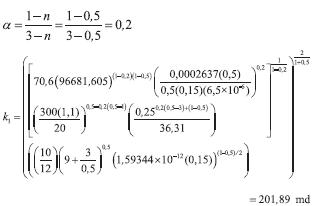
Effective viscosity is calculated with Equation 4, then, the skin factor in the non-Newtonian region is found with Equation 17,
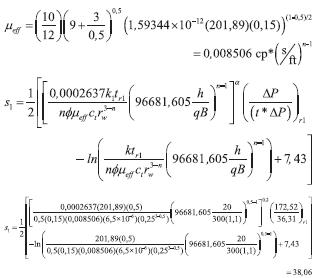
Equation 3 is used to find G. This value is used in Equation 18 to find the non-Newtonian fluid bank,

Permeability and skin factor of the Newtonian zone is, respectively, estimated with Equations 20 and 21,
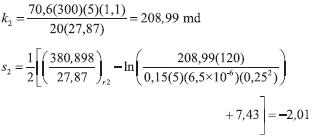
Equation 25 is used to verify the non-Newtonian effective fluid permeability,
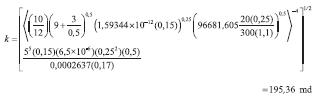
6. ANALYSIS OF RESULTS
The first example (Example 1 in Section 5) was also analyzed by Lund and Ikoku (1981), and we obtained results in close agreement with the values used by Lund and Ikoku (1981) to generate the synthetic test. On the other hand, the synthetic problem, second example (Example 2 in Section 5) also indicated that the formulated methodology in this work provides results which match well the input data and therefore is recommended to be applied.
7. CONCLUSION
- New expressions, providing very good results for the synthetic examples considered, were introduced to estimate permeability, skin factor and non-Newtonian fluid bank radius by means of TDS technique for a composite radial non-Newtonian/Newtonian reservoir. The applications did not take into account wellbore storage effects, and did not consider variable-rate injection tests. The methodology can be applied to falloff test.
ACKNOWLEDGEMENTS
The authors gratefully thanks Universidad Surcolombiana for providing support to the completion of this work.
REFERENCES
Ikoku, C. U. (1979). Practical Application of Non-Newtonian Transient Flow Analysis. Paper SPE 8351 presented at the SPE 64th Annual Technical Conference and Exhibition, Las Vegas, NV, Sept. 23-26. [ Links ]
Ikoku, C. U., & Ramey, H. J. Jr., (1979a). Transient Flow of Non-Newtonian Power-law fluids Through in Porous Media. US DOE Publication, (SAN),/1265-9. [ Links ]
Ikoku, C. U., & Ramey, H. J. Jr. (1979b). Transient Flow of Non-Newtonian Power-law fluids Through in Porous Media, Soc. Pet. Eng. J., 164-174. June. [ Links ]
Ikoku, C. U., & Ramey, H. J. Jr. (1979c). Wellbore Storage and Skin Effects During the Transient Flow of Non- Newtonian Power-law fluids Through in Porous Media. Soc. Pet. Eng. J., 164-174. [ Links ]
Katime-Meindl, I., & Tiab, D. (2001). Analysis of Pressure Transient Test of Non-Newtonian Fluids in Infinite Reservoir and in the Presence of a Single Linear Boundary by the Direct Synthesis Technique. Paper SPE 71587 prepared for presentation at the 2001 SPE Annual Technical Conference and Exhibition held in New Orleans, Louisiana, 30 Sept.-3 Oct. [ Links ]
Lund, O., & Ikoku, C. U. (1981). Pressure Transient Behavior of Non-Newtonian/Newtonian Fluid Composite Reservoirs. Soc. of Petrol. Eng. of AIME, 271-280, April. [ Links ]
Martínez, J. A., Escobar, F. H., & Montealegre-M., M. (2010). Numerical Solution for a Radial Composite Reservoir Model with a No-Newtonian/Newtonian Interface. Sent to revista Dyna to request publication. [ Links ]
Odeh, A. S., & Yang, H. T. (1979). Flow of non-Newtonian Power-Law Fluids Through in Porous Media, Soc. Pet. Eng. J., 155-163, June. [ Links ]
Savins, J. G. (1969). Non-Newtonian flow Through in Porous Media. Ind. Eng. Chem. 61 (10): 18-47. [ Links ]
Tiab, D. (1993). Analysis of Pressure and Pressure Derivative without Type-Curve Matching: 1- Skin and Wellbore Storage. J. of Petrol. Science and Eng., 12: 171-181. [ Links ]
Tiab, D. (1993). Analysis of Pressure and Pressure Derivative without Type-Curve Matching: 1- Skin and Wellbore Storage. Paper SPE 25423, Production Operations Symposium held in Oklahoma City, OK. 203-216. [ Links ]
Tiab, D. (1995). Analysis of Pressure Derivative without Type-Curve Matching: Vertically Fractured Wells in Closed Systems. J. of Petrol., Science and Eng., 11 (4): 323-333. [ Links ]
Vongvuthipornchai, S., & Raghavan, R. (1987). Well Test Analysis of Data Dominated by Storage and Skin: Non- Newtonian Power-Law Fluids. SPE Formation Evaluation, December, 618-628. [ Links ]