Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
CT&F - Ciencia, Tecnología y Futuro
Print version ISSN 0122-5383
C.T.F Cienc. Tecnol. Futuro vol.5 no.5 Bucaramanga July/Dec. 2014
OPTIMAL DESIGN FOR AN ETHANOL PLANT COMBINING FIRST AND SECOND-GENERATION TECHNOLOGIES
DISEÑO ÓPTIMO DE UNA PLANTA PARA LA OBTENCIÓN DE ETANOL COMBINANDO TECNOLOGÍAS DE PRIMERA Y SEGUNDA GENERACIÓN
DESENHO ÓTIMO DE UMA DESTILARIA PARA A OBTENÇÃO DE ETANOL COMBINANDO TECNOLOGIAS DE PRIMEIRA E SEGUNDA GERAÇÃO
Yailet Albernas-Carvajal1*, Gabriela Corsano2, Marlén Morales-Zamora1, Meilyn González-Cortés1, Ronaldo Santos-Herrero1 and Erenio González-Suárez1
1Universidad Central Marta Abreu de Las Villas, Santa Clara, Villa Clara, Cuba
2Instituto de Desarrollo y Diseño (INGAR), CONICET, Santa Fé, Argentina
e-mail: yailetac@uclv.edu.cu
* To whom correspondence should be addressed
How to cite: Albernas-Carvajal, Y., Corsano, G., Morales-Zamora, M., González-Cortés, M., Santos-Herrero, R. & González-Suárez, E. (2014). Optimal design for an ethanol plant combining first and second-generation technologies. CT&F - Ciencia, Tecnología y Futuro, 5(5), 97-120.
(Received: Apr. 04, 2014; Accepted: Dic. 26, 2014)
ABSTRACT
The synthesis and optimal design of batch plants is addressed in this study. It was applied to the technology of conventional ethanol production in a Cuban distillery using the product of enzymatic hydrolysis of pretreated bagasse as another sugared substrate, starting from laboratory results. The optimal configuration of stages, the number of units in each stage, the unit sizes and minimum total production cost are obtained from the global optimization model and the proposed superstructure. This global model is a mixed integer nonlinear programming (MINLP) formulation, which is represented and resolved by the Professional Software, General Algebraic Modeling System (GAMS) version 23.5 applying DICOPT Solver. Different scenarios are analyzed: attaching pretreatment and enzymatic hydrolysis of bagasse to a conventional distillery plant, selling ethanol, or selling the furfural as by-product if there is a guaranteed market. With this, an actual net present value (VNA) of USD 44´893 358.7 and 1.51 years of Payback Period (PP) are obtained.
Keywords: Bioethanol, Production, Optimization, Enzymatic hydrolysis, Models, Superstructure, Profitability.
RESUMEN
La síntesis y diseño óptimo de plantas discontinuas es abordada en el presente estudio; la cual fue aplicada a la tecnología de obtención de etanol convencional en una destilería cubana empleando el producto de la hidrólisis enzimática del bagazo pretratado como otro sustrato azucarado, partiendo de resultados de laboratorio. A partir del modelo global de optimización y la superestructura propuesta, se obtiene la configuración óptima de las etapas, el número de equipos en cada etapa, el volumen de los equipos y el mínimo costo total de producción. Dicho modelo global consiste en una formulación de programación matemática mixta entera no lineal (MINLP), la cual es representada y resuelta mediante el Software Profesional, General Algebraic Modeling System (GAMS) versión 23.5 con la aplicación del Solver DICOPT. Se analizan las posibles variantes a implementar que son en primer lugar las de acoplar la tecnología de pretratamiento e hidrólisis enzimática del bagazo a una destilería convencional vendiendo etanol y, en segundo lugar, vendiendo el co-producto furfural, si se garantiza un mercado para ello. Con lo anterior, se obtiene un Valor Actual Neto (VAN) de $ 44´893 358.7 USD y un período de recuperación de la inversión (PRD) de 1.51 años.
Palabras clave: Bioetanol, Producción, Optimización, Hidrólisis enzimática, Modelos, Superestructura, Rentabilidad.
RESUMO
A síntese e o desenho ótimo de usinas em desuso são abordados no presente estudo; os quais foram aplicados à tecnologia de obtenção de etanol convencional em uma destilaria cubana utilizando o produto da hidrólise enzimática do bagaço pré-tratado como outro substrato açucarado, partindo de resultados de laboratório. A partir do modelo global de otimização e da superestrutura proposta, é obtida a configuração ótima das etapas, o número de equipamentos em cada etapa, o volume dos equipamentos e o mínimo custo total de produção. Dito modelo global consiste em uma formulação de programação matemática mista inteira não linear (MINLP), a qual é representada e resolvida mediante o Software Profissional, General Algebraic Modeling System (GAMS) versão 23.5 com a aplicação do Solver DICOPT. São analisadas as possíveis variantes que devem ser implantadas que são em primeiro lugar as de acoplar a tecnologia de pré-tratamento e de hidrólise enzimática do bagaço a uma destilaria convencional vendendo etanol e, em segundo lugar, vendendo o coproduto furfural, se for garantido um mercado para o mesmo. Com o anterior, é obtido um Valor Atual Líquido (VAL) de $ 44´893 358.7 USD e um período de recuperação do investimento (PRI) de 1.51 anos.
Palavras-chave: Bioetanol, Produção, Otimização, Hidrólise enzimática, Models, Superestrutura, Rentabilidade.
1. INTRODUCTION
High economic dependence on fossil fuels and the devastating effects on climate and environment have made current research turn to the search for new sources of clean, renewable energies, such as biofuels (Morales, 2012; Limayem & Ricke, 2012). One of the technologies that has caught on in the search of alternatives for renewable fuels is second-generation ethanol, as stated by Carriquiry, Xu and Timilsina (2011). That is to say, based on lignocellulosic waste such as sugarcane bagasse, or the hydrolysates derived, according to Cardona, Quintero and Paz (2010). Also, the combination of first and second generation ethanol (Días et al., 2012; Ensinas et al., 2013), which according to Galdos et al. (2013) manages to include a new source of sugar-based products and, with them, the productions; in addition to the reduction of the negative impacts of first generation ethanol on global warming. Sugarcane bagasse is a solid residue of the extraction of juice from the cane to obtain sugar. In Cuba, it is highly available and has the economic advantage of not being rival to any food, as stated by Mesa et al. (2011a). According to reports by Hofsetz and Silva (2012), and Dantas, Legey and Mazzone (2013) for each ton of sugar cane, approximately 0.27 to 0.3 tons of bagasse are obtained; a portion of that bagasse is burned in the steam boilers of the sugar factories, but there is a considerable amount remaining that can be used to obtain second generation ethanol (Mesa et al., 2011b).
The use of sugars from lignocellulosic biomass (LCB), to produce bioethanol is an aspect that is currently highly discussed as stated by Noratiqah et al. (2013) and Albernas et al. (2014). To obtain glucose from the bagasse (or any lignocellulosic biomass in general), a set of previous operations is needed, known as pretreatment followed by enzymatic hydrolysis (Mussatto et al., 2010; Naik, Goud, Rout & Dalai, 2010; Ensinas et al., 2013). The purpose of pretreatment is to reduce or eliminate the physical and chemical barriers, such as the crystallinity of the cellulose, its acetyl groups of the hemicellulose and the bonds between hemicellulose and lignin, as stated by Pernalete et al. (2008), Naik et al. (2010) and Dantas et al. (2013). Also, it increases the porosity of the material and eliminates or decreases the presence of substances that interfere with or hinder enzymatic hydrolysis. Pretreatment methods refer to the solubilization and separation of one or more of the four components of the biomass (hemicellulose, cellulose, lignin and extracts) to make the remaining solid biomass more accessible to subsequent chemical or biological treatment (Domínguez, Álvarez, Granados & Hernández, 2012). The conversion of the cellulose fraction into glucose, which will be used in fermentation to produce ethanol, occurs in subsequent enzymatic hydrolysis. The efficiency of pretreatment depends on the enzyme accessing the cellulose more easily. The enzymatic hydrolysis of cellulose is based on the ability of certain microorganisms, (bacteria and fungi), to produce a set of extracellular enzymes capable of releasing D-glucose molecules that constitute it, by using cellulosic chains.
Previous studies have shown that this process has continuous and batch stages. The batch stages, such as enzymatic hydrolysis and fermentation, are considered critical, as they are unique in that their durations are long, where enzymatic hydrolysis fluctuates around 12 hours and fermentation around 24 hours, as stated by Mesa (2010) and Albernas et al. (2014). This fermentation only takes place in hexoses, in presence of the Saccharomyces cerevisiae DER CIEMAT Culture Collection No. 1701 yeast. According to Mesa (2010), 24 hours is the time to take the results of fermentation, in the conditions related to the working method at the industrial level in Cuba. This is a very important aspect in the analysis because it causes long waiting times in these two stages of the process, which affects the total time and causes that, for its continuity, a high number of units are needed in a first instance, which tends to affect profitability.
The Cuban distillery industry must look for new sources of raw materials that can be supplemented with molasses in the process of producing ethanol that will, at the same time, be competitive from the technical and economic standpoint.
Authors such as Mesa (2010), Mesa et al. (2011b), Morales, González, Mesa and Castro (2013) have shown that the technology of ethanol from bagasse presents drawbacks given the costs of some materials such as raw materials and the enzymes. And, although their costs have been reduced in recent years, it is still an economic issue as claimed by Ensinas et al. (2013), in addition to the cost of some of the essential equipment. As a result, to achieve profitability you have to seize the opportunity to obtain by-products provided by the particular process, as it is the case of furfural and lignin, which increase the profit of the process. An optimal design of the technology that will reduce process times is also necessary, taking into account the costs involved, as stated by Albernas (2014).
Dantas et al. (2013) claim that another aspect to take into account in order to achieve the economic viability of lignocellulosic ethanol using substrates, is the need for the development of efficient production methods including the fermentation of all sugars present in pretreatment and enzymatic hydrolysis. The fermentation of hexoses to ethanol is a consolidated process, and of a comprehensive domain when carried out by yeast or bacteria. However, most of the processes that have been carried out do not consider the fermentation of pentose because the yeasts commonly used for the fermentation of glucose (e.g. Saccharomyces cerevisiae) do not metabolize xylose (Dantas et al., 2013). To this effect, great efforts are being made to achieve processes with metabolic pathways capable of fermenting the pentose and xylose with satisfactory yields, as is the case of the Simultaneous Saccharification and Fermentation (SSF), as well as its expansion toward the Simultaneous Saccharification and Co-Fermentation (SSCF) (Hamelinck, Hooijdonk & Faaij, 2005). However, these processes are at a disadvantage because to achieve their economic viability, they require recombinant microorganisms consistent with biosecurity standards (Ramírez, 2001; Dantas et al., 2013).
The objective of this paper is the optimal design of an ethanol production plant combining first and second generation technologies using the superstructure methodology for batch processes; and analyzing application variants in Cuba based on the determination of the optimal times of involved operations, at the minimum production cost.
2. STATE OF THE ART
Description of the Ethanol Production Process Combining First and Second-Generation Ethanol Technologies
As previously explained, the process consists of four fundamental stages as stated by Hamelinck et al. (2005), Días et al. (2012) and Albernas et al. (2014): pretreatment, enzymatic hydrolysis, fermentation and distillation. The raw material used is the residual bagasse obtained from a sugar factory, stored with an average of 60% humidity.
The process consists of two stages of pretreatment of the bagasse, to increase the overall balance of subsequent conversion processes. The following occurs during pretreatment: the fractioning of the biomass into its main components (cellulose, hemicellulose and lignin), and the reduction of cellulose crystallinity and the increase in accessible surface area (Mesa, 2010; Morales, 2012; Dantas et al., 2013).
In acid pretreatment, a liquid rich in xylose is obtained, which has two key advantages: the elimination of a residual and the production of an added value product, which improves the economy of the process (Aguilar, Ramírez, Garrote & Vázquez, 2002; Albernas et al., 2012). To this end, the biomass is subjected to the action of a solution of dry fiber-based sulfuric acid at 1.25%, in the presence of steam at 175°C and 9 atm with a 1:4 kg/L solid liquid ratio; the residence time of this stage is 40 minutes, according to Mesa (2010). At this stage, high temperatures are required to achieve acceptable glucose outputs, which, in turn, lead to further decomposition of sugars from the hemicellulose, generating compounds such as furfural, as indicated by Lenihan et al. (2010) and Morales (2012).
Following the washing stage, a solid stream is also obtained with a high content of glucose in the form of cellulose, ready for a second phase of pretreatment which also has the action of steam, in which the solid is treated with a dry fiber-based solution of sodium hydroxide at 3% and ethanol at 30% v/v. At this stage, work is done at a temperature of 185°C, the solid-liquid ratio is 1:7 kg/L, residence time is 60 minutes and only 1% ethanol is lost with respect to dry fiber because it includes a system for the recovery thereof by condensation (Albernas et al., 2012).
Filtration is then carried out, in which a second solid mass is obtained with a small amount of lignin and a liquid current with a high content of this mass. The objective of pretreatment is to make the lignocellulosic biomass more susceptible to the following stage.
After that, the biomass is subjected to the enzymatic hydrolysis stage, through the action of the cellulase enzymes for 24-48 h. This stage is carried out at 45°C, using 30 FPU/g of cellulolytic enzymes Novozyme CellicRCTec2 and β-glucosidase NS50010. The volume of the second enzyme was 10% of the total volume enzyme to be used, as explained by Albernas (2014) and the xylanase employed is 20 FPU/g cellulases, working at a pH of 4.8 and 150 rpm. The glucose solution obtained experimentally by Mesa (2010) at this stage is 72.33 g/L. It is then filtered to use this glucose-rich fluid as a diluent agent of the final molasses obtained as a by-product in the production of sugar cane. These molasses have 520 g/L of fermentable sugars, thus incorporating the product of the enzymatic hydrolysis of the pretreated bagasse to the traditional process of ethanol production as another sugary current, which reduces the process' consumption of fresh water.
Subsequently, there is a pre-fermentation stage, whose fundamental objective is the growth of yeast that will later be used in alcoholic fermentation in the presence of nutrients and air that facilitate growth (Penín et al., 2010). After that, it goes on to the fermentation stage, at which the optimal sugar concentration is 120 g/L. At this stage, the yeast (Saccharomyces cerevisiae DER CIEMAT Culture Collection No. 1701), nutrients (urea and phosphate) (Albernas, Verelst, González & Pedraza, 2010) are added, and ethanol is produced at a concentration of 31.8 g/L, according to Mesa (2010) with a 12 hour duration, including 2 h for cleaning and disinfection (Penín et al., 2010). The fermented mash passes through five distillation columns in order to produce 500 hL of extrafine alcohol daily, with a 96.3ºGL quality. Figure 1 shows a flowchart of the process based on the studies of Mesa et al. (2011a).
The cellulosic ethanol process in itself only has the drawback that it is not profitable due to, among others, the large number of units required at key stages such as enzymatic hydrolysis and fermentation, which is why we need an appropriate design based on optimization techniques as discussed by Corsano, Aguirre, Iribarren and Montagna (2004), Corsano et al. (2006), Corsano, Montagna, Iribarren, and Aguirre (2006a), Corsano, Montagna, Iribarren and Aguirre (2007). This design used the superstructure technique, but the work was applied on ethanol production with a conventional method based on final molasses and other products such as torula yeast. The current study combines the first and second generation ethanol production processes, in addition to taking advantage of the by-products generated in the production of second-generation ethanol, which are furfural and lignin.
Approaches Discussed for the Problem of Synthesis, Design and Operation of Batch Processes
To design a batch plant, it is needed to determine the structure of the plant, the number of units to be used and their sizes. Several papers have been published in this regard using mixed integer nonlinear programming (MINLP) models, where the binary variables take into account different alternatives of the organizations of units at each stage. Papers have been presented where the different stages of the processes in question have been modeled using fixed times and size factors. There is extensive literature and previous work on synthesis and the design of batch stages described by fixed sizes and time factors: Knopf, Okos and Reklaitis (1982), Yeh and Reklaitis (1987), Ravemark and Rippin (1998) and Montagna et al. (2000). The first paper discusses the problem with algorithmic resolution procedures while the latter use MINLP. A first level of description of the representation of dependent units of these process variables consists of the use of algebraic models, which was first suggested by Salomone and Iribarren (1992) and applied later on a multiproduct batch plant problem in Pinto et al. (2001). This approach simultaneously optimizes the process variables and the decision variables of the plant.
A more detailed description of the representation of discontinuous stages requires modeling with differential equations. Barrera and Evans (1989) first, and then Salomone, Montagna and Iribarren (1994) suggested that the simultaneous optimization could be achieved by integrating the model of the batch plant with dynamic simulation models for the discontinuous units. An important aspect to note is that the approach presented by Salomone et al. (1994) suggests an algorithm whose sequence of resolution overcomes the problems of non-feasibility reported by Barrera and Evans (1989).
One way to incorporate the dynamic models of the units without losing the MINLP nature of the overall problem is to quantize the differential equations to turn them into algebraic restrictions of the program. This was the approach used by Bhatia and Biegler (1996), for examples of simple processes and Corsano (2005) in the problem of synthesis of complex networks of alcoholic fermentation, simultaneously obtaining the optimum number of units, operating mode and their sizes. The same author gets the design variables of the discontinuous stages such as size factors, processing times and operating costs, to be calculated as a function of process variables, which was also addressed by Fumero, Montagna and Corsano (2012). Corsano et al. (2004) shows a model that simultaneously obtains the optimal synthesis, design and operation of a multipurpose sequential plant with mixed campaigns, where the task sequencing restrictions are taken into account in the global model. The structural considerations of the plant, such as the number of units of a stage, are resolved simultaneously in the model formulated as an NLP problem.
Corsano (2005), solves the synthesis problem by using at the same time the equations of the fermenter model and their interconnection as a non-linear programming (NLP) problem. This is something new in this area because an optimal design is obtained based on a complete model of fermenter networks.
While it is true that in these analyses, using constant size and time factors requires the setting of decision variables of the process units, no studies have been reported combining -in the same global optimization model-, the use of the time factors with the phenomenological models of the stages involved in the design; which is applied in this paper.
Formulation of the Global Model and the Superstructure
According to the points raised by Corsano (2005), the superstructure of the process, applied to processes with batch stages, leads to the optimal design of the process stages. This approach schematically considers all the possible configurations of a batch plant in the same model and includes characteristics of each of the stages, through the formulation of models, whether they are phenomenological and/or statistical, and size factors of the stages, in order to perform the synthesis and the optimal design of the bioethanol production process using the product of enzymatic hydrolysis of the pretreated bagasse, thus minimizing production cost.
The main product of these operations is known as ethanol and must meet a demand Q of 500 hL/d in the time horizon TH of 1 year. For the processing of the stages, p operations are required. Each operation is completed in certain stages j. For each of the production operations p, there is an upper bound Cp on the number of stages to be considered for this operation, see Figure 2. This allows each operation to vary the number of stages to be considered; therefore, for each operation p, there is a set of stages ranging from 1 to Cp, whose solution must be determined as a solution to the optimization problem. The stages j,p,α, existing in the alternative αp of operation p, can vary between 1 and Cp. For each alternative αp, the number of stages is predetermined.
For each operation p, alternatives ap = 1, …, Ap are defined. Each of the alternatives αp existing in operation p, should be characterized, which involves the definition of the following elements:
- The number of stages to be included in the alternative.
- The last stage included in the alternative (basic data for the connection between successive operations).
- The number of duplicated in phase and/or out of phase units for each of the stages included in the alternative (See Figure 3).
Once these elements have been defined, the superstructure for NLP is proposed, which is defined by the designer based on his experience in the process in question. Based on the methodology proposed by Corsano et al. (2006) and applied in Corsano et al. (2007); and by Albernas (2014) a certain operation with Cp = 2 stages, indicates than any alternative used in this operation can have up to 2 stages. Each of these stages has structural options based on the duplication of the units included therein. Each of these options is predetermined in each alternative αp (Albernas, 2014; Albernas et al., 2014).
One option for the configuration of the operation is the duplication of stages in series. It is assumed that there is a determined cycle time that is a variable of the problem for that operation, which is the longest of the time of all the stages involved therein. Therefore, all the units that require a shorter operating time have a standby or idle time.
The objective function to be proposed takes into account the costs of the units involved in each of the operations, as well as the operating costs of each.
Where Vp, α, j is the unit size j (volume) in alternative a for operation p.
The volumes of the various units are listed in Equation 1, through the design equations and models that describe each of the stages.
The cost of the units is calculated based on coefficients αp and βp used in this type of problems according to Biegler, Grossmann and Westerberg (1998); Seider, Seader and Lewin (2003); Corsano (2005), where αp is the investment cost of the equipment and βp is its cost exponent. These coefficients are assumed to be the same for the stages of all the alternatives within an operation.
Mp,α,j and Gp,α,j are the number of duplicated out of phase and in phase units respectively. For stage j, in alternative α for operation p, OC represents the operating costs that depend on how the operation is carried out (Albernas et al., 2014).
The above expression considers all stages j of all the existing alternatives for operation p. The optimum alternative is identified in the solution as the one that has a unit size other than zero.
Model Constraints
The required demand must be covered, for which Production Rate (PR) indicated by Albernas, González, Pedraza and González (2011) is used, which comes from:
The Final Product is Obtained at the Last Stage of the Last Operation
The sum of what is produced through all the alternatives must meet the requirements established for the plant.
Where: plαst is the last operation.
For this operation, the productions PRlαst are joined in each of the alternatives available, which are given by:
QPlαst is the quantity produced in alternative αp in the last operation, TC is the plant's cycle time.
The model includes all the alternatives simultaneously, and the target function will lead to the selection of only the best one. For this alternative, the TC will make physical sense, whereas for the others, it will be meaningless.
The total produced must be at least equal to the plant requirement and the quantity to be produced will be just PR, in order to try to minimize the costs. This will be achieved by using one of the alternatives in operation Plαst.
The plant's cycle time, based on the Zero Wait (ZW) transfer policy, is determined by the longest of all times required in the stages used at the plant.
Tpαj is the operation time of the unit of stage j for alternative α in operation p. This value is an operation value and it is calculated by the model that describes the operation as follows:
Where Mpαj is the number of duplicated out of phase units for stage j in alternative α for operation p.
Connection Balances Between Stages
The connection balances must be established between successive stages of each alternative of an operation.  and
and  are the volume of the batch entering and exiting each unit of stage jpα in operation p, we have:
are the volume of the batch entering and exiting each unit of stage jpα in operation p, we have:
If various materials are handled, this type of connection constraint must be established for each of them.
Connection Balances Between Operations
To ensure the connection between successive operations, the last stage of one operation must be placed in contact with the first stage of the following operation as follows:
This indicates that the total obtained in the last stage jlast of all the alternatives of operation p, must be equal to all the material entering the first stage of the following operation. The values of Bpaj and Tpaj used must be characterized suing the proper equations.
Number of Units by Stages
As part of defining the superstructure by stages, the designer suggests several alternatives that include a certain number of units, which serves as a model limit.
Minimum and Maximum Capacities of the Units
The possible minimum and maximum capacities of the units are an element that is also established like the dimensions, in accordance with the results of previous studies and similar equipment installed at the industrial level.
The optimal configuration of the operations that includes the number of units in each operation and their volume will be obtained as a response to variables to the global model, such as the borderline cycle time, the end time of each operation, and the total cost of annual production.
3. APPLICATION OF THE SUPERSTRUCTURE
The main product of these operations is ethanol and it must satisfy a demand Q of 500 hL/d of ethanol in time horizon TH of 1 year. The general model optimizes the design of stages in the operations; in this case, the ethanol production process, thus minimizing costs (Albernas et al., 2014).
Superstructure Model for Acid, Alkaline Pretreatment and Enzymatic Hydrolysis
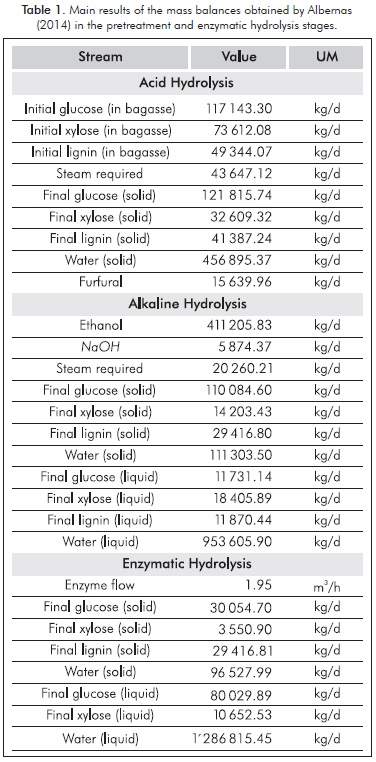
For the analysis of the superstructure of the pretreatment stages also studied by Reales-Alfaro et al. (2013), and enzymatic hydrolysis, it is assumed that there is no difficulty with the delivery of the essential raw material (bagasse). That is to say, there are no waiting times in reference to the raw material, so the logistics and the uncertainty are not considered in the formulation of the problem. Table 1 shows the fundamental results of the mass balances obtained by Albernas (2014), which were taken based on this study.
To propose the superstructure model of the pretreatment and enzymatic hydrolysis stages, the associated size factor concept is applied for each of the stages. (see Table 2).
The input quantities at each stage are taken from the mass balances developed by Albernas (2014) for which the quantity of hydrolysate from the enzymatic hydrolysis is taken as a final product, because it is the product from the sections of bagasse processing in general, later used in the fermentation stage at a value of 1'377 497.87 kg/d.
With these size factors, in order to calculate the volumes of the unit, the equation that relates the size factor with the batch size was used.
Where batch size (TBi) is 5.28. This is determined based on the determined ratio of balances between the product of the enzymatic hydrolysate and the initial bagasse used, affected by the cycle time of the three operations.
The cycle time for the three operations is calculated considering that they are operations that operate in parallel out of phase, as follows:
Where τj is the processing time in stage j, NPj, j = 1..M stages.
To determine processing times, the times involved in the different operations of each process were taken into account, as shown in Table 3, based on estimates of the laboratory results, combined with the experience with units of similar characteristics. In the case of reaction time in pretreatment, the equations to calculate time based on the models of rate expressions of the interest components were used, and in the case of enzymatic hydrolysis, it was also calculated based on the experimental results developed by Albernas (2014), whose fundamental results are listed in Table 1. In the case of enzymatic hydrolysis, the strategy of simultaneously loading and heating, as well as cooling and unloading, was applied.
Superstructure Model for Pre-Fermentation and Ethanol Fermentation Operations
Fermentation for bioethanol production consists of two operations, which are biomass fermentation or pre-fermentation and ethanol fermentation. For these stages, the mass balance models are described by the following differential equations according to Chekhova, Barton and Górak (2000) and Nielsen, Villadsen and Liden (2003) which were also applied by Albernas et al. (2014):
Where, Equations 11 - 13 and 15 are described for the pre-fermentation operation, and Equations 14 for fermentation, because the first operation only produces biomass. Subindex p refers to the pre-fermentation or fermentation operations (p=4 and p=5 respectively), while α refers to the alternative of the selected configuration for the superstructure (number of duplicated out of phase units for each stage), α € Ap, Ap are the different alternatives for p. X is the biomass concentration (kg/m3), S is the substrate concentration (kg/m3), Xd is the non-active biomass concentration (kg/m3) and E is the ethanol concentration (kg/m3), µ is the specific growth rate. These are all variables of the problem, u represents the death rate of the microorganisms, Ye is the ethanol yield coefficient and ks is the substrate saturation constant. Those are the parameters of the model. Yx is the biomass yield and it is a function of the substrates used in feeding the pre-fermenter for the fermenters and a constant for the alcoholic fermentation operation.
In all the stages of the two operations, an extra feed can be added to the one coming from the previous stage. This feed consists of a mixture of sugared substrates formed by B molasses, an enzymatic hydrolysate from the pretreated bagasse and water, which can be used to dilute the molasses as illustrated in the block diagram in Figure 1. Retention time in filters between fermentation and distillation is not taken into consideration because they operate continuously (Albernas et al., 2010).
As proposed in the global model, the goal is to minimize total annual costs, which are proposed as annual investment costs added to an operating cost (consisting of the cost of substrates, nutrients and other materials involved) in correspondence with Seider et al. (2003).
Where, Cαnn is a constant that annualizes investment cost, CCF is the depreciation of the units and Cf represents the cost per m3 of material involved f used in feeding unit j of alternative αp. TH is the time horizon (1 year), which is divided by cycle- time TC to express this annual cost. The values of the cost exponents α and β were taken from Table 16.32 of Nielsen et al. (2003) where the volumes of the equations are expressed in the units listed in Table 4.
Superstructure for the Involved Operations
In the superstructure for the acid, alkaline pretreatment and enzymatic hydrolysis operations, there are three operations (p = 3). For the first operation, acid pretreatment (p = 1), a stage (C1 = 1) is suggested, including three alternatives (a1 = 3) which are taken into account at this stage. The first presents the out of phase triplication in parallel of this stage; the second one presents four out of phase units in parallel of this stage, and the third one presents five units operating in the same way.
The second operation, alkaline pretreatment (p = 2), proposes a stage (C2 = 1). This includes three alternatives (a2 = 3), which are taken into account at this stage. The first presents six out of phase units in parallel of this stage; the second one presents eight out of phase units in parallel of this stage, and the third one has ten units operating in the same way.
In the third operation, enzymatic hydrolysis (p = 3), the number of units suggested is high given the processing time for this stage, so a stage (C3 = 1) is proposed. This includes three alternatives (a3 = 3), which are taken into account at this stage. The first presents 28 out of phase units in parallel of this stage; the second presents 30 out of phase units in parallel of this stage, and the third presents 32 units operating in the same way.
The superstructure for the pre-fermentation and fermentation operations consists of two operations following the previous one (p = 4, 5). For the pre-fermentation operation (p = 4), a stage (C4 = 1) is proposed, so any alternative can have one stage at most. This includes three alternatives (a4 = 3), which are taken into account at this stage. In the first, there is a single stage, while the second is the out of phase parallel duplication of this stage, and the third is the out of phase parallel triplication of this stage.
For the fermentation operation (p = 5), three alternatives (a5 = 3) of just one stage (C5 = 1) are considered. In this case, the first alternative consists of placing 8 out of phase units in parallel of this stage; the second alternative consists of placing 10 out of phase units in parallel of this stage, and the last consists of placing 12 out of phase units in parallel of this stage.
Table 5 summarizes the number of units involved in each of the operations, which are proposed based on the estimates of the lab results (pretreatment and enzymatic hydrolysis) and the existing units in Cuban distilleries with similar capabilities (pre-fermentation and fermentation).
In all the operations of the three alternatives, no in-phase units are considered due to the characteristics of these operations. Therefore, for the model, it is G = 1. The differential Equations 11 - 15 are discretized using the trapezoidal method, which is an explicit one-step method that has the special property of stability proposed by Atkinson (1989). 30 nodes were taken in the discretization, so the length of the step in each case was equal to the operating time divided by 30. The stability of this method for the pre-fermentation and fermentation operations was verified in the work by Corsano et al. (2004). The algebraic equations resulting from the discretization were embedded in the global model, which is formulated and solved in the Professional Software, General Algebraic Modeling System, (GAMS) v. 23.5, by applying Solver CONOPT specialized in NLP (Albernas et al., 2014).
Parameters Considered in the Optimization of the Ethanol Production Process
For the models, a time horizon of 7 200 h.year-1 (300 days.year-1) was taken along with a fixed ethanol production rate of 500 hL.days-1. Fermentation substrate is understood as the mixture of sugars with six carbon atoms (glucose) contained in the product of the enzymatic hydrolysis of the pretreated bagasse and molasses, because the strain of Saccharomyces cerevisiae DER CIEMAT Culture Collection No. 1701, does not have a dual metabolism, so it only ferments sugars with six carbon atoms. Table 6 shows some of the main parameters used in the model for the pre-fermentation and fermentation operations.
4. RESULTS AND DISCUSSION
Estimate of Optimal Enzymatic Hydrolysis Time
As reflected in Table 3, enzymatic hydrolysis reaction time is a crucial point because it is one of the critical stages of the process due to its length; therefore, obtaining a minimum time should be analyzed in order to obtain a proper level of Total Reducing Sugars (TRS) to ensure the efficiency of this stage. This study shows that at 24 h, 45.56 g/L are produced; however, at 48 h, the maximum formation of TRS is 58 g/L. Therefore, if 24 h is established as the final point of analysis, 12.44 g/L will not be produced by avoiding a waiting time of 24 h.
With this in mind, the global model GAMS is implemented with variations in the reaction times of enzymatic hydrolysis in accordance with those established in Table 7. The TRS values listed in this table were obtained by experiment by Albernas (2014) and they are in line with those reported by Mesa (2010).
Based thereon, 5 different runs are obtained with different designs in each of the cases. Therefore, 4 alternatives are studied.
Alternative 1: purchase all the equipment and sell ethanol.
Alternative 2: attach it to a distillery and sell ethanol (pre-fermentation and fermentation units are not purchased).
Alternative 3: purchase all the equipment and sell ethanol and furfural.
Alternative 4: attach it to a distillery and sell ethanol and furfural (pre-fermentation and fermentation units are not purchased).
The result is 4 alternatives with 5 design operations each; therefore, in each case, an economic feasibility study was conducted with the results using the factorial methodology of Peters and Timmerhaus (1968), to find the optimum enzymatic hydrolysis time in each of them.
The first variant of purchasing all the equipment and selling only ethanol is analyzed as illustrated in Figure 4, which shows the Payback Period (PP) expressed in years vs. the enzymatic hydrolysis time expressed in hours. In this variant, the optimum overall time is 24 h and it is recovered in 13 years, which is where the overall minimum occurs. Since this is not economically feasible, this alternative is discarded.
In the investment process, the equipment corresponding to the pre-fermentation and fermentation stages is not purchased. This happens because there is not enough molasses for the entire year, based on the analysis of using the product of the enzymatic hydrolysis of the pre-treated bagasse obtained, along with the molasses of a distillery, and completing its capacity. The alternative of attaching to a distillery would imply that the enzymatic hydrolysis stage would have a length of 24 h and the total investment would be recovered in 4 years, Figure 5.
Based on the mixture study conducted by Morales (2012), we used the 50% and 50% substrate mixture that yielded the most favorable results in regards to the alcohol strength obtained in the ferment based on the combinations of substrates used: an average alcohol strength of 5.07% of the ferment. According to Colectivo de Autores (1983), Gálvez (1988) and Fabelo (1998), this value is in the order of those obtained for fermentations (4.0-6.5% ethanol) prior to the ethanol distillation stage. The model obtained is:
Where, Y1 is the alcohol percentage obtained, X1 and X2 are the percentage of molasses and the product of enzymatic hydrolysis of the pre-treated bagasse. Although the correlation coefficient value obtained of 86.39% is not a high value from the experimental standpoint, according to González (2005), it is within an accepted range when it comes to results to be applied at the industrial level, which is above 85%. This variant is the first most attractive to be implemented.
An analysis of the production of the by-product (furfural), together with bioethanol, shows that for the case of purchasing all the equipment, the minimum payback period (PP) is 3.1 years, at 5 h (See Figure 6). This implies that what is important in this case is not the production of sugars to produce bioethanol, because at 5 h, only 24.59 g/L of TRS has been obtained; that is to say, this case places greater importance on the production of the by-product, so this alternative is not attractive for implementation.
A final analysis of the possibility of using the installed capacity in pre-fermentation and fermentation by attaching it to a distillery and also producing furfural, yields greater use of the bagasse for the production of sugars, leading to the recovery of the investment in 1.5 years, which is the best solution as illustrated in Figure 7 and optimum time is 18 h.
The most attractive variant to be applied is that of obtaining bioethanol attached to a distillery and using the product of the enzymatic hydrolysis of the pre-treated bagasse as a complementary substrate to satisfy the lack of molasses thereof and upon implementing it. If there is a secure market for the furfural, it would complete the investment in this sense, taking into account the last variant analyzed.
Optimum Results Obtained by Implementation in GAMS
One measure of the robustness of the model implemented to achieve the optimum design can be obtained by analyzing Table 8, which shows that at a low execution time, 0.016 seconds, 758 equations can be processed with 785 variables and 2650 non-linear elements.
For the first alternative selected based on the analysis of profitability upon attaching it to a distillery and selling ethanol, the results shown in Tables 9 and 10 are obtained.
The numbers and volumes of the units are calculated in full accordance with the analyses conducted previously and with the results of some authors, such as Sammak, Rousta, Tabari and Yazdanian (2007). In the case of the pre-fermentation and fermentation stages, they are consistent with the existing units in the distilleries installed in Cuba with similar capabilities. The duration times of the stages are also within those calculated by Albernas (2014).
It is important to point out that this study is a preliminary Class 4 assessment according to the A.A.C.E., with an accuracy between 70 and 85%, so new investments are those related to the enzymatic hydrolysis and pretreatment stages. As addressed earlier, these were taken based on the cost exponents explained by Nielsen et al. (2003) with the values listed in Table 4. The rest of the items related to investments were taken from estimates using the Peters and Timmerhaus (1968) methodology.
The investment values were updated in the GAMS program using the rate reported by the Chemical Engineering journal for the year 2013, which is 567.3 (Bailey, 2014). These evaluations would involve adding the enzymatic hydrolysis and pretreatment stages to an existing distillery, so these are the stages that are considered a new investment and require new land adjacent to said distillery. The fermentation and distillation stages are not taken into account in the calculation of the investment, because the existing ones are used; thus confirming that the number of units and volumes obtained in pre-fermentation and fermentation are similar to those existing at the current plant.
When attaching the second-generation technology under analysis to a distillery installed with first generation technology and selling only ethanol, savings will be made on the expenses related to the investment of the pre-fermentation and fermentation stages because they already exist and are installed therein. From the economic standpoint, this has a positive effect with a profit of USD 4´205 184 per year, recovering the investment related with the second generation ethanol in 4 years. This setup takes advantage of the possibility of using an additional sugared substrate that will mitigate the lack of molasses suffered by some of the Cuban distilleries at a certain time of year, which is of great importance from the technical and economic standpoint. This also makes it possible to have the ethanol technology in Cuba using products from the hydrolysate of bagasse that remains as a residual and is not used in cogeneration.
The second variant, which appeared to be attractive for use in the prior analyses, consisted of attaching it to a distillery and selling ethanol and furfural, which, as expected, has the economic results illustrated in Table 11, from selling a product with high value-added. Production and investment to produce furfural was estimated based on the results obtained by Morales (2012).
All the information necessary to calculate the costs was taken from conventional Cuban distilleries that are currently in operation, as discussed by Albernas (2014). The ethanol sale price was taken from the current Cuban distilleries and is consistent with Ensinas et al. (2013), as well as in the ranges reported by Trinder (2014). For the economic evaluation, an interest rate of 15% was used and the results displayed are taken from the second year in which the investment was executed. However, this alternative has a very high recovery rate of 1.51 years, due to the possibility of selling a by-product such as furfural, which is easily obtained in addition to the acid pretreatment of the bagasse in second-generation technology. The investment to do so is considered minimal (USD 65 195.72) in relation to the value of the product. The fact that it can be quoted at USD 1.80/kg makes the value of the production for this concept high (USD 8´445 578.4 per year), with an internal rate of return that can be considered high at 84.7%. This variant leads to a profit of USD 10´969 410.2 per year, but bear in mind that the possibility of the implementation of this variant is subject to ensuring a secure market for the by-product (furfural); otherwise, there would be no sense in undertaking such an investment.
Table 12 below provides a detailed breakdown of the estimated costs related to the investment and installation of each of the variants under analysis.
Based on the results obtained with the optimal superstructure, the resulting superstructure was built in a Gantt Chart as illustrated in Figure 8. All the stages operate based on the zero-waiting policy except for enzymatic hydrolysis, because storage tanks must be put in place for the hydrolysate to store the content of a hydrolyzer before going on to fermentation, in order to make the equipment prior to this stage smaller. In this tank, there is a maximum wait equal to the process cycle time, which is 2.5 h. This time does not affect the quality of the enzymatic hydrolysate.
In this case, assuming the maximum wait time, the total time of the process is 66.8 h ≈ 2.8 days, which is the delay in obtaining the first complete batch of ferment. Once the plant is on system, a new fermenter will be ready every 2.5 h to be distilled, thus ensuring the continuity of the distillation stage.
5. CONCLUSIONS
- The first optimal variant to be introduced is that of obtaining bioethanol attached to a distillery and using the product of the enzymatic hydrolysis of the pre-treated bagasse as a complementary substrate to satisfy the lack of its molasses. This alternative offers a VNA of USD 12'170992.17 and a PP of 4 years. The second optimal variant to be implemented is that of obtaining bioethanol attached to a distillery and selling ethanol and furfural. This would require a total investment of USD 1´220493.32 for a profit of USD 10´969410.2 per year, a VNA of USD 44´893358.7 and a PP of 1.51 years.
- The combined analysis of the mathematical model with the dynamic profitability indicators showed that the optimum enzymatic hydrolysis time in the alternative of attaching it to the distillery and selling ethanol is 24 h, obtaining 45.56 g/L of hydrolysate. In the alternative of obtaining bioethanol attached to a distillery selling ethanol and furfural, it is 18 h obtaining 40.56 g/L of the product of the enzymatic hydrolysis from the pretreated bagasse.
- The determined optimal configuration considers 3 acid hydrolyzers of 99 m3, 6 alkaline hydrolyzers of 57 m3, 28 enzymatic hydrolyzers of 143 m3, two pre-fermenters of 10 m3 and 12 fermenters of 85 m3, all operating out of phase in parallel.
ACKNOWLEDGEMENTS
The authors appreciate the support from Ministerio de Ciencia, Tecnología e Innovación Productiva (MINCYT) from Argentina and Ministerio de Ciencia, Tecnología y Medio Ambiente (CITMA) from Cuba.
REFERENCES
Aguilar, R., Ramírez, J. A., Garrote, G. & Vázquez, M. (2002). Kinetic study of the acid hydrolysis of sugar cane bagasse. J. Food Eng., 55(4), 309-318. [ Links ]
Albernas, Y. (2014). Procedimiento para la síntesis y el diseño óptimo de plantas discontinuas de obtención de bioetanol empleando bagazo de caña de azúcar. Tesis de Doctorado, Facultad de Química y Farmacia, Departamento de Ingeniería Química, Universidad Central Marta Abreu de Las Villas, Santa Clara. Cuba. 112pp. [ Links ]
Albernas, Y., Corsano, G., Kafarov, V., González, M. & González, E. (2014). Optimal design of pre-fermentation and fermentation stages applying nonlinear programming. Energ. Convers. Manage., 87: 1195-1201. [ Links ]
Albernas, Y., González, M., Pedraza, J. & González, E. (2011). Visión global sobre la planificación de procesos discontinuos. Afinidad, 68(553), 203-209. [ Links ]
Albernas, Y., Mesa, L., González, E., González, M., Díaz, M. & Castro, E. (2012). Evaluación económica de las alternativas de pretratamiento para la producción de etanol a partir de bagazo. Centro Azúcar, 39(2), 58-64. [ Links ]
Albernas, Y., Verelst, H., González, E. & Pedraza, J. (2010). Simulation of the batch fermentation stage in the process to obtain ethanol from final molasse. Chem. Eng. Trans., 21: 931-936. [ Links ]
Atkinson, K. E. (1989). An introduction to numerical analysis. Second Edition. New York: John Wiley & Sons. [ Links ]
Bailey, M. P. (2014). Economics Indicator. Chemical Engineering, 121(4). [Consulted: April 2014]. Available at: <http://www.chemeng.queensu.ca/courses/CHEE332/files/CEPCI_2014.pdf> [ Links ].
Barrera, M. D. & Evans, L. B. (1989). Optimal design and operation of batch processes. Chem. Eng. Commun., 82(1), 45-66. [ Links ]
Bhatia, T. K. & Biegler, L. T. (1996). Dynamic optimization in the design and scheduling of multiproduct batch plants. Ind. Eng. Chem. Res., 35(7), 2234-2246. [ Links ]
Biegler, L. T., Grossmann, I. E. & Westerberg, A. W. (1998). Systematic methods of chemical process design. New Jersey: Prentice Hall. [ Links ]
Caicedo, A. A. (1999). Tutorial de biorreactores con simulación de bioprocesos. Tesis de pregrado, Facultad de Ingeniería, Departamento de Ingeniería Química. Universidad Nacional de Colombia, Bogotá, Colombia. 135pp. [ Links ]
Cardona, C. A., Quintero, J. A. & Paz, I. C. (2010). Production of bioethanol from sugarcane bagasse: Status and perspectives. Bioresourse Technology, 101(13), 4754-4766. [ Links ]
Carriquiry, M. A., Du, X. & Timilsina, G. R. (2011). Second generation biofuels: Economics and policies. Energy Policy, 39(7), 4222-4234. [ Links ]
Chekhova, E., Barton, P. I. & Górak, A. (2000). Optimal operation processes of discrete-continuous biochemical processes. Comput. Chem. Eng., 24: 1167-1173. [ Links ]
Colectivo_De_Autores (1983). Manual de operación para la producción de alcohol y levadura Saccharomyces. Santa Clara: Destilería Heriberto Duquesne. Ministerio de la Industria Azucarera. Dirección de Derivados. [ Links ]
Corsano, G. (2005). Estrategia en el diseño óptimo de plantas de procesos batch de la industria alimenticia integradas a procesos fermentativos. Tesis de Doctorado, Facultad de Ingeniería y Ciencias Hídricas, Universidad Nacional del Litoral, Santa Fé, Argentina. 161pp. [ Links ]
Corsano, G., Aguirre, P. A., Iribarren, O. A. & Montagna, J.M. (2004). Batch fermentation networks model for optimal synthesis, design and operation. Ind. Eng. Chem. Res., 43(15), 4211-4219. [ Links ]
Corsano, G., Iribarren, O., Montagna, J. M., Aguirre, P. & González, E. (2006). Economic tradeoffs involved in the design of fermentations processes with environmental constraints. Chem. Eng. Res. Des., 84(10), 932-942. [ Links ]
Corsano, G., Montagna, J. M., Iribarren, O. & Aguirre, P. (2006a). Design and operation issues using NLP superstructure modeling. Appl. Math. Model., 30(9), 974-992. [ Links ]
Corsano, G., Montagna, J., Iribarren, O. & Aguirre, P. (2007). Heuristic method for the optimal synthesis and design of batch plants considering mixed product campaigns. Ind. Eng. Chem. Res., 46(9), 2769-2780. [ Links ]
Dantas, G. A., Legey, L. F. L. & Mazzone, A. (2013). Energy from sugarcane bagasse in Brazil: An assessment of the productivity and cost of different technological routes. Renew. Sust. Energ. Rev., 21: 356-364. [ Links ]
Días, M. O. S., Junqueira, T. L., Jesus, C. D. F., Rossell, C. E. V., Filho, R. M. & Bonomi, A. (2012). Improving second generation ethanol production through optimization of first generation production process from sugarcane. Energy, 43(1), 246-252. [ Links ]
Domínguez, M., Álvarez, A., Granados, M. & Hernández, F. (2012). Estudio de la cinética del pretratamiento e hidrólisis ácida del bagazo de caña de azúcar. Rev. Iberoam. Polím., 13(4), 200-211. [ Links ]
Ensinas, A. V., Codina, V., Marechal, F., Albarelli, J. & Silva, M. A. (2013). Thermo-economic optimization of integrated first and second generation sugarcane ethanol plant. Chem. Eng. Trans., 35: 523-528. [ Links ]
Fabelo, J. A. (1998). Estudio de la etapa de fermentación alcohólica utilizando diferentes sustratos. Tesis de Doctorado, Facultad de Química y Farmacia, Departamento de Ingeniería Química, Universidad Central Marta Abreu de Las Villas, Santa Clara, Cuba. 124pp. [ Links ]
Fumero, Y., Montagna, J. M. & Corsano, G. (2012). Simultaneous design and scheduling of a semicontinuous/batch plant for ethanol and derivatives production. Comput. Chem. Eng., 36(10), 342-357. [ Links ]
Galdos, M., Cavalett, O., Seabra, J. E. A., Horta, L. A. & Bonomi, A. (2013). Trends in global warming and human health impacts related to Brazilian sugarcane ethanol production considering black carbon emisions. Applied Energy, 104: 576-582. [ Links ]
Gálvez, L. (1988). Manual de los derivados de la caña de azúcar. Colección 1ra Edición. México: GEPLACEA. [ Links ]
González, E. (2005). Los estudios previos para minimizar la incertidumbre en la absorción (asimilación) de tecnologías que emplean la biomasa como fuente de productos químicos y energía. Buenos Aires: CYTED, WorldPress. [ Links ]
Hamelinck, C. N., Hooijdonk, G. & Faaij, A. P. C. (2005). Ethanol form lignocelullosic biomass: techno-economic performance in short-, middle- and long-term. Biomass and Bioenergy, 28(4), 384-410. [ Links ]
Hofsetz, K. & Silva, M. A. (2012). Brazilian sugarcane bagasse: Energy and non-energy consumption. Biomass and Bioenergy, 46: 564-573. [ Links ]
Knopf, F. C., Okos, M. R. & Reklaitis, G. V. (1982). Optimal design of batch/semicontinuous processes. Ind. Eng. Chem. Process Des. Dev., 21(1), 79-86. [ Links ]
Lenihan, P., Orozco, A., O´Neill, E., Ahmad, M. N. M., Rooney, D. W. & Walker, G. M. (2010). Dilute acid hydrolysis of lignocellulosic biomass. Chem. Eng. J., 156(2), 395-403. [ Links ]
Limayem, A. & Ricke, S. C. (2012). Lignocellulosic biomass for bioethanol production: Current perspectives, potential issues and future prospects. Prog. Energy Combust. Sci., 38(4), 449-467. [ Links ]
Mesa, L. (2010). Estrategia investigativa para la tecnología de obtención de etanol y coproductos del bagazo de la caña de azúcar. Tesis de Doctorado, Facultad de Química y Farmacia, Departamento de Ingeniería Química, Universidad Central Marta Abreu de Las Villas, Santa Clara. Cuba. 128pp. [ Links ]
Mesa, L., González, E., Cara, C., González, M., Castro, E. & Mussatto, S. I. (2011a). The effect of organosolv pretreatment variables on enzymatic hydrolysis of sugarcane bagasse. Chem. Eng. J., 168(3), 1157-1162. [ Links ]
Mesa, L., González, E., Romero, I., Ruiz, E., Cara, C. & Castro, E. (2011b). Comparison of process configurations for ethanol production from two-step pretreated sugarcane bagasse. Chem. Eng. J., 175: 185-191. [ Links ]
Montagna, J. M., Vecchietti, A. R., Iribarren, O. A., Pinto, J. M. & Asenjo, J. A. (2000). Optimal design of protein production plants with time and size factor process models. Biotechnol. Prog., 16(2), 228-237. [ Links ]
Morales, M. (2012). Estrategia para la reconversión de una industria integrada de azúcar y derivados para la producción de etanol y coproductos a partir del bagazo. Tesis de Doctorado, Facultad de Química y Farmacia, Departamento de Ingeniería Química, Universidad Central Marta Abreu de Las Villas, Santa Clara, Cuba. 115pp. [ Links ]
Morales, M., González, E., Mesa, L. & Castro, E. (2013). Estrategia de reconversión de la industria diversificada de la caña de azúcar para la producción conjunta de bioetanol y coproductos. Rev. Fac. Ing. Univ. Antioquia, 66: 189-198. [ Links ]
Mussatto, S. I., Dragone, G., Guimarães, P. M., Silva, J. P., Carneiro, L. M., Roberto, I. C., Vicente, A., Domingues, L. & Teixeira, J. A. (2010). Technological trends, global market, and challenges of bio-ethanol production. Biotechnol. Adv., 28(6), 817-830. [ Links ]
Naik, S. N., Goud, V. V., Rout, P. K. & Dalai, A. K. (2010). Production of first and second generation biofuels: A comprehensive review. Renew. Sust. Energ. Rev., 14(2), 578-597. [ Links ]
Nielsen, J., Villadsen, J. & Liden, G. (2003). Bioreaction engineering principles. Second Edition. New York: Kluwer Academic/Plenum Publisher. [ Links ]
Noratiqah, K., Madihah, M. S., Siti, B., Shaza, M., Suraini, A. & Kamarulzaman, K. (2013). Statistical optimization of enzymatic degradation process for Oil Palm Empty Fruit Bunch (OPEFB) in rotary drum bioreactor using crude cellulase produced from Aspergillus niger EFB1. Biochem. Eng. J., 75: 8-20. [ Links ]
Penín, E., Albernas, Y., González, E., Cervantes, Y. & Feyt, R. (2010). Análisis del proceso de obtención de alcohol extrafino en una destilería. Centro Azúcar, 37(1), 8-14. [ Links ]
Pernalete, Z., Piña, F., Suárez, M., Ferrer, A. & Aiello, C. (2008). Fraccionamiento del bagazo de caña de azúcar mediante tratamiento amoniacal: Efecto de la humedad del bagazo y la carga de amoníaco. Bioagro, 20(1), 3-10. [ Links ]
Peters, M. S. & Timmerhaus, K. D. (1968). Plant design and economics for chemical engineers. Edición Revolucionaria, Segunda Edición. La Habana: Instituto del Libro. [ Links ]
Pinto, J. M., Montagna, J. M., Vecchietti, A. R., Iribarren, O.A. & Asenjo, J. A. (2001). Process performance models in the optimization of multiproduct protein production plants. Biotechnol. Bioeng., 74(6), 451-465. [ Links ]
Ramírez, C. A. (2001). Energetics of Brazilian ethanol: Comparison between assessment approaches. Energy Policy, 39(8), 4605-4613. [ Links ]
Ravemark, D. E. & Rippin, D. W. T. (1998). Optimal design of multi-product batch plant. Comput. Chem. Eng., 22(12), 177-183. [ Links ]
Reales-Alfaro, J. G., Trujillo, L. T., Arzuaga, G., Castaño, H. & Polo, A. (2013). Acid hydrolysis of water hyacinth to obtain fermentable sugars. CT&F - Ciencia, Tecnología y Futuro, 5(2), 101-112. [ Links ]
Salomone, H. E. & Iribarren, O. A. (1992). Posynomial modeling of batch plants: A procedure to include process decision variables. Comput. Chem. Eng., 16(3), 173-184. [ Links ]
Salomone, H. E., Montagna, J. M. & Iribarren, O. A. (1994). Dynamic simulations in the design of batch processes. Comput. Chem. Eng., 18(3), 191-204. [ Links ]
Sammak, B., Rousta, K., Tabari, Z. & Yazdanian, S. (2007). Preliminary cost analysis on bioethanol plant. A report on the course bioethanol design. 6th National Energy Congress, Tehran, Iran. [ Links ]
Seider, W. D., Seader, J. D. & Lewin, D. R. (2003). Product and process design principles. Synthesis, analysis, and evaluation. Second Edition. Pennsylvania: John Wiley and Sons, Inc. [ Links ]
Trinder, S. (2014). ICIS pricing Ethanol, Ed. Reed Elsevier plc group. [Online]. [Consulted: April 2014]. Available at: <http://www.icis.com/energy/ethanol/latin-america/> [ Links ]
Yeh, N. C. & Reklaitis, G. V. (1987). Synthesis and sizing of batch/semicontinuous processes: single product plants. Comput. Chem. Eng., 11(6), 639-654. [ Links ]
AUTHORS
Yailet Albernas-Carvajal
Affiliation: Universidad Central “Marta Abreu” de Las Villas
Degree in Chemical Engineering, Universidad Central “Marta Abreu” de Las Villas
M. Sc. in Process Analysis in Chemical Industry, Universidad Central “Marta Abreu” de Las Villas
Ph. D. in Technical Science (Chemical Engineering), Universidad Central “Marta Abreu” de Las Villas
e-mail: yailetac@uclv.edu.cu
Gabriela Corsano
Affiliation: Instituto de Desarrollo y Diseño (INGAR), CONICET
Degree in Applied Mathematics, Universidad Nacional del Litoral
Ph.D. in Engineering, Universidad Nacional del Litoral
e-mail: gcorsano@santafe-conicet.gov.ar
Marlén Morales-Zamora
Affiliation: Universidad Central “Marta Abreu” de Las Villas
Degree in Chemical Engineering, Universidad Central “Marta Abreu” de Las Villas
M.Sc. in Process Analysis in Chemical Industry, Universidad Central “Marta Abreu” de Las Villas
Ph.D. in Technical Science (Chemical Engineering), Universidad Central “Marta Abreu” de Las Villas
e-mail: marlenm@uclv.edu.cu
Meilyn González-Cortés
Affiliation: Universidad Central “Marta Abreu” de Las Villas
Degree in Chemical Engineering, Universidad Central “Marta Abreu” de Las Villas
M.Sc. in Process Analysis in Chemical Industry, Universidad Central “Marta Abreu” de Las Villas
Ph. D. in Technical Science (Chemical Engineering), Universidad Central “Marta Abreu” de Las Villas
e-mail: mgonzalez@uclv.edu.cu
Ronaldo Santos-Herrero
Affiliation: Universidad Central “Marta Abreu” de Las Villas
Degree in Chemical Engineering, Universidad Central “Marta Abreu” de Las Villas
Ph.D. in Technical Science (Chemical Engineering), Universidad Central “Marta Abreu” de Las Villas
e-mail: ronaldo@uclv.edu.cu
Erenio González-Suárez
Affiliation: Universidad Central “Marta Abreu” de Las Villas
Degree in Chemical Engineering, Universidad Central “Marta Abreu” de Las Villas
Ph.D. in Technical Science (Chemical Engineering), Universidad Central “Marta Abreu” de Las Villas
Dr. Sc., Universidad Central “Marta Abreu” de Las Villas
e-mail: erenio@uclv.edu.cu

















































 kl0
kl0