1. INTRODUCTION
An efficient mechanism to increase oil production in heavy oil fields is the implementation of the In Situ Combustion (ISC) process. During the process, part of the crude oil present in the reservoir is oxidized, generating heat, which increases the mobility of oil due to the reduction of its viscosity, Sarathi [1]. The increase in oil production is associated with mechanisms of displacement by combustion gases, displacement by steam, reduction of viscosity due to the action of temperature, and thermal expansion of crude oil, among others.
Not all reservoirs are suitable to carry out ISC processes. Therefore, prior to its implementation at the field, feasibility studies at experimental level and numerical simulation of reservoirs are conducted. Experimental studies are performed in order to understand the oxidation characteristics of a given fluid/matrix System; in particular, experimental studies can be classified in two types: quantitative and qualitative. Among the quantitative studies, combustion tube is to be highlighted, which, among other things, allows for determining process performance parameters such as the amount of oil burned and the speed of advance of the combustion front. On the other hand, among the qualitative analysis, the following stand out: RTO (ramped temperature oxidation), TGA (thermogravimetric analysis), DSC (differential scanning calorimetry), DTA (differential thermal analyzer) and ARC (accelerating rate calorimetry); these types of experiments are cataloged as screening tools that allow to determine if a matrix/ fluid system meets the characteristics of a good candidate to ISC, Huang and Sheng [2]. These experiments are also used for the formulation of kinetic models that are subsequently validated by numerical simulation models; kinetic models consist of a reaction scheme and a kinetic triplet (activation energy, reaction frequency or pre-exponential factor and a reaction model).
The interpretation of qualitative experiments aimed at the formulation of kinetic models can be classified basically in two groups; the first one is based on the pre-establishment of a reaction model and the subsequent derivation of the kinetic parameters (activation energy and pre-exponential factor) from the Arrhenius equation, conventional method. The second, isoconversional method, Cinar [3], allows to identify if the oil under study has favorable characteristics to support an air injection process, does not require prior assumption of a reaction model, and allows for direct determination of the effective activation energy.
Isoconversional analysis is a technique that has been widely applied in kinetic studies of varied chemical processes; however, the adaptation of this technique to the study of kinetics in reactions associated with the ISC process was carried out by Cinar et. al [4]. From its first application for the study of kinetics in the reactions involved in the ISC process, there has been no clarity on how the value of the pre-exponential factor could be estimated, considering that it is not a direct measure of the mathematical models used for the analysis of experimental data.
Vyazovkin [5] presented a compendium of some correlations proposed in the literature for the application of the reaction model associated with isoconversional methods. In this paper, a mathematical procedure is proposed that allows for estimating the pre-exponential factor using the correlations presented by Vyazovkin [5]. Furthermore, the oxidation characteristics of a fluid/ matrix system corresponding to a Colombian heavy oil field are evaluated. To carry out this research, the experimental results reported by Padilla [6] were used, where the RTO reactor of the air injection laboratory of the Colombian Petroleum Institute (ICP) was used to study the oxidation characteristics of a fluid/matrix system belonging to a Colombian heavy oil field.
2. THEORETICAL FRAMEWORK
The oil oxidation process is usually expressed based on elementary reactions involving pseudo-components, which are grouped based on the fact that the behavior of crude oil phases is controlled by PVT (Pressure, Volume and Temperature) data. In general, it is established that at least two reactions must occur: one in which the fuel is deposited and another in which it is consumed, Chen [7]. Although assuming elementary reactions is an accepted practice for modeling the ISC process, it must be emphasized that the oxidation of crude during the ISC involves hundreds or thousands of reactions in tandem and in parallel, with a high degree of exothermicity.
The reaction rate can be expressed based on Equation 1.
Where k(T) represents the rate constant and f (C) the model of reactions. The rate constant depends on temperature and is usually expressed from the Arrhenius equation. On the other hand, the reaction model depends on the concentration of the reagents. As can be observed in Equation 1, the reaction rate is a function of both the temperature and the concentration of reagents. With the aim of simplifying calculations to study reaction kinetics, Friedman [8] proposed that for a same conversion value, the reaction rate is only a function of temperature. The foregoing implies that for different experiments carried out at different heating rates, the value of f (C) is independent of temperature, as it depends only on the concentration of reagents, which can be expressed as a function of conversion (X) and can be estimated from oxygen consumption. Therefore, Equation 1 can be expressed through Equation 2
For a reactor batch, the reaction rate according to Equation 2 would be:
The linear shape of the Equation 3 is:
Equation 4 is the base expression for the application of different isoconversional methods.
To apply the isoconversional analysis, a series of experiments must be performed varying the heating rate, on which basis t is possible to obtain the activation energy by of integral and differential isoconversional methods. The first one determines the activation energy from temperature data and the heating rate for the experiments conducted. On the other hand, the differential methods determine the activation energy starting from the reaction rate and the temperature profiles, using Equation 4. The latter are the most commonly used, due to their simplicity and reliability,
With respect to the Friedman's differential method, the left part of Equation 4 related to the inverse temperature, for each of the tests carried out, obtaining the activation energy from the slope of isoconversion values. The value of the intercept includes the reaction model and the pre-exponential factor. The latter are assumed as constant for the different conversion values and also constant for the various heating rates,
After applying the isoconversional principle on the experimental results of a set of RTO tests performed on a heavy crude oil, an activation energy versus conversion energy graph is obtained, similar to that presented in Figure 1. On this one, it would be possible to overlay an intercept graph vs conversion, In A * f(X), expecting a similar behavior to that observed in Figure 1. A behavior of this type indicates the consistency of the results [8].
Isoconversional methods do not provide direct information about the ore-exponential factor and the reaction model. However, Friedmar [8] presented a mathematical procedure for estimating the pre-exponential factor for elementary reactions, assuming that the reaction model approximates
Whereas the Equation 5 is a good approximation of the reactions model, by multiplying each side of the Equation 5 by A and taking the natural logarithm, you have:
Plotting the intercept of Equation 4 (lnA*f(X)) vs ln(l-X), a straight line is obtained which intercept represents the natural logarithm of the pre-exponential factor, according to Equation 6.
In addition to the approach of the reaction model suggested oy Friedman, some additional ones have been presented in the literature, Vyazovkin [5] presents a summary of some of them, or which the same procedure presented above could be applied (see Table 1). However, it must be taken into account that this procedure must be applied foreach group of reactions identified in the analysis of the crude oil fingerprint (graph of activation energy versus conversion), given that the above-described procedure described was proposed for elementary reactions.
3. EXPERIMENTAL DEVELOPMENT
To perform this work, a series of tests were programmed using the RTO reactor from Colombian Petroleum Institute (ICP). The equipment is fully automated and consists of a gas injection system (nitrogen or air), a tubular reactor where the rock/crude sample s kept, on which a linear increase in temperature is applied, plus a gas measuring system that allows quantifying the amount and concentration of effluent gases (CO, C02 and 02). Moreover, the equipment has security systems that ensure the integrity of people and instrumentation with respect to overpressure, high temperatures and high flows of injection gas. All process variables are monitored and stored in a computer. Figure 2 is an image of the equipment.
As described in the literature, for the application of isoconversional analysis, at least three RTO tests are required, Glatz [9], at three different heating rates, keeping other operational parameters constant. Based on this, three RTO trials were scheduled with the experimental conditions presented in Table 2.
The oil/rock ratio is part of the protocol established by the air injection laboratory of the Colombian Petroleum lnstitute: considering that the mass of oil loaded in the reactor must be sufficient so that the amount of carbon oxides generated can be measured by the gasometer, not generating deviations from the imposed heating ramp. For conducting the experiments, dead oil from a Colombian heavy oil field was used, which was dehydratec until reaching a water content of 0.8%. Figure 3 shows the behavior of oxygen consumption versus time and Figures 4 and 5 show the production of carbon oxides for each of the RTO tests carried out.
4. RESULTS ANALYSIS
Figure 3 shows three peaks of oxygen consumption for each one of the tests. The first two peaks represent the regions of oxidation at Low and high temperatures. In particular for the fluid/matrix system studied it is observed that the first peak of oxygen consumption is greater than the second, contrary to the expected behavior for heavy crude, Gutiérrez et al. [10]. However, this is not observed in the production curves of carbon oxides (Figures 4 and 5), where the first peak is less than the second. Considering that oxygen moles consumed in the production of carbon oxides can be approximated with Equation 7, the oxygen consumed by the addition reactions was determined (Figure 6), finding that the amplitude of the first peak is the product of the occurrence of this type of reactions, evidence of the high reactivity of the fluid analyzed. It also suggests the possibility of achieving spontaneous ignition during process field implementation, Padilla [6] and Padilla et al. [11].
Regarding the third peak, a previous investigation carried out on the fluid/matrix system studied, Trujillo [12] determined that this is the product of the reaction between oxygen and some component of the rock matrix at temperatures close to 550° C, discarding that the peak was caused by a reaction with organic matter in the matrix, as there was no third peak in the production curve of carbon oxides (CO2 and CO). Figure 4 shows the production of CO2 for each of the tests, thus ratifying what was stated by Trujillo [12].
CALCULATION OF THE PRE-EXPONENTIAL FACTOR
The Friedman differential method was used to obtain the activation energy graph as a function of the conversion (Crude fingerprint). Figure 7 shows the estimated activation energy for the set of RTO tests performed, as well as the intercept as a function of oxygen conversion. It is to be noted that both the Fingerprint and the intercept follow the same trend, which indicates, as mentioned by Friedman [8], the consistency in the kinetics of the reactions associated with the process.
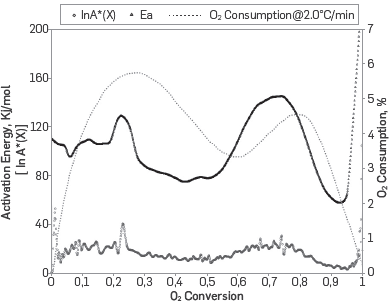
Figure 7 Crude fingerprint, Intercept of the Friedman method and Consumption of oxygen against conversion.
Cinar [3] recommended overlaying the oxygen consumption curve on the fingerprint, to identify groups of dominant reactions and associate them with each of the three-oxidation regions established for ISC studies. The regions or regimes of oxidation are: oxidation at low temperatures (LTO - Low Temperature Oxidation), oxidation at intermediate temperatures (MTO - Middle Temperature Oxidation) and oxidation at high temperatures (HTO - High Temperature Oxidation). Figure 8 shows the activation energy vs the average temperature in the three RTO tests, this graph allows to associate a range of temperatures to each oxidation region and / or group of reactions.
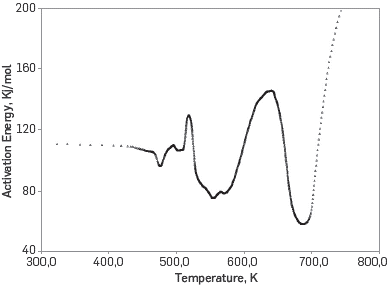
Figure 8 Fingerprint of the crude under study, Activation energy vs Average temperature in the three RTO tests.
Observing the crude fingerprint, it was found that the process is clearly dominated by three reactions, Padilla et al. [11]. The first one occurs in the LTO region between conversion values of 0.08 -0.27 and temperatures of 170 - 260 °C, with an activation energy of approximately 114 kJ / mol. The second reaction corresponds to an endothermic reaction associated with the MTO region and it occurs between conversion values of 0.4 - 0.5 and temperatures of 280 - 300 °C with an activation energy of approximately 80 kJ / mol. Finally a reaction was identified in the HTO regime with an activation energy of approximately 140 kJ / mol, and it occurs with conversion between 0.7 - 0.8 and temperatures of 350 - 400 °C. After determining the average activation energy for each of the reaction groups, we proceeded to implement the method proposed by Friedman and the power law correlations presented by Vyazovkin [5] to approximate the pre-exponential factor for each reaction Table 3 shows the results obtained after applying the proposed procedure, where it is observed that:
The pre-exponential factor calculated for the LTO and MTO regions is within the same order of magnitude range, regardless of the model used to approximate the reaction model (see Figures A1-A10).
In the HTO region, it can be observed that the model used has a significant effect on the pre-exponential factor, with variations of up to four orders of magnitude. The main reason for this behavior is that the graph lnA * f(X) vs lnf(X) of the Friedman reaction models and Power Law (P2/3) do not present the same degree of linearity as the others (see Figures All - A15) therefore, the slope and the intercept for these two graphs are different, resulting in significant differences in the estimated values for the pre-exponential factor.
Padilla et al.13], proposed a kinetic model, based on the experiments used in this work, achieving an acceptable reproduction of the oxidation behavior of the matrix fluid system in a reservoir numerical simulator. In their work they considered the pre-exponential factor as an adjustment parameter, obtaining values of 8.27E + 09, 5.00E + 07 and 3.72E +10 for the LTO, MTO and HTO regions, respectively In general, the pre-exponential factor values presented in Table 3 are close to those estimated by Padilla et al. [13], show that the procedure used for the approximation of the pre-exponential factor is a very useful tool for the formulation of kinetic models Intended to represent the oxidation behavior of heavy crude in commercial numerical simulators.
CONCLUSIONS
The isoconversional analysis technique has been widely used to study the oxidation characteristics of different fluid/matrix systems, candidates for ISC processes, allowing to eliminate the dependence on the reaction model over kinetic studies of reactions, identify groups of dominant reactions during the oxidation of oil, and estimate the effective activation energy for each of these reactions. Nevertheless, a procedure to estimate the pre-exponential factor has not been considered to date. In this regard, this paper shows that although the pre-exponential factor is not a direct measure of isoconversion methods, it is possible to obtain an approximation based on a simple mathematical treatment. This is a useful tool for building kinetic models Intended for the representation of the oxidation behavior of fluid systems/matrix, candidates for SC processes, using commercial numerical reservoir simulator software.














































