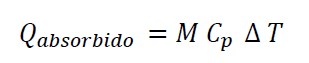Introducción

Considerada por sus propiedades como un producto lácteo, la leche de soya es empleada actualmente para elaborar un conjunto amplio de derivados que tienen una gran demanda en la población por su alta digestibilidad y valor nutritivo. Precisamente se reportan varias investigaciones dirigidas al perfeccionamiento de una de las etapas del proceso, entre ellas las realizados por Acuña Reyes et al. (²⁰¹¹), Chico et al. (²⁰¹⁷), Hernández et al. (²⁰¹⁵), Rodríguez et al. (^2017a) y Hernández Beltrán et al. (²⁰¹²).

Por su parte, diversos estudios evidencian la intención de generalizar el empleo de la soya como alimento humano, entre los que se encuentra el trabajo sobre los derivados de soya y la reducción de los antinutrientes de este producto presentado por Acuña Reyes et al. (²⁰¹¹), pero también se estudia el procesamiento del haba (^{Mateos-Aparicio et al., 2008}), la cinética de secado de semillas de soya (^{Vega León et al., 2017}), la calidad sensorial del néctar de mango enriquecido con soya (^{Montalvo-Perdomo et al., 2016}) y el empleo de maíz y soya en la elaboración de pan (^{Hernández et al., 2015}). En estos estudios destacan (entre los asociados a la producción de derivados): la elaboración de quesos mezclando leche de soya y de vaca (^{de Luna Jiménez, 2018}), el desarrollo de un queso crema con leche de soya y búfala (^{Rodríguez et al., 2017b}), la elaboración de leche fermentada a partir de arroz, leche de búfala y soya (Rodríguez et al., 2017a), las etapas de la producción de análogos al queso con pastas de soya (^{Barcenas Ochoa et al., 2017}), la elaboración de yogur a base de soya con quinua y camote (^{Chico, Romero, Hernández, & García, 2017})(^{Chico et al., 2017}) y la estabilidad del aderezo de soya (^{Vives et al., 2017}).

Como se aprecia, los trabajos recientes están dirigidos al mejoramiento del producto o de algunas de las etapas del proceso, pero los problemas actuales en la industria láctea requieren para su estudio de un enfoque multilateral que posibilite la intensificación global de la producción (^{García-Noa et al., 2015}). Por otra parte, es necesario realizar un análisis de la demanda y el consumo de portadores energéticos, en especial para las industrias procesadoras de alimentos, debido a que el uso eficiente de la energía incide tanto en la calidad del producto como en su costo de producción.

La leche de soya es el producto obtenido de la trituración en medio acuoso caliente del cotiledón del frijol de soya, al que se le inactivan las enzimas y se reducen los carbohidratos indeseables mediante un calentamiento severo, además de requerir condiciones especiales de enfriamiento (^{Resolución N.° 139/08}). Debido a sus requerimientos, el proceso es costoso y de ahí la importancia de establecer condiciones de operación que resulten eficientes en el uso de la materia prima y los portadores energéticos, quedando aún mucho potencial por aprovechar en la tecnología en estudio (^{García-Noa et al., 2015}).

Una vía para definir las mejores condiciones de operación mediante un estudio integral es el empleo de las técnicas del análisis de proceso, que es un método general de investigación científica. Este se ha empleado como el fundamento de una estrategia experimental para el aumento de la productividad de los procesos, basado en la modelación matemática y la simulación.

Los modelos matemáticos para la simulación pueden ser obtenidos al emplear los métodos de la matemática multivariada, la cual agrupa a un conjunto de técnicas que permiten al investigador interpretar y visualizar conjuntos grandes de datos (tanto en individuos como en variables), a partir de su simplificación o reducción. Entre las técnicas multivariadas más utilizadas para hallar la relación entre las variables se encuentran: el análisis de conglomerados, los componentes principales y los mínimos cuadrados parciales (^{Cerretani et al., 2011}; ^{Patras et al., 2011}; ^{Burbano & Moreno, 2018}). En estos métodos, las variables están correlacionadas entre sí y generalmente se supone que el conjunto de variables que intervienen en el análisis poseen una distribución normal multivariada. Esta suposición permite que el análisis multivariado se desarrolle paralelamente al correspondiente análisis univariado basado en una distribución normal (^{Lima de Aguiar et al., 2009}; ^{Ramírez et al., 2017}; ^{Barrera et al., 2020}).

Ante la necesidad de definir las condiciones de operación que incrementen la eficiencia del proceso, se realizó el estudio para dar respuesta a la siguiente interrogante: ¿es posible establecer modelos matemáticos que permitan conocer el efecto de los cambios en las variables del proceso sobre los indicadores productivos? A partir de la situación planteada, se definió como objetivo establecer la relación funcional entre el consumo de vapor por masa de leche producida y el de masa de leche producida por masa de materia prima utilizada, con los parámetros de operación mediante métodos multivariados en la producción de leche de soya. Dada la situación, en esta tecnología puede plantearse que el uso poco eficiente de las materias primas y de los portadores energéticos en algunas etapas de la producción de leche de soya provocan pérdidas y encarecen el producto, por lo que a medida en que en cada fase del proceso se trabaje óptimamente, se reducirán los costos y se hará más atractivo desde el punto de vista económico. Estas condiciones de operación pueden determinarse al emplear los modelos ajustados.

Materiales y métodos

El análisis del proceso de obtención de la leche de soya en la línea de producción se desarrolló con una selección previa de 20 variables, por ser las que están relacionadas con el uso de los materiales y de la energía en cada etapa del proceso, por lo que es de esperar que tengan una buena correlación con los índices de consumo que se calculen. Además, se recopilaron valores en 25 producciones en la misma instalación, de ellas 14 con 5600 l de leche producida y el resto fueron producciones de aproximadamente 15.000 l.

Independientemente del volumen de producción, la leche se debe obtener con la misma composición y calidad dada por la norma del proceso, diferenciándose solo en el uso que se le da a la leche. Las producciones de 15.000 l se emplearon posteriormente para producir yogur de soya y con las de 5600 l se produjeron otros derivados, como crema ácida, helados, entre otros, por lo que la relación entre las variables medidas y los índices de consumo fueron las mismas, independientemente del volumen de producción.

La variable medida o calculada con los datos primarios fue la pureza del cotiledón de soya empleado en el proceso (Ps), que es un dato obtenido del laboratorio de control de calidad de la fábrica; para conocer la masa de soya hidratada que entró al molino 1 (m_sM1) se midió directamente la masa de soya que entra al proceso y se le sumó el agua que se alimentó al molino I (FaM₁). Este flujo y el del agua que entró a la canal con tornillo sinfín (Fae) fueron medidos con los flujómetros instalados en línea que poseen una precisión de ± 1 l/min.

Por su parte, las masas de los otros componentes en el proceso se calcularon a partir de la medición del flujo del fluido, medido con un flujómetro en línea (que poseen una precisión de ± 1 l/min), multiplicado por el tiempo de operación. Las variables obtenidas por esta vía fueron: masa del agua que entra al calentador de agua (m_aCA), masa del agua que se suministra al molino 1 (m_aM1), masa del agua que va a la canal con tornillo sinfín (m_aTSF), masa de leche de soya que va al calentador de leche (m_lCL) y masa de leche de soya que va al intercambiador de tubo en tubo (m_lTT).

Las masas de vapor empleadas en las etapas de calentamiento a lo largo del proceso se calcularon dividiendo la energía transferida por el vapor entre la variación de entalpía del vapor a la presión correspondiente. Estos cálculos se emplearon para conocer las siguientes variables: masa de vapor que entra al calentador de agua (m_vCA), masa de vapor que se suministra al calentador de leche (m_vCL) y masa de vapor que se suministra a la canal con tornillo sinfín (m_vTSF). Así, la masa de vapor total consumida en el proceso (m_vT) resulta de la suma de las masas anteriores.

Ahora, la energía transferida utilizada en los cálculos anteriores se obtiene por la ecuación 1:

ecuación 1

Donde:

Q absorbido: calor absorbido por el componente (kJ)

M: masa del componente (kg)

Cp: capacidad calórica del componente (kJ/ kg °C)

ΔT: gradiente de temperatura del fluido que se calienta (°C)

Los valores de temperatura de las corrientes se obtuvieron directamente en cada equipo mediante termómetros bimetálicos instalados en línea, los cuales poseen una precisión de ± 1 °C y donde las variables obtenidas por esta vía fueron: temperatura del agua que entra al calentador de agua (T_aCA), temperatura del agua que entra al molino 1 (T_aM1), temperatura de la leche de soya que entra al calentador de leche (T_lCL), temperatura de la leche de soya que entra al tanque flash (T_lTF), temperatura de la leche de soya que entra al tubo de retención (T_lTR), temperatura de la leche de soya que entra al intercambiador de tubo en tubo (T_lTT), temperatura de la solución de bicarbonato de sodio (T_Sb) y temperatura inicial de la soya (T_s).

Se consideró como tiempo de molida (t_m) el periodo transcurrido desde que comienza a caer el grano en el molino hasta que terminó esta operación, donde para la tabulación y la organización de todos estos datos se utilizó el programa Microsoft Excel y en el procesamiento se empleó el programa Statgraphics Centurion.

La modelación multivariada del proceso se realizó siguiendo un procedimiento general a través de cuatro pasos fundamentales, donde se tuvieron en cuenta experiencias anteriores en la aplicación de las técnicas del análisis de procesos (^{Zuluaga Dominguez, 2011}; ^{Hernández Beltrán et al., 2012}; ^{Barrera et al., 2020}):

En el análisis de los datos se describió el comportamiento de las variables, al calcular para cada una de ellas: el promedio, los valores máximos y mínimos y el coeficiente de variación, además se obtuvieron los coeficientes de correlación entre todas las variables analizadas.

Para la obtención de los conglomerados se utilizaron el método del vecino más cercano y la métrica de distancia euclidiana cuadrada y se tuvieron en cuenta experiencias anteriores en producciones lácteas (^{Avilez et al., 2010}; ^{García-Noa et al., 2015}; ^{Barrera et al., 2020}), además, se estandarizaron los datos para que todas las variables estuvieran dentro de un mismo intervalo de valores. El análisis se realizó para las observaciones (producciones) buscando diferencias y similitudes entre ellas.

Para identificar el número óptimo de conglomerados se empleó el método del gráfico de la distancia de aglomeración, que es la herramienta de la que dispone el Statgraphics Centurion para esto (^{Statgraphics, 2016}). Al aplicar este método, el número de conglomerados óptimo es el que produzca la mayor diferencia entre las distancias de los centroides de los grupos sucesivos, lo que se aprecia en el cambio brusco en esta distancia al recorrer los diferentes estados, así, un estado se corresponde con un nuevo grupo formado. Este método es similar al método del codo (Elbow Method), el cual se encuentra en otros softwares como el R, en el que la selección del número de conglomerados óptimo se basa en la inercia, definida esta como la suma de las distancias al cuadrado de cada objeto del conglomerado a su centroide, donde en este método se produce en el óptimo, un cambio brusco en el gráfico de inercia contra el número de grupos (^{Tibshirirani et al., 2001}). En el software Statgraphics, el procedimiento de componentes principales está diseñado para extraer los componentes principales de un conjunto de variables cuantitativas y para aplicarlo se estandarizaron los datos experimentales, de forma que todas las variables estuvieran dentro de un mismo intervalo de valores (^{Statgraphics, 2016}).

El objetivo fundamental de aplicar la técnica multivariada del análisis de componentes principales es la reducción de variables mediante la obtención de correlaciones lineales entre las variables, lo que conforma los componentes que explican la mayor variabilidad posible de los datos. Además, se emplea como paso previo al método de mínimos cuadrados parciales para definir el número de componentes a utilizar en los modelos matemáticos a ajustar. Se tiene en cuenta que la selección del número de factores adecuados se realizó mediante el gráfico de sedimentación, el cual muestra los porcentajes de varianza que explican cada uno de los componentes por separado. Así, en este gráfico se busca el número de componentes que explique un porcentaje acumulado superior al 85% de la varianza total de los puntos experimentales (^{Piovoso & Hoo, 2002}; ^{Statgraphics, 2016}).

En el análisis pormcp se ajustó la cantidad de componentes que se obtienen del procedimiento de componentes principales con 20 variables independientes, donde se declara variable dependiente de un modelo la razón que relaciona la masa de vapor total y la masa de leche obtenida (I₁) y del otro modelo la razón que establece la relación entre la masa de leche producida y la masa de soya inicial (I₂).

Para cada variable dependiente (I₁ e I₂) se obtuvieron dos modelos, uno con las variables experimentales estandarizadas centrando por la media, el cual se empleó para identificar las variables significativas estadísticamente y conocer la influencia de cada una de ellas sobre dicho índice. El otro modelo para cada índice se obtuvo con las variables no estandarizadas y se empleó para realizar la simulación con las unidades de medidas originales de cada variable independiente. En total se ajustaron cuatro modelos por mcp y la significación de los modelos se analizó con un 95% de confiabilidad a través del valor-p de la razón de Fisher. La calidad de predicción se analizó a través del valor Press (sumatoria cuadrada del error de predicción) (^{Piovoso & Hoo, 2002}; ^{Statgraphics, 2016}).

Los modelos se validaron por el método “sacar uno a la vez”, en el cual se ajusta el modelo y se deja una producción sin incluir que después se utiliza para calcular el error de predicción. Este procedimiento se repite tantas veces como cantidad de producciones hay y, finalmente, se reporta el promedio de los errores obtenidos en dichos cálculos. El modelo obtenido por el método de mcp con las variables no estandarizadas se empleó para evaluar alternativas de mejora en las condiciones de operación mediante la simulación, donde se busca que se incremente el rendimiento en la etapa y se tiene en cuenta que los valores de las variables de operación que más favorezcan este propósito estén dentro de los valores alcanzados en las producciones estudiadas. Para ello, se consideró el signo de los coeficientes de las variables y los valores experimentales, donde los coeficientes con signo positivo indican que se deben utilizar a los mayores valores de las variables y los de signos negativos a los menores valores de las variables para obtener el mayor rendimiento (^{Barrera et al., 2020}).

Resultados y discusión

El análisis de los datos comenzó al determinar el coeficiente de correlación entre todas las variables medidas durante el proceso productivo, identificándose aquellas con correlaciones estadísticamente significativas, estas se muestran en el correlograma de la figura 1, donde también se aprecia que la mayoría de los coeficientes obtenidos se encontraron entre 0,60 y 0,90, lo que manifiesta un vínculo estrecho entre los valores de estas variables.

El hecho de haber obtenido correlaciones significativas entre un gran número de variables medidas justifica el procesamiento de estas por el método de los mínimos cuadrados parciales.

Todas estas variables fueron incluidas en los análisis posteriores al considerar, además, que coinciden con variables empleadas en otros trabajos de evaluación del proceso de este producto (^{Rodríguez et al., 2017a}) y estudios realizados con productos similares (^{Avilez et al., 2010}; ^{García-Noa et al., 2015}).

El análisis de conglomerados se realizó para todas las observaciones con el método de vecino más cercano y la métrica de distancia euclidiana cuadrada. En la figura 2 se muestra el gráfico de la distancia de aglomeración que se empleó para identificar el número óptimo de conglomerados a obtener y en ella se aprecia que el cambio brusco en la distancia entre los centroides de los grupos se obtiene al arribar al estado 23, el cual se corresponde con dos conglomerados, por lo que se considera que el número óptimo de conglomerados es dos.

Fuente: Elaboración propia

Figura 1. Correlograma de las variables medidas durante el proceso con correlación estadísticamente significativa para un 95 % de confiabilidad. 

Que el número óptimo de conglomerados sea dos es compatible con las características de la base de datos experimental. En el dendrograma obtenido (figura 3) se observan los dos grandes grupos: uno formado por las primeras 14 corridas, que se corresponden con las producciones de 5600 l y otro grupo formado por las últimas 11, es decir, desde la corrida 15 a la 25, que son las producciones de 15.000 l.

Del primer grupo, cinco producciones (8, 9, 10, 1 1 y 14) se asemejan entre sí, que es un reflejo de que se empleó soya procedente de un suministrador diferente al que la proveyó en el resto de las producciones, lo que está reportado en los registros del laboratorio de control de calidad. En el otro grupo se refleja también este comportamiento, aunque menos marcado. Dentro del primer grupo es de notar que las producciones 12 y 13 son las de mayor distancia, lo que coincide con que son en las que hubo un mayor volumen de producción en las mismas condiciones de operación antes mencionadas. Del segundo grupo, la producción 24 es la menos semejante al resto de las producciones, lo cual se debe a que el volumen procesado es menor al resto.

Fuente: Elaboración propia

Figura 2. Gráfico de la distancia de aglomeración 

Fuente: Elaboración propia

Figura 3. Dendrograma de las observaciones del método del vecino más cercano con métrica distancia euclidiana cuadrada.Nota aclaratoria: las producciones de la 1 a la 14 corresponden a producciones de 5600 l y de la 15 a la 25 a 15.000 l. 

Es importante destacar la utilidad de este método multivariado para identificar semejanzas y diferencias en una misma línea productiva, lo cual se puede apreciar en el dendrograma obtenido en el análisis del proceso (^{Ruiz-Tamayo et al., 2021}; ^{Zuluaga Dominguez, 2011}). Una herramienta multivariada muy útil para decidir el número de componentes a utilizar en los modelos de componentes principales es el gráfico de sedimentación, el cual se muestra en la figura 4, donde se aprecia que basado en los vectores propios (eigenvalues), cuando se emplean cuatro o cinco componentes principales, los vectores propios están muy cerca de la unidad.

Fuente: Elaboración propia

Figura 4. Gráfico de sedimentación basado en los vectores propios 

En el análisis de componentes principales (tabla 1) se aprecia que con cuatro componentes se explica el 85,20% de la varianza total de los puntos experimentales y con cinco componentes se explica el 89,23% de la varianza total. Ambos valores son aceptables, ya que se garantizan con valores propios superiores a uno, que es lo requerido por el método. Se puede observar que un quinto componente incrementaría en solo un 4 % el acumulado de la varianza explicada, por lo que se justifica el uso de cuatro componentes en el ajuste por mínimos cuadrados parciales.

Tabla 1. Resultados del análisis de componentes principales 

Fuente: Elaboración propia

Con vistas a obtener la relación funcional entre las variables del proceso y los índices relacionados con la masa de vapor total y la masa de leche obtenida (I₁) y la relación entre la masa de leche producida y la masa de soya inicial (I₂), y al tener en cuenta los resultados obtenidos en el análisis de componentes principales, se aplicó el método de mínimos cuadrados parciales con cuatro componentes.

Los modelos obtenidos para los índices I₁ e I₂ con los coeficientes estandarizados se muestran en las ecuaciones 2 y 3, respectivamente:

ecuación 2

ecuación 3

En el análisis de varianza y de calidad de ajuste del modelo para I₁ (tabla 2 y 3) se observa que el modelo de la razón, entre la masa de vapor total y la masa de leche obtenida (I₁), presentó buena calidad de ajuste para un 95% de confiabilidad, con un valor-p inferior a 0,05. Además, el Press fue un valor del orden de 2,00 × 10^-4 que indica un error de predicción pequeño. Estos resultados reflejan lo adecuado del modelo obtenido, el cual puede ser útil para la evaluación energética del proceso, sustituyendo los valores de los parámetros de operación que relaciona, como ha sido empleado en otras investigaciones (^{Valencia García et al., 2007}; ^{Sariego Toledo et al., 2017}).

Tabla 2. Análisis de varianza y calidad de predicción del ajuste de mínimos cuadrados parciales para la razón masa de vapor total y la masa de leche obtenida (I₁) 

Fuente: Elaboración propia

Tabla 3. Calidad de predicción del ajuste de mínimos cuadrados parciales para la razón masa de vapor total y la masa de leche obtenida (I1) 

Fuente: Elaboración propia

Para el modelo de la relación entre la masa de leche producida y la masa de soya inicial (I₂), también se obtiene una buena calidad de ajuste para un 95% de confiabilidad, pues el p-valor para la razón de F es inferior a 0,05 (tablas 4 y 5) y posee un Press igual a 4,18 × 10^-2.

Mediante el análisis de los coeficientes estandarizados fue posible identificar la influencia de cada una de las variables independientes sobre los índices calculados y se observa que las seis variables que inciden en mayor proporción en la razón I. son: la masa de vapor que entra en el calentador de agua (m_vCA), el flujo de agua de enjuague que se desecha de la canal con tornillo sinfín (F_ae), la temperatura del agua que entra al calentador de agua (T_aCA), la masa de leche que va al intercambiador de tubo en tubo (m_lTT), la temperatura del agua que va al intercambiador de tubo en tubo (T_aTT), así como la temperatura de la leche que entra al calentador de leche (T_lCL).

Tabla 4. Análisis de varianza en el ajuste de mínimos cuadrados parciales para la razón la masa de leche producida y la masa de soya inicial (I₂) 

Fuente: Elaboración propia

Tabla 5. Calidad de predicción del ajuste de mínimos cuadrados parciales para la razón la masa de leche producida y la masa de soya inicial (I₂) 

Fuente: Elaboración propia

Sobre la razón I₂, las variables que inciden en mayor proporción son: la temperatura del agua que entra al calentador de agua (T_aCA), la masa de leche que va al intercambiador de tubo en tubo (m_lTT), la masa del vapor que entra al calentador de agua (m_vCA), el flujo de agua que entra al molino 1 (F_aM1), la temperatura de la leche que va al calentador de leche (T_lCL), así como la masa de leche que entra al calentador de leche (m_lCL), es decir, son variables que modifican significativamente los índices obtenidos, por lo que se debe tener un control riguroso sobre ellas.

Es de destacar que hay cuatro variables que coinciden en ambos modelos y que por lo tanto son aquellas sobre las cuales hay que tener un mayor control durante el proceso de producción. Este resultado indica la conveniencia de que en cada producción se garantice que la masa del vapor consumida en el calentador de agua, la temperatura de alimentación a este equipo, la temperatura del fluido que alimenta al calentador de leche y la masa de leche que entra al intercambiador cumplan con las especificaciones del control del proceso, pues inciden significativamente en la eficiencia productiva.

El modelo obtenido con las variables no estandarizadas se empleó para evaluar alternativas en las condiciones de operación, al buscar que mejoren los indicadores que caracterizan la eficiencia del proceso y tener en cuenta los valores de las variables de operación que más favorezcan este propósito.

Los modelos obtenidos para los índices I1 e I2 con los coeficientes no estandarizados se muestran en las ecuaciones 4 y 5, respectivamente:

ecuación 4

ecuación 5

Se comprobó la posibilidad de aplicar estas condiciones en la práctica al analizar que las variables pueden asumir esos valores sin ninguna contradicción desde el punto de vista técnico.

En la tabla 6 se presentan los valores utilizados para las distintas variables en la simulación, seleccionados entre los valores reales que tomó cada variable. Para coeficientes con signos positivos se escogió el mayor valor de la variable y para coeficiente con signo negativo el menor valor real de la variable.

Como resultado de realizar la simulación del proceso se obtuvo que se puede alcanzar un índice de 9,5 kg de leche producida por cada kg de soya procesada. Este valor, al ser estimado con el modelo ajustado de mínimos cuadrados parciales, posee un error de 4,18 × 10^-2 y es superior a 8,3 kg de leche producida por cada kg de soya procesada, que es el mayor valor obtenido en las producciones analizadas. Con este resultado se establece que existe un conjunto de condiciones de operación que puede garantizar el incremento de la eficiencia del proceso productivo.

Tabla 6. Condiciones de operación utilizadas para la simulación de I₂ 

Fuente: Elaboración propia

El efecto del cambio en las condiciones de operación calculado por la diferencia entre el mayor índice real (I₂) y el que se obtiene al trabajar bajo las condiciones recomendadas en la tabla 6 resultó ser positivo para un incremento de la producción de leche de soya anual en 1050 t, lo cual debe repercutir favorablemente en el balance económico de la fábrica por concepto de más leche de soya producida por kg de grano de materia prima procesada. Un efecto similar se ha reportado en la producción de queso crema (^{Valencia García et al., 2007}).

Dadas las semejanzas del proceso de producción de la leche de soya con otros productos lácteos y en general con otros muchos productos alimentarios y, al tener en cuenta la necesidad de realizar los estudios con un enfoque multilateral (^{García et al., 2015}, ^{Juárez-Barrientos et al., 2016}; ^{Pérez-Sánchez et al., 2020}), puede considerarse que el procedimiento a través de los cuatro pasos fundamentales utilizados en esta investigación tiene un grado de generalidad, lo que lo hace atractivo para servir de base metodológica en el empleo de las técnicas del análisis de proceso para el aumento de la productividad de las tecnologías. Así, será necesario, ante todo, un estudio detallado de la tecnología a analizar y definir las etapas y las variables de operación que intervienen en el proceso para luego realizar las mediciones y procesarlas para la obtención de los modelos que permitan evaluar condiciones de operación que mejoren la eficiencia.

Conclusiones

El análisis de conglomerados es una técnica multivariada que permitió clasificar las producciones más semejantes de la línea de producción de leche de soya y discriminar aquellas con diferentes volúmenes de producción, siendo dos el número óptimo de conglomerados para esta base de datos. El modelo multivariado obtenido con cuatro componentes principales mediante el método de mínimo cuadrado parciales para estimar la relación entre la masa de vapor total y la masa de leche de soya obtenida (I₁), en función de 20 variables de operación, presentó una buena calidad de ajuste para un 95% de confiabilidad, con un error de predicción pequeño del orden de 2,00 × 10^-4, el que es útil para la evaluación energética del proceso.

El modelo de regresión por mínimos cuadrados parciales, que establece la relación funcional entre la razón de la masa de leche producida, la masa de soya inicial (I2) y las 20 variables de operación, presenta una buena calidad de ajuste y posee un error cuadrático de predicción igual a 4,18 × 10^-2, lo que indica la posibilidad de su empleo para simular este proceso. Bajo las condiciones de operación propuestas y evaluadas con el modelo multivariado ajustado, se estima que se pueden obtener 9,5 kg leche por cada kg de granos de soya empleada en la producción, lo que mejora el balance económico de este proceso.

Descargos de responsabilidad

Todos los autores hicieron contribuciones significativas en el trabajo, no existen conflictos de intereses y están de acuerdo en la publicación de estos resultados.

Contribución de los autores

Edilia Gutiérrez Cordero: registro de información en campo, construcción de las bases de datos, análisis de la información y elaboración del manuscrito; Yanet Sariego Toledo: análisis de la información y elaboración del manuscrito; Eduardo García Noa: diseño de las metodologías, registro de la información en campo, supervisión de las actividades, análisis de la información y elaboración del manuscrito.

Implicaciones éticas

El presente artículo cuenta con el aval que consta en el acuerdo 3 del acta con fecha 10/12/2019 del Comité del programa de Análisis y Control de Procesos de la Facultad de Ingeniería Química de la Universidad Tecnológica de La Habana. Se obtuvo el consentimiento de la planta objeto de estudio para usar la información suministrada en la documentación del proceso presentado en el artículo.