1. Introducción
Una buena estimación de los costos tiene relación directa con el rendimiento y la eficacia de una organización, ya que una sobreestimación puede dar lugar a una pérdida de la participación de mercado y por ende generar pérdidas en el negocio, mientras que una subestimación puede dar lugar a pérdidas financieras para la empresa. Debido a estas posibles consecuencias, la estimación y el control de costos ha sido un punto focal para el diseño de planes operativos y estratégicos y un aspecto clave para la generación de políticas de gestión y las decisiones empresariales 1.
La exactitud de las estimaciones depende del nivel de incertidumbre y del control de los riesgos. La modelación y medición de los riesgos es una tarea compleja. La razón radica en la dificultad que existe para entender ciertas realidades, por ejemplo, poder seguir y predecir el movimiento de los precios de los activos financieros, entender la probabilidad de incumplimiento de un cliente, esto por hablar de variables económicas, pero también puede estar influenciado por variables sociales sin contar las humanas, como la racionalidad limitada y el oportunismo que puede crear situaciones que no puedan ser modeladas fácilmente tales como: la deshonestidad, hacer trampa y ofrecer información incompleta o distorsionada de manera premeditada a fin de lograr ventajas favorables 2,3.
Existen sin duda modelos interpretativos que ayudan a comprender ciertos episodios, sin embargo, a veces no proporcionan la exactitud que se requiere desde la teoría económica, por lo que se debe acudir a otras herramientas como los métodos estadísticos para su solución o para un mejor entendimiento 4.
Analizar riesgos se convierte así en la identificación y estimación de las distribuciones de probabilidad que se supone siguen las funciones de valor, por ejemplo el comportamiento de los precios en el caso de los riesgos de mercado, la probabilidad de no pago en el caso de los riesgos de crédito, la probabilidad de no poder cumplir con las obligaciones al corto plazo en el caso de riesgos de liquidez o de otro tipo de riesgo 5,6.
Entre los métodos que se han utilizado para el análisis de los riesgos se encuentran: las matemáticas de intervalos, la simulación de Monte Carlo y la teoría de conjuntos difusos. La matemática de intervalos tiene como desventaja que no tiene en cuenta las probabilidades en la representación de la incertidumbre 7. También se puede utilizar teoría de la lógica difusa 8,9.
El cuerpo de conocimiento de la teoría incluye conjuntos difusos, lógica y números difusos. Los conjuntos difusos permiten el manejo de la incertidumbre no estadística asociado con la incertidumbre de la información proveniente principalmente de opiniones de expertos 10. Estos métodos han sido utilizados en el análisis de la incertidumbre en sistemas de costeo 11-13. Un enfoque bien conocido en este contexto es el método de Monte Carlo el cual utiliza la lógica de la probabilidad y el volumen, este método puede incluirse en la rama experimental de las matemáticas que basada en probabilidades estadísticas apoya experimentos con números aleatorios 14.
En los procesos de producción, el riesgo se relaciona con la variación en los factores necesarios para la elaboración de un bien o servicio, dicha variación puede generar efectos adversos para las finanzas de una organización, pues los costos pueden ser superiores a los ingresos lo que afectaría la rentabilidad de una organización. Por lo anterior, el riesgo debe ser identificado y medido para generar medidas de mitigación que permitan su eliminación, reducción o control 15.
En los que respecta a los costos y la variabilidad de los factores de producción, los gerentes utilizan la retroalimentación sobre las desviaciones de costos para iniciar las acciones correctivas, preventivas o de mejora. Las preguntas para responder son ¿es necesario iniciar una acción correctiva cuando la desviación es pequeña?, ¿Cuándo una desviación es considerada, pequeña o grande para iniciar una acción correctiva?, estas preguntas son respondidas en este artículo.
La metodología de investigación utilizada fue Design Search Research (DSR) la cual permite resolver problemas mediante la creación de métodos, metodologías o artefactos 16, en consecuencia, para determinar los límites en los cuales las variaciones del costo de un producto o servicio se consideran normales se utilizó como metodología de estimación del costo el costeo basado en actividades (Activity-Based Costing o ABC, por sus siglas en inglés), el ABC permite calcular los costos con mayor exactitud y sirve como una herramienta para mejorar el desempeño organizacional 17,18. El ABC permite identificar actividades y procesos que no agreguen valor, mejorar la eficiencia de los procesos lo que a su vez genera una disminución de costos dentro de la organización.
El modelo desarrollado en este artículo se construye utilizando una lógica matricial del ABC la cual permite identificar de manera fácil y precisa los costos de cada actividad y es flexible en cuanto a los posibles ajustes que pueden ser necesarios como resultado de cambios en los procesos de producción 19.
La simulación de Monte Carlo fue utilizada para la determinación de los límites de tolerancia. De hecho, los modelos probabilísticos de cálculo de costos son herramientas que pueden utilizarse para hacer que los sistemas de costeo sean más relevantes, contribuyendo a mejorar la toma de decisiones. El modelo propuesto aprovecha las potencialidades del ABC y permite incluir la incertidumbre inherente a la elaboración de un producto o prestación de un servicio.
El modelo propuesto permite incluir las correlaciones entre los factores de producción y permite determinar límites de tolerancia de costos para los productos lo cual tiene implicaciones prácticas, ya que dichos límites pueden ser utilizados por los tomadores de decisiones como referencia para saber cuándo deben desarrollar acciones de mejoramiento y cuando el proceso se encuentra controlado.
2. Medición de la incertidumbre y costeo
La simulación se utiliza para valorar ciertos instrumentos y derivar medidas de riesgo cuando: no estén disponibles modelos analíticos, un modelo analítico no sea aplicable, o, el análisis costo beneficio favorezca el uso de la simulación.
En el ámbito de los costos, existen importantes fuentes de incertidumbre que influyen en su estimación. Uno de los primeros enfoques que se han utilizado para medir y entender la incertidumbre de los costos y medir el nivel de riesgo es el análisis de sensibilidad, dicho análisis ofrece una primera mirada a los tomadores de decisiones en el escenario sobre lo que sucedería si los insumos más relevantes cambiaran, considerando una situación optimista y una pesimista.
El enfoque de análisis de sensibilidad tiene algunas desventajas relacionadas con las variables, ya que no permite: su interacción al mismo tiempo, incluir las correlaciones entre ellas y tener en cuenta sus distribuciones de probabilidad.
Para mitigar estas limitaciones, se han diseñado herramientas basadas en métodos probabilísticos. Para estas herramientas la incertidumbre en los datos de costos se representa utilizando distribuciones de probabilidad. Los métodos probabilísticos son más robustos que el análisis de sensibilidad; sin embargo, como desventaja requieren una mayor cantidad de datos para su fiabilidad 20,21.
Teniendo en cuenta que una de las limitaciones del sistema de costeo ABC es no reconocer la incertidumbre 22, diversos autores han presentado modelos que han tratado de mitigar dicha limitación. Algunos autores se han centrado en la aplicación de conjuntos difusos 9,23,24. Estos autores presentan modelos de costos basado en actividades utilizando la lógica difusa para capturar la incertidumbre en las variables de entrada del modelo basado en actividades.
Nachtmann et. al. 8 estudiaron y compararon diferentes métodos para manejar la incertidumbre en sistemas ABC y concluyeron que la simulación de Monte Carlo y la teoría de conjuntos difusos son mejores que las matemáticas de intervalos para manejar la incertidumbre en tales sistemas de cálculo de costos. Dicho modelo utiliza estimaciones para calcular los costos de producto y servicios y los recursos necesarios para la elaboración de estos.
Esto se debe principalmente a que la recopilación de la información necesaria para generar el costo del producto es un proceso oneroso y una tarea que requiere mucho tiempo, dado que los datos de los sistemas de costeo se basan en datos históricos y a menudo se estiman, los valores reales de estos datos son inciertos y es probable que los datos de entrada sean imprecisos , sin embargo con técnicas como el aprendizaje automático o (machine learning, como es conocido normalmente) este problema puede ser superado 25. La necesidad de tener en cuenta la incertidumbre en las decisiones de planificación se remonta a los modelos de planificación funcional, en los que los recursos para el futuro se han asignado sobre la base de los datos actuales y las proyecciones futuras.
Algunos autores presentan el método de costeo junto con metodologías difusas o simulación de Montecarlo 26-28, con el fin de incluir la incertidumbre propia de los sistemas de producción que están analizando.
3. Metodología
La metodología de investigación utilizada fue Design Search Research (DSR) 16. La DSR tiene como objetivo resolver problemas reconocidos en las organizaciones a través de la creación y evaluación de artefactos 29 que son agrupados en cuatro tipos: constructos, modelos, métodos e instancias 29,30.
Teniendo en cuenta lo anterior, se desarrolló un modelo ABC matricial junto con Simulación de Monte Carlo para la toma de decisiones organizacionales en ambientes de incertidumbre. A continuación, se presenta la propuesta metodológica, una aplicación práctica con sus respectivos análisis y las conclusiones del artículo.
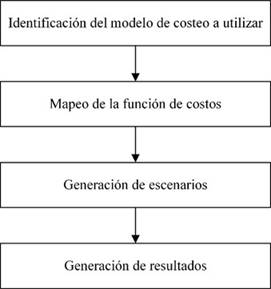
La propuesta para la determinación de los límites de tolerancia consta de 4 etapas que se pueden observar en la Figura 1.
Etapa 1. Identificación del modelo de costeo a utilizar
Se puede utilizar cualquier sistema de costeo, por procesos, por órdenes de producción, basado en actividades o basado en el tiempo. En este artículo se propone un modelo ABC matricial, adaptado de Afonso et al. 19, tal como se presenta a continuación:
Considere que: n recursos, m actividades y o productos y dados los siguientes parámetros:
cr j = Costo del recurso i
ar ij = Relación a través de un inductor de recurso i con la actividad j
arn ij = Variable 𝑎𝑟𝑖𝑗 normalizada
ca ij = Costo de la actividad j para cada recurso i
pa jk = Relación a través de un inductor de actividad j para el producto k
pan jk = Variable 𝑝𝑎𝑗𝑘 normalizada
cp k= Costo del producto k
CR= Matriz de costo de recursos
AR= Matriz relación actividad recurso
ARN= Matriz actividad recurso normalizada
CA= Matriz de costo de actividad
PA= Matriz relación actividad producto
PAN= Matriz relación actividad producto normalizada
CP=Matriz de costo de productos o servicios
Teniendo en cuenta estos parámetros, para la estimación del costo utilizando el modelo matricial tiene que:
La Ec. (1) representa el costo de los recursos utilizados:
La Ec. (2) presenta la relación existente entre las actividades y los recursos utilizados.
La Ec. (3) representa la relación entre actividades y recurso normalizado, teniendo en cuenta que se pueden considerar actividades donde no se esté agregando valor al producto o servicio, pero si se esté consumiendo recurso.
La Ec. (4), representa el costo de cada actividad.
En la Ec. (5), se relaciona las actividades con cada uno de los productos.
La Ec. (6) muestra la matriz actividad producto normalizada,
La Ec. (7), muestra el costo de cada uno de los objetos de costo, que pueden ser productos o servicios desarrollados por una organización.
Etapa 2. Mapeo de la función de costos
Una vez construido el modelo para la estimación del costo se procede al análisis de la variabilidad, para esto se asume que 𝑎𝑟ij, 𝑝𝑎jk, son parámetros que poseen incertidumbre dentro del proceso de producción, esto significa identificar aquellos factores (recursos, actividades o productos) que no son determinísticos y tienen incidencia significativa en el resultado final. Debe tenerse en cuenta el nivel y el impacto de la exposición a la variabilidad de los factores identificados.
Etapa 3. Generación de escenarios
En esta etapa se utilizan diferentes pruebas estadísticas y modelos de simulación tales como Simulación de Monte Carlo o pruebas retrospectivas. Una muestra de 𝑎𝑟𝑒 𝑖𝑗, 𝑝𝑎𝑒 𝑗𝑘 es generada para cada parámetro de entrada, 𝑎𝑟𝑖𝑗, 𝑝𝑎𝑗𝑘 usando su distribución empírica de probabilidad, la cual puede ser obtenida utilizando pruebas de ajuste de (por ejemplo, la prueba Anderson-Darling o la de Kolmogórov-Smirnov). Al repetir este procedimiento miles de veces, se obtiene un conjunto de resultados que representan la distribución de probabilidad del costo o servicio tal como se muestra en la Ec (8).
Un aspecto importante es que este modelo considera las posibles correlaciones que puedan existir entre los diferentes parámetros del modelo.
Etapa 4. Generación de resultados
Finalmente, los resultados son analizados utilizando herramientas estadísticas como los histogramas, intervalos de confianza, entre otros. Con la distribución de probabilidad obtenida en la etapa 3 se definen los límites asociados al número de desviaciones de la media para los cuales el costo obtenido del producto o servicio se considera normal y cuando el costo se considera fuera de control por lo que se deben generar medidas de intervención o de inspección más detalladas. El valor esperado del costo se podría considerar el “estándar”, y los límites establecidos alrededor de la tolerancia de las desviaciones con respecto a dicho “estándar”.
4. Resultados
La aplicación es para una empresa del sector transporte de carga, la cual tiene dos grandes actividades principales, la primera tiene que ver con las labores administrativas relacionadas con el servicio, y la segunda con la prestación de éste (carga, transporte y descarga).
La empresa cuenta con dos recursos principales los cuales son los camiones y los conductores. La empresa tiene establecidas 5 líneas de servicio de acuerdo con los kilómetros recorridos (100 km, 300km, 500km, 800km, y 900 Km), para cada una de estas rutas desea determinar el costo, teniendo en cuenta factores como el combustible en un mes, el mantenimiento de los camiones, los salarios de los conductores, los seguros, la parte administrativa, las depreciaciones, el dinero para los peajes, el espacio para oficina y para parqueo de los camiones. Se utilizó la metodología de costeo basado en actividades para la estimación del costo producción de cada una de las rutas (Ruta 1, Ruta 2, Ruta 3, Ruta 4 y Ruta 5) producidos en un período determinado. Se tuvieron en cuenta el costo de los recursos (incluido los conductores, los peajes, el mantenimiento de los cambios, la parte administrativa, depreciaciones, el dinero para peajes, el estacionamiento y las oficinas administrativas).
La tabla 1 muestra cómo cada una de las 6 actividades consumen recursos, es de notar que existen actividades que consumen más de un recurso y es posible que un recurso no sea consumido por una actividad específica. En las tablas 1 y 3 los recursos corresponden a: R1: Combustible, R2: Mantenimiento general, R3: Conductores, R4: Seguros, R5: Recurso administrativo, R6: Depreciaciones, R7: Dinero: R8: Espacio de oficinas y R9: Espacio de parqueo de camiones.
Tabla 1 Consumo de recurso por cada actividad
| R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | |
|---|---|---|---|---|---|---|---|---|---|
| Alistar y Despachar | 75 | 110 | |||||||
| Cargar el Camión | 205 | 205 | 205 | ||||||
| Transportar | 91.000 | 91.000 | 2.546 | 2.546 | 2.546 | ||||
| Descargar el Camión | 161 | 161 | 161 | ||||||
| Estacionar Camiones | 300 | ||||||||
| Pagar Peajes | 6.392.000 | ||||||||
| Inductor | Km | Horas | Horas | Horas | Viajes | Horas | $ | M2 | M2 |
Fuente: propia
En la tabla 1 se puede ver el inductor de recurso para cada uno de los recursos, por ejemplo, para el combustible (R1) el inductor utilizado fue el número de kilómetros recorridos, para los conductores el número de horas de trabajo, y así para todos los recursos identificados.
La tabla 2 representa el consumo de actividades por cada una de las rutas. Para las actividades alistar, despachar, cargar y descargar el camión, el inductor fue el número de viajes. Para la actividad transporte, el inductor fue el número de kilómetros, para los peajes se utilizó el porcentaje de kilómetros por ruta y para el estacionamiento el inductor fue el número de días de estacionamiento por ruta. Con esta información se aplica el modelo matricial presentado en la etapa 1, donde la información de las tablas 1 y 2 fue normalizada y se obtuvieron los resultados presentados en las tablas 3 y 4 respectivamente.
Tabla 2 Consumo de actividades por cada producto
| Alistar y Despachar | Cargar el Camión | Transportar | Descargar el Camión | Estacionar Camiones | Pagar Peajes | |
|---|---|---|---|---|---|---|
| Ruta 1 | 10 | 10 | 2.000 | 10 | 30 | 4% |
| Ruta 2 | 10 | 10 | 6.000 | 10 | 20 | 12% |
| Ruta 3 | 15 | 15 | 15.000 | 15 | 15 | 19% |
| Ruta 4 | 20 | 20 | 32.000 | 20 | 10 | 31% |
| Ruta 5 | 20 | 20 | 36.000 | 20 | 5 | 35% |
| Total | 75 | 75 | 91000 | 75 | 80 | 100% |
| Inductor | Viajes | Viajes | Kilómetros | Viajes | Días | % Km ruta |
Fuente: propia
Tabla 3 Matriz normalizada recurso-actividad
| R1 | R2 | R3 | R4 | R5 | R6 | R7 | R8 | R9 | |
|---|---|---|---|---|---|---|---|---|---|
| Alistar y Despachar | 0,00% | 0,00% | 0,00% | 0,00% | 100% | 0,00% | 0,00% | 100% | 0,00% |
| Cargar el Camión | 0,00% | 0,00% | 7,04% | 7,04% | 0,00% | 7,04% | 0,00% | 0,00% | 0,00% |
| Transportar | 100% | 100% | 87,42% | 87,42% | 0,00% | 87,42% | 0,00% | 0,00% | 0,00% |
| Descargar el Camión | 0,00% | 0,00% | 5,54% | 5,54% | 0,00% | 5,54% | 0,00% | 0,00% | 0,00% |
| Estacionar Camiones | 0,00% | 0,00% | 0,00% | 0,00% | 0,00% | 0,00% | 0,00% | 0,00% | 100% |
| Pagar Peajes | 0,00% | 0,00% | 0,00% | 0,00% | 0,00% | 0,00% | 100% | 0,00% | 0,00% |
Fuente: propia
Como se ve en la tabla 3, actualmente se está asignando el total de los recursos a cada una de las actividades identificadas, no considerando ineficiencias o tiempos muertos en el proceso, esto porque no se cuenta con dichos registros, sin embargo, en caso de estar disponible esta información el modelo permite crear actividades que representen el tiempo ocioso para determinar su costo y servir como base para la toma de decisiones en lo que respecta a la eficiencia de los procesos.
La tabla 4 permite identificar de una manera sencilla como las actividades son consumidas por cada una de las rutas. Con esta información, utilizando el modelo matricial ABC se obtiene el costo para cada una de las rutas y el costo promedio por viaje tal como se muestra en la tabla 5, el costo de las rutas guarda una estrecha relación con los kilómetros de dicha ruta.
Tabla 4 Matriz normalizada actividad-producto
| Alistar y Despachar | Cargar el Camión | Transportar | Descargar el Camión | Estacionar Camiones | Pagar Peajes | |
|---|---|---|---|---|---|---|
| Ruta 1 | 13,3% | 13,3% | 2,2% | 13,3% | 37,5% | 3,8% |
| Ruta 2 | 13,3% | 13,3% | 6,6% | 13,3% | 25,0% | 11,5% |
| Ruta 3 | 20,0% | 20,0% | 16,5% | 20,0% | 18,8% | 19,2% |
| Ruta 4 | 26,7% | 26,7% | 35,2% | 26,7% | 12,5% | 30,8% |
| Ruta 5 | 26,7% | 26,7% | 39,6% | 26,7% | 6,3% | 34,6% |
Fuente: propia
Tabla 5 Matriz actividad-producto
| Ruta | Costo Total ($) | Costo por Viaje ($) |
|---|---|---|
| Ruta 1 | 9.110.360 | 911.036 |
| Ruta 2 | 17.015.942 | 1.701.594 |
| Ruta 3 | 36.767.671 | 2.451.178 |
| Ruta 4 | 72.593.026 | 3.629.651 |
| Ruta 5 | 80.502.762 | 4.025.138 |
Fuente: propia
Teniendo en cuenta el paso 2 de la metodología, se analizó la estructura de los factores de producción que presentan variabilidad y afectan directamente el costo de cada una de las rutas, entre ellos se encuentran: los kilómetros por galón (los cuales dependen del conductor, del flujo vehicular, de condiciones técnicas y mecánicas del vehículo, del material a transportar), el tiempo de carga y de descarga del camión, y el precio del galón de combustible.
Para el paso 3, se tuvo que la organización cuenta con 400 registros de viajes realizados, los kilómetros por galón, así como el tiempo de carga y descarga de cada uno de los vehículos. Con esta información se realizó la prueba K-S para la determinación de la distribución empírica de estas variables, así como el análisis de correlaciones de estas tres variables obteniendo como resultado las tablas 6 y 7. El análisis K-S, permitió determinar que la distribución Gamma es la que mejor se ajusta a los kilómetros por galón y para modelar el tiempo de carga y descarga se recomienda una distribución Multiplicativo Beta.
En la tabla 7 se muestra que existe una fuerte correlación positiva entre el tiempo de carga y tiempo de descarga del camión. Dicha correlación se incluirá en el proceso de simulación.
Tabla 6 Ajuste de distribución de variables
| Kilometro por Galón | Tiempo de Carga | Tiempo de Descarga | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Mejor supuesto Ajustado | 6,81 | Mejor supuesto Ajustado | 2,73 | Mejor supuesto Ajustado | 2,78 | ||||||
| Distribución Ajustada Gamma | Distribución Ajustada Multiplicativo Beta | Distribución Ajustada Multiplicativo Beta | |||||||||
| Alfa | 27,07 | Ubicación | 2,00 | Ubicación | 1,88 | ||||||
| Beta | 0,25 | Factor | 1,50 | Factor | 1,90 | ||||||
| Alfa | 0,94 | Alfa | 1,55 | ||||||||
| Beta | 0,97 | Beta | 1,71 | ||||||||
| Estadístico Kolmogorov-Smirnov | 0,02 | Estadístico Kolmogorov-Smirnov | 0,02 | Estadístico Kolmogorov-Smirnov | 0,04 | ||||||
| Prueba Estadística de P-Value | 0,9962 | Prueba Estadística de P-Value | 0,9983 | Prueba Estadística de P-Value | 0,6429 | ||||||
| Real | Teórica | Real | Teórica | Real | Teórica | ||||||
| Media | 6,81 | 6,82 | Media | 2,73 | 2,74 | Media | 2,78 | 2,78 | |||
| Desviación Estándar | 1,31 | 1,31 | Desviación Estándar | 0,44 | 0,44 | Desviación Estándar | 0,46 | 0,46 | |||
| Asimetría | 0,35 | 0,38 | Asimetría | 0,05 | 0,03 | Asimetría | -0,01 | 0,08 | |||
| Curtosis | 0,29 | 0,22 | Curtosis | -1,21 | -1,22 | Curtosis | -1,14 | -0,95 | |||
Fuente: Propia
Tabla 7 matriz de correlación entre variables
| Km/Galón | Tiempo de Carga | Tiempo de Descarga | |
|---|---|---|---|
| Km/Galón | 1 | ||
| Tiempo de Carga | 0,0372 | 1 | |
| Tiempo de Descarga | 0,1016 | 0,6300 | 1 |
Fuente: Propia
Para el precio de combustible se tomó como referencia que estos pueden variar entre $7.078 y $8.776, de acuerdo con la zona geográfica del país donde se realice el tanqueo, y para este parámetro se asumió una distribución uniforme.
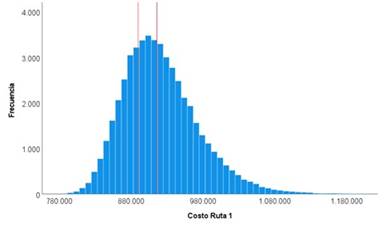
Una vez mapeados los factores, se procedió al paso 4, la obtención de resultados. Se realizó el análisis de los costos de cada una de las rutas, con un análisis de simulación Monte Carlo utilizando el Software Risk Simulator® 2019 con 50.000 simulaciones del modelo determinístico. Al realizar las simulaciones se obtuvieron posibles costos por viaje en cada una de las rutas, y con un análisis estadístico permitió establecer los límites de tolerancia para cada ruta tal como se muestra en las figuras 2 a 6, donde, las líneas de referencia marcadas en los gráficos identifican el límite superior e inferior de tolerancia de la organización, dentro de los cuales los tomadores de decisiones no deberían preocuparse.
La figura 2 muestra los posibles valores que se pueden obtener de costo por viaje en la ruta 1, los cuales pueden ir desde $757.423 a $1.264.913 lo que muestra la incidencia significativa que tiene la variabilidad de los factores de producción en el costo de la ruta 1 y en general en todas las rutas.
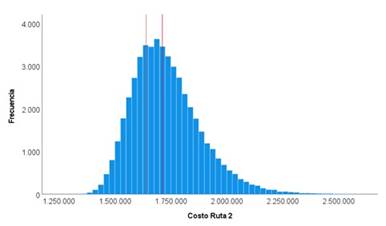
En la figura 3 se puede ver que los límites de tolerancia del costo de la ruta 2 los cuales son $1.639.571 como límite inferior y $1.712.226 como límite superior, un valor de costo entre dichos valores sería aceptable para la organización y no generaría alarmas, sin embargo, un valor por fuera de dicho rango ameritaría investigación y posiblemente acciones.
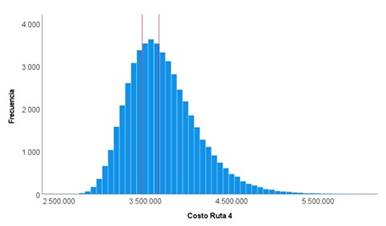
En la figura 4 se puede ver que límite inferior de la ruta 3 es $2.343.773 y el superior $2.468.502 y en la figura 5 se puede ver que límite inferior de la ruta 4 es $3.464.785 y el superior $3.657.134.
En la figura 6 se puede ver que límite inferior de la ruta 5 es $38.39.503 y el superior $4.055.763 es de destacar que entre más kilómetros tiene una ruta mayor es el rango de variación del costo por ruta.
En la figura 7 se presenta el límite de tolerancia para el costo total de las rutas el cual puede ser utilizado para análisis del cumplimiento presupuestal. En la figura 7 se puede ver la variabilidad que existe en el costo total de operación para un volumen de 400 viajes, el cual va desde $154.546.576 a $381.060.215, este rango de valores indica que las utilidades de la compañía tienen gran sensibilidad con respecto a los factores productivos, por lo que es necesario establecer procesos de control que permitan mantener el costo de las rutas dentro de los límites de tolerancia los cuales son $206.870.358 y $219.263.829.
Las estadísticas relacionadas con las figuras 2 a 7 son presentadas en la tabla 8 donde se destacan la media, mediana, desviación estándar del resultado, el rango y los límites de tolerancia inferior y superior que indican cuando el costo está dentro de los límites establecidos por la organización. Es de destacar que en todos los casos la media es mayor a la mediana lo que supone una distribución de resultados sesgada a la derecha lo que en términos de costo no es muy beneficioso para la organización pues los costos tienden más al alza que a la baja.
Para ilustrar el análisis realizado se toma la ruta número 5. Con las condiciones actuales se tiene costo promedio para la ruta de $4.002.111, este valor podría ser considerado como el valor estándar para dicha ruta, la empresa acepta una variación más o menos del 10% de su media (límite inferior y límite superior de tolerancia) esto es un valor entre $3.839.503 y 4.055.763, toda variación que esté por debajo o por encima de dicho valor debe ser investigada, en caso de estar dentro de dichos valores se acepta como dentro del control. Esto permite a los tomadores de decisiones, saber cuándo vale la pena analizar una desviación y cuándo la desviación se encuentra dentro de los límites establecidos por lo que no requiere ninguna acción.
Un aspecto interesante es que el valor estándar de cada ruta no es estático, sino que varía de acuerdo con el comportamiento de los factores de riesgo identificados, por lo que se debe correr el modelo cada cierto tiempo con los parámetros ajustados y volver a modificar el promedio esperado. Además, cada organización puede definir sus límites de tolerancia de acuerdo con factores propios del proceso de producción, o factores administrativos. La misma lógica de análisis se aplica al costo total con el fin de determinar si el resultado de un periodo está dentro de los parámetros normales de operación o no, en el caso de no cumplir con dicho rango se espera que se investigue la causa y se generen medidas de intervención con el fin de disminuir los impactos negativos adversos que un sobrecosto puede generar en la organización. Cabe destacar que la incertidumbre en la estimación de los costos puede disminuir en la medida que exista más información de la realización de un producto o la prestación de un servicio en cualquier etapa de su ciclo de vida 31.
Para los tomadores de decisiones un valor importante además de los límites de tolerancia es el rango calculado como la diferencia entre el valor máximo y el valor mínimo obtenido en la simulación. Se destaca la magnitud significativa del rango del costo total $226.513.639 el cual indica una alta sensibilidad del costo de la compañía a los cambios en los factores de producción, por lo que se debe monitorear constantemente cual de las rutas se encuentra fuera de los límites de tolerancia y generar medidas de intervención lo más rápido posible para no generar efectos adversos en las finanzas de la organización.
Tabla 8 Estadísticas básicas por Ruta
| Parámetros | Ruta 1 | Ruta 2 | Ruta 3 | Ruta 4 | Ruta 5 | Costo Total |
|---|---|---|---|---|---|---|
| Media | 908.358 | 1.693.829 | 2.438.326 | 3.609.168 | 4.002.111 | 214.822.339 |
| Mediana | 902.648 | 1.674.208 | 2.404.686 | 3.555.134 | 3.941.237 | 211.770.786 |
| Desviación | 53.347 | 153.113 | 254.309 | 406.450 | 457.194 | 23.128.468 |
| Máximo | 1.264.913 | 2.784.575 | 4.263.262 | 6.535.391 | 7.295.429 | 381.060.215 |
| Mínimo | 757.423 | 1.285.233 | 1.772.068 | 2.556.419 | 2.820.531 | 154.546.576 |
| Rango | 507.490 | 1.499.342 | 2.491.194 | 3.978.972 | 4.474.898 | 226.513.639 |
| Límite Inferior de Tolerancia | 890.073 | 1.639.571 | 2.343.773 | 3.464.785 | 3.839.503 | 206.870.358 |
| Límite Superior de Tolerancia | 916.045 | 1.712.226 | 2.468.502 | 3.657.134 | 4.055.763 | 217.263.829 |
Fuente: Propia
5. Conclusiones
Cuando se modela un fenómeno, la persona que toma la decisión debe decidir si incluir o no la incertidumbre asociada con él. Existen por lo menos dos posibilidades, realizar la aproximación a una realidad mediante un modelo determinístico donde se asume certeza en los parámetros, o en casos que la variabilidad en los procesos sea considerable, vale la pena entender el fenómeno a través de un modelo probabilístico.
En este artículo se propone un modelo matricial de costos basado en actividades que permite establecer esos límites teniendo en cuenta el proceso de producción y los factores que generan los costos. Se puede destacar del modelo el hecho de incluir las correlaciones entre los factores inciertos del proceso de producción y la utilización de técnicas estadísticas para el análisis de la información organizacional. El modelo propuesto puede ser aplicado en organizaciones donde exista incertidumbre en los factores de producción o donde existan parámetros que varíen en el tiempo. La simulación permitió obtener soluciones con un costo-beneficio adecuado.
En este caso se utilizó la simulación de Monte Carlo para medir el nivel de incertidumbre inherente en un proceso y estimar los posibles valores que podría tener el costo de prestación de un servicio y sus límites de tolerancia. Una variación de costos dentro de un rango aceptable se considera un "evento bajo control" y no requiere investigación o acción. La aplicación del modelo a un caso de estudio permitió identificar no solo el costo asociado a un producto, sino también los límites de tolerancia y el rango de variaciones del costo total durante un periodo, información que puede ser utilizada a nivel operativo para controlar el costo de cada producto, como a nivel estratégico para el control presupuestal de la organización.
En el caso de empresas de transporte, la incertidumbre en los factores de producción es clave, ya que el costo no sólo depende de elementos externos como el precio del combustible sino también internos como los tiempos de carga y de descarga, y el rendimiento en km/galón que puede estar asociado a condiciones en la vía o comportamientos del conductor. Todos estos elementos generan un costo que no es determinístico y que debe ser abordado con modelos como el presentado en este artículo que permite identificar cuando el proceso está o no controlado y generar las respectivas medidas de intervención.
Los responsables de la toma de decisiones analizan las variaciones para evaluar el desempeño después de la implementación de las decisiones, con el fin de activar el proceso de aprendizaje sobre el comportamiento de costos de la organización y realizar mejoras continuas. En la era de los grandes datos, la inteligencia artificial, el aprendizaje automático y la analítica empresarial, se debe hacer antes de que se produzcan los costos, apoyando la analítica predictiva eficaz en la práctica, aquí la simulación de Monte Carlo puede ser considerada una herramienta apropiada para dicho análisis.
Como trabajos futuros se planea aplicar esta metodología en sectores donde existe variabilidad innata en los procesos tales como el sector de la salud y el sector de la agricultura. Además, el artículo no considera análisis de tornado el cual permite identificar las variables clave en la variabilidad del costo total y puede ser considerado en un próximo artículo. Otro trabajo futuro es considerar los precios de venta para analizar el riesgo a nivel de la utilidad o de indicadores financieros clave para la organización.