Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
TecnoLógicas
Print version ISSN 0123-7799On-line version ISSN 2256-5337
TecnoL. vol.19 no.37 Medellín July/Dec. 2016
Artículo de investigación/Research article
Planeamiento AC de la expansión de la red de transmisión considerando repotenciación de circuitos y ubicación de capacitores
AC transmission network expansion planning considering circuits repowering and location of capacitors
Jaime A. López-López1, Diego A. Tejada-Arango2 y Jesús M. López-Lezama3
1 Ing. Electricista, Dirección Programación de la Operación XM S.A. E.S.P, Medellín-Colombia, jalopez@xm.com.co
2 M.Sc. en Ingeniería, Instituto de Investigación Tecnológica, Universidad Pontificia Comillas, Madrid-España, diego.tejada@iit.comillas.edu
3 Ph.D. en Ingeniería Eléctrica, Dpto. de Ingeniería Eléctrica, Facultad de Ingeniería, Universidad de Antioquia, Medellín-Colombia, jmaria.lopez@udea.edu.co
Fecha de recepción: 23 de noviembre de 2015/ Fecha de aceptación: 4 de mayo de 2016
Como citar / How to cite
J.A. López-López, D.A. Tejada-Arango y J.M. López-Lezama, "Planeamiento AC de la expansión de la red de transmisión considerando repotenciación de circuitos y ubicación de capacitores", Tecno Lógicas, vol. 19, no. 37, pp. 61-77, 2016
Resumen
En este artículo se aborda el problema de Planeamiento de la Expansión de la Red de Transmisión (PERT). El PERT consiste en determinar el conjunto de nuevos circuitos necesarios en un sistema de potencia, para atender una demanda futura. En su versión clásica, el PERT considera como candidatos de solución únicamente la adición de nuevas líneas y transformadores. La principal contribución de este artículo consiste en la inclusión de candidatos de solución no convencionales en el PERT. Dichos candidatos de solución son la repotenciación de circuitos existentes y la ubicación de bancos de capacitores. Para tener en cuenta estos últimos, se considera un modelo AC de la red de transmisión. La solución al modelo propuesto es llevada a cabo mediante un Algoritmo Genético Híbrido. Los resultados obtenidos son contrastados y validados con publicaciones previas de la literatura técnica. Los sistemas de prueba utilizados son el sistema Garver y el sistema IEEE de 24 barras. Los resultados obtenidos en ambos sistemas muestran que la inclusión de los candidatos no convencionales propuestos en este artículo permite disminuir los costos de la expansión de la red. Este hecho puede servir como indicador para que el planeador del sistema contemple nuevas posibilidades en los estudios de expansión.
Palabras clave: Algoritmos genéticos, planeamiento de la transmisión, programación matemática, repotenciación de líneas, ubicación de capacitores
Abstract
This paper deals with the Transmission Network Expansion Planning (TNEP) problem. The TNEP consists of finding a set of new circuits on a power system, which is needed to attend a future demand. In its classical version, the TNEP only considers as solution candidates the addition of new lines and transformers. The main contribution of this paper consists in the inclusion of non-conventional solution candidates, namely the repowering of existing circuits and the location of capacitor banks. To take into account these last ones an AC model of the transmission network is considered. The solution of the proposed model is carried out using a Hybrid Genetic Algorithm. Results are compared and validated with previous works in the technical literature. The test systems used are the Garver system and IEEE 24 bus system. The results obtained in both systems showed that the inclusion of the non-conventional candidates, proposed in this paper, allows to reduce the cost of network expansion. This fact may be useful as an indicator for the system planner to consider new possibilities in the expansion studies.
Keywords: Genetic algorithms, transmission planning, mathematical programming, line repowering, location of capacitors.
1. Introducción
El Planeamiento de Expansión de la Red de Transmisión (PERT), en su versión clásica, consiste en identificar un conjunto de nuevos elementos que deben ser incorporados a la red de transmisión, de tal modo que se atienda la demanda futura a mínimo costo. Dichos elementos son comúnmente líneas y transformadores. Sin embargo, dadas las crecientes restricciones ambientales, cada vez es más difícil acceder a espacio disponible para la construcción de nuevas líneas de transmisión. En este contexto, la repotenciación de redes existentes y ubicación de capacitores constituyen opciones atractivas para el problema del PERT. Algunas aplicaciones del uso de repotenciación como solución de la expansión de la red en sistemas reales son reportadas en [1],[2].
El modelo matemático del PERT más aproximado a la realidad, corresponde a un problema de programación no lineal entero mixto. Es decir, involucra funciones no lineales, como también variables reales y enteras. Numerosas publicaciones se han enfocado en mostrar los diferentes modelos para la representación del PERT. En [3] se ilustran el modelo de transporte, modelo DC, modelo híbrido y modelo disyuntivo. Por otro lado, el modelo AC ha sido explorado en [4],[5].
Al simplificar el PERT se puede obtener un modelo que pueda ser abordado usando programación matemática clásica (programación lineal, programación no lineal, programación lineal entera mixta, programación cuadrática y programación dinámica). Algunas contribuciones a la solución del PERT usando programación matemática clásica, sobre las cuales se pueden con-sultar en [6] - [9].
Por otro lado, el PERT también ha sido abordado mediante técnicas heurísticas, metaheurísticas y versiones híbridas de estas últimas. Dentro de las técnicas metaheurístias se destacan los Algoritmos Genéticos, Búsqueda Tabú, y Enjambre de Partículas, como puede encontrarse en [10] - [14].
A pesar de que en la literatura técnica se han propuesto muchas metodologías para abordar el problema del PERT [15], [16], todavía no se ha incorporado, de forma explícita en los modelos de optimización, la posibilidad de incluir candidatos no convencionales como repotenciación de circuitos y ubicación de capacitores. Sin embargo, existen trabajos en los que se considera la inclusión de compensación serie en circuitos existentes o el cambio de nivel de tensión en ciertos circuitos para el PERT, como se propone en [17] - [19].
El aporte principal de este artículo es el modelamiento de este tipo de candidatos en una versión AC del PERT. Los resultados obtenidos muestran que la inclusión de estos nuevos candidatos, en ocasiones, puede contribuir con opciones de expansión de menor costo para la solución del PERT.
2. Nomenclatura
Para mayor claridad, la nomenclatura usada en el modelo se presenta en la Tabla 1.
3. Formulación Matemática AC del Pert
El modelo AC para el PERT (reportado en [4], [5], está dado por las ecuaciones (1) - (10) y se ilustra a continuación.
La Ec. (1) representa la función objetivo, que en ese caso consiste en minimizar el costo de inversión v, expresado como la multiplicación del vector de costos transpuesto (cT) por el número de circuitos agregado (n). Las restricciones (2) y (3) representan los balances nodales de potencias activa y reactiva, respectivamente. Note que estas expresiones, como se especifica más adelante, están dadas mediante el modelo AC de la red.
Las restricciones (4) y (5) representan los límites mínimos y máximos de generación de potencia activa, y reactiva, respectivamente. La restricción (6) indica los límites mínimos y máximos de la magnitud de tensión en todos los nodos del sistema. Las restricciones (7) y (8) representan los límites de potencia aparente en la red. Estos tienen en cuenta los circuitos actuales y los nuevos circuitos agregados. La restricción (9) indica el número máximo de circuitos a ser agregado y finalmente, la restricción (10) indica la naturaleza de n y θ. Los elementos de los vectores de inyección de potencia P(V,θ,n) y Q(V,θ,n) son calculados mediante (11) y (12), respectivamente.
Donde i, j ∈ N, son índices que representan las barras y N es el conjunto de todas las barras; i, j, representan el circuito entre la barra i y la barra j. θij = θi - θj representa la diferencia angular entre la barra i y la barra j. Los elementos de la matriz de admitancias (G y B) están dados por (13) y (14).
Donde Ωi, representa el conjunto de todos los buses directamente conectados al bus i. Note que en (14), se considera la posibilidad de adicionar un circuito nuevo (línea o transformador) en paralelo con uno existente (en el caso base), aunque los parámetros del circuito equivalente pueden ser diferentes. En este caso, las derivaciones de los transformadores no son considerados. Tanto las líneas de transmisión como los transformadores tienen circuitos equivalentes similares.
Los elementos (i-j) de los vectores Sfrom y Sto son obtenidos a partir de las ecuaciones (15)-(20).El modelo descrito anteriormente representa un problema de Programación no Lineal Entero Mixto (PNLEM), de alta complejidad, pues es no convexo y presenta múltiples óptimos locales (multimodal) y explosión combinatorial. En la literatura especializada, el PERT es comúnmente abordado aplicando simplificaciones a las ecuaciones de balance de potencia y flujo de carga (modelo DC), ignorando el efecto de la potencia reactiva y la variación de las tensiones en la red. Estas simplificaciones dan lugar a un modelo de Programación Lineal Entero Mixto (PLEM), que puede ser abordado mediante técnicas de optimización matemática clásica que garantizan, en la mayoría de los casos, la obtención de un óptimo global en un tiempo finito.
Se debe aclarar que la obtención de tal óptimo depende en gran medida de las características y complejidad del problema bajo estudio; es decir, el tamaño, nivel de radialidad, cantidad de candidatos, posibles combinaciones de soluciones factibles, entre otros. La inclusión de estos aspectos conlleva a un modelo matemático más complejo y un mayor esfuerzo computacional. En este artículo hemos querido abordar el modelo AC, que, si bien es más complejo, puede entregar soluciones más aproximadas a la realidad (especialmente en el corto y mediano plazo del planeamiento). Por lo tanto, se ha optado por la utilización de una metaheurística como técnica de solución del modelo propuesto.
4. Metodología propuesta
Para hallar la solución que representa el menor costo para el problema del PERT, se utiliza un Algoritmo Genético Híbrido (AGH). La implementación se realizó en MATLAB, usando como sub-rutina para calcular los flujos de potencia el paquete de archivos MATPOWER [20]. Para efectos de presentar el detalle del AGH a continuación se utiliza el sistema de prueba Garver; no obstante, la implementación del sistema IEEE de 24 barras es similar.
4.1 Codificación
En la Fig. 1 se presenta la codificación utilizada usando como ejemplo los parámetros del sistema Garver [21] (los parámetros del sistema IEEE de 24 barras pueden ser consultados en [5]). La codificación se basa en un vector de 18 bits. Los primeros 15 bits corresponden a los corredores del sistema. El contenido de las casillas indica el número de circuitos en el corredor correspondiente. Los 3 bits finales indican los nodos 2, 4 y 5, donde es posible ubicar bancos de capacitores. El contenido de la casilla correspondiente, indica el número de pasos a los cuales se ajusta el banco de capacitores
.Los primeros 15 bits, enteros de 0 a 5, indican el número de circuitos en el corredor correspondiente. Por ejemplo, observe que en los corredores 1-5 y 2-3 existe solo una línea. Los enteros 6 7 y 8, indican el número de circuitos repotenciados que pueden ser 1, 2 o 3, respectivamente.
Por ejemplo, en el corredor 1-2 se indica que hay 2 circuitos repotenciados. La repotenciación de circuitos solo es considerada como una opción de expansión en los corredores donde originalmente hay líneas. En el sistema Garver estos son los corredores 1-2, 1-4, 1-5, 2-3, 2-4 y 3-5, los cuales se han marcado con asterisco. Note que estas casillas no po-drán tomar valores iguales a cero, ya que por definición poseen circuitos.
La codificación descrita anteriormente se ha hecho con base en el sistema de prueba de Garver reportado en [21], el cual ha sido utilizado de forma recurrente por diversos académicos para probar nuevos modelos y métodos de solución del PERT. Sin embargo, la codificación se puede escalar para representar cualquier otro sistema (por ejemplo, para el sistema IEEE de 24 barras). Los primeros bits representarían el número de corredores donde ubicar nuevos circuitos y los últimos, el número de barras donde es posible ubicar bancos de capacitores.
4.2 Función Objetivo
Cada una de las posibles soluciones del PERT tiene un costo asociado. Este costo es de-terminado por el número de líneas o circuitos, normales o repotenciados, y el número de bancos de capacitores que sea necesario adicionar, como se muestra en la Ec. (21).
Para la validación de resultados, los costos de las nuevas líneas son tomados de las referencias [4] y [21], donde estos se dan en unidades monetarias relativas (para el sistema IEEE de 24 barras, los costos también pueden ser consultados en [5]). Para el caso de repotenciación de líneas se asume un costo relativo igual a la mitad del costo de instalar nuevos circuitos.
Esto se da porque en la repotenciación se puede utilizar la misma servidumbre de la línea original, evitando adquisición de nuevos predios. Adicionalmente, para una línea repotenciada los valores de resistencia y reactancia se reducen a la mitad y su capacidad de transmisión es duplicada. En la Tabla 2 se indican los parámetros utilizados para los bancos de capacitores. De igual forma que para las líneas, el costo de los capacitores se da en unidades monetarias relativas.
4.3 Población inicial
Primero es generado un individuo o vector que representa una solución factible del PERT. Este es obtenido a partir de la topología inicial (en la mayoría de los casos el flujo de carga AC no converge), adicionando aleatoriamente líneas nuevas o repotenciadas, hasta que el individuo permita la convergencia del flujo de carga AC.
Finalmente, a partir de este individuo inicial factible, se procede a generar la población inicial con movimientos aleatorios en uno de los bits de este vector. Es importante mencionar que, mediante un algoritmo de comprobación, se garantiza que todos los individuos de la población son diferentes, lo que permite explorar un mayor espacio de soluciones. Adicionalmente, luego de realizar los movimientos aleatorios se comprueba la factibilidad de cada uno de los individuos de la población inicial, descartando los individuos que no cumplan esta condición.
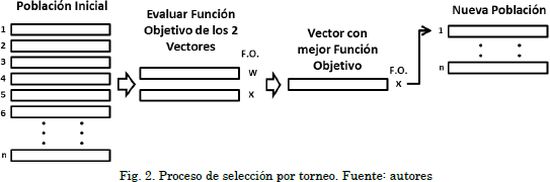
4.4 Selección por torneo
El proceso de selección por torneo consiste en tomar dos individuos de la población, evaluar su función objetivo y determinar cuál de los dos posee la mejor. Este individuo es posteriormente ingresado a una nueva población. El número de torneos realizado es n (igual tamaño que la población inicial). Este proceso se ilustra en la Fig. 2. En este proceso el mismo individuo puede eventualmente participar en más de un torneo. Sin embargo, la probabilidad de que esto ocurra es baja puesto que solo se toman dos individuos por torneo.
4.5 Recombinación
Partiendo de la nueva población generada en el paso anterior, se lleva a cabo el proceso de recombinación, el cual consiste en generar dos nuevos individuos a partir del material genético de dos padres, como se ilustra en la Fig. 3. En este caso la recombinación se hace en un solo punto, seleccionado al azar. El número de veces que se realiza la recombinación es n/2, tomando pares de individuos de la nueva población, generando una población recombinada de tamaño n.
4.6 Mutación - Búsqueda local
En el proceso de mutación se activa con una probabilidad del 50%, y consiste en realizar una búsqueda local, la cual busca mejores soluciones para cada una de las generaciones del AGH, asegurando que el algoritmo pueda converger a una solución de alta calidad. En este caso se modifica el valor de cada uno de los bits de izquierda a derecha, como se indica a continuación:
Antes de iniciar la búsqueda local se evalúa la función objetivo del vector actual y se almacena esta información como referencia. Adicionalmente, se tiene un operador "w", el cual toma los valores w = {0, 1, 2}. El valor 0 indica la reducción de una línea en el corredor que se está evaluando. El valor 1 indica la adición de una línea. El valor 2 indica que se debe evaluar la repotenciación para el corredor que se está evaluando, si este posee circuitos existentes en el caso base. En cada uno de los bits del vector (excepto en los correspondientes a los capacitores) es evaluado el operador "w" (se recorren sus 3 valores)
Para el caso de los capacitores, el valor del bit es cambiado por uno nuevo, al azar, en el rango entre 0 y 5. Cada vez que se realiza un cambio, se evalúa nuevamente la función objetivo, con el fin de determinar si esta mejora. El proceso es realizado de esta forma para enfocar la búsqueda local en reducir el número de líneas, evaluar la repotenciación y la ubicación de capacitores como posibles candidatos de solución. Una vez se termina la búsqueda local, se almacena el mejor individuo encontrado.
5. Pruebas y resultados
Para calibrar los parámetros del AGH, se realizaron varios ensayos modificando el tamaño de la población, el número de torneos y la probabilidad de mutación. Los datos ajustados, mediante análisis de sensibilidad, que arrojaron mejores resultados se ilustran en la Tabla 3. En este caso en particular se encontraron resultados satisfactorios con los mismos parámetros para ambos sistemas de prueba. Sin embargo, vale la pena mencionar que el proceso de parametrización de las técnicas metaheurísticas puede variar de un sistema a otro.
Los resultados obtenidos con el AGH fueron contrastados y validados con dos publicaciones de la literatura técnica (sistema Garver).
El primer caso de validación se realiza con la publicación original de Garver [21]; el segundo caso se realiza con el mismo sistema, pero adoptando las modificaciones de red propuestas en [4]. Adicionalmente, son presentados resultados obtenidos al implementar el AGH para el sistema IEEE de 24 barras.
5.1 Primer caso de validación - Sistema Garver
Inicialmente, para reproducir los resultados reportados en [21], no se tienen en cuenta la repotenciación de circuitos ni la ubicación de condensadores. En la Fig. 4 se ilustra la mejor solución obtenida por el AGH que coincide con la reportada en [21]. En este caso se indica la adición de 1 línea en 3-5, 4 líneas en 2-6 y 2 líneas en 4-6, para un costo de US$ 200. En la Fig. 5 se ilustra el sistema de potencia con la solución implementada.
Posteriormente se incluyen como candidatos de solución la repotenciación de circuitos y la ubicación de bancos de capacitores, obteniendo el resultado ilustrado en la Fig. 6.
Esta muestra la repotenciación del circuito descrito en 3-5, la adición de 4 líneas en 2-6 y 2 líneas en 4-6, con un costo de US$ 190. En la Fig. 7 se ilustra el sistema de potencia con la solución implementada. Se puede observar que para el primer caso de validación la inclusión de candidatos no convencionales en el PERT conduce a una reducción del costo equivalente a US$ 10. En este caso la mejor solución encontrada no incluye la ubicación de bancos de condensadores como componentes del vector solución.
5.2 Segundo caso de validación - Sistema Garver
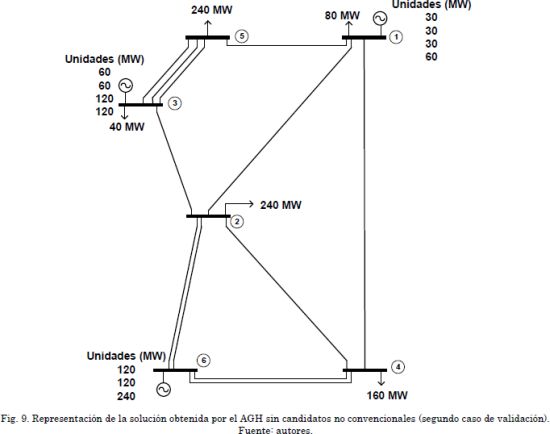
Para el segundo caso de validación se ajustaron los costos según indicado en [4] y se ajustó el PERT considerando redespacho. Inicialmente no se tuvo en cuenta la repotenciación ni los bancos de capacitores, llegando al mismo resultado reportado en [4]. Esta solución es ilustrada en la Fig. 8. En este caso es necesaria la adición de 2 líneas en 3-5, 2 líneas en 2-6 y 2 líneas en 4-6, para un costo de US$ 160. En la Fig. 9 se ilustra el sistema de potencia con la solución implementada.
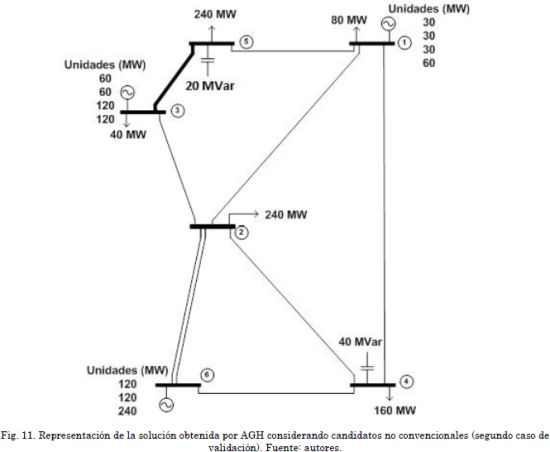
Posteriormente, se considera la opción de repotenciación y ubicación de bancos de capacitores, obteniendo la solución ilustrada en la Fig. 10, la cual indica 1 circuito repotenciado en 3-5, la adición de 2 líneas en 2-6, 1 línea en el corredor 4-6, 1 banco de capacitores de 2 pasos (40 MVar) en el nodo 4 y 1 banco de capacitores de 1 paso (20 MVar) en el nodo 5, para un costo de US$ 106. En la Fig. 11 se ilustra el sistema de potencia con la solución implementada. En este caso se obtiene una reducción del costo del PERT de US$ 54 debido a la inclusión de candidatos no convencionales.
5.3 Sistema IEEE de 24 barras
Como se mencionó anteriormente los datos de este sistema pueden ser consultados en [5] . Para la repotenciación de líneas se asume un costo relativo igual a la mitad del costo de instalar nuevos circuitos. Para una línea repotenciada los valores de resistencia y reactancia se reducen a la mitad y su capacidad de transmisión es duplicada. Adicionalmente, se tienen las siguientes consideraciones:
La repotenciación solo se realiza a un máximo de líneas que está determinado por el número de las existentes en el caso base.
Es posible tener en cada uno de los corredores un máximo de 3 líneas (nuevas más existentes).
Inicialmente, no se tienen en cuenta la repotenciación de circuitos ni la ubicación de capacitores (esto se hace asignando de forma artificial costos altos a estos candidatos). En la Fig. 12 se ilustra la mejor solución obtenida por el AGH para el sistema IEEE de 24 barras.
En este caso se indica la adición de 1 línea en los corredores en 3-24, 12-13, 14-23, 15-16 y 15-24, 2 líneas en 6-10 y 7-8, para un costo de US$362 x 106. Los resultados son consistentes con los reportados en [5], [22], [23]; en especial con respecto a los corredores en los cuales el AGH adiciona nuevas líneas de transmisión. La no exactitud en resultados obtenidos para este sistema, respecto a las publicaciones mencionadas anteriormente se debe a diferencias en el modelo AC/DC, metodologías utilizadas y candidatos de solución empleados. En la Fig. 13 se ilustra el sistema de potencia con la solución implementada.
Posteriormente se incluyen como candidatos de solución la repotenciación de circuitos existentes y la ubicación de capacitores. Los resultados obtenidos se ilustran en la Fig. 14. Este indica la repotenciación (línea más gruesa) de los circuitos existentes en 2-4, 3-24, 7-8, 9-12, 11-13 y la adición de 1 línea en 6-10, dos capacitores de 100 MVar (5 pasos de 20 MVar) en los nodos 3, 10, y uno más de 60 MVar en el nodo 8 (3 pasos de 20 MVar), con un costo de US$ 149,5 x 106. En la Fig. 15 se ilustra el sistema de potencia con la solución implementada. Se puede observar que al realizar la inclusión de candidatos no convencionales en el PERT se genera una reducción del costo, equivalente a US$ 212,5 x 106.
6. Conclusiones
El principal aporte de este trabajo es la introducción de candidatos no convencionales (repotenciación de circuitos y ubicación de capacitores) para la solución del PERT. Además, el uso de un modelo AC como representación de la red, permite tener un mayor acercamiento a los fenómenos reales presentes en los sistemas eléctricos de potencia.
Al incluir candidatos no convencionales en la solución del PERT es posible explorar un conjunto mayor de posibles soluciones y encontrar nuevas alternativas de expansión que involucran menores costos.
La validación de los resultados obtenidos por el AGH propuesto fue satisfactoria, al encontrar y mejorar las soluciones para el problema del PERT que han sido reportadas previamente en la literatura. En un trabajo futuro se pretende incluir otro tipo de soluciones no convencionales como la reconfiguración de la red existente y la inclusión de transformadores tridevanados, además de otras técnicas metaheurísticas para la búsqueda de soluciones de alta calidad.
7. Agradecimientos
Los autores agradecen el apoyo del Proyecto de Sostenibilidad 2016-2017 de la Universidad de Antioquia.
Referencias
[1] C. de O. E. del S. I. N. (COES), “Informe DP-01-2012: Propuesta de la Actualización del Plan de Transmisión 2013 - 2022,” techreport, 2012. [ Links ]
[2] E. T. A., Antonio Sertich K., Armando Ortiz T., “Estudio de repotenciación de las líneas de transmisión Itaipú - Margen Derecha en 500kV con conductores Termoresistentes,” techreport, 2009. [ Links ]
[3] G. Latorre, R. D. Cruz, J. M. Areiza, and A. Villegas, “Classification of publications and models on transmission expansion planning,” IEEE Trans. Power Syst., vol. 18, no. 2, pp. 938-946, May 2003. [ Links ]
[4] M. J. Rider, A. V. García, and R. Romero, “A constructive heuristic algorithm to short term transmission network expansion planning,” in IEEE Power Engineering Society General Meeting 2004, vol. 2, pp. 2108-2114, 2004. [ Links ]
[5] M. J. Rider, A. V. García, and R. Romero, “Power system transmission network expansion planning using AC model,” IET Gener. Transm. Distrib., vol. 1, no. 5, p. 731, 2007. [ Links ]
[6] S. Binato, M. V. F. Pereira, and S. Granville, “A new Benders decomposition approach to solve power transmission network design problems,” IEEE Trans. Power Syst., vol. 16, no. 2, pp. 235-240, May 2001. [ Links ]
[7] L. Bahiense, G. C. Oliveira, M. Pereira, and S. Granville, “A mixed integer disjunctive model for transmission network expansion,” IEEE Trans. Power Syst., vol. 16, no. 3, pp. 560-565, 2001. [ Links ]
[8] E. Carreno, E. N. Asada, R. Romero, and A. V García, “A branch and bound algorithm using the hybrid linear model in the transmission network expansion planning,” in 2005 IEEE Russia Power Tech, pp. 1-6, 2005, [ Links ].
[9] A. S. D. Braga and J. T. Saraiva, “A Multiyear Dynamic Approach for Transmission Expansion Planning and Long-Term Marginal Costs Computation,” IEEE Trans. Power Syst., vol. 20, no. 3, pp. 1631-1639, Aug. 2005. [ Links ]
[10] A. M. Leite da Silva, L. S. Rezende, L. M. Honório, and L. A. F. Manso, “Performance comparison of metaheuristics to solve the multi-stage transmission expansion planning problem,” IET Gener. Transm. Distrib., vol. 5, no. 3, p. 360, 2011. [ Links ]
[11] R. A. Gallego, A. B. Alves, A. Monticelli, and R. Romero, “Parallel simulated annealing applied to long term transmission network expansion planning,” IEEE Trans. Power Syst., vol. 12, no. 1, pp. 181-188, 1997. [ Links ]
[12] E. L. Da Silva, J. M. A. Ortiz, G. C. De Oliveira, and S. Binato, “Transmission network expansion planning under a Tabu Search approach,” IEEE Trans. Power Syst., vol. 16, no. 1, pp. 62-68, 2001. [ Links ]
[13] D. Kavitha and K. S. Swarup, “Transmission Expansion Planning Using LP-Based Particle Swarm Optimization,” in 2006 IEEE Power India Conference, pp. 207-212, 2006. [ Links ]
[14] A. Verma, B. K. Panigrahi, and P. R. Bijwe, “Harmony search algorithm for transmission network expansion planning,” IET Gener. Transm. Distrib., vol. 4, no. 6, p. 663, 2010. [ Links ]
[15] A. R. Abbasi and A. R. Seifi, “Unified electrical and thermal energy expansion planning with considering network reconfiguration,” IET Gener. Transm. Distrib., vol. 9, no. 6, pp. 592-601, Apr. 2015. [ Links ]
[16] S. Heidari, M. Fotuhi-Firuzabad, and S. Kazemi, “Power Distribution Network Expansion Planning Considering Distribution Automation,” IEEE Trans. Power Syst., vol. 30, no. 3, pp. 1261-1269, May 2015. [ Links ]
[17] M. Rahmani, G. Vinasco, M. J. Rider, R. Romero, and P. M. Pardalos, “Multistage Transmission Expansion Planning Considering Fixed Series Compensation Allocation,” IEEE Trans. Power Syst., vol. 28, no. 4, pp. 3795-3805, Nov. 2013. [ Links ]
[18] G. Vinasco, M. J. Rider, and R. Romero, “A Strategy to Solve the Multistage Transmission Expansion Planning Problem,” IEEE Trans. Power Syst., vol. 26, no. 4, pp. 2574-2576, Nov. 2011. [ Links ]
[19] A. H. Dominguez, A. Escobar Z., and R. A. Gallego, “Transmission expansion planning considering conductor proposals with different wire size and technology,” in 2014 IEEE PES Transmission & Distribution Conference and Exposition - Latin America (PES T&D-LA), pp. 1-6, 2014, [ Links ].
[20] R. D. Zimmerman, C. E. Murillo-Sánchez, and R. J. Thomas, “MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education,” IEEE Trans. Power Syst., vol. 26, no. 1, pp. 12-19, Feb. 2011. [ Links ]
[21] L. Garver, “Transmission Network Estimation Using Linear Programming,” IEEE Trans. Power Appar. Syst., vol. PAS-89, no. 7, pp. 1688-1697, Sep. 1970. [ Links ]
[22] Risheng Fang and D. J. Hill, “A new strategy for transmission expansion in competitive electricity markets,” IEEE Trans. Power Syst., vol. 18, no. 1, pp. 374-380, Feb. 2003. [ Links ]
[23] R. Romero, C. Rocha, J. R. S. Mantovani, and I. G. Sánchez, “Constructive heuristic algorithm for the DC model in network transmission expansion planning,” IEE Proc. - Gener. Transm. Distrib., vol. 152, no. 2, p. 277, 2005. [ Links ]