Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
TecnoLógicas
Print version ISSN 0123-7799On-line version ISSN 2256-5337
TecnoL. vol.20 no.40 Medellín Dec. 2017
Artículo de investigación/Research article
Propiedades Piezoeléctricas del Pentóxido de Niobio y Pentóxido de Tantalio: un estudio desde primeros principios
A first-principles study of the piezoelectric properties of Niobium and Tantalum Pentoxides
Olga M. Giraldo-Giraldo1, Santiago Pérez-Walton2, y Jorge M. Osorio-Guillén3
1 Física, Universidad de Antioquia UdeA, Medellín-Colombia, omargarita.giraldo@udea.edu.co
2 PhD. en Física, M.Sc. en Física, Físico, Departamento de Electrónica, Instituto Tecnológico Metropolitano, Medellín-Colombia, santiagoperez@itm.edu.co
3 PhD. en Física, M.Sc. en Física, Físico, Universidad de Antioquia UdeA, Medellín-Colombia, mario.osorio@udea.edu.co
Fecha de recepción:14 de diciembre de 2016/ Fecha de aceptación: 24 de julio de 2017
Como citar / How to cite
O. M. Giraldo-Giraldo, S. Pérez-Walton, y J. M. Osorio-Guillén, Propiedades Piezoeléctricas del Pentóxido de Niobio y Pentóxido de Tantalio: un estudio desde primeros principios. TecnoLógicas, vol. 20, no. 40, pp. 43-51, 2017.
Resumen
Nb2O5 y Ta2O5 son óxidos semiconductores de brecha ancha, los cuales en los últimos años han despertado gran interés debido a sus múltiples aplicaciones tecnológicas, ya sea en electrónica, telecomunicaciones o fotocatálisis. Por estas razones, en este trabajo presentamos un estudio a partir de cálculos de primeros principios de las propiedades piezoeléctricas de las fases Z y β de Ta2O5, y de las fases Z y P de Nb2O5 utilizado la teoría de los funcionales de la densidad y la aproximación del gradiente, generalizado con la parametrización PBEsol. Una vez determinada la geometría de equilibrio para cada una de estas fases, realizamos un cálculo utilizando respuesta lineal para determinar el tensor piezoeléctrico asociado a cada una de estas fases, encontrando que la fase Z para ambos compuestos presenta una buena respuesta piezoeléctrica. Adicionalmente, encontramos que la fase β-Ta2O5 no presenta respuesta piezoeléctrica.
Palabras clave: Piezoelectricidad, semiconductores de brecha ancha, Nb2O5, Ta2O5, primeros principios.
Abstract
Nb2O5 and Ta2O5 are wide-bandgap semiconductor oxides that have attracted great interest in recent years due to their technological applications, such as in electronics, telecommunications or photocatalysis. Because of this, we present a study based on first-principles calculations of the piezoelectric properties of the Z and β phases of Ta2O5 as well as the Z and P phases of Nb2O5 by using the Density Functional Theory and the Generalized Gradient Approximation with PBEsol parameterization. Once the equilibrium geometry was determined for each of these phases, we made a calculation using the linear response theory to determine the piezoelectric tensor associated with each phase. We discovered that the Z phase of both compounds presents good piezoelectric response. Additionally, β-Ta2O5 does not show such response.
Keywords: Piezoelectricity, wide-bandgap semiconductors, Nb2O5, Ta2O5, first-principles.
1. Introducción
El pentóxido de Niobio (Nb2O5) y el pentóxido de Tantalio (Ta2O5) son óxidos semiconductores de brecha ancha que en los últimos años han motivado una gran cantidad de estudios, tanto experimentales como teóricos, debido a la gran variedad de aplicaciones que tienen en el ámbito tecnológico e industrial. Por ejemplo, Nb2O5 es muy usado en el sector aeroespacial, donde es utilizado en la fabricación de micro capacitores [1]; mientras que la alta estabilidad química, alto índice de refracción y bajo coeficiente de absorción, hacen que Ta2O5 pueda ser usado en la fabricación de capacitores de películas delgadas y en cubiertas anti reflectivas para celdas solares [2].
Hasta hace poco tiempo, el diagrama de fase para ambos compuestos era una incógnita. Sin embargo, recientes estudios teóricos lograron establecer las fases energética y dinámicamente más estables para Nb2O5 y Ta2O5 [3], [4]. En general, las fases (estables o meta estable) de estos compuestos presentan propiedades físicas muy interesantes, como una gran constante dieléctrica e interesantes propiedades piezoeléctricas. Sin embargo, no todas las fases de estos compuestos presentan propiedades piezoeléctricas, ya que de acuerdo con la simetría puntual asociada a cada una de las fases, se puede identificar que solamente una parte de estas, con grupo puntual no-centro simétrico, presentan estas propiedades, entre las que podemos destacar P y Z para Nb2O5 [3], [5], Z y β (modelo Ramprasad) para Ta2O5 [6], [7]. Debido a la gran importancia de la piezoelectricidad a nivel industrial, estudios experimentales en películas delgadas de Ta2O5 usando técnicas de pulverización, reportaron que las películas delgadas de Ta2O5 con estructura monoclínica pertenecientes al grupo puntual m, exhiben propiedades piezoeléctricas comparables a ZnO [2], [8], [9], [10].
Por otro lado, el estudio de las propiedades físicas de un material por medio de técnicas experimentales está algunas veces limitado por la disponibilidad del material, la pureza cristalina del compuesto sintetizado, el método y montaje experimental, el tiempo de fabricación y medición, etc. En estos casos, los métodos teóricos, tales como las simulaciones atomistas por medio de primeros principios son una alternativa que no presenta este tipo de limitaciones y que pueden predecir adecuadamente el comportamiento de nuevos materiales u otras propiedades emergentes que hasta el momento no han sido identificadas experimentalmente [11]. La teoría de los funcionales de la densidad es el único método existente que permite hacer este tipo de exploración sin la necesidad de parámetros ajustables a datos experimentales, que en muchos casos pueden presentar otros métodos teóricos [12].
Por las razones anteriores, en este trabajo realizamos un estudio exhaustivo de las propiedades piezoeléctricas de las fases Z y P de Nb2O5, Z y β (modelo Ramprasad) de Ta2O5 a partir de cálculos de primeros principios, usando la teoría de los funcionales de la densidad, y comparamos indirectamente nuestros resultados con los valores reportados para dos materiales que presentan interesantes respuestas piezoeléctricas: ZnO y BiTiO3.
2. Materiales y métodos
2.1 Tensor piezoeléctricoa
Si un dieléctrico es sometido a compresiones o elongaciones, la polarización en el material cambia, de tal manera que se genera una diferencia de potencial y en un circuito cerrado, se podría medir una corriente eléctrica. De la misma manera, si el dieléctrico se coloca en presencia de un campo eléctrico externo, el centro de masa de los momentos dipolares en el material cambia, de tal manera que el material experimenta deformaciones. A partir de estos dos fenómenos, se puede definir el tensor piezoeléctrico de la siguiente manera:
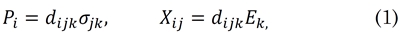
donde la polarización eléctrica P1 y el campo eléctrico Ek son tensores de rango 1, la tensión σjk y la deformación Xij son tensores de rango 2 y el tensor piezoeléctrico dijk , es un tensor de rango 3 (aquí estamos utilizando la convención de Einstein, donde se tiene una suma sobre índices repetidos). Debido a que el tensor de tensiones σjk es un tensor simétrico, entonces las 27 componentes del tensor piezoeléctrico pueden reducirse a 18 componentes independientes. En forma matricial, el tensor piezoeléctrico puede escribirse entonces de la siguiente manera:

De los 32 grupos puntuales, únicamente los grupos no-centro simétricos presentan piezoelectricidad. En la Tabla 1, se presenta una lista de los sistemas cristalinos y sus respectivos grupos puntuales no-centro simétricos que pueden presentar piezoelectricidad.
Por ejemplo, en el caso particular de este trabajo donde se van a considerar estructuras monoclínicas con grupo puntual 2, se tiene que el tensor piezoeléctrico toma la siguiente forma:

Para más detalles relacionados con la teoría de la piezoelectricidad, recomendamos revisar [13], [14].
2.2 Método de cálculo para los coeficientes piezoeléctricos
Consideremos un sólido aislado el cual posee N-átomos por celda unitaria, donde Ωo es el volumen de la celda y, adicionalmente, asumamos que en ausencia de campo eléctrico externo el sistema está en equilibrio. En este punto, podemos definir tres tipos de perturbaciones que pueden ser aplicadas al sistema: a) desplazamientos de los átomos alrededor de sus posiciones de equilibrio (um); b) deformación homogénea (nj, con ={1, ···, 6 } en la notación de Voigt [15]); y c) campo eléctrico homogéneo (εa, con a = { x, y, z }). Asociada a cada una de estas perturbaciones, se puede definir una respuesta conjugada, en este caso, la respuesta conjugada a um es la fuerza Fm, a nj el esfuerzo σj y a εa la polarización eléctrica Pa. Adicionalmente, a cada una de estas se le puede asociar las siguientes funciones respuesta, definidas matemáticamente como:

Para determinar las anteriores funciones respuesta, consideremos primero la situación donde no se permiten desplazamientos atómicos internos. Aquí, podemos definir estas funciones respuesta como la segunda derivada de la energía con respecto a las perturbaciones, es decir, respecto a los desplazamientos atómicos, a la tensión, al campo eléctrico aplicado o a las derivadas mixtas de dos de estas perturbaciones. En este caso, el funcional de energía puede ser definida de acuerdo a (9), donde Ecell(o)es la energía del estado base y Ω representa el volumen de la celda deformada. Ahora, vamos a expandir el funcional dado por (9) en una serie de Taylor alrededor de la posición de equilibrio como se observa en (10), en esta ecuación los coeficientes de primer orden Am , Aay Aj son asociados con la fuerza por unidad de volumen (-Fm/Ωo), la polarización eléctrica (-Pa) y con el esfuerzo (σj), respectivamente.
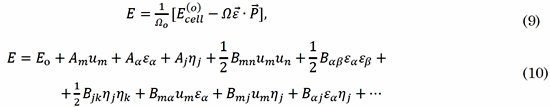
De la misma manera, los coeficientes de segundo orden pueden ser asociados con las funciones respuesta y en nuestro caso particular, nos interesa el tensor piezoeléctrico el cual está asociado con el coeficiente Baj, como se describe en (11), donde no hay desplazamientos atómicos internos cuando un campo eléctrico o tensión homogénea es aplicada al sistema. Sin embargo, la física de las propiedades respuesta de un sistema en presencia de una perturbación, deben tener en cuenta la relajación de las coordenadas iónicas. Para considerar esto, partimos del funcional de la energía, como se muestra en (12), donde vamos a tomar las siguientes condiciones: ∂E/∂un = 0, ∂E/∂εa = 0, ∂E/∂uj = 0 , y a asumir que la configuración de referencia es tal que Am = 0 . Bajo estas condiciones y utilizando la expansión (10), se encuentra que el tensor piezoeléctrico con relajación de las posiciones atómicas es dada por (13), el cual en términos de la polarización eléctrica puede ser escrito como (14), o utilizando relaciones termodinámicas como (15).
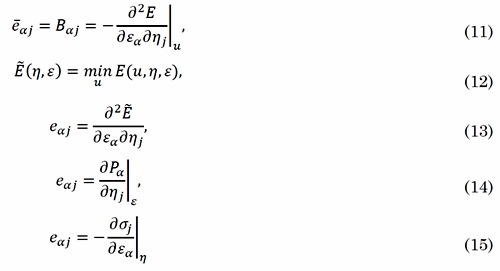
Finalmente, el tensor piezoeléctrico con tensión constante daj definido bajo condiciones de ε y σ controlados es dada por (16), donde los tensores eaj y daj están relacionados a través de la regla (17).


Para más detalles relacionados con este formalismo, recomendamos revisar [8].
2.3 Detalles de la simulación
En este estudio, hemos calculado la geometría del estado base relajando las posiciones de los iones, la forma y el volumen de la celda. Aquí, la energía total, la fuerza entre los iones y las componentes del tensor de esfuerzos fueron calculadas a partir de la teoría de los funcionales de la densidad [16], [17], donde hemos usado para el funcional de intercambio-correlación la aproximación del gradiente generalizado con la parametrización PBEsol [18]. Para resolver las ecuaciones de Kohn-Sham, hemos utilizado el método del proyector de ondas aumentadas [19], tal como está implementado en el código VASP [20], [21]. Para Nb2O5 y Ta2O5, hemos utilizado las siguientes configuraciones atómicas de referencia: 4p6 4d4 5s1 para Nb, 5p6 5d46s1 para Ta and 2s2 2p4 para O, donde únicamente los electrones que aparecen en la configuración electrónica son tratados como electrones de valencia. La energía de corte en la expansión de ondas planas fue de 520 eV. En este caso, la integración en la zona de Brillouin se realizó utilizando una malla 6x6x6 del tipo Monkhorst-Pack y usando una gaussiana de ancho 0.01 eV (las fuerzas sobre los iones fueron convergida a 0.1 meV/Å). Una vez el estado base de cada una de las fases estudiadas aquí fue determinado, realizamos un cálculo usando teoría de perturbaciones para el funcional de la densidad [22], [23], donde solucionamos explícitamente las ecuaciones de Sternheimer para determinar cada una de las componentes del tensor piezoeléctrico.
3. Resultados y Discusión
3.1 Estructura cristalina
En este estudio, analizamos las propiedades piezoeléctricas de las fases Z y P de Nb2O5, y las fases Z y β (modelo Ramprasad) de Ta2O5. En términos de su estructura cristalina, experimentalmente se encontró que la fase Z-Ta2O5 es isoestructural a la fase Z-Nb2O5, ambas representadas por una estructura monoclínica con 14 átomos en la celda convencional formada por cadenas de octaedros Ta(Nb)O6 y poliedros de la forma Ta(Nb)O7. En la Fig. 1 mostramos las estructuras cristalinas asociadas a la fase Z de estos dos compuestos y en la Tabla 2, presentamos su información cristalográfica más relevante. Durante la relajación, la estructura monoclínica se preservó en los dos compuestos.
Por otro lado, la fase β-Ta2O5 es una modificación de la fase L-Ta2O5 a bajas temperaturas sin vacancias de oxígeno, descrita por una estructura ortorrómbica con 14 átomos en la celda convencional. En nuestro cálculo, hemos tomado como referencia la estructura cristalina propuesta por Ramprasad para describir esta fase [7]. En la Fig. 2-(a), mostramos la estructura cristalina de este modelo, donde se tienen cadenas de bipirámides pentagonales TaO7 que comparten los lados con octaedros TaO6. En la Tabla 3, presentamos la información cristalográfica más relevante para esta fase. Es importante mencionar en este punto que en nuestro cálculo durante la relajación, la estructura ortorrómbica original experimentó una pequeña distorsión a una estructura monoclínica simple, donde el ángulo γ se alejó levemente de 90°, tal como fue reportado en un trabajo teórico anterior [4] (en este caso, β- Ta2O5 adquiere una simetría puntual m).
Finalmente, la fase P- Nb2O5 es una fase en el rango de temperatura media, descrita por una estructura tetragonal centrada en el cuerpo con 4 fórmulas estequiométricas por celda unitaria. Para esta fase, la estructura cristalina está compuesta de octaedros Nb2O6 arreglados en la forma que se indica en la Tabla 2-(b). En la Tabla 3, presentamos la información cristalográfica asociada a esta fase. Cabe resaltar que, durante el proceso de relajación de la estructura, la estructura tetragonal original fue preservada.
3.2 Piezoelectricidad
A partir de la geometría de equilibrio y utilizando teoría de perturbaciones para el funcional de la densidad, calculamos la matriz piezoeléctrica para las fases Z y P de Nb2O5, y para las fases Z y β de Ta2O5. Para las fases isoestructurales de estos compuestos (fase Z), encontramos que la matriz piezoeléctrica tiene la misma forma establecida en (3) y están dadas por (18) para Z-Ta2O5 y por (19) Z-Nb2O5.

De (18) y (19), se puede observar que estas fases poseen una muy buena respuesta piezoeléctrica (|eak| ≥ 1) y al ser comparadas indirectamente con ZnO, observamos que algunos coeficientes piezoeléctricos de Z- Ta2O5 y Z- Nb2O5 son el doble o incluso más grandes que los valores para ZnO, como pueden ser evidenciado en la Tabla 4. En esta misma tabla, mostramos una comparación con uno de los mejores piezoeléctricos reportados en la literatura, BaTiO3. De esta comparación, podemos observar que los coeficientes piezoeléctricos de la fase Z en ambos compuestos se encuentran en una región intermedia entre los coeficientes para ZnO y BaTiO3, evidenciando claramente la notable respuesta piezoeléctrica de Ta2O5 y Nb2O5 en su fase Z y perfilándolos como grandes candidatos para aplicaciones en el ámbito tecnológico e industrial donde la piezoelectricidad sea un fenómeno requerido.
Ahora, hablaremos un poco de la respuesta piezoeléctrica encontrada teóricamente para las fases β-Ta2O5 y P-Nb2O5. Para la fase β-Ta2O5, encontramos que nuestro cálculo describe adecuadamente la forma esperada para la matriz piezoeléctrica asociada a la simetría puntual m. Sin embargo, los coeficientes piezoeléctricos calculados son pequeños (del orden 10-³ C/m²), lo cual nos permite concluir que β-Ta2O5 en el modelo de Ramprasad, no presenta respuesta piezoeléctrica. Por otro lado, P-Nb2O5 presenta coeficientes piezoeléctricos grandes, ya sea relajando o sin relajar las posiciones de los iones. Por ejemplo, cuando se relajan las posiciones de los iones, se destacan los siguientes coeficientes piezoeléctricos:
e15 = 2.552 C/m² y e26= -3.099 C/m². Sin embargo, en este caso las matrices piezoeléctricas relajando y sin relajar las posiciones de los iones no presentan la misma estructura y en principio, no respetan la forma impuesta por el grupo puntual 422; evidenciando claramente la inestabilidad dinámica de esta fase, lo cual verifica indirectamente el resultado teórico reportado en [3].
4. Conclusiones
En este trabajo hemos calculado por primera vez, mediante cálculos de primeros principios, la respuesta piezoeléctrica de algunas de las fases de dos interesantes óxidos semiconductores de brecha ancha: Nb2O5 y Ta2O5. Para estos compuestos, encontramos que la fase Z que posee una estructura cristalina monoclínica y simetría puntual 2, presenta coeficientes piezoeléctricos que se encuentran en un rango intermedio entre dos muy buenos materiales piezoeléctricos conocidos: ZnO y BaTiO3; lo cual nos permite declarar que la fase Z en ambos compuestos podría ser utilizada como un interesante piezoeléctrico para diferentes aplicaciones industriales. Adicionalmente, calculamos la respuesta piezoeléctrica de las estructuras β-Ta2O5 (modelo Ramprasad) y P-Nb2O5. La primera, posee coeficientes piezoeléctricos muy pequeños, lo cual permite clasificarla como una fase sin respuesta piezoeléctrica; y la segunda, a pesar de mostrar una respuesta piezoeléctrica alta (incluso mejor que la mostrada por la fase Z en ambos compuestos y comparable en ciertos casos con algunos de los coeficientes piezoeléctricos de BaTiO3), mostró en nuestro cálculo una discrepancia cuando se relajan o permanecen inalteradas las posiciones de los iones respecto a lo esperado para un sistema con simetría puntual 422, evidenciando la inestabilidad dinámica de esta fase.
Referencias
[1] O. F. Lopes, V. R. de Mendonça, F. B. F. Silva, E. C. Paris, and C. Ribeiro, “Niobium Oxides: An Overview of synthesis of Nb2O5 and its application in heterogeneous photocatalysis,” Quim. Nova, vol. 38, p. 1, 2014. [ Links ]
[2] Y. Nakagawa and T. Okada, “Material constants of new piezoelectric Ta2O5 thin films,” J. Appl. Phys., vol. 68, no. 2, pp. 556-559, Jul. 1990. [ Links ]
[3] C. Valencia-Balvín, S. Pérez-Walton, G. M. Dalpian, and J. M. Osorio-Guillén, “First-principles equation of state and phase stability of niobium pentoxide,” Comput. Mater. Sci., vol. 81, pp. 133-140, Jan. 2014. [ Links ]
[4] S. Pérez-Walton, C. Valencia-Balvín, A. C. M. Padilha, G. M. Dalpian, and J. M. Osorio-Guillén, “A search for the ground state structure and the phase stability of tantalum pentoxide,” J. Phys. Condens. Matter, vol. 28, no. 3, p. 35801, Jan. 2016. [ Links ]
[5] I. P. Zibrov, V. P. Filonenko, P.-E. Werner, B.-O. Marinder, and M. Sundberg, “A New High-Pressure Modification of Nb2O5,” J. Solid State Chem., vol. 141, no. 1, pp. 205-211, Nov. 1998. [ Links ]
[6] I. P. Zibrov, V. P. Filonenko, M. Sundberg, and P.-E. Werner, “Structures and phase transitions of B-Ta2O5 and Z-Ta2O5: two high-pressure forms of Ta2O5,” Acta Crystallogr. Sect. B Struct. Sci., vol. 56, no. 4, pp. 659-665, Aug. 2000. [ Links ]
[7] R. Ramprasad, “First principles study of oxygen vacancy defects in tantalum pentoxide,” J. Appl. Phys., vol. 94, no. 9, pp. 5609-5612, Nov. 2003. [ Links ]
[8] X. Wu, D. Vanderbilt, and D. R. Hamann, “Systematic treatment of displacements, strains, and electric fields in density-functional perturbation theory,” Phys. Rev. B, vol. 72, no. 3, p. 35105, Jul. 2005. [ Links ]
[9] M. Audier, B. Chenevier, H. Roussel, L. Vincent, A. Peña, and A. Lintanf Salaün, “A very promising piezoelectric property of Ta2O5 thin films. II: Birefringence and piezoelectricity,” J. Solid State Chem., vol. 184, no. 8, pp. 2033-2040, Aug. 2011. [ Links ]
[10] M. Audier, B. Chenevier, H. Roussel, L. Vincent, A. Peña, and A. Lintanf Salaün, “A very promising piezoelectric property of Ta2O5 thin films. I: Monoclinic-trigonal phase transition,” J. Solid State Chem., vol. 184, no. 8, pp. 2023-2032, Aug. 2011. [ Links ]
[11] C. Kane and J. Moore, “Topological insulators,” Phys. World, vol. 24, no. 2, pp. 32-36, Feb. 2011. [ Links ]
[12] D. B. C Goringe and E. Hernandez, “Tight-binding modelling of materials,” Rep. Prog. Phys., vol. 60, pp. 1447-1512, 1997. [ Links ]
[13] A. L. Kholkin, N. A. Pertsev, and A. V Goltsev, “Piezoelectricity and Crystal Symmetry,” in Piezoelectric and Acoustic Materials for Transducer Applications, Boston, MA: Springer US, 2008, pp. 17-38. [ Links ]
[14] R. E. Newnham, Properties of materials. Oxford University Press New York, 2005. [ Links ]
[15] W. Voigt, Lehrbuch der Kristallphysik. Wiesbaden: Vieweg+Teubner Verlag, 1966. [ Links ]
[16] J. P. Perdew, A. Ruzsinszky, L. A. Constantin, J. Sun, and G. I. Csonka, “Some Fundamental Issues in Ground-State Density Functional Theory: A Guide for the Perplexed,” J. Chem. Theory Comput., vol. 5, no. 4, pp. 902-908, Apr. 2009. [ Links ]
[17] A. M.-A. W Espinosa-García and J. M. Osorio-Guillén, “Electronic properties of the sulvanite compounds: Cu3TMS4 (TM= V, Nb, Ta),” Rev. Colomb. Física, vol. 40, pp. 36-39, 2008. [ Links ]
[18] J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou, and K. Burke, “Restoring the Density-Gradient Expansion for Exchange in Solids and Surfaces,” Phys. Rev. Lett., vol. 100, no. 13, p. 136406, Apr. 2008. [ Links ]
[19] P. E. Blöchl, “Projector augmented-wave method,” Phys. Rev. B, vol. 50, no. 24, pp. 17953-17979, Dec. 1994. [ Links ]
[20] G. Kresse and D. Joubert, “From ultrasoft pseudopotentials to the projector augmented-wave method,” Phys. Rev. B, vol. 59, no. 3, pp. 1758-1775, Jan. 1999. [ Links ]
[21] G. Kresse and J. Furthmüller, “Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set,” Phys. Rev. B, vol. 54, no. 16, pp. 11169-11186, Oct. 1996. [ Links ]
[22] P. Giannozzi and S. Baroni, “Density-Functional Perturbation Theory,” in Handbook of Materials Modeling, Dordrecht: Springer Netherlands, 2005, pp. 195-214. [ Links ]
[23] C. M. R. y Jorge M Osorio-Guillén, “Estudio teórico de las propiedades elásticas de los minerales Cu3TMSe4 (TM = V, Nb, Ta) por medio de cálculos atomísticos de primeros-principios,” Ing. Cienc., vol. 7, no. 1, pp. 1644-1650, 2011 [ Links ]




















