1. INTRODUCCIÓN
La comunidad científica ha trabajado intensamente durante décadas tratando de entender y formalizar la incertidumbre. La mayor incertidumbre en un problema es lo menos preciso o correcto que se pueda estar del entendimiento de este, es así que muchos analistas están de acuerdo en que se debería entender y evaluar la incertidumbre que existe en la solución de problemas, o hacer predicciones, tratando de buscar un punto de equilibrio entre la incertidumbre y la precisión que se busca [1]. La incertidumbre de una medición se define como un parámetro no negativo que caracteriza la dispersión de los valores atribuidos a un mensurando, a partir de la información utilizada, y dependiendo de cómo esta dispersión es caracterizada, incluye componentes de efectos sistemáticos, tales como los asociados a correcciones y valores asignados a patrones [2].
En cuanto al medio ambiente, las implicaciones de la incertidumbre son particularmente relevantes en la evaluación de las posibles opciones de regulación, como es el seguimiento y control de los niveles de calidad del aire [3]. Actualmente, con el incremento de la aplicación de la metrología en las mediciones ambientales, se han explorado diferentes metodologías para la estimación de la incertidumbre, entre las cuales se incluye la aplicación de la Guía para la Expresión de la Incertidumbre de Medida (GUM), la cual se ha derivado de una metodología no estocástica [4]. Esta guía ha sido ampliamente aceptada dentro de la comunidad científica desde su primera versión de 1993 y para el 2017 permanece vigente la versión del año 2008 [5]. La GUM cuenta, además, con dos complementos para su aplicación. El primero es una introducción con documentos relacionados [6]; y el segundo es un suplemento que permite trabajar con modelos multivariados y cualquier número de variables de salida [7]. La complejidad de los modelos matemáticos requerida para estimar la incertidumbre asociada con los inventarios de emisiones para fuentes fijas, como también el seguimiento dinámico a esas emisiones, ha limitado la aplicación de la GUM, si bien, son frecuentes aplicaciones de esta [8], [9], [10], es más común encontrar trabajos usando otros métodos como Monte Carlo, Bootstrap, Intervalo Generalizado, Conjuntos Difusos, entre otros [3], [11], [12], [13], [14], [15], [16]. Las emisiones contaminantes de las fuentes fijas pueden ser monitoreadas de forma continua [17] o mediante los métodos definidos por la Agencia de Protección Ambiental de los Estados Unidos (US EPA) [18], estos últimos adoptados en Colombia mediante la Resolución 0935 de 2011 por el Instituto de Hidrología, Meteorología y Estudios Ambientales [19]. Ambas formas de monitoreo requieren de la estimación de la incertidumbre asociada al proceso de medición con el fin de garantizar la trazabilidad y validez de los datos generados, para así poder usarlos en la verificación de cumplimientos legales y elaboración de inventarios de emisiones. Dentro de la literatura revisada sobre la determinación de la incertidumbre asociada a las emisiones en fuentes fijas, resalta el trabajo desarrollado por [20], donde la guía GUM es aplicada para la estimación de la incertidumbre asociada al monitoreo de Óxidos de Nitrógeno (NOX), usando el método US EPA 7 [20].
En este artículo, se realiza una revisión del estado del arte en la evaluación de la incertidumbre de medición, se exploran los diferentes métodos y metodologías disponibles para su estimación, y el grado de aplicación de las mismas al campo de las mediciones de las emisiones de fuentes fijas, para lo cual se inicia con una revisión sobre las metodologías disponibles para la estimación de la incertidumbre y se termina con los hallazgos de los estudios realizados aplicados al área de interés del estudio. Además, la revisión destaca las fortalezas, debilidades, grado de difusión y aplicación de cada una de las metodologías que estiman la incertidumbre.
2. ESTIMACIÓN DE LA INCERTIDUMBRE: METODOLOGÍAS Y APLICACIONES
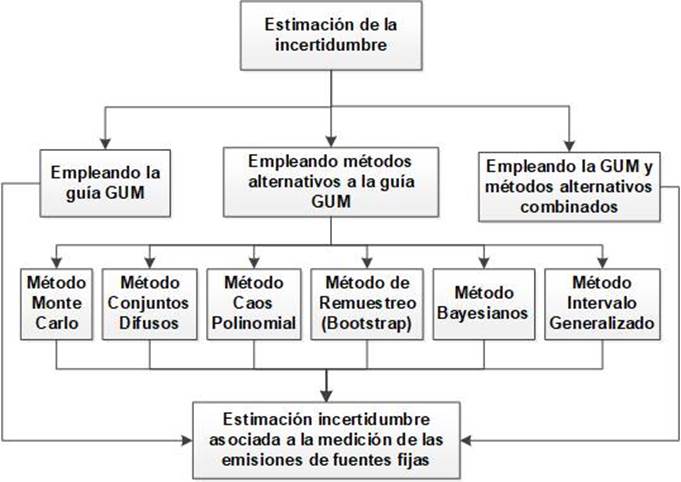
En la Fig. 1, se muestra un esquema general de los métodos para la estimación de la incertidumbre, y el uso de estos en la cuantificación de la incertidumbre asociada a la determinación de las emisiones desde fuentes fijas.
Dentro de la variabilidad de propuestas para la estimación de la incertidumbre, se encuentran herramientas como la GUM [5], Conjuntos Difusos [12], Caos Polinomial [13], Remuestreo (Bootstrap) [14], Inferencia Bayesiana [15], Intervalo Generalizado [16] y Monte Carlo (MCM) [21]. La combinación de la GUM con otros métodos de estimación, se ha empleado principalmente en aquellos casos donde los modelos matemáticos son muy complejos y la aplicación de la guía GUM resulta difícil de implementar, debido a la imposibilidad de realizar una identificación exhaustiva de todas las fuentes de incertidumbre y sus respectivas distribuciones estadísticas asociadas, lo que conduce a que se deban realizar simplificaciones del modelo de propagación de la incertidumbre [22]. Una ventaja del uso de ambas metodologías de forma simultánea, es que permite validar las simplificaciones realizadas en el proceso de estimación de la incertidumbre al aplicar la guía GUM.
2.1 Estimación de la incertidumbre aplicando la guía GUM y documentos relacionados
La evaluación de la incertidumbre puede hacerse por métodos como el propuesto en los documentos desarrollados por el Joint Committee for Guides in Metrology (JCGM), entre los documentos desarrollados está la guía GUM [5], la cual está compuesta por un documento introductorio y otros reportes relacionados [6], además del suplemento 2, el cual permite trabajar con modelos multivariados en relación con cualquier número de variables de salida o múltiples mesurandos [7]. La guía GUM desde su primera versión publicada en 1993, estableció una serie de recomendaciones con gran acogida por la comunidad científica, lo que llevó a que se presentaran numerosas aplicaciones de esta en diferentes campos del conocimiento, entre los que se incluye: implementación de un procedimiento para la incertidumbre combinada en mediciones de espectrometría gamma [23], mediciones analíticas a través el desarrollo de la guía para la cuantificación de la incertidumbre [24], evaluación y discusión de la estimación de la incertidumbre en análisis farmacéuticos [25], entre otros.
En la primera línea de la Fig. 2, se presentan las guías propuestas por el JCGM para la aplicación de la guía GUM, así como un recuento de algunas publicaciones que han usado esta guía para estimar la incertidumbre de medición, mientras en la segunda y tercera línea, se hace mención de aquellos trabajos que buscan cubrir aspectos necesarios para la estimación de la incertidumbre y que la GUM no contempla o incluye para su implementación.

Fuente: autores.
Fig. 2 Aplicación de la GUM y documentos relacionados en la estimación de la incertidumbre.
Cuando la estimación de la incertidumbre se realiza mediante el uso de distribuciones de probabilidad, se identifican dentro de la literatura diferentes trabajos que abordan vacíos que posee la GUM para su implementación, entre los cuales están: evaluación de la incertidumbre en mediciones, problemas y herramientas [4]; evaluación de la incertidumbre para múltiples mediciones usando GUM [26]; evaluación de la incertidumbre para múltiples mediciones usando GUM, parte II [27]; exactitud de mediciones simples, las cuales no son mencionadas por la GUM [28]; aplicación para el chequeo de consistencia en la evaluación de la incertidumbre en mediciones de múltiples réplicas [29]; de la GUM a métodos alternativos para la evaluación de la incertidumbre de medición [30]; evaluación de la incertidumbre para múltiples mediciones por GUM, parte III, usando coeficientes de correlación [31].
De otra parte, [32], discuten el problema de la cuantificación del error sistemático sobre la medición de la incertidumbre total, eludiendo los conceptos de grados de libertad y probabilidad subjetiva que hacen parte de la razón de ser de la GUM, aplicados al caso cuando la función de medición es fuertemente no-lineal y el uso de la aproximación lineal puede ser inadecuada, donde los términos de orden superior de la serie de Taylor no pueden ser despreciados, para lo cual se propone el uso de expresiones generalizadas para aquellos términos de segundo y tercer orden en la evaluación de la incertidumbre estándar [33], mientras en el trabajo desarrollado por [34], se realiza una revisión de las debilidades de la guía GUM cuando se efectúan mediciones con resultados cercanos a cero.
Por otro lado, se encuentran publicaciones como las mostradas en la cuarta línea de la Fig. 2, encaminadas a extender la implementación de la GUM, tal es el caso del trabajo propuesto por [35], en el cual se estima la incertidumbre de medición mediante el desarrollo de una aplicación que emplea el software comercial (Maple) y que permite trabajar con funciones simbólicas, caso similar al mostrado por [36], donde se pone en evidencia las ventajas del cálculo simbólico frente al numérico para la estimación de las derivadas parciales, cuando se emplean diferentes paquetes comerciales.
Por otro lado, trabajos como el de Zang [37] buscan ayudar a la interpretación de la GUM y resumen las terminologías de probabilidad pertinentes para la cuantificación de la incertidumbre en ingeniería, mientras [38] presentan ideas y observaciones sobre el uso del frecuentismo y la aplicación de la inferencia bayesiana en la estimación de la incertidumbre, en términos de méritos y fallas de la aplicación bayesiana comparada con la frecuentista. El trabajo desarrollado por [39] describe la manera de obtener mediciones confiables, usando la expresión de trazabilidad metrológica junto con la medición de incertidumbre. Las deficiencias de la metodología GUM, son expuestas y presentadas bajo el término de incertidumbre oscura por [40], la cual se refiere a aquella incertidumbre que aparece como una dispersión grande e inesperada de los valores, y examina la evidencia de su ocurrencia al comparar los resultados obtenidos por la GUM frente a los arrojados por la reproducibilidad estimada a partir de las comparaciones entre los diferentes laboratorios. Los resultados muestran una tendencia general en la cual los valores de incertidumbre estándar estimados empleando la guía GUM son sustancialmente inferiores a la desviación estándar de reproducibilidad, lo que evidencia problemas de implementación de la GUM al no incluir todas las fuentes de incertidumbre en el modelo de propagación.
2.2 Métodos alternativos a la GUM para la estimación de la incertidumbre
La metodología basada en la GUM por derivadas parciales presenta varias limitaciones, en primer lugar, implica el cálculo de derivadas de primer orden para cada componente de la magnitud de salida, requiriéndose un considerable procesamiento matemático especializado, que puede llegar a ser exhaustivo si el modelo matemático es complejo; y en segundo lugar, esta no tiene la posibilidad de hacer predicciones exactas sobre la distribución de probabilidad de la magnitud de salida, si las magnitudes de entrada no tienen distribución normal [41], y es bien conocido que el conocimiento de la distribución de probabilidad es esencial para determinar el intervalo de cobertura.
La Fig. 3 muestra el diagrama conceptual sobre la revisión de diferentes trabajos basados en otros métodos para la estimación de la incertidumbre. Entre los métodos revisados el de mayor difusión y aceptación es el Método Monte Carlo, el cual realiza un muestreo aleatorio de las distribuciones de probabilidad de las magnitudes de entrada; por lo tanto, no requiere calcular derivadas de primer orden, ni la función de densidad de probabilidad de la magnitud de salida. En el suplemento 1 del JCGM para estimación de la incertidumbre usando el MCM, se dan condiciones específicas sobre cuándo es aplicable el método GUM a sistemas lineales y no lineales y en qué casos es preferible el uso de una herramienta como MCM [42].

Fuente: autores.
Fig. 3 Aplicación de métodos alternativos a la GUM en la estimación de la incertidumbre.
El MCM se utilizó para la estimación de la incertidumbre por [42], quienes describen la situación actual de la evaluación de la incertidumbre en el contexto de las normas internacionales, y se recomienda una aplicación usando Monte Carlo para la evaluación de la incertidumbre de medición basada en la propagación de distribuciones. El método Monte Carlo ha sido también empleado para estimar la incertidumbre en modelos fuertemente no lineales [43], y ha demostrado ser una herramienta efectiva y versátil para la determinación de funciones de distribuciones de probabilidad (pdf) para mesurandos [44]. Adicionalmente, se han desarrollado algoritmos que permiten al usuario elegir la distribución de salida preferida para el mesurando [45], más que la asignada implícitamente en el suplemento 1 de la GUM, esto unido a investigaciones que buscan mejorar la eficiencia de muestreo y convergencia del método Monte Carlo [46], con el fin de reducir el gasto computacional tanto como sea posible.
Para la estimación de la incertidumbre existen otros métodos, como es Caos Polinomial, el cual es más apropiado para modelos a gran escala, donde el método Monte Carlo converge lentamente [13], o en modelos de alta complejidad como ocurre con las ratas de reacción al interior de un reactor [47]. El método Bootstrap ha sido utilizado para aquellos casos donde el método Monte Carlo no puede ser aplicado directamente para la caracterización de la incertidumbre, como es el caso de ensayos donde no se puede medir directamente la magnitud de interés [14], asimismo este método se ha empleado para la estimación de la incertidumbre en la inferencia de los estimativos de las reservas de petróleo y gas [48].
Otro método es la Inferencia Bayesiana, por medio de la cual se ha demostrado [15] que hay maneras alternativas de aplicar el teorema de Bayes y que estas formulaciones alternativas producen los mismos resultados. El método bayesiano comparado con el método clásico (GUM), es más corto y no requiere conocer todas las etapas individuales en los cuales un proceso puede ser descompuesto (ejemplo: aplicaciones de métodos analíticos o bio-analíticos), ya que es tomado como un todo [49]. El método bayesiano también ha mostrado sus bondades en la cuantificación de la incertidumbre asociada a la selección del mejor modelo [50], lo cual puede ser problemático debido a la posible subestimación de la variabilidad de las predicciones. Por último, se referencian otros dos métodos que han sido empleados en la estimación de la incertidumbre: los Conjuntos Difusos [12] y el Intervalo Generalizado [16]. De todos los métodos alternativos a la GUM, el que cuenta con mayor difusión y aplicabilidad es Monte Carlo, al punto que el JCGM emitió en 2008 una guía con el fin de ayudar en su implementación [21]. En general, se encuentra que muchos de los esfuerzos investigativos sobre el uso de métodos alternativos a la GUM para estimar la incertidumbre, se centran en la obtención de un método estadístico estable que permita una muy buena determinación de la incertidumbre de los procesos de medición, que paralelamente disminuya el porcentaje de duda en los cálculos matemáticos y permita crear un modelo que se acerque al proceso de medición real, tomando todas las fuentes involucradas en el proceso.
2.3 Estimación de la incertidumbre empleando métodos combinados
Por otro lado, se encuentran los estudios en los cuales se ha utilizado la combinación de diferentes métodos de estimación, como los que se muestran en la Fig. 4.

Fuente: autores.
Fig. 4 Aplicación de la GUM y métodos alternativos combinados a la estimación de la incertidumbre.
La aplicación de métodos híbridos a la estimación de la incertidumbre es amplia y comprende diferentes campos del conocimiento, entre los que se incluyen trabajos donde se aplica MCM y la guía GUM como son: estimación de la incertidumbre en pruebas de compatibilidad electromagnética [22], análisis de cadmio por GFAAS [51], medición del poder calórico de combustión de un combustible usando una bomba calorimétrica [52], y mediciones de resistencia y potencia eléctrica [53], asimismo, se encuentran trabajos como el desarrollado por Torres [54], donde se usan ambas metodologías de estimación en la cuantificación de la incertidumbre asociada a la determinación de la concentración de sólidos totales, mientras [55], describe las propiedades y limitaciones de la estructura para estimar la incertidumbre de la GUM y el método Monte Carlo, empleando un modelo de razones. De forma similar, una aplicación para la estimación de la incertidumbre basada en la teoría del Caos Polinomial es propuesta por [56] y se compara con el método tradicional basado en la guía GUM. Por último, [1] desarrollan un panorama de la evolución de la estimación de la incertidumbre, tanto desde el punto de vista estocástico como no estocástico.
2.4 Métodos empleados a la estimación de la incertidumbre en fuentes fijas
Una vez completada la revisión de las metodologías para estimación de la incertidumbre y sus aplicaciones en diferentes campos, la revisión se centra en identificar aquellos trabajos donde se han empleado diferentes herramientas, tanto de carácter estocástico como no estocástico, en la estimación de la incertidumbre asociada a las emisiones de fuentes fijas. Dentro de estos trabajos se resaltan los que se presentan en las líneas primera y segunda de la Fig. 5, y que se pueden clasificar en dos partes, la primera comprende los trabajos identificados con las siglas INCESPTEMP e INCTEMP, que se orientan a estimar la variación espacio temporal de las fuentes y la incertidumbre asociada, dentro de esta categoría se encuentra una amplia cantidad de estudios en la literatura, entre los que se incluyen los realizados para la elaboración de los inventarios de gases de efecto invernadero (GHG) [8], [9], [11], [57], [58], [59], así como trabajos donde se estima la variación temporal mediante la recolección de datos de mediciones continuas, los cuales se pueden usar para cuantificar la incertidumbre asociada mediante métodos como Monte Carlo, Bootstrap y Conjuntos Difusos [3], [60]. Por otra parte, la segunda corresponde a los trabajos identificados con la sigla INCESTMED, usados para estimar la incertidumbre asociada a la medición instrumental de la emisión desde fuentes fijas, empleando los métodos definidos en el Código Federal de Regulaciones (CFR), título 40 parte 60 Apéndices A1 a A8 [18], el cual incluye métodos para la determinación de Material Particulado (MP), Óxidos de Nitrógeno (NOx), Dióxido de Azufre (SO2) y Neblinas Ácidas (H2SO4), entre otros. Al respecto son escasas las publicaciones en la literatura, de tal manera que esta revisión solo logró identificar el trabajo desarrollado por [20], donde se aplica la GUM para la estimación de la incertidumbre asociada a la medición de las emisiones de NOx, cuando la muestra es colectada de acuerdo con lo descrito en el método EPA 7 “Determinación de emisiones de óxidos de nitrógeno de fuentes fijas”.
3. CONCLUSIONES Y RECOMENDACIONES
Son pocas las publicaciones en la literatura referidas a metodologías específicas que permitan estimar la incertidumbre asociada al procedimiento instrumental empleado para la determinación de las emisiones de fuentes fijas, cuando se aplican los métodos 1 al 8 propuestos por la Agencia de Protección Ambiental de los Estados Unidos (US EPA). Esta revisión encontró que, entre los pocos trabajos en esta área, se encuentra el reportado en [20], el cual solo se limita a la estimación de la incertidumbre para el método EPA 7 mediante la aplicación de la guía GUM, sin cubrir los métodos restantes y la posibilidad de implementar métodos de estimación alternativos.
La revisión permitió, además, identificar que la aplicación de la metodología de estimación propuesta en la guía GUM, a la estimación de la incertidumbre asociada a la medición de fuentes fijas, requiere superar los siguientes inconvenientes: 1) Incremento de complejidad cuando el método de medición comprende muchas etapas y cada una contribuye a la incertidumbre del resultado final; 2) Conocer con exactitud la distribución estadística asociada a cada fuente, con el fin de poder reducirla e ingresarla al modelo de propagación en el que se basa la GUM; 3) Suponer un comportamiento lineal de la función de medición, aunque hay casos en los cuales esta es fuertemente no-lineal y el uso de la aproximación lineal puede ser inadecuada, dado que los términos de orden superior de la serie de Taylor no pueden ser despreciados; 4) Calcular derivadas de primer orden de cada componente de la magnitud de salida, lo cual demanda buen entendimiento y procesamiento matemático y puede ser agotador si el modelo matemático es complejo; 5) Predecir la distribución de probabilidad de la magnitud de salida con precisión, cuando las magnitudes de entrada no poseen distribución normal; y 6) La imposibilidad de ingresar al modelo todas las fuentes de incertidumbre, ya sea porque se desconoce su presencia, o no se cuenta con un estimativo de su influencia.
De otra parte, se encuentran los métodos alternativos que a diferencia de la metodología basada en la GUM no poseen todas las limitaciones anteriores, pero en cambio presentan inconvenientes, como: 1) Incremento de los costos computacionales, que puede convertirse en un factor limitante para su implementación; 2) Algunos métodos estocásticos, como Monte Carlo requieren de la selección apropiada de la distribución estadística para los parámetros del modelo, lo cual puede ser un inconveniente debido a la falta de compresión subyacente de los fenómenos físicos; y 3) El grado de conocimiento requerido para la selección e implementación del método más apropiado a usarse, exige un alto grado de experticia, cuando se compara con el requerido para el empleo de la guía GUM.
La aplicación en simultáneo de ambas metodologías, GUM y métodos alternativos, para la estimación de la incertidumbre, ha permitido una validación de los resultados obtenidos cuando los modelos matemáticos que se trabajan son complejos y la identificación de todas las fuentes de incertidumbre puede convertirse en un procedimiento extenuante, de forma que la aplicación de la metodología basada en la guía GUM tiende a subestimar el valor de la incertidumbre, y el uso en simultáneo con otro método permite su validación.
La necesidad de cuantificar la incertidumbre radica en el papel que juega en las mediciones y en su importancia como herramienta para dar solución al problema que se presenta cuando se requiere la toma de decisiones que involucran límites de carácter regulatorio, o de conformidad, como es el caso de las mediciones de las emisiones de fuentes fijas. Es por esto, que se requieren nuevos estudios para el desarrollo de una metodología conjunta que implemente métodos estocásticos y no estocásticos, para la determinación de la incertidumbre asociada a la determinación de las emisiones de este tipo de evaluaciones, con el fin de alcanzar un mejoramiento importante en el proceso de medición de fuentes fijas.