1. INTRODUCCIÓN

Los filtros activos de potencia o Active Power Filters (APF) son utilizados para la mitigación de armónicos producidos por cargas no lineales en los sistemas eléctricos de distribución. Dichos armónicos generan efectos nocivos, tanto en la red de distribución como en las cargas eléctricas de los usuarios que se conectan a ella ^[1]. Los APF se clasifican como serie, paralelo y mixtos, dependiendo del tipo de conexión con respecto a la carga. El APF en conexión paralelo o Shunt Active Power Filter (SAPF) es la conexión que se utliza en este trabajo. Su funcionamiento es similar al de una fuente de corriente controlada que inyecta componentes armónicas en contrafase a las que absorbe la carga no lineal, para anular su efecto en el punto de conexión de la carga con la red o Point of Common Coupling (PCC). De esta forma, otras cargas conectadas en el PCC no evidencian la presencia de armónicos y operan en condiciones normales de alimentación sinusoidal ^[2].

Un APF está constituido por cinco componentes: un elemento almacenador de energía, un elemento de acople con la red de alimentación, un convertidor de Corriente Continua (CC) a Corriente Alterna (CA) conocido como inversor, un controlador y circuitos de acondicionamiento de señal. En un SAPF se utiliza un condensador en el lado de CC del inversor como elemento de almacenamiento de energía en forma de tensión continua. Debido a esta característica, el inversor se denomina de fuente de tensión o Voltaje Source Inverter (VSI). El elemento de acople por fase del SAPF con la red de alimentación es una inductancia, que fija la rapidez de variación de las corrientes de compensación. El controlador es el encargado de determinar las señales de control que gobiernan los estados de los semiconductores del inversor. Requiere de mediciones de algunas variables del sistema, como tensiones y corrientes, por lo que su funcionamiento depende de sensores y circuitos de acondicionamiento de señal ^[3].

En la operación de los SAPF se realizan tres acciones en el controlador. Primero, se obtienen las corrientes de referencia mediante la ejecución de un algoritmo para el cálculo de la compensación de armónicos ^[4]. Generalmente, se realizan mediciones de tensiones y corrientes, se evalúa el contenido armónico y se determinan sus armónicos en contrafase para ser inyectadas en el PCC. Segundo, se mantiene en un valor de referencia la tensión en el condensador del lado de CC del inversor, absorbiendo de la red de alimentación la energía eléctrica y suministrando potencia en el PCC para realizar la compensación de armónicos. Tercero, una técnica de modulación de ancho de pulso o Pulse Width Modulated (PWM) se encarga de sintetizar las corrientes de compensación por medio del inversor, a través de la conmutación de los semiconductores. En Fig. 1, se muestran las partes del controlador y su integración, en la operación de los SAPF.

Fuente: autores.

Fig. 1 Esquema general de un SAPF incluyendo el sistema de control. 

En general, el control de corriente del SAPF por PWM requiere de la señal obtenida con el algoritmo para el cálculo de compensación de armónicos, para generar una señal en forma de pulsos modulados en amplitud que conmutan los estados de los semiconductores del inversor. En ^[5] se plantean diferentes técnicas PWM agrupadas en las siguientes categorías: modulación basada en portadora, modulación por banda fija de histéresis y modulación por banda adaptativa de histéresis. La modulación basada en portadora se clasifica como escalar o vectorial, y es muy común en accionamientos eléctricos e inversores de potencia por su alto desempeño y alta eficiencia ^[6]. La técnica por banda fija de histéresis es la más común en los SAPF debido a su simplicidad y rápida respuesta ^[7]. También se utiliza en SAPF híbridos como se describe en ^[8].

La modulación por banda adaptativa de histéresis presenta ventajas comparativas respecto a banda fija ^[9], razón por la cual se estudia ampliamente en la literatura. En la modulación por banda adaptativa, el valor del ancho de la banda para establecer la conmutación de los semiconductores del inversor, cambia según las características del circuito y los objetivos de control orientados principalmente a la optimización de la frecuencia de conmutación y la compensación de armónicos. En ^[10] el ancho de banda se define según la frecuencia, el valor de la fuente de tensión de CC y las pendientes de la corriente de referencia. En ^[11], el valor de la banda cambia de acuerdo con la variación de las corrientes de referencia, optimizando la frecuencia de conmutación. En ^[12], la banda de histéresis cambia con el objetivo de reducir la distorsión armónica total o Total Harmonic Distortion (THD) a un valor mínimo. Mientras que en ^[13] este valor se determina de tal forma que disminuye el rizado de la señal de compensación inyectada en el PCC. Otras variantes de la modulación por banda adaptativa de histéresis son optimizar el desempeño del elemento almacenador de energía del filtro activo ^[9] y aplicaciones basadas en lógica difusa ^[14]. También, es factible mejorar la respuesta dinámica de la modulación por banda adaptativa utilizando la modulación vectorial, como se describe en ^[15], donde se presentan diferentes implementaciones.

El aporte de este trabajo de investigación es realizar un análisis comparativo de las diferentes técnicas PWM utilizadas en SAPF. Trabajos previos muestran comparaciones entre algunas técnicas como banda fija de histéresis y modulación vectorial ^[16], banda fija y banda adaptativa ^[17], pero no se encuentra en la literatura un análisis más amplio que relacione las técnicas de modulación vectorial, banda fija y banda variable de histéresis.

Este trabajo está organizado de la siguiente manera: en la metodología se presenta la estructura de un SAPF, se describe el algoritmo de compensación de armónicos utilizado y las técnicas PWM implementadas. Además, se muestra el procedimiento para ajustar la ganancia del controlador de la tensión de CC del inversor. En los resultados se muestra un análisis comparativo de los resultados obtenidos con las técnicas PWM, considerando la frecuencia de conmutación, las pérdidas por conmutación y la distorsión armónica de las corrientes en la red de alimentación. Las conclusiones de la investigación se presentan al final del artículo.

2. MÉTODOS

2.1 Estructura APF

El SAPF utilizado en este trabajo se muestra en Fig. 2. El sistema consiste en un inversor de tres ramas y un condensador en el lado de CC, debido a su bajo costo en comparación con otras topologías, para sistemas de baja tensión ^[18]. El SAPF se conecta a la red por medio de la inductancia de acoplamiento L, que en ocasiones representa la inductancia de dispersión de un transformador con relación 1:1. En aras de la claridad, en Fig. 2 se omite las cargas (lineales y no lineales), que deben estar conectadas en los terminales abc de la red de alimentación.

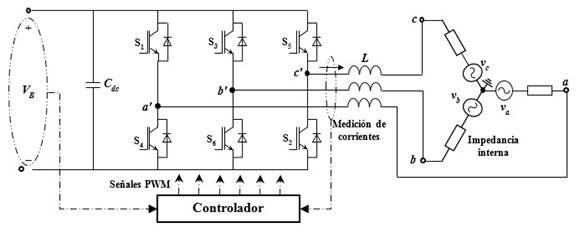
Fuente: autores.

Fig. 2 Inversor trifásico de tres ramas y dos niveles conectado a una fuente trifásica. 

A continuación se describe el algoritmo utilizado para obtener las corrientes de compensación y las técnicas utilizadas para generar las señales de mando o PWM de los interruptores del inversor.

2.2 Algoritmo para obtener las corrientes de referencia

En este trabajo se utiliza el algoritmo basado en la teoría pq, propuesta en ^[19]. El algoritmo se basa en descomponer la potencia activa que absorben las cargas no lineales de la red en dos componentes (una constante y otra alterna), como se indica en (1).

La componente constante pcc se genera por las componentes de secuencia positiva de las tensiones y corrientes de la carga, mientras que la componente alterna pca se debe a los armónicos y a las componentes de secuencia negativa presentes en las tensiones y corrientes de la carga.

Para hallar las corrientes de referencia, se establece que el SAPF le suministre a la carga la componente p _ca de la potencia activa y toda la potencia reactiva q que absorbe la carga, con lo que se obtiene en la red de alimentación un suministro de potencia constante a la carga p _cc, como si está se comportara como una carga lineal, con corrientes sinusoidales circulando en la red de alimentación.

Para separar las componentes de potencia p _cc y p _ca, se utiliza la matriz que se indica en (2), también conocida como la transformada de Clarke. Mediante esta matriz de transformación las tensiones y las corrientes trifásicas de la carga se refieren al marco de referencia α-β-0.

donde, representa una tensión o una señal de corriente. La potencia activa p y reactiva q se calculan en el sistema de referencia α-β-0 mediante las ecuaciones (3) y (4).

Luego, a través de un filtro de señal pasa alto, se extrae la componente alterna de p, para que sea suministrada por el SAPF. Durante la operación, el SAPF absorbe potencia activa de la red denominada como pAPF , para mantener constante la tensión en el lado de CC del inversor. Además, el filtro suministra la potencia activa y reactiva necesaria para realizar la compensacion de armónicos en el PCC. Los detalles del cálculo de está potencia se explican en la siguiente sección.

El primer paso para el cálculo de las corrientes de compensación es hallar p y q aplicando (3) y (4) y luego, se evalúa la ecuación (5). En esta ecuación, las corrientes se expresan en función de las tensiones y se tiene en cuenta que la potencia de compensación es pca - pAPF. Aplicando (6), se obtiene la corriente de compensación en el eje 0, es la corriente obtenida con la transformación de Clarke en el eje 0.

Finalmente, con la transformada inversa de Clarke se calculan las corrientes de referencia trifásicas iabc* en coordenadas abc. El algoritmo se describe gráficamente a través del diagrama de bloques que se muestra en la Fig. 3.

Fuente: autores.

Fig. 3 Diagramas de bloques del algoritmo para calcular las corrientes de referencia, utilizando la teoría pq. 

2.3 Control de la tensión CC del inversor

La energía almacenada en un condensador está dada por (7).

donde Vcc es la tensión del condensador Cdc. La variación de la energía en el condensador respecto a su valor de referencia, está dado por (8).

donde Vdc,ref es la tensión de referencia en el condensador. Suponiendo que VB,ref + VB ≈ 2VB,ref [²⁰], se obtiene (9) para la variación de energía del condensador.

La dinámica en la energía del condensador depende del intercambio de energía que el elemento realiza con la red de alimentación. Este comportamiento se caracteriza por tensiones y corrientes periódicos cada T segundos. La variación de energía se puede expresar en términos de variación de potencia como se indica en (10).

Reemplazando (9) en (10) se obtiene (11), que muestra la potencia que requiere el condensador en cada ciclo de red para mantener su energía en un valor constante.

El término que múltiplica al error de voltaje , es la constante de proporcionalidad del controlador del inversor, y sus unidades son Amperios. Por lo tanto, la constante del controlador de tensión está dada por (12).

2.5 Banda fija de histéresis

Para simplificar, se considera la fase a del sistema de potencia (sucede lo mismo para las demás fases). La corriente en la fase a, inyectada por el filtro al sistema de potencia se denota como i _fa , la cual se compara con la respectiva corriente de referencia i _a ^* obtenida por el algoritmo de compensación. La señal de error resultante, que se define como la diferencia entre i _fa e i _a ^* , se mantiene dentro de una banda de corriente de ancho fijo conocida como banda de histéresis (HB), que tiene la forma de la corriente de compensación, como se muestra en la Fig. 4.

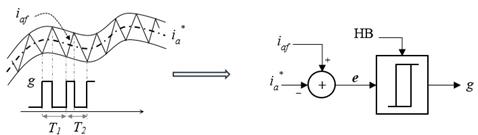
Fuente: autores.

Fig. 4 Forma de onda de la banda fija de histéresis junto con las corrientes del filtro y compensación (izquierda). Diagrama esquemático del control por banda de histéresis por fase, para producir los pulsos de activación del inversor (derecha). 

En este caso se selecciona una banda fija de valor HB. La lógica de control es la siguiente:

Si error < (i _a ^* - 0.5HB) entonces g = 1 y el interruptor superior se activa.

Si error > (i _a ^* + 0.5HB) entonces g = 0 y el interruptor superior se desactiva.

donde g es la señal de activación del transistor superior de la fase a. La señal de activación del transistor inferior se obtiene con una lógica inversa de la señal de activación del transistor superior, para no cortocircuitar el voltaje de CC del inversor. Cuando g = 1, se aplica +V _cc a la salida del inversor que hace que la corriente i _f aumente, y cuando g = 0, entonces se aplica -V _cc para reducir i _f . De esta forma se mantiene el error de corriente dentro de la banda de histéresis. Sin embargo, el periodo de la señal de activación g es variable, T ₁ ≠ T ₂ en la figura 4, lo que produce una frecuencia de conmutación variable en los semiconductores del inversor.

2.6 Control PWM por banda adaptativa de histéresis

En Fig. 5, se muestra el comportamiento de esta técnica, donde se indican dos periodos de la señal de activación g, y se indica cómo el ancho de la banda se actualiza en cada periodo de la señal g para obtener una frecuencia de conmutación constante.

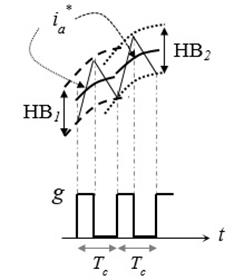
Fuente: autores.

Fig. 5 Esquema de control de corriente PWM por banda adaptativa de histéresis. El periodo de la señal de conmutación Tc se mantiene constante. 

En esta técnica, el ancho de la banda HB se modifica en cada periodo de conmutación T _c , para obtener frecuencia de conmutación constante f _c .

El valor HB se determina según la ecuación (13), y se ingresa al comparador de histéresis para generar la señal de activación por fase de los semiconductores del inversor. En ^[21] se realiza el análisis de la ecuación (13).

donde v _f es la tensión de fase e i ^* es la corriente de referencia para la misma fase. Información más detallada de esta técnica se encuentra en ^[7], ^[21].

2.7 Control PWM basado en modulación por vector espacial y banda fija de histéresis

En la modulación por vector espacial o Space Vector Modulation (SVM), el inversor opera en uno de los ocho vectores de conmutación definidos por el estado de los seis semiconductores de potencia. Cada vector se representa con tres digitos binarios (uno asociado a cada rama del inversor) como se muestran en la Fig. 6 (Dos vectores son nulos y se encuentran en el origen V ₇(0,0,0) y V ₈(1,1,1)). Con los posibles estados de conmutación se obtiene el espacio vectorial definido por seis regiones (sextantes). Según la región en la que se ubique el vector de referencia, se seleccionan los vectores de conmutación, luego el vector de referencia V _k se descompone en las proyecciones sobre los vectores adyacentes V ₁ y V ₂. La aplicación de los vectores de espacio adecuados en cada estado disminuye la frecuencia de conmutación.

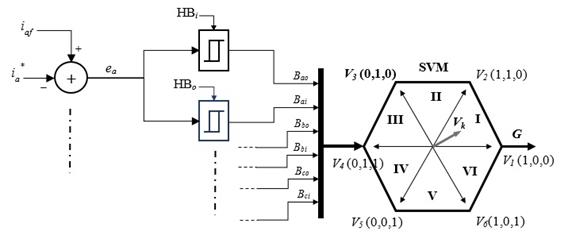
Fuente: autores.

Fig. 6 Diagrama esquemático del control PWM basado en SVM y banda fija de histéresis. 

En ^[22] se propone una técnica PWM basada en SVM y banda fija de histéresis. La modulación por banda fija de histéresis permite obtener información previa de los vectores de espacio de conmutación adyacentes según el error de corriente. Dos conjuntos de estados cada uno constituido por tres elementos, son necesarios para implementar el comparador por banda de histéresis propuesto.

Un conjunto está asociado a una banda de histéresis superior HB _o y el otro conjunto a una banda inferior HB _i , las cuales determinan la tolerancia admisible en el error de las corrientes de fase que inyecta el inversor en el PCC. Los estados de la banda superior se definen como {B _ao , B _bo , B _co }, mientras que los estados de la banda inferior se denotan como {B _ai , B _bi , B _ci }. Estas señales son la entrada de un circuito lógico que define las señales de conmutación de los semiconductores del inversor para generar el voltaje de referencia V _k , según la Tabla 1.

Tabla 1 Generación de los pulsos de disparo de los semiconductores del inversor, usando la técnica PWM de control de corriente por SVM y banda de histéresis. 

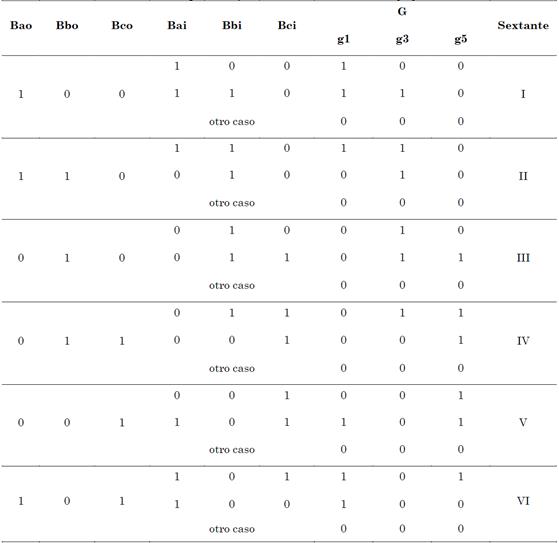
Fuente: ^[22].

Las variables lógicas {g ₁, g ₃, g ₅} forman el vector de estados de salida G, y se relacionan con las señales de disparo de los semiconductores de potencia de cada rama del inversor (uno por fase), para sintetizar el voltaje deseado de salida V _k .

El espacio solución de la técnica SVM es un hexágono dividido en sextantes de acuerdo con la ubicación del vector de referencia. El valor de B _ao, B _bo, B _co (primeras tres columnas de la Tabla 1) definen el sextante correspondiente. Mientras que los valores B _ai, B _bi, B _ci (siguientes tres columnas) están asociados a los vectores de espacio adyacentes del sextante seleccionado y las columnas g ₁, g ₃, g ₅ son los vectores de conmutación del inversor para el siguiente período de muestreo.

3. RESULTADOS Y DISCUSIÓN

En la Fig. 7 se presenta el diagrama unifilar del circuito eléctrico de potencia implementado en el programa de simulación Matlab/Simulink, para evaluar el desempeño de las tres técnicas de control por PWM implementadas. Los parámetros del circuito de la Fig. 7 se ajustaron a partir de valores reportados en las referencias ^[22], ^[23].

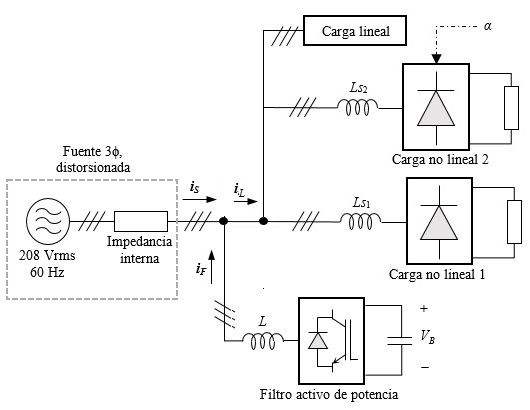
Fuente: autores.

Fig. 7 Diagrama unifilar del circuito eléctrico de potencia empleado en la simulación. 

La red de alimentación del circuito de potencia es una fuente trifásica de tensiones distorsionadas con un THD de 6,34 %, como normalmente se encuentra en la práctica. Los voltajes de fase de la fuente de alimentación se rigen por la ecuación (14), tal como se expuso en ^[24].

La componente fundamental de los voltajes de fase tiene un valor eficaz de 120 V y una frecuencia de 60 Hz, tiene armónicos a frecuencias 3ω, 5ω, 7ω y 11ω, donde ω = 2π60 rad/s. El tercer armónico tiene una amplitud de 1,18 % respecto de la amplitud de la componente fundamental, el quinto armónico de 5,98 %, el séptimo de 1,44 % y el armónico once de 1 %. La fuente de alimentación se ha modelado considerando una impedancia de corto circuito, la cual consiste en una resistencia en serie con una inductancia, el valor de la resistencia es de 20 mΩ y el de la inductancia de 0,2 mH.

Se han considerado dos cargas no lineales y una carga lineal, las cuales se conectan y desconectan del sistema de potencia durante diferentes intervalos de tiempo en la simulación. La carga no lineal 1 está compuesta por un rectificador trifásico de diodos, con una carga resistiva de 5 Ω en el lado de CC y una inductancia L _s1 de 1 mH en la entrada del rectificador, para reducir los huecos de tensión en las tensiones de línea que produce la operación del mismo. La carga no lineal 2 consiste en un rectificador trifásico de tiristores activados con un ángulo de disparo de 60°, el cual alimenta una carga resistiva de 4 Ω, a la entrada tiene tres inductancias por fase L _s2 de 1 mH para reducir el ruido que genera su operación en las tensiones de fase y de línea. La carga lineal es una carga trifásica con factor de potencia en atraso, tiene una potencia activa nominal de 3 kW, una potencia reactiva nominal de 1 kVAR y un voltaje de línea nominal de 208 V eficaces.

La simulación se realizó en MATLAB R2017a, usando el método de solución ode23tb (stiff/TR-BDF2) de paso variable, un tiempo de arranque de 0s y un tiempo de parada de 10/60 s, con un paso máximo entre muestras de 1/60000 s y tolerancia relativa de 1e-3. Los restantes parámetros de la simulación se han dejado en los valores que vienen por defecto en Simulink.

En la Fig. 8 se muestran 10 ciclos de la forma de onda de la tensión y la corriente de la fase a en la fuente de alimentación, sin la conexión del filtro activo de potencia. Al iniciar la simulación la carga no lineal 2 y la carga lineal están desconectadas, luego en cinco ciclos de la tensión de la red se desconecta la carga no lineal 1 y se conectan simultaneamente la carga no lineal 2 y la carga lineal.

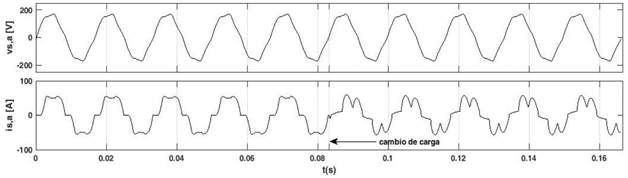
Fuente: Autores.

Fig. 8 Formas de onda de las tensiones trifásicos línea a neutro (a) y las corrientes de línea trifásicas en la carga (b). 

Se observa en la Fig. 8 la distorsión que tiene la forma de onda de la tensión de fase y la corriente, el THD de la forma de onda de la tensión es de 6,34 % y 19,44 % antes de 5/60 s y 31,73 % después, al hacer el cambio en la carga.

Usando el algoritmo de la teoría pq que se describe en el marco teórico, se obtienen las corrientes de compensación trifásicas. Las cargas trifásicas consideradas producen corrientes de línea que tienen la misma forma y un desfase entre ellas de 120°. En la Fig. 9 se muestra la corrientes de compensación para la fase a, suponiendo que V _B se mantiene en el valor de referencia. Esta corriente es la que debe de inyectar el SAPF a la red de alimentación para reducir su contenido armónico.

Fuente: autores.

Fig. 9 Corrientes de compensación en la fase a, obtenida con el algoritmo pq (a) y la derivada respecto al tiempo de la corriente de compensación (b). 

Se debe ajustar la constante proporcional k _p del control de la tensión continua del inversor con la ecuación (12), antes de conectar el filtro activo de potencia a la red de alimentación. Con los valores de C _dc , V _B,ref y la frecuencia de la red fijados previamente en 1200 µF, 300 V y 60 Hz respectivamente se obtiene para k _p un valor de 54. Se han utilizado los bloques IGBT/Diode de Simulink para modelar los dispositivos semiconductores de potencia de estado sólido que conforman el inversor, los parámetros de entrada para este bloque corresponden a los valores por defecto, es decir, una resistencia en conducción de 1e-3Ω , y para la red Snubber una resistencia de 1000 Ω en serie con un condensador de 0,1 µF. El algoritmo de control se ejecuta en cada paso de la simulación, el cual es variable y ajustado con un valor máximo de 1/60/1000 s.

Para comparar el desempeño de las técnicas PWM empleadas, se utiliza la siguiente notación, la técnica 1 corresponde a PWM basada en SVM con banda fija de histeresis, la técnica 2 hace referencia a PWM por banda fija de histéresis y la técnica 3 representa la técnica PWM por banda adaptativa de histéresis. El filtro activo de potencia se conecta al sistema en 1/40 s, con el fin de conocer el desempeño de las técnicas PWM en el transitorio de arranque. En la Fig. 10 se muestran 10 ciclos de la corriente en la fase a, para las tres técnicas consideradas.

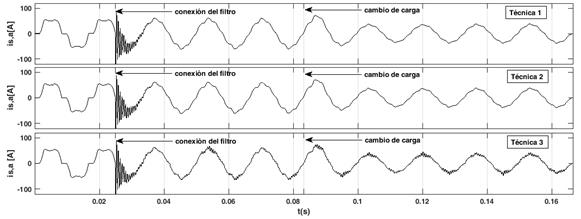
Fuente: autores.

Fig. 10 Forma de onda de la corriente en la red de alimentación después de la conexión del APF, operando con las diferentes técnicas PWM. 

Según las formas de onda de la corriente de la Fig. 10, con las tres técnicas PWM utilizadas se obtienen los mismos transitorios de arranque cuando se conecta el filtro activo de potencia. En la Tabla 2 se muestra el valor eficaz de la corriente en una de las fases de la red de alimentación, el THD_i en las corrientes de la red de alimentación, el valor eficaz o rms de la componente fundamental de las corrientes y la potencia activa en la fuente de alimentación, con las tres técnicas PWM utilizadas.

Tabla 2 Análisis comparativo de los resultados más significativos obtenidos con las tres técnicas PWM utilizadas. 

Fuente: autores.

Según los resultados obtenidos, todas las técnicas PWM reducen significativamente el THD de las corrientes de la red de alimentación. Los resultados más significativos son de 19 % a 7,2 % antes de 83 ms con la técnica 1 y de 31,7 % a 6,36 % después de 83 ms para la técnica 2. La técnica 3 presenta el desempeño más bajo en la reducción del contenido armónico. También se aprecia un incremento en la potencia activa de la red de alimentación debido a la energía que requiere el filtro activo de potencia para regular la tensión en la barra de continua del inversor.

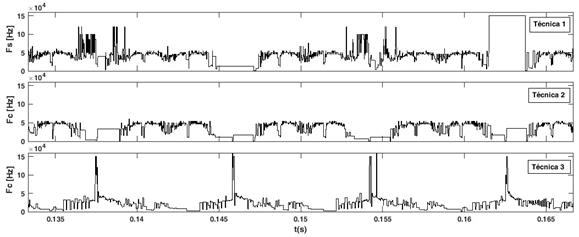
Otro aspecto que es importante considerar es referente a la frecuencia de conmutación de los tres métodos PWM. En la Fig. 11 se muestra la evolución de la frecuencia de conmutación de los semiconductores de potencia del inversor en dos ciclos de la tensión de la red de alimentación, con cada una de las técnicas PWM.

Fuente: autores.

Fig. 11 Frecuencia de conmutación de los semiconductores de potencia del inversor, obtenida con los métodos PWM utilizados. 

Los valores promedio de las frecuencias de conmutación se han calculado en un intervalo que comprende los últimos dos ciclos de las tensiones de red y son 37,9 kHz para la técnica 1, 35,47 kHz para la técnica 2 y 22,75 kHz para la técnica 3. Aunque la técnica 3 no mantiene constante la frecuencia de conmutación, es la que presenta el menor valor promedio y por ende las menores pérdidas de energía por conmutación. Su forma se aleja de ser una señal constante que es lo que se pretende con esta técnica, debido al rizado presente en la tensión del bus de CC del inversor VB. Las otras dos técnicas muestran un amplio rango de variación de la frecuencia de conmutación, la técnica 1 muestra un rango de [0,47-120] kHz y la técnica 2 de [0,786- 60] kHz.

En la Fig. 12 se muestra la forma de onda de para V _B , con cada una de las técnicas consideradas. Se puede observar que un controlador proporcional regula alrededor del valor de referencia ajustado en 600 V la tensión del bus de continua del inversor y su funcionamiento es similar para las tres técnicas de PWM utilizadas.

Fuente: autores.

Fig. 12 Tensión en el elemento almacenador de energía del inversor, para los métodos PWM utilizados. 

4. CONCLUSIONES

Según los resultados obtenidos, todas las técnicas PWM utilizadas para controlar la corriente de inyección de los APF reducen notablemente el contenido armónico de las corrientes de la red de alimentación, con resultados similares entre ellos. Si se considera la simplicidad en la implementación como criterio de selección, el método por banda fija de histéresis es el más conveniente. Sin embargo, si el objetivo es reducir las variaciones de la frecuencia de conmutación, el método PWM por banda adaptativa de histéresis es el que mejor resultados presenta. La técnica de modulación SVM tiene como principal característica considerar el inversor como una unidad, para sintetizar una señal de referencia con el menor número de conmutaciones posibles. Aunque al definir la señal de referencia a partir de la máxima variación que puede tener el error de la corriente de inyección limitada a una banda de tolerancia fija, se obtiene una frecuencia de conmutación altamente variable. Como trabajos futuros se recomienda considerar otra manera de definir la señal de referencia del método de PWM basado en SVM, para reducir la frecuencia de conmutación del inversor.