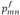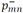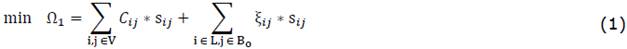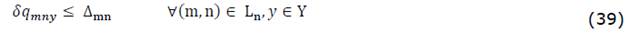1. INTRODUCTION

The Vehicle Routing Problem with Backhauls (VRPB) can be defined as the problem of determining a set of vehicle routes visiting all customer vertices, which are partitioned into two subsets. The first subset contains the vertices of the linehaul customers (LCs), each requiring a given quantity of product to be delivered. The second subset contains the backhaul customers (BCs), where a given quantity of inbound product must be picked up and transported to the depot. The objective of the VRPB is to determine a set of routes visiting all the customers in order to satisfy the demand for goods. In such case, the vehicles must first serve customers with delivery requirements before those with collection requirements. This customer partition is extremely frequent in practical situations in which a permanent reorganization of the transported goods is avoided and linehaul customers have a higher priority.

Because the VRPB is a NP-hard problem ^[1], many heuristic processes are appropriate to solve it and, therefore, most existing literature on the VRPB is related to heuristic and metaheuristic methods with high-quality results. Two comprehensive reviews of metaheuristic techniques for the VRPB are found in ^[2].

Goestschalck and Jacobs-Blecha ^[3] developed an integer programming formulation for the VRPB by extending the Fisher and Jaikumar formulation ^[4] to include pickup points. They develop a heuristic solution algorithm for this problem which, in turn, is split up into three subproblems. The first two subproblems correspond to clustering decisions for delivery and pickup customers, which are independent, generalized assignment problems. The third subproblem solves the K-independent TSP composed of delivery and pickup customers, considering the preceding constraints. The latter impose a dependency relationship on all the model’s components.

The first exact method was reported by Toth and Vigo in ^[5]. They introduced an effective Lagrangian bound that extends the methods previously proposed for the capacitated VRP (CVRP). The resulting Branch-and-Bound algorithm is able to solve problems with up to 70 customers in total. The second exact method was proposed by Mingozzi, Giorgi, and Baldacci in ^[6]. They presented a set-partitioning-based approach, and the resulting mixed-integer linear programming (MIP) is solved through a complex procedure. The results show that the approach solves undirected problems with up to 70 customers. Toth and Vigo state that no exact approaches have been proposed for VRPB in the last decade ^[1]. In our review, we have reached the same conclusion, and new proposals for unified exact models of VRPB have not been found, since the only two existing proposals are used to derive the relaxations on which the exact approaches are based ^[5].

With the progress of technology and ecological concerns, electricity has become a solid option to replace fuel. Electric Vehicles (EVs) are considered an alternative to be implemented in the transportation sector because of their numerous advantages, such as the decrease of the emission of greenhouse gases, the reduction of the dependence on fossil fuels and the little noise they generate. However, EVs still have some issues associated with battery autonomy, since this technology needs to be more mature and charging stations are not yet massively installed. Thus, the problem of the integrated planning of routes and charging stations has grown in importance in the transportation industry in recent years (^{[7][8][9][10] [11]}).

Several companies have already deployed electric delivery truck fleets. Generally, suchfleets are made up of the kind of medium-duty commercial delivery trucks that are often used to deliver supplies to customers within one locality. This job is particularly well-suited for electric trucks for several reasons: daily routes are often exactly the same (which means that range needs are fixed and predictable) and the vehicles always return to a charging station at night (making re-charging easier).

In the context of VRP, Conrad and Figliozzi ^[12] introduced the recharging vehicle routing problem (RVRP), where vehicles with limited range are allowed to recharge at customer locations mid-tour. The problem is introduced as a capacitated recharging vehicle routing problem (CRVRP) and as a capacitated recharging vehicle routing problem with time windows (CRVRP-TW). Goeke and Schneider ^[13] proposed the Electric Vehicle Routing Problem with Time Windows and Mixed Fleet (E-VRPTWMF) to optimize the routing of a mixed fleet of electric commercial vehicles (ECVs), which assumes energy consumption to be a linear function of the distance traveled and the recharging times at stations by time windows. Arias et al. ^[11] presented a probabilistic approach for the optimal charging of electric vehicles (EVs) in distribution systems, where the costs of both demand and energy losses in the system are minimized subject to a set of constraints that consider EVs’ smart charging characteristics and operational aspects of the electric network. The costs of electric delivery trucks and their conventional diesel counterparts were compared by Feng and Figliozzi ^[14]. They developed a model that integrates routing constraints, speed profiles, energy consumption and vehicle ownership costs. The location of charging stations is presented by Schiffer and Walther in ^[15], where an objective function is taken into account to minimize not only the traveled distance but also the number of vehicles needed, the number of charging stations and total costs.

Some studies analyze the actual use of EVs in commercial fleets from the standpoint of maximum necessary range autonomy of the battery to cover most trips. The data in another work ^[16] suggests that about 90% of the mobile days could be covered with an EV range of 60 km and nightly recharging. They show a daily mobility far below their maximum range with long parking hours at night. Consequently, there is no need for fast-charging.

Despite the benefits of EVs in the transportation sector outlined above, their main issues stem from the high cost of EVCS implementation, the non-standardization of the battery models and their rent cost (in the case of battery swap stations), which can be more expensive than using vehicles powered by internal combustion engines ^[17]. Additionally, these new loads have an impact on the existing distribution network (DN), as the latter was not primarily designed to support them. Some of the problems of EVCS installation in the DN are associated with outages, load shedding, overloading wires and transformers, power loss increase and degradation in the voltage profile.

Due to the considerations described above, network operators have two options to implement. The first one addresses a load management control for EVs. The second alternative is related to the distribution planning for the normal support of the new loads ^[18]. This study is more suitable to contribute to the second approach, as the optimal location of charging stations and the evaluation of the DN operation in terms of the power losses constitutes a relevant tool for future investments in the DN.

Multiple works have been developed around EVs and their impact on DNs in the context of stability, chargeability, power electronics and power quality. These problems have emerged from the wrong sizing and siting of the EVCSs. In 2014, Franco et al. ^[19] proposed a non-linear programming model to represent hybrid EVs charging in distribution systems, with the consequent reduction of power losses. Xu and Chung ^[20] presented an improvement in the reliability of the DN with the incorporation of EVs and their contribution in different performance models. They proposed two load topologies: centralized and disperse. In the context of ensuring the operation of the DN (minimizing power losses), Franco et al. ^[21] presented a linear model for radial power distribution system planning, locating and upgrading substations and wires along the planning stages, keeping the normal system operation and complying with the limits nodes voltage, chargeability and minimum losses. Shi et al. ^[22] studied an integrated model for EV charging and routing taking into account the congestion of power and transportation networks.

The increase in the economic benefit for the logistics company and the distribution operator could imply a conflict around their own interests, as the former aims to serve its customers in such a way that operational costs are minimized regarding the distance traveled. Furthermore, the location of the EVCSs, electrically far from substations, can cause more power losses and technical problems in the system. Therefore, it is necessary to find a set of alternatives to maximize the profit of both companies.

This paper proposes a multi-objective problem that models the conflict between two operators: transportation and power distribution companies. The objective of this approach is to find a set of optimal solutions (Pareto front) that minimizes the power losses in the DN and the operational cost of the VRPB with a fleet exclusively composed of EVs and using the ξ-constraint method proposed by Haimes in 1971 ^[23]. The customers with delivery requirements should not be affected by the recharge time of the battery at charging stations because the delivery of goods is the top priority. EVs must be recharged at the end of the linehaul route or in the course of the backhaul route. Additionally, the recharge should take place after the EV has covered a predefined minimum distance in order to make the most of the initial state of charge of the battery. We have called this the Electric Vehicle Routing Problem with Backhaul and optimal operation of DN (EVRPB-DN). Said problem is formulated as a mixed-integer linear programming (MILP). The main characteristic of the proposed model is that the topological configuration of the solution is taken into account to efficiently eliminate the possibility of generating solutions composed of subtours, and the operation of the network model is evaluated by means of a linear power flow.

The rest of the paper is organized as follows. Section 2 presents the formulation of the problem along with the corresponding nomenclature for the variables and parameters used in the mathematical model; also, we describe the new mixed-integer linear programming (MILP) formulation model considering some development conditions. Section 3 contains a computational study conducted in new proposed instances for the EVRPB-DN. Finally, the conclusions are presented in Section 4.

2. MATHEMATICAL MODEL FOR EVRPB-DN

This section outlines the mathematical model proposed for the EVRPB. Its objective is to minimize the distance traveled by the freight EVs to visit customers in a transportation network. As there is a restriction provided by the battery capacity, charging points (CPs) are located to virtually increase EVs’ travel range and be able to meet customers. The EVRPB can be defined as the following graph theoretic problem. Let G=(V,A ) be a complete and directed graph, where V = {0} ∪ C _𝑢 is the vertex set and A is the arc set. The vertex 0 denotes the depot and set C_𝑢 represents the feasible customers that the EV can visit once it leaves the depot. Customers include the set of linehaul customers (LCs), backhaul customers (BCs), and the charging points (CPs), represented by {L,B,K} respectively. Thus, in C_𝑢 = L ∪ B ∪ K$.

Each vertex 𝑗 ∈ C_𝑢 is associated with a known non-negative demand of goods D_𝑗 to be delivered or collected. The depot has an unlimited fleet of identical vehicles with the same positive load capacity, denoted as Q and the same electric capacity, denoted as E ^𝑚𝑎𝑥.

In the EVRPB-DN, the DN is defined by an electrical system represented by a single-line diagram H = (N, L𝑛), where N is the set of electrical nodes and L𝑛, the set of lines. Nodal voltages and currents through the lines are the state variables for the evaluation of the Kirchhoff laws. In the proposed model, the square of these variables is used to guarantee the linearity of the objective function (network losses).

The active power losses associated with the Joule effect due to wire heating are computed with the resistance R_𝑚𝑛. Likewise, it is proceeded with the reactive power losses using X_𝑚𝑛. The power consumed by the EVs, , is a variable that must be considered in the power balance.

2.1 Nomenclature

Sets

L Linehaul customers. L={1,..n}

B Backhaul customers. B={n+1,..m}.

K Charging points. K={m+1,..,m+k}.

L0 Linehaul customers and depot. L U 0

B0 Backhaul customers and depot B U 0

Cu Linehaul and backhaul customers, including the charging points L U B U K

V Transportation network vertices

N Electrical nodes

Ln Electrical lines of the system

O Candidate charging points

Parameters

C Distance between nodes i and j

D Non-negative quantity of product to be delivered or collected (demand) at the customer’s location.

KL Minimum number of vehicles needed to serve all linehaul customers

KB Minimum number of vehicles needed to serve all backhaul customers

Q Goods capacity of the vehicles

Emax Electric capacity of the vehicles’ battery (identical vehicles)

T Time needed for full EV recharge.

Unom Square of the nominal voltage of the system

Umax Maximum allowable voltage in the system

Umin Minimum allowable voltage in the system

Imax Maximum allowable current flowing through the line (m,n)

∆mn Maximum discretization interval.

𝜆 Proportion of active power consumed by the vehicle

𝜑 Proportion of reactive power consumed by the vehicle

Ps𝑛 Maximum active power supplied by the current substation

Ps𝑛 Maximum reactive power supplied by the current substation

𝜓𝑖 Gap between a candidate for EVCS respect and a transportation node

R𝑚𝑛 Resistance of the line (m,n)

X𝑚𝑛 Reactance of the line (m,n)

Z𝑚𝑛 Impedance of the line (m,n)

𝜙 Linear ratio between the distance that the EV can travel and the power

Variables

𝑆𝑖𝑗 Binary decision variable for the use of the path between nodes I and j

ℰ𝑖𝑗 Binary decision variable for the use of the path between nodes I ∈ L and j ∈ B

𝑙𝑖𝑗 Continuous variable indicating the amount of goods transported between nodes i and j

𝑝𝑖𝑗 Distance accumulated by the electric vehicle from the depot to the arc (i, j)

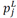Auxiliary variable that indicates the distance between linehaul customers

𝛾𝑖 Binary decision variable that indicates whether node i ∈ K is a candidate for charging point

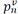Power demanded by the EV at node n

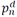Active power demanded at node n ∈ N

Reactive power demanded at node n ∈ N

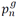Active power delivered by a substation at node n ∈ N

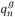Reactive power delivered by a substation at node n ∈ N

Active power flowing through the line (m,n)

Reactive power flowing through the line (m,n)

Auxiliary variable to obtain

Auxiliary variable to obtain

Auxiliary variable to obtain

Auxiliary variable to obtain

Discretization variable of the interval y ∈ Y for the variable

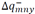Discretization variable of the interval y ∈ Y for the variable

𝑖𝑚𝑛 Square of the current flowing in he line (m,n)∈ Ln

𝑈𝑚 Square of the voltage at node m ∈ N

The basic version of the VRPB must satisfy the following conditions:

Each vertex must be visited exactly once during a single route. That is, each vertex is grade 2.

Each route starts and ends at the depot.

Each customer must be fully served when visited.

All customers are served from a single depot.

The vehicle’s capacity should never be exceeded in the linehaul or backhaul routes, and all the vehicles have the same cargo capacity.

In each circuit, linehaul vertices precede backhaul vertices (precedence constraint).

In the EVRPB, when the electric vehicle completes the linehaul route, the driver can consider several alternatives: (i) starting the backhaul route, (ii) returning directly to the depot, or (iii) resting at the charging point and recharging the battery in slow mode until the next day. The EVRPB must, additionally, satisfy the following conditions:

Each charging point (CP) must be visited by one or more routes or never be visited at all. The electrical capacity of the battery is assumed to depend on the distance traveled. The EVs are fully charged in the depot and at the charging points.

The charging points in a route are used, if necessary, in order to recharge the battery of EVs after linehaul customers or during the course of the backhaul route.

In the EVRPB-DN, EVs are supposed to start working at the same time; therefore, the charging will be carried out in the same time interval considering the following aspects:

The costs associated with DN planning are ignored in the long term; only the operation of the DN is considered.

The DN will be affected by the EV recharge during just an interval of time, according to the recharge mode [¹⁷]. In this case, a fast charging mode with a duration of 2 to 3 hours is considered.

The candidate charging points are known; the installation of all of them costs the same, which is not considered in the operation model.

The transformer at the substation is equipped with TAPS to keep the voltage at 1 pu.

The power flow to obtain the DN’s operating point corresponds to a one-phase equivalent circuit; therefore, the network is considered to be symmetric and balanced.

The EVCSs can be public; this is, they are private for the freight EVs and public when said vehicles are not recharging.

The chargeability limit of the lines and transformers in the substation is 100%. The voltage regulation should be in the ±10 V range. The active power losses associated with Joule effect due to the wire heating are computed with resistance R𝑚𝑛. Likewise, it is proceeded with the reactive power losses using X𝑚𝑛.

The power consumed by the EVs, 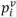, is a variable that must be considered in the power balance along with the proportions for active and reactive power 𝜆 and 𝜑, respectively.

The operation of the DN must be ensured with the current and voltage limits I𝑚𝑎𝑥 and U𝑚𝑎𝑥, respectively. The DN operation is evaluated with the costs of power losses, which are found using a linearized power flow proposed in the method described by Franco et al. [²¹]. This approach is also used by Pozos et al. in their expansion plan for distribution systems [²⁴].

The following linear mathematical model describes the evaluation of the transportation and distribution networks with objective functions Ω1 and Ω2, respectively.

This mathematical model corresponds to a multi-objective approach, which is comprised of two objective functions, (Ω1, Ω2) The first objective function (1) minimizes the distance traveled, composed of two terms. The first term corresponds to the sum of the total travelling cost of the routes used to deliver and collect the goods and visit the charging points. The second term corresponds to the use of tie-arcs connecting the last customer of a linehaul route with the backhaul customer, the charging point or the depot.

The second objective function (2), quantifies the energy losses through the distribution lines during T, i.e., the period of time (in hours) the EV will be connected.

The set of constraints (3)-(7) allow to model the OVRP for linehaul routes, where (3) imposes the connectivity requirements. In the optimal solution of the OVRP, each route has an arborescent configuration formed by a minimum spanning tree starting from the depot, spanning all the nodes, and ending at a customer. This subproblem has been called the Linehaul Open Vehicle Routing Problem (LOVRP).

In the context of the vehicle routing problem, the necessary condition to obtain a minimum spanning tree is that the number of arcs be equal to the number of customer nodes. However, this constraint is necessary but not sufficient because there may be customer nodes with a greater-than-two degree, and disconnected solutions can be obtained.

A spanning tree becomes a subgraph formed only by Hamiltonian paths if each customer node has a degree equal to or less than two. Therefore, another necessary condition is given by the set of degree constraints (4) and (5). The indegree constraints (4) dictate that exactly one arc directs to each customer node and, consequently, the outdegree constraints (5) impose that exactly one arc leaves each LC, considering two situations: (i) from a LC, a tier-arc can go to a BC or to the depot and (ii) an arc can only reach a LC from another LC or the depot. Constraint (6) is an upper limit defined by the capacity of the vehicle to transport a quantity of product over any linehaul-arc, while (7) limits the minimum number of vehicles used in linehaul routes. However, the addition of these degree constraints in directed graphs may not represent a spanning tree, because a disconnected graph can be obtained.

The addition of a flow balance constraint by each customer node avoids finding disconnected solutions, since an infeasible solution is obtained when the goods leaving the depot cannot reach the LCs. Thus, the set of constraints reported in (3) guarantees network connectivity through the flow conservation constraint for each LC, so that they are fully served when visited. Similarly, constraints (14) and (25) guarantee network connectivity through the balance of the demand flow by each BC and charging point, respectively. Note that, in constraint (25), the demand for the CP is considered to be zero.

Similar to (3)-(7), the set of constraints (14)-(18) are established for modeling the OVRP for backhaul routes. Note that constraint (19) ensures that the number of arcs leaving the depot is equal to the number of arcs entering the same. A comparison of inequalities (19) and (7) reveals that the number of linehaul arcs leaving the depot may be different to the number of backhaul arcs arriving there. This case occurs when there are tie-arcs between a linehaul route and the depot. Besides that, parameter KL limits the quantity of vehicles needed to serve the BCs.

The set of constraints (8)-(13) represents the limitations of EVs when they cross a route of LCs. Constraints (8) and (9) guarantee the fulfillment of the distance balance constraint on a LC route, which is necessary for the calculation of the accumulated distance at the moment of crossing every arc (i,j) of the optimal solution. These equations are written in a similar way to the balance of power flow but, in this case, the balance is with the distance; that is, at each node (j ∈ L), the distance of the activated arc 𝑆𝑖𝑗 is concentrated in 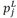, similar to parameter D𝑗 A balance with variable 𝑝𝑖𝑗 ensures that the distance is accumulated, which is the same as variable 𝑙𝑖𝑗 Similarly, the constraints in (20) guarantee the fulfillment of the distance balance constraint over a BC route; (26) and (27) do the same for the set of vertices that are CPs.

Constraints (10) and (11) ensure that, when an arc between LCs or a tie-arc is crossed, respectively, the maximum capacity of the vehicle’s battery, in terms of distance, is not exceeded. Similarly, constraints (22) and (28) verify the compliance with said electrical capacity restriction when an arc between BCs or between a CP and a BC is crossed, respectively.

Equation (12) ensures that the EV leaves the depot with the battery fully charged. The return to the depot is always done through a tie-arc or an arc coming out of a backhaul node. Therefore, constraint (13) ensures that the battery charge is sufficient to return to the depot via a tie-arc. Constraint (23) does this same verification when it is returned to the depot through an arc that leaves a backhaul node.

Equation (24) imposes that exactly one arc leaves each CP used, considering two situations: (i) that a tie-arc from an LC or BC can arrive at a CP and (ii) that, from a CP, an arc can only be connected to a BC. The direct return from a CP to the depot is not allowed since the objective is to make the most of the total charge of the EV to make a backhaul route, and not only to return to the depot. Note that this constraint is similar to (16), which imposes that exactly one arc leaves each BC visited. Two situations are considered in constraint (16): (i) an arc that arrives at a BC can only come from another BC, from a tie-arc that leaves an LC or from a CP, and (ii) an arc coming from a BC can only be connected to another BC or to the depot.

In constraint (29), 𝛾𝑗 works as a variable that recognizes the charging stations already visited. This allows to develop a mapping between the DN nodes and the transportation network vertices.

The constraints that represent the DN operation when batteries are recharged are presented in the set of equations (30)-(44). Constraint (30) is linked with (44), allowing a mapping between the physical nodes (j ∈ K) stored in variable yj and the electrical nodes (I ∈ O), to be recognized as demand points for vehicles with value (𝜙*E𝑚𝑎𝑥[W]), in the DN. Constraints (31) and (32) keep the balance of active and reactive power at each node (n ∈ N), considering the power generated at the node as well as the power that is taken and demanded from the node. Note, in both constraints, that the consumption of the vehicles is distributed with the factor (𝜆), according to the quantity of active and reactive power that is needed.

Constraint (32) represents the voltage drop in the network segment between the nodes (m,n). The set of constraints (33)-(40) is the linearization, with intervals of discretization, of the expression that relates the square of the apparent power with the summation of the square of active and reactive power. This linearization can be consulted in detail in ^[21]. In expression (33), the variable U_𝑛o𝑚 is valid since the voltage drop lies within the range of the respective energy regulation law of the country. 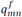The relation on the right side of the equation is summation ()² + ()².

In the set of constraints (34)-(35), the real variables ( and ) are represented by using auxiliary positive variables. Depending on the power flow, this variable can be positive or negative, and it will be taken by or , respectively, for active power, and by or 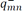or for reactive power. In addition to this, constraints (36) and (37) guarantee that the absolute value of variables |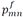|and |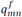| be the summation of the discretization variables. The latter are limited by constraints (38) and (39) for active and reactive power, respectively. Parameter ∆_𝑚𝑛 is calculated via equation (40), which relates the nominal parameters of the system with the quantity of discretization |Y|.

Finally, constraint (41) ensures that the only nodes able to supply power to the EVs are those selected in set O, and the set of constraints (42)-(45) allow the normal operation of the system regarding maximum allowable currents for each network segment, voltage regulation and substation capacity.

3. DESCRIPTION OF THE ℰ-CONSTRAINT ALGORITHM

One of the most widely used techniques to solve multi-objective problems is the epsilon-constraint approach, proposed by Haimes in 1971 ^[23]; it consists in the transformation of a multi-objective model into a mono-objective counterpart. The Pareto front is formed as follows:

First, each objective is individually optimized using the original constraints, thus obtaining the extreme points of the Pareto front.

The intermediate points in the Pareto front are obtained with discrete steps, varying the value ℰ between the minimum and maximum range of one of the objective functions that must be taken as a restriction (Ω₂). The other function (Ω₁) it is optimized in the same way.

4. RESULTS

The proposed model corresponds to a MILP formulation, implemented in AMPL ^[25] and solved with GUROBI 6.5 (calculated with an optimal gap option equal to 0%), with a computation time limit of 14400 seconds in a 2.4-Ghz 4-GB RAM Intel core i5-4210 computer.

To validate the proposed mathematical model using different characteristics, a modified test system was created from the set of instances in the GJ dataset published in ^[3]. Such modification corresponds to the addition of the set of charging stations K.

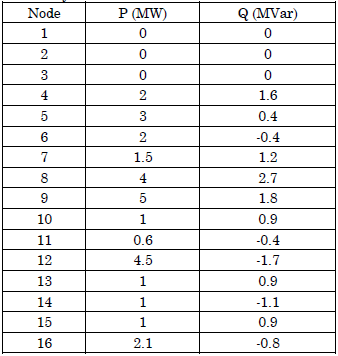
The proposed method is implemented in the modified 16-node DN presented in Fig. 1^[26]. The nominal voltage of this DN is 23 kV. The concentrated demand for each feeder is presented in Table 1.

Source: Authors’ own work.

Fig. 1 16-node distribution test system. 

Table 1 Demand of the 16-node distribution test system. 

Source: Authors’ own work.

The power losses in this distribution test system equal 0.5347 MW, with a power/distance ratio of 𝜑 = 10 The limits of chargeability in the network are randomly included (1.5 to 3 times the nominal current without the EVs). In the power flow, the demand drawn by the EVs is only active power, i.e.,𝜆 = 1.

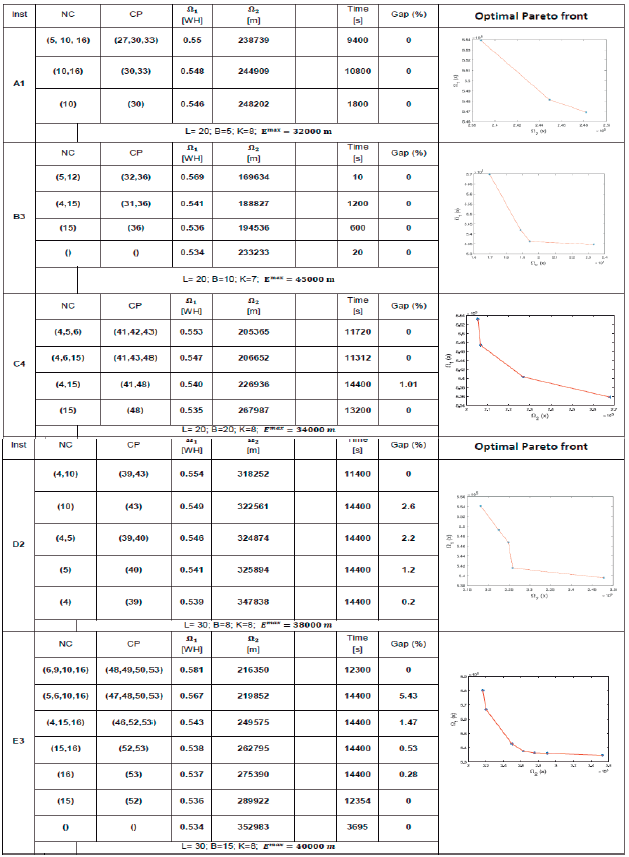
The Pareto front shown in Fig. 2 presents the solution for the instance B3 using the DN of 3 feeders and 16 nodes. Four solutions (a, b, c and d) are highlighted and described in terms of routes and the value of the objective function. The blue circles represent linehaul customers; red squares, backhaul customers; and magenta rhombuses, candidate points for EVCS installation.

Source: Authors’ own work.

Fig.2 Optimal Pareto front for instance B3. (L= 20; B=10; k=7; E^𝑚𝑎𝑥 = 45000 𝑚). 

Fig. 3 shows the routes in solution (a). Two EVCSs (big red circles) located in the DN, at nodes 5 and 12, are visited; they correspond to vertices 32 and 36 of the transportation network, respectively. In this case, the DN has its worst objective function value in terms of power losses. This is due to the fact that the EVCSs are located at nodes relatively far from the electrical substation, causing an increase of 6.7% in power losses with respect to the benchmark case.

Source: Authors’ own work.

Fig. 3 Solution (a) of the Pareto front. 

The routes of points (b) and (c) are described in Fig. 4 and 5, respectively. The charging points installed in them are closer to the electrical substations, but the distance of the routes to meet the demand for merchandise is greater than in point (a). This causes the increase in the objective function of the VRPB.

Source: Authors’ own work.

Fig. 4 Solution (b) of the Pareto front. 

Source: Authors’ own work.

Fig. 5 Solution (c) of the Pareto front. 

Lastly, Fig. 6 presents another extreme point of the Pareto front with no EVCSs installed. Consequently, the VRPB objective function value is the largest of the four solutions, but the power losses are maintained at the same level of benchmark cases.

Source: Authors’ own work.

Fig. 6 Solution (d) of the Pareto front. 

The Pareto front for other VRPB instances, using the same 16-node test system, can be observed in Table 2. NC are the mapped nodes of the distribution system that were selected for CP in the EVRPB solution. As shown, the proposed model works for different sizes of instances and it is efficient due to the low GAP. Furthermore, for other VRPB instances with more than 45 customers (instances identified as F, K, L, M, N in the literature), the solution for each objective can only be obtained with the ε-constraint method. In other words, the extreme points of the Pareto front are obtained, but the method fails to obtain the intermediate points.

Table 2 Solution to the EVRPB-DN for two instances taken from ^[3]. 

Source: ^[3]

L= Amount of Linehaul customers B= Amount of Backhaul customers K= Amount of Charge Points E^𝑚𝑎𝑥 = Electric capacity of the battery [m] NC= Charge nodes of DN CP= Charge Points in the transportation system Ω₁= Objective function of DN Losses Ω₂ = Objective function of distance traveled Time= Computational time Gap (%)= Percentage Gap

5. CONCLUSIONS

This paper proposed a novel mathematical model for the Electric Vehicle Routing Problem with Backhauls and optimal operation of the Distribution Network (EVRPB-DN) to minimize the costs associated with the operation of the transportation (adopting the VRPB approach) and distribution networks. In that sense, the two objective functions of said networks are in conflict, which is solved by using a multi-objective approach to determine the set of solutions in a Pareto front, which allows decision makers to select the most appropriate point based on their needs. The results of the EVRPB-DN in this work show good quality solutions for instances with 45 customers, 8 charge points (instance E3) and the same DN of 16 nodes.

The EVRPB-DN is a highly interesting approach for logistics companies that require pickup and delivery services. Nevertheless, the operator of the distribution network must ensure a normal power supply for end users in spite of the additional loads that EVCSs represent. Such EVCSs should be installed in accordance with the expansion plans to overcome likely operational problems. The selection of one point in the Pareto front is determined by a possible negotiation between the parties (network operator and logistics company), taking into account that the extreme points in the front are much more beneficial for one or the other.