1. INTRODUCCIÓN
La energía ha sido un factor fundamental en el desarrollo de los diferentes sectores económicos. Esta proviene, principalmente, de fuentes convencionales, tales como el petróleo, el carbón y el gas natural. Sin embargo, dichas fuentes convencionales son no renovables, por lo que su máximo nivel de producción se alcanzará en algún momento; al respecto, aún existe controversia respecto de la fecha de llegada de su máximo nivel [1].
Por otro lado, derivado del uso intensivo de dichas fuentes convencionales, se ha incrementado la concentración de gases de efecto invernadero en la atmósfera, lo cual ha dado origen al problema del cambio climático. Por lo tanto, con base en lo anterior, así como al aumento en la demanda de energía que se pronostica, es necesario el uso de fuentes alternativas de energía que sean renovables y sustentables.
Las fuentes renovables de energía son aquellas que se presentan en la naturaleza, y que como el nombre lo indica, se renuevan de forma continua. Las energías renovables se derivan directamente del sol (térmica, fotoquímica, fotoeléctrica), indirectamente del sol (eólica, hidroeléctrica, energía fotosintética de la biomasa), o de otros movimientos y mecanismos naturales del medio ambiente (geotérmica, mareomotriz) [2]. El desarrollo continuo de las tecnologías para el aprovechamiento de las energías renovables desempeña un papel clave para contrarrestar las consecuencias del cambio climático y cumplir los objetivos que se fijaron en el acuerdo de París en 2015 [3]. Entre las fuentes renovables de energía, la biomasa puede considerarse una alternativa para satisfacer la creciente demanda energética, así como para generar productos de valor agregado. De allí que se considere que la biomasa tiene un papel clave en el desarrollo sostenible.
La biomasa se define como todo aquel material de origen biológico generado en el ciclo corto de carbono; a su vez, la biomasa puede clasificarse en comestible, no comestible, y residual. Dentro de estos tipos de biomasa destacan los residuos agrícolas, los cuales son materiales que se generan en el proceso de cultivo de diferentes especies. En los residuos agrícolas se incluyen hojas, tallos, cascarillas y/o pajas. La mayoría de este tipo de residuos no tienen un uso definido, por lo que son abandonados o quemados en los campos de cultivo; esto constituye un problema de contaminación debido a los grandes volúmenes en los que se generan, así como a su inadecuada disposición. Sin embargo, los residuos agrícolas están compuestos de material lignocelulósico y de algunos compuestos de valor agregado. Debido a ello, se han enfocado los esfuerzos en la generación de productos de valor agregado y bioenergía a partir de residuos agrícolas. Dentro de la generación de productos de valor agregado destacan estudios en los que se reporta el uso de epicarpio de mandarina como colorante natural [4], el uso de la cascarilla de arroz para la remoción de azul de metileno [5], o bien la preparación de carbón activado a partir de torta de higuerilla [6].
Por otra parte, el uso de los residuos agrícolas para la generación de energía también ha sido estudiado. La bioenergía es la tercera fuente de energía renovable más comercializada; del total de bioenergía en el mundo, las tres cuartas partes corresponden al uso de biomasa de manera tradicional [7]. La bioenergía representó aproximadamente el 8.0 % del consumo total de energía y el 5.0 % de la capacidad de generación instalada de energía mundial en 2018 [7]. La biomasa puede usarse de manera tradicional y moderna.
El uso tradicional se refiere a la combustión de biomasa como la madera, desechos animales y carbón vegetal en dispositivos no tecnificados. Por otra parte, las tecnologías modernas incluyen la conversión de la biomasa en biocombustibles líquidos (bioetanol, biodiesel), gaseosos (biogás, hidrógeno renovable) y sólidos (briquetas, pélets combustibles).
De manera particular, los pélets combustibles han ganado una gran popularidad debido a que se producen de residuos agrícolas, forestales y agroindustriales mediante un proceso relativamente sencillo, en comparación con la infraestructura requerida para producir biocombustibles líquidos y/o gaseosos. En particular, los residuos agrícolas pueden emplearse para generar biocombustibles líquidos, gaseosos y sólidos, mediante diferentes rutas de procesamiento (ver Figura 1). No obstante, dado su alto contenido de lignina, y usualmente de carbón, se recomienda su uso para la producción de biocombustibles sólidos.

Fuente: elaboración propia.
Figura 1 Rutas de conversión de residuos agrícolas para la producción de biocombustibles
Los pélets combustibles se definen como pequeños cilindros de biomasa comprimida, que pueden emplearse para generar energía eléctrica o bien calorífica. Debido a que la biomasa se comprime es posible incrementar su densidad energética. Por otra parte, el poder calorífico indica la energía ligada químicamente, y que en el proceso de combustión se convierte en energía calorífica. El poder calorífico es la propiedad más importante de los pélets combustibles, y por ello se emplea para el diseño y el control de las cámaras de combustión [8]. De acuerdo con la norma ISO 18 125 (Solid biofuels - Determination of calorific value) existen el poder calorífico superior (HHV, high heating value por sus siglas en inglés), e inferior (LHV, low heating value, por sus siglas en inglés) [9]. El HHV, o poder calorífico bruto (GHV), es el calor liberado por la combustión completa de una unidad de volumen de combustible que conduce a la producción de vapor de agua y su eventual condensación. Por otra parte, el LHV, o poder calorífico neto (NHV), no contempla el calor latente del agua que contienen los biocombustibles [9], [10].
El poder calorífico de un pélet combustible puede determinarse experimentalmente, o a partir de los resultados de los análisis elementales y/o proximales del mismo [10], [11].
El poder calorífico se determina experimentalmente mediante un calorímetro de bomba adiabática o espectroscopía de infrarrojo [8], [10], [12]-[17]. Por otro lado, el poder calorífico de los pélets combustibles puede estimarse con base en el análisis proximal de la biomasa de la que se elabora; el análisis proximal determina el porcentaje de humedad, material volátil, carbono fijo y cenizas [18].
La determinación experimental de los poderes caloríficos y de los análisis elementales requiere una instrumentación especial y costosa, mientras que los análisis proximales pueden realizarse con relativa facilidad utilizando equipos de laboratorio comunes; por ello, éstos últimos son muy atractivos para estimar el poder calorífico. En la literatura se han reportado diversos modelos para la predicción del poder calorífico empleando los datos reportados por los análisis proximales de diferentes tipos de biomasas. En 2012, [18] presentaron una revisión de los modelos matemáticos que se empleaban para predecir el poder calorífico. Los autores reportaron que existen modelos basados en análisis elemental, análisis proximal, análisis elemental y proximal, análisis estructural, análisis de propiedades físicas, análisis químicos y algunas otras variables. De acuerdo con [18], el uso de modelos basados en el análisis proximal es más sencillo y con beneficios económicos, dado que las determinaciones se pueden realizar con equipos sencillos. Dentro de estos modelos existen algunos que se obtienen sólo para un tipo de biomasa, y otros que consideran diversas biomasas.
Posteriormente, [19] presentaron un estudio que consideraba 27 biomasas de Turquía. A dichas biomasas se les realizaron análisis proximales, y se les determinó el poder calorífico. Con base en estos resultados se propusieron diversos modelos matemáticos con valores de R2 entre 0.812 y 0.832, y desviaciones mínimas y máximas de 1.469 MJ/kg y 1.493 MJ/kg, respectivamente. Por otra parte, [20] estudiaron 35 biomasas, de las cuales 31 fueron tomadas de la literatura y las cuatro biomasas restantes procedían de India.
De acuerdo con los resultados de los análisis proximal y elemental propusieron diversos modelos matemáticos considerando diferentes funcionalidades del poder calorífico con las variables de los análisis realizados, así como mediante el uso de otros modelos previamente reportados. Sus resultados muestran que existe una menor desviación estándar cuando se usan los análisis proximales, respecto al análisis elemental.
Como puede observarse, existen muchos modelos para predecir el HHV de la biomasa que utilizan los resultados del análisis proximal y elemental, así como algunos que se basan en los resultados del análisis estructural o en determinaciones químicas o físicas [8], [10], [12], [18], [20]. El uso de los resultados del análisis proximal ha ganado en importancia con el tiempo, tanto entre los investigadores como entre los ingenieros, dada la facilidad y la rapidez con la que se pueden realizar dichos análisis [8], [10], [13], [15]. En México, este tipo de estudios no han sido realizado, y es importante tener información que permita saber cuál de los modelos existentes proporciona una buena estimación del poder calorífico de las biomasas, con especial interés en los residuos agrícolas. En caso de que con los modelos existentes no se disponga de una buena aproximación, los hallazgos del presente estudio permitirían el desarrollo de un nuevo modelo para los residuos agrícolas mexicanos. Por ello, esta investigación realiza un estudio comparativo de los modelos matemáticos lineales, previamente reportados en la literatura y estimados con base en otras biomasas, para predecir el poder calorífico en residuos agrícolas procedentes de México. Se consideran sólo los modelos reportados que se basan en el análisis proximal, dada su sencillez y bajo costo.
El artículo se encuentra organizado de la siguiente manera: en la Sección 2 se presenta la metodología que se siguió para la realización del análisis proximal y poder calorífico de los residuos agrícolas procedentes de México.
Posteriormente, se presentan los resultados de los análisis proximales de residuos agrícolas previamente reportados en la literatura, así como los modelos matemáticos que serán analizados; en la Sección 3 se presenta la discusión de resultados; y la Sección 4 contiene las conclusiones.
2. METODOLOGÍA
2.1 Residuos agrícolas procedentes de México
En este estudio se utilizaron residuos agrícolas procedentes de México, así como algunos otros reportados en la literatura. En los residuos agrícolas procedentes de México se incluyen los residuos de frijol (tallo, hoja y vaina de la planta) de la especie flor de mayo (cosechas de Hidalgo, 2016 y 2019), cascarilla de arroz (cosecha de Guanajuato 2017 y de Querétaro en 2019), paja de trigo (cosecha de Guanajuato 2017) y cascabillo de café (cosecha de Oaxaca 2018 y de Querétaro 2020). Las biomasas fueron recolectadas de manera aleatoria por estudiantes de la Universidad Autónoma de Querétaro, de acuerdo con las fechas indicadas para cada cosecha. Las biomasas fueron transportadas por vía terrestre desde los sitios de generación hasta el laboratorio de bioingeniería de la Facultad de Ingeniería (Campus Amazcala) de la Universidad Autónoma de Querétaro. Las biomasas fueron procesadas inmediatamente después de haber sido recibidas en el laboratorio.
A todos los residuos agrícolas se les realizaron análisis proximales, con base en los métodos descritos a continuación.
2.1.1.1 Determinación de humedad
El contenido de humedad se define como la cantidad de agua que se encuentra presente en una biomasa en particular. La humedad de los residuos agrícolas se determinó mediante el procedimiento establecido en los métodos oficiales de la AOAC Internacional (Association of Analytical Communities) [21], [22]. Para ello, la muestra (2 g) debe calentarse a 100 ± 2 °C durante 2-4 horas en crisoles previamente llevados a peso constante; cada sesenta minutos los crisoles con la biomasa fueron pesados hasta que estos se encontraran a peso constante. Una vez que el peso de los crisoles se mantuvo constante, estos se colocaron en un desecador Numak. La pérdida de peso se reporta como humedad [21]. El horno de secado es marca Air, mientras que la balanza es marca Precisa modelo 321.
2.1.1.2 Determinación de cenizas
El cálculo de las cenizas se realizó conforme a la norma ASTM D1102-84 [22], [23]. Las muestras se colocaron en una mufla, modelo FE-361-Felisa, la cual se programó para alcanzar una temperatura de 800 °C, y en ella se dejaron las muestras por 10 horas para lograr la calcinación. Una vez que las muestras se enfriaron, se pesaron en una balanza para obtener el porcentaje de cenizas.
2.1.1.3 Determinación de materia volátil
La materia volátil se determinó de acuerdo con lo establecido en los métodos Hach [22], [24]. Para ello se colocaron 2 g de la muestra dentro de la mufla, la cual ya estaba programada a una temperatura de 550 °C, y cada 30 minutos se midió el peso hasta que este se mantuvo constante [24]; la prueba tuvo una duración aproximada de 5 horas. El horno de secado es marca Air, y se emplea una atmósfera de aire para realizar la determinación.
2.1.1.4 Determinación de carbono fijo
El contenido de carbono fijo se calcula restando de 100 la suma del contenido de humedad, materia volátil y cenizas, de acuerdo con lo reportado en [25].
2.1.1.5 Determinación del poder calorífico
El poder calorífico se determinó mediante un calorímetro isoperibólico 6200 Parr. El procedimiento consistió en elaborar pastillas, de peso máximo 1 g, con base en las muestras ya molidas con una prensa manual 2811 Parr. Las pastillas se colocaron en crisoles de calorimetría junto con el hilo de combustión; después se colocó el crisol en la bomba de combustión de oxígeno. Enseguida se cierra el equipo, se registra el peso de la pastilla y se selecciona la bomba que se llena con oxígeno para asegurar la combustión total. Después se muestra el poder calorífico en cal/g.
2.1.1.6 Análisis estadístico
Los resultados se expresaron como las medias ± la desviación estándar de al menos tres experimentos. Los datos se analizaron utilizando el software R. El análisis estadístico se realizó siguiendo el ANOVA (Fisher) y la prueba de Tukey-Kramer para la identificación de diferencias significativas entre las muestras. El nivel de significancia se estableció en p = 0.05.
2.2 Residuos agrícolas reportados en la literatura
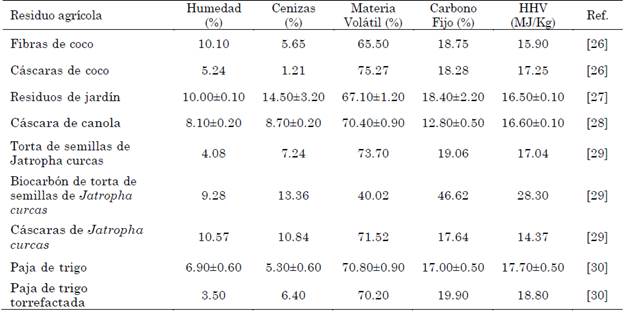
Por otra parte, para complementar los datos que serán obtenidos de los análisis proximales de los residuos agrícolas procedentes de México, se seleccionaron otros residuos agrícolas reportados en la literatura. De dichos residuos se presentan los datos reportados para los análisis proximales en la Tabla 1.
2.3 Modelos matemáticos para la predicción del poder calorífico
Como se mencionó anteriormente, existen diversos modelos matemáticos reportados en la literatura para la predicción del poder calorífico. En este estudio se seleccionaron los modelos lineales que emplean información de los análisis proximales. Si bien existen en la literatura modelos matemáticos que consideran dependencias polinomiales, se han escogido los modelos lineales por su sencillez. En la Tabla 2 se presentan los modelos seleccionados en este estudio para predecir el poder calorífico de las biomasas como función de la información brindada por el análisis proximal.
Los modelos matemáticos serán aplicados a las biomasas de estudio, y se compararán con los datos experimentales del poder calorífico reportados.
3. RESULTADOS Y DISCUSIÓN
En esta sección se presentan los resultados obtenidos en el presente estudio. En la sección 3.1 se discuten los análisis proximales tanto para residuos agrícolas procedentes de México como los reportados en la literatura. Posteriormente, en la sección 3.2 se analizan los resultados de la predicción de los modelos matemáticos empleando todas las biomasas de estudio, así como sólo las procedentes de México (Tabla 2).
Tabla 2 Ecuaciones de predicción para el HHV utilizando el análisis proximal

Nota: HHV: poder calorífico superior; MV: materiavolátil; CF: carbonofijo; ASH: cenizas.
Fuente: elaboración propia.
3.1 Métodos
Los resultados del análisis proximal y del poder calorífico (HHV) se presentan en la Tabla 3, tanto para las biomasas analizadas experimentalmente, como para aquellas reportadas en la literatura.
En la Tabla 3 se observa que los valores de humedad inicial de cada biomasa se encuentran en rangos de 4-10 %, siendo la paja torrefactada la biomasa con el valor más pequeño (3.50 %) [30], esto se debe a que el agua contenida inicialmente en la biomasa se evaporó al someterla al proceso de torrefacción [31]. El bajo contenido de humedad de las biomasas es un dato promisorio, ya que a menor contenido de humedad se espera una mayor cantidad de energía neta [32].
Por otro lado, el contenido de cenizas representa todo el material que no fue quemado, y está compuesto, principalmente, por materiales inorgánicos [33]. Debido a ello, las materias primas con alto contenido en cenizas suelen ser problemáticas durante la conversión térmica debido a los problemas asociados con la eliminación de las cenizas, la formación de escorias, la corrosión de los equipos y la formación de sedimentos en el horno [34], [35].
De las biomasas de estudio, la cascarilla de arroz presentó un elevado contenido de cenizas, lo cual tuvo un efecto negativo en el poder calorífico; cabe mencionar que este residuo tiene el menor HHV de todas las biomasas de estudio, por lo que el uso de la cascarilla de arroz como combustible requerirá de su mezcla con otras biomasas para poder así cumplir con el valor establecido para el contenido de cenizas en el estándar.
Por otro lado, el contenido de materia volátil de la biomasa alcanza hasta el 90 % en residuos como el de frijol y cascabillo de café, mientras que los valores mínimos se encuentran en el rango del 65-67 % para residuos de jardín y fibras de coco [26] [27].
El contenido de carbono fijo de la biomasa puede relacionarse fácilmente con el poder calorífico, ya que tiene un efecto positivo en el potencial energético de la biomasa; esto se puede observar en los residuos de jatropha, donde el biocarbón de la torta de semillas presentó un valor de 46.62 % de carbono fijo y un HHV de 28.30 MJ/kg [29]. Por otro lado, el contenido de materia volátil se encuentra asociado a un mayor índice de reactividad de la biomasa [22]. Sin embargo, un alto contenido de materia volátil no garantiza un alto poder calorífico, ya que algunos componentes de la materia volátil se transforman en gases no combustibles (CO2 y H2O) [19]. Lo anterior se observa en los residuos de frijol que contienen 93.66 % de materia volátil, pero su poder calorífico está por debajo de aquellos como la paja de trigo [30], cáscaras de coco [26] y tortas de semilla de jatropha [29] con menor material volátil. Del análisis estadístico se observa que las desviaciones estándar son pequeñas respecto de la media, siendo el mayor valor de 0.5 % en el caso de la humedad de los residuos de frijol; este dato porcentualmente equivale a 6.33 %. No obstante, el análisis muestra que no existen diferencias significativas entre las medias de las tres muestras analizadas.
3.2 Resultados de la evaluación de los modelos matemáticos
La Tabla 4 muestra la estimación del HHV utilizando los modelos matemáticos mostrados en la Tabla 2; estos resultados se comparan con el HHV obtenido experimentalmente para las biomasas de México y las reportadas en la literatura. En la Tabla 4 se observa que para los residuos del cultivo de frijol (1) predice mejor el HHV, con diferencia máxima de 0.38 MJ/kg, lo cual representa 2.38 %; cabe mencionar que ambos residuos son del mismo estado, pero de cosechas de diferente año. El HHV de la cascarilla de arroz se modela mejor con (4), teniendo un error máximo de 0.32 MJ/kg (2.34 %); sin embargo, en este caso (3) tiene un menor error para el residuo de Guanajuato (diferencia de 1.39 %), mientras que (4) tiene un error equiparable en los residuos de Guanajuato y Querétaro (diferencias de 2.34 % y 2.22 %, respectivamente).
Tabla 4 Comparación del HHV estimado y experimental de las biomasas de estudio (MJ/kg)

Nota: HHV: poder calorífico superior; D.E: desviación estándar
Fuente: elaboración propia.
Para la paja de trigo, la mejor predicción del HHV experimental se obtiene con (2), con una diferencia de 0.25 MJ/kg, lo cual representa una diferencia porcentual de 1.38 %; la tendencia concuerda tanto para la biomasa procedente de México como para la procedente de Chile. Esto se debe a que la paja de trigo, no procedente de México, fue empleada para la estimación de este modelo matemático. Para el cascabillo de café se observa una gran diferencia entre la predicción y el valor experimental, encontrándose las menores discrepancias en (3) y (6), con diferencias de 10.68 % y 12.5 %, respectivamente; cabe mencionar que para la variedad queretana de este residuo es (3), quien presenta un error muy grande, 12.62 %, pese a que esta biomasa fue considerada en el modelado matemático.
Para estas cuatro biomasas procedentes de México los mayores errores se observan en los modelos (5)-(8), en los cuales se consideran combinaciones entre la materia volátil, carbono fijo y cenizas; las diferencias máximas se encuentran desde valores de 3.77 %, en el caso de la cascarilla de arroz, hasta 38.37 % para el cascabillo de café. Por otra parte, (4) predice con un error aceptable la mayoría de las biomasas; este modelo sólo emplea la materia volátil y el contenido de carbono fijo, así como una débil funcionalidad indirecta del contenido de cenizas.
Es importante mencionar que la desviación promedio de (4) es 0.8784 MJ/kg, y es seguida muy de cerca por (3) con un valor de 0.8834 MJ/kg mientras que (1) tiene un valor de 0.9335 MJ/kg.
Para las biomasas obtenidas de la literatura, se observa que para la fibra de coco se podría utilizar (4), la cual presenta una diferencia de 0.42 MJ/kg (diferencia porcentual de 2.64 %) [26], mientras que, para las cáscaras de coco (1) presenta un error mínimo de 0.07 MJ/kg (0.41 %) [26]. Para los residuos de jardín, (4) presentó un error de 0.01 MJ/kg (0.06 %) [27], mientras que (2) tuvo un error pequeño, 0.04 MJ/kg, para la estimación del HHV de las cáscaras de canola [28]. Por último, para la torta de semillas de jatropha curcas y las cáscaras de jatropha curcas (5) presenta un error de 0.23 y 1.63 MJ/kg, respectivamente 1.35 % y 11.34 %, mientras que (3) presenta un error de 7.14 MJ/kg para el biocarbón de torta de semillas de jatropha curcas [29]. En el caso del biocarbón de tortas de semillas de jatropha curcas [29], el error es alto en todos los modelos, siendo el mínimo de 19.33 %; esto se debe a que en el proceso de pirolisis ocurre la degradación de la hemicelulosa y la lignina, por lo que su composición química es más parecida al carbón [36].
Para las biomasas reportadas en la literatura, en general los modelos (5) y (6) tienen las desviaciones más altas (con diferencias porcentuales desde 1.35 % hasta 104.84 %), seguidas por (7) con diferencias máximas de 58.59 %. Considerando las biomasas procedentes de otros países, (3) es la que presenta la menor desviación promedio con un valor de 1.64 MJ/kg, seguida muy de cerca con un valor de 1.7433 MJ/kg de (4), mientras que (2) y (1) presentan valores de 2.0955 MJ/kg y 2.1166 MJ/kg, respectivamente.
Considerando todas las biomasas de estudio, la Figura 2 presenta el ajuste de los datos de HHV considerando un modelo de regresión lineal por mínimos cuadrados ordinarios.
Asimismo, se presenta el coeficiente de determinación R2. De acuerdo con la Figura 2, se observa que los coeficientes de determinación para (3) y (4) fueron los más altos, con un R2 de 0.72 y 0.66, respectivamente; estos resultados son ligeramente menores que los reportados por [19], que incluyen valores de R2 entre 0.812 y 0.832, y desviaciones mínimas y máximas de 1.469 y 1.493 MJ/kg, respectivamente. Cabe mencionar que (3) considera la materia volátil y el carbono fijo, similar a (4); en ambas ecuaciones se considera una débil funcionalidad de la cantidad de cenizas, la cual es directa en (3) e indirecta en (4). Además, en (3) se obtiene a partir de un gran número de biomasas, las cuales son de diversos tipos. Por otra parte, los modelos (5)-(8) contemplan que los resultados del análisis proximal son lineales, pero el valor de HHV predicho para biomasas con alto contenido de carbono fijo tiende a disminuir.
De la Figura 2 se observa que, considerando todas las biomasas, (3) y (4) son las que mejor modelan el HHV con desviaciones promedio de 1.2614 MJ/kg y 1.3108 MJ/kg, respectivamente. Detrás de (3) y (4) se encuentra (1) con una desviación promedio de 1.5251 MJ/kg; esta tendencia es consistente con la que se observó en los valores de R2. En (3) fue obtenida considerando una gran cantidad de biomasas, al igual que (2); no obstante, (2) no considera una funcionalidad ni directa ni indirecta del contenido de cenizas, dado que solo considera al contenido de materia volátil y al contenido de carbono fijo. Por otra parte, la (3) sí considera una funcionalidad débil del contenido de cenizas de manera directa, mientras que (4) considera la funcionalidad de manera indirecta en el término independiente. Algo similar sucede con (1), en donde existe una funcionalidad ligeramente más fuerte del contenido de cenizas, con un valor menor a 0.2 en el coeficiente.
En contraparte, (5), (7), y (8) consideran una funcionalidad alta del contenido de ceniza (coeficientes mayores a 0.2), mientras que (6) no la considera. Tanto (2) como (5)-(8) presentan valores de R2 menores a 0.33; el menor valor de R2 (0.0347) se presenta en (5), la cual tiene la funcionalidad más fuerte del contenido de cenizas, con un coeficiente de 1.84. Por lo que, en el caso de las biomasas mexicanas, un modelo que considere una débil funcionalidad del contenido de cenizas permitirá predecir con menor desviación el HHV, en comparación con aquellos modelos en los que la dependencia es fuerte.
A pesar de ello, los valores de R2 son relativamente bajos, por lo que existe un área de oportunidad para el desarrollo de modelos matemáticos específicos para biomasas mexicanas, que permitan estimar con mayor exactitud el HHV considerando el contenido de materia volátil, de carbono fijo, así como una débil funcionalidad de la cantidad de cenizas.
Es importante mencionar que en la Figura 2 existe un punto experimental que destaca del resto (28.30 MJ/kg), el cual corresponde al poder calorífico del biocarbón de torta de semilla de jatropha curcas [29]. El poder calorífico de esta biomasa es más elevado, debido al pretratamiento que se le ha realizado (pirolisis). Debido a ello, se realizó un análisis de los poderes caloríficos considerando todas las biomasas con excepción del biocarbón de torta de semilla; sin embargo, en todos los casos los valores de R2 disminuyen de manera significativa, considerando tanto modelos lineales como polinomiales. Por ejemplo, para el modelo de (1) la R2 varía de 0.5558 considerando todas las biomasas a 0.1359 (modelo polinomial) y 0.0079 (modelo lineal) al remover el dato experimental del biocarbón. Una tendencia similar se observa en el resto de los modelos. Debido a lo anterior, el dato experimental del biocarbón de torta de semilla de jatropha curcas se mantuvo en el análisis.
Desde el punto de vista físico, de acuerdo con la norma ISO 18125 [9], un alto poder calorífico depende principalmente de la cantidad de carbono fijo, así como del material volátil presente en la biomasa; es decir, a mayores valores de carbono fijo y material volátil puede esperarse un mayor poder calorífico. En contraparte, el contenido de cenizas afecta negativamente al poder calorífico; o sea que, a mayor contenido de cenizas, menor poder calorífico puede esperarse. A su vez, un alto contenido de cenizas no depende sólo de la composición de la biomasa o las características del suelo donde se cultiva; el contenido de cenizas también se ve afectado por la contaminación de las biomasas durante su manejo, almacenamiento y transporte, el uso de aditivos inorgánicos, o bien su procesamiento mediante tratamientos químicos [37]. En consecuencia, el alto contenido de cenizas es un factor muy variable que no solo se atribuye a las características del suelo o naturaleza de la biomasa, sino inclusive a las prácticas agrícolas de cada país.
Por ello, cuando el contenido de cenizas es considerado con un alto peso para correlacionar al poder calorífico, puede sobreestimarlo o subestimarlo de manera significativa; esta situación es la que se presenta en los casos de estudio analizados en el presente trabajo.
De allí que la recomendación es el desarrollo de modelos que consideren el contenido de carbono fijo, el contenido de materia volátil y un término independiente; en este último término pueden agruparse los efectos de otras variables como la humedad y el contenido de cenizas.
4. CONCLUSIONES
En este trabajo se realizó un estudio comparativo de los modelos matemáticos lineales reportados para la predicción del poder calorífico con base en el análisis proximal; este estudio se realizó considerando datos de residuos agrícolas mexicanos. Los resultados muestran que, para residuos agrícolas mexicanos, el mejor modelo es aquel que considera solo el contenido de materia volátil y carbón fijo, así como una débil dependencia indirecta del contenido de cenizas. Se observa que cuando el contenido de cenizas es considerado con un alto peso para correlacionar al poder calorífico, puede sobreestimarlo o subestimarlo de manera significativa. Lo anterior se debe a que el contenido de cenizas no sólo depende de las condiciones de cultivo o composición de la biomasa, sino de otros factores relacionados con el manejo, almacenamiento y transporte de la biomasa; por ello, se sugiere considerar una débil dependencia de este factor, ya que es altamente variable y afecta de manera significativa la predicción del poder calorífico. Para los modelos reportados en la literatura se presentan correlaciones bajas para los residuos agrícolas mexicanos, por lo que el desarrollo de modelos matemáticos representa un área de oportunidad, la cual puede ser explotada con base en los hallazgos del presente estudio.