1. INTRODUCTION
The degrading effects of climate change represent a challenge to preserve environmental sustainability [1]. Opposite of that, there is an increased demand for power resources from a growing population strongly dependent on technology. This warns governments worldwide of political, economic, social, technical, and environmental concerns [2], [3]. Traditionally, power demand has been supplied by industrial models based on fossil fuels (oil, coal, and natural gas). However, their restricted availability pushes for introducing new paradigms of energy production from renewable sources [4].
Modern electric power systems range from simple distributed generation topologies (microgrids [5]- [9]) mixing several types of natural power (hydraulic, solar thermal and photovoltaic, biomass, wind, tidal and geothermal) to sophisticated intelligent schemes of grids (smart-grids). Microgrids can be of direct current (DC) or the alternating current (AC) type, depending on the requirements of the demand (load). Despite several applications for single-phase and three-phase AC systems, the number of DC grids is becoming reasonably increased [10]. From a technological viewpoint, DC microgrids are of the same nature as sources like photovoltaic (PV) arrays and battery banks. Moreover, power flow control of DC microgrids becomes easier by avoiding all technical issues regarding frequency and phase [11], [12].
On the other hand, the intermittency of renewable sources requires dynamic management rules adapting the appropriate use of available resources. In traditional large-scale generation schemes, this is called economic dispatch [13]. For microgrids, some works reported in the literature have performed formulation of costs for an optimal operation of the distributed generation system. For instance, in [14] Hoogwijk explores the potential of renewable sources and defines related generation costs; in [15] Surender et al. discuss the dispatch of energy resources in a short data frame including renewable power; in [16] Giraldo defines and analyzes optimization scenarios for the energy management of distributed generation systems. From the control viewpoint, a dispatch methodology can be implemented only after assuring desired behavior at each power source in both: single and combined operations.
More specifically, the control of isolated (or islanded) microgrids has become a subject of increasing interest for researchers in recent years, given the intricate problems associated with the erratic behavior of renewable resources. In particular, it is challenging to assure a stable and continuous power flow under environmental variations and changing load conditions. A literature review reveals that a key point to perform operational control in isolated microgrids is the state of charge of battery energy storage systems, as it is addressed by Jiechao et al. in [17]. In a similar approach, Giraldo et al. perform in [18] synchronization of isolated microgrids by communicating frequency information data for coordination via cooperative control and consensus algorithms. More interestingly, Jinrui et al. are investigating in [19] the impact of low-frequency oscillations caused by converter-interfaced distributed generators in isolated microgrids with smart loads. In [20] Liang et al. define an electric spring as an effective manner of enhancing the operational flexibility and renewable energy integration, by determining the operation status of noncritical loads. On the other hand, Ryan et al. in [21] discuss compensation of low inertia in islanded microgrids by adding a data-driven grid-supporting control system for battery energy storage systems, being similar to the approach proposed by de Matos in [22] to keep energy balance in microgrids by limiting the battery-bank state of charge under droop control strategies.
The droop control technique is a well-known method to achieve power scheduling on electrical grids being adaptable to a hierarchical structure with several levels of regulation loops. Related works include the classical paper of Guerrero et al. [23] defining the hierarchic control of microgrids. In [24] and [25] developments are presented on the application of such control topology to DC microgrids. Dispatch and control for DC microgrids are explored further in papers like [26] with a multiagent supervisory control approach; [27] focusing on the dispatch of storage units and [28] including real price constraints on DC microgrids subjected to droop control.
Hence, inspired by the developments this paper addresses the formulation and implementation of an optimal dispatch based on hierarchical droop control, over a DC microgrid including renewable resources. The approach presented here is simple but tries to illustrate in-depth the solution to the optimal management of renewable power resources by numerical analyzes performed on a simulated testbench. The paper corresponds to an extended version of the work [29] presented as an oral contribution to the X SICEL-2021.
2. THE DC MICROGRID
Figure 1 depicts the isolated microgrid selected as a case study. The system includes a series of 5 photovoltaic (PV) panels of 12 VDC / 310 W (for a total power of 1550 W / 60 VDC) in parallel with a bank of 5 batteries of 12 VDC / 250 Ah arranged in series (for a total power of 15000 Wh / 60 VDC), feeding a resistive load demanding 1500 W / 120 VDC. The connection interface between each generator (PV array and batteries) and the DC bus was performed via DC/DC boost power converters. The situation illustrated is inspired by charging units for electric vehicles in Bucaramanga - Colombia (https://www.essa.com.co).
2.1 Open-loop simulation of the microgrid
To perform a dynamical analysis of the system, an equivalent circuit for the microgrid was simulated in PSIM (https://powersimtech.com) following the schematic representation shown in Figure 2 and the circuit parameters listed in Table 1.
The simulation scenario consisted of a zero initial condition, followed by a change in load nominal value at t = 0.07 s (step variation for RL from 9.6 Ω to 12 Ω), reversed at t = 0.11 s.
In addition, a variation in the supply voltage E1 (from its nominal value of 60 V DC to 55 V DC) was included during the interval t ∈ [0.14, 0.24] s, emulating the decaying lobe of solar radiation after the noon. The corresponding results without control are presented in Figure 3 (dark trace), showing changes in load power (1500 W) as an effect of system disturbances.
3. DROOP CONTROL
To perform the power-sharing between generators, it is mandatory to achieve first the individual regulation of sources. By following ideas proposed by Utkin [30], a double-loop configuration was implemented as depicted in Figure 4 to control variables of the boost power converter, with an internal loop for the inductor current and an external loop for the capacitor (output) voltage. Parameters for the PI controllers were tuned as described in [31] using classical methods. In accordance, the gray trace in Figure 3 verifies the improvement achieved in the stationary conditions of the system according to desired nominal values.

Source: Created by the authors.
Figure 4 Double-loop regulation scheme for the boost power converter
3.1 Power sharing
Once the output values of the perturbed system have been recovered, the droop scheme presented in Figure 5 was configured with Rdi standing for the droop resistance at the i-th generator. The calculation for each Rdi was performed as presented in (1):
being ∆V the maximum deviation allowed for the DC bus voltage, Pσi = Iσi × Vσ the maximum power delivered to the load by the i-th generator, and Vσ its minimum voltage.
Hence, by assuming fixed proportions of power in (2):
The corresponding droop resistances for the microgrid (taking ∆V = 2 V and Vσ = 118 V) are: Rd1 = 0.262 Ω and Rd2 = 0.393Ω. The hierarchic structure performing the control is illustrated in Figure 6 by a block diagram including the following levels: primary control (internal loops of the converter); secondary control (adjustment given by the droop resistance) and tertiary control (power references for the lower levels). After performing simulations in PSIM for that scheme, the results presented in Figure 7 (dark trace) allow verifying the power-sharing between the PV array and the battery bank according to proportions selected in (2).
4. OPTIMAL MANAGEMENT OF RESOURCES
The results presented so far are not considering generation costs. In general, many authors consider renewable energy power as free and then as a non-dispatchable resource. However, it is possible to assign ponderation rules allowing weighted contributions for generators attending a given demand. The simplest rule is to assign the whole power available, but what about if there are several sources generating power at the same time? and how to proceed in order to mix them properly?
Based on cost models proposed by Hoogwijk in [14], it is possible to define generation costs in renewable sources by (3):
being α the annuity factor, I the investment cost per unit power P installed, and M the maintenance cost per unit power P installed. In particular, employing the information provided by IRENA (https://www.irena.org) on statistics for the year 2021, the cost functions for the PV array and the battery bank were constructed by coefficients listed in Table 2, estimating a total generation cost of the microgrid as in (4):
Further details about these calculations are given in [32] and references therein.
4.1 The optimization problem
To operate the microgrid at the lowest cost, the combination of P1 and P2 allowing the minimum of (4) is required, subjected to restriction (2) under variations on generation power, as it is shown by (5):
Among the several methods available to solve the optimization problem defined in (5), the Newton-Raphson approach proposed by Saadat in [13] was employed in this article. In accordance, by noticing that the total generation cost in (4) has a linear fashion, it is required to employ a quadratic transformation to assure the existence of a minimum (concavity). In particular, we chose the function proposed in (6):
and then minimizing Γ(P1, P2) corresponds to minimize C(P1, P2), as it can be easily shown that Γ ≥ C.
By doing so, the Lagrangian function in (7):
can be minimized by an appropriate selection of the Lagrange multiplier λ, subjected to restrictions defined in (2).
The solution for λ was approximated numerically using a predictor-corrector algorithm programmed in C language and implemented in PSIM with a Simplified C block. An equivalent pseudo-code for the optimization routine is illustrated in Figure 8. The optimized results are contrasted in Figure 7 with the non-optimized power-sharing. As it can be seen (in the gray trace), the steady-state power values are: P1 = 309.53 W and P2 = 1190.5 W, confirming the (easily verifiable) theoretical optimal solution.

Source: Created by the authors.
Figure 8 Pseudocode for the Algorithm executing the Optimization Routine
Moreover, in Figure 9 a dynamic calculation for the total cost function C(P1, P2) is performed, activating the optimization algorithm at t = 0.24 s and being followed by an alteration in the cost function for the battery bank at t = 0.5 s.
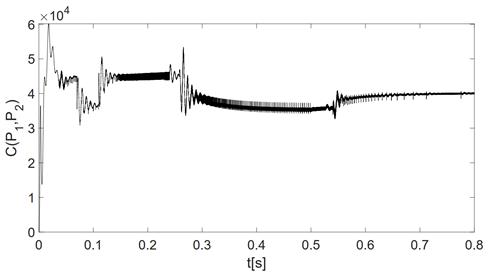
Source: Created by the authors.
Figure 9 Total cost function calculated with and without optimization
From those results, it is clear that after starting the optimization routine, the calculated total cost tends to be reduced. This fact is consistent with the expected behavior of minimization. Also, there is a small increment after changing the generation cost of the battery bank unveiling the self-adjustment capacity of the proposed approach to adapt energy management to dynamic rules, a situation needed in practice for the appropriate distribution of resources in a real microgrid.
5. CONCLUSIONS
A proposal to perform energy management in isolated DC microgrids employing renewable resources has been addressed. The approach consisted of a hierarchical structure based on droop control driving internal loops of PI classical controllers regulating the electrical variables of DC/DC boost power converters. In order to perform power-sharing and corresponding energy management, it is mandatory to achieve first the appropriate regulation at each generator. In accordance, Figure 3 has shown the dynamic improvement achieved by internal control loops compensating for undesired environmental variations in electrical variables of the system. From there, the controlled system has soft transients with fast recovery for desired reference values. Then, the power proportions can be selected attending to restrictions and cost functions to minimize (optimize) the operation of the microgrid system. For illustration, a simple algorithm based on the Newton-Raphson method was implemented and incorporated into numerical simulations of the grid, showing promising results by dynamic scheduling of power references adapted to environmental conditions. This was reflected in Figure 7 by the change in power trends at each generator, as well as by the reduction in the overall system cost along the time, as depicted in Figure 8.
From there, it is noticeable that despite the increase in generated power under perturbations, the total cost of the optimized mode is always below the cost calculated before activating the optimization algorithm. Ongoing work aims to verify the numerical results presented here but in a real laboratory prototype.






























