1. INTRODUCTION
Combustion of fossil fuels is still widely used around the globe for various services both at the industrial and residential levels. This chemical reaction emits pollutants that can have environmental impacts, such as NOx and CO2. Therefore, there is interest in developing next-generation combustion technologies, such as hydrogen-based combustion, and there is also a need for improving or retrofitting existing equipment [1]. MILD combustion [2], also known as colorless [3] or flameless combustion [4] is a promising technology for these purposes.
The concept of flameless combustion was first introduced by Wünning [4], [5]. This regime is achieved by preheating and diluting the fresh air-fuel mixture with hot flue gases. Significant dilution with these gases results in a reaction without a visible flame front and a uniform temperature distribution with low NOx emissions. The critical parameter for achieving flameless combustion is the recirculation factor Kv, defined as a ratio of recirculated mass flow to the input mass flow to the furnace [2]. In such studies, a flameless regime for methane was achieved with Kv values ranging from approximately 3 and 8, for furnace temperatures above the self-ignition temperature of the flammable mixture.
Cavaliere and de Joannon later formally defined MILD combustion regime [2], [6]. MILD is an acronym that refers to a “Moderate or Intense Low-oxygen Dilution” regime where two conditions must be satisfied: First, the reactive mixture must be above self-ignition temperature. Second, the temperature increases inside the furnace due to reaction (∆T) must be lower than the self-ignition temperature (T si ). This definition was obtained using a perfectly stirred reactor analysis. Flameless can be regarded as a practical way to obtain a MILD combustion regime, where strong dilution due to recirculation leads to a lower oxygen concentration in reactants and a lower temperature increase in the furnace. If the temperature of the reactive mixture is above self-ignition temperature, MILD conditions are satisfied.
Both definitions of flameless and MILD combustion are the subject of intense debate, suggesting that the underlying physics of this phenomenon is not yet completely understood [7]-[9]. The parameter Kv, which is used to characterize the recirculation intensity in MILD combustion, has several limitations as identified in literature. It can be easily calculated for an external gas recirculation (EGR) case if fuel, oxidizer, and recirculated gas mass flow rates are measured. However, in several furnaces, internal gas recirculation (IGR) is used, where high impulse jet flows create recirculating swirls. In such cases, measuring the aerodynamic Kv is challenging and it is usually estimated by CFD simulations [10].
For an IGR case, there are several Kv values inside the furnace due to the variation in mass flow being recirculated from point to point [10]. A common assumption is to report the maximum Kv value [8], [11] . Furthermore, Kv can also vary depending on whether the fuel and oxidizer flows are premixed or non-premixed before the reaction [7]. Despite its drawbacks, Kv is still a widely used parameter for studying flameless combustion.
This work aims to bridge the gap between MILD and flameless combustion definitions by proposing a parameter based on mass balance called recirculation ratio Z. With this parameter, the critical point for establishing the MILD combustion regime unconditionally is evaluated. This study includes numerical simulations of reactor networks considering CH4 and C2H6, and the calculation of reactor temperatures using an energy balance of C3H8 and H2. An algorithm for constructing combustion maps is presented, and the unconditional MILD critical point is identified and analyzed in connection to Kv, Z, and oxygen concentration.
2. METHODOLOGY
2.1 Reactor network
Figure 1 presents the reactor network that was simulated in this work. Initially, there is a premixer where fuel and oxidizer are combined at 300 K and 101.325 kPa. The oxidizer considered in this work is dry air, which is composed of 21 % O2 and 79 % N2 by volume. This study focuses on lean combustion mixtures with equivalence ratios (ϕ) ranging from 0.6 to 1. While the approach presented here can be extended to rich mixtures, this work focuses explicitly only on lean mixtures, as studies reported in the literature of MILD and flameless combustion often involve an excess of air [7], [8], [12]. The fuels simulated in this study are methane (CH4) and ethane (C2H6), and the reactive mechanisms used are GRI-Mech 3.0 [13] and Politecnico di Milano version C1-C3 NOx version 2003 published in 2020 (referred to as “Polimi” in the rest of the document) [14]- [17]. After the premixing stage, there is a mixer where the fresh fuel-air premixture is combined with hot flue gases before reacting inside an adiabatic perfectly stirred reactor (PSR). After the reactor, there is a splitter stage where a portion of the combustion gases is recirculated back to the mixer. This reactor network has been coded and simulated using the open-source software Cantera, version 2.5.0 [18].
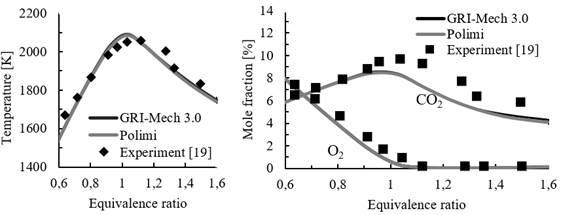
To validate the simulations of PSR carried out in Cantera, simulations with CH4 were conducted and compared with experiments reported in the literature [19], [20], as shown in Figure 2. The volume of the combustor was set to 2.5x10-4 m3, heat losses from the walls were assumed to be 100 W and residence time in the reactor was set to 0.086 s. These values are similar to those used in a previous numerical study [21]. Equivalence ratio ϕ was varied from 0.6 to 1.6.
Source: Created by the authors.
Figure. 2 Temperature of the reactor (left) and molar fraction of O2 and CO2 (right) at different equivalence ratios
The results obtained from the simulations show reasonable agreement with experiments for temperature and species, particularly for lean combustion mixtures (ϕ<1), as shown in Figure 2. Therefore, the simulation framework proposed in this work is considered acceptable. For all other simulation cases, adiabatic reactors are considered with a residence time of 1 s.
2.2 Algorithm of calculation
Table 1 presents the criteria for achieving MILD combustion adopted in this work. In general terms, MILD combustion is achieved if the reactive mixture is above self-ignition temperature (T si ) and temperature increase (∆T) due to the reaction being lower than T si .
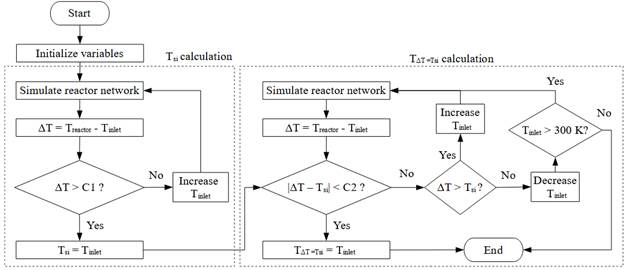
Therefore, the determination of MILD combustion conditions for a reactive mixture can be divided into two parts, as shown in Figure 3. First, T si is determined, and then ∆T is evaluated. Ignition of the mixture is achieved by increasing the inlet temperature (T inlet ) of the reactor up to the point where ∆T is above a constant C1, which in this work is set at 100 K. This ignition criterion is relatively simple to implement compared to more sophisticated approaches available in the literature [22]. However, it might have a shortcoming for MILD combustion when mixtures are significantly diluted, as ∆T could become lower than C1. Such mixtures with low oxygen concentration are further analyzed in the results based on the required recirculation ratios.
Source: Created by the authors.
Figure. 3 Algorithm for calculation of T si and T inlet where ∆T = Tsi
Once T si is determined, ∆T is calculated as the difference between reactor temperature and inlet temperature. In case ∆T is higher or lower than T si , the inlet temperature (T inlet ) is increased or decreased, respectively, and the reactor network is simulated again. The calculation continues until ∆T and T si are close to each other within a prescribed tolerance C2 (set to 1 K in this work), resulting in T inlet where ∆T = Tsi (in short, ∆T = T si ).
The second part of the algorithm (determination of T inlet where ∆T = Tsi ) was also calculated in this work using an energy balance in Cantera. This approach is faster as it determines the reactor temperature after calculating the enthalpy balance, rather than simulating a network of reactors. The procedure for this calculation is similar to the one used to determine the theoretical adiabatic temperature of a reactor with an initial reactor temperature equal to T si , which is well-documented in literature [23], [24]. In addition to methane (CH4) and ethane (C2H6), propane (C3H8) and hydrogen (H2) were also simulated using this faster approach.
2.3 Theoretical modeling
Consider the theoretical one-step lean combustion reaction for a hydrocarbon in the form C α H β with recirculation [23] in (1):
Where coefficients a, b, c, and d are respectively presented in (2):
Z is the recirculation ratio, which a dimensionless parameter that measures the amount of flue gases that are recirculated from products to reactants. An analysis of (2) brings two conclusions about Z: first, it cannot be equal to 1 because the denominators would be zero (Z = 1 would mean that all combustion gases are recirculated, which is impossible). And second, Z could not be higher than 1 or lower than 0 because it would cause negative species coefficients in the reaction. Therefore 0 ≤ Z < 1, where Z = 0 corresponds to no recirculation.
Mass balance [24] of the ideal reaction is (3):
Where m ̇ is mass flow and r, p and rec subscripts are reactants, products, and recirculated, respectively. Equation (3) can be restated as (4):
Where cg subscript means combustion gases. Recirculation factor Kv defined in literature is [4], (5):
Recirculated mass flow is a fraction of the total mass flow of combustion gases. Therefore, the formal definition of recirculation ratio Z is (6):
Where 0 ≤ Z < 1. Both Kv and Z can be calculated from each other as (7):
Two MILD combustion regimes can be classified based on the parameter Z. First, there is an unconditional MILD (UMC) regime if the reaction occurs at or above a critical recirculation ratio Z c at which any mixture capable of self-ignite will be MILD, which means that T inlet > T si, ∆T< T si and Z ≥Z c . And second, there is a conditional MILD (CMC) regime if Z is lower than Z c . This corresponds to a regime where T inlet > T si, ∆T< T si and Z < Z c . In both cases, the critical recirculation ratio Z c is defined as the Z where T inlet = T si and ∆T = T si .
3. RESULTS AND DISCUSSION
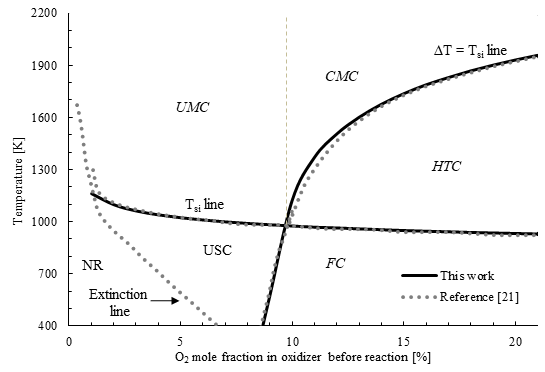
Figure 4 presents a map of MILD combustion regime for the case of CH4-air mixture at stoichiometric equivalence ratio (ϕ=1), simulated using the GRI-Mech 3.0 mechanism. The oxidizer in this simulation is synthetic air, which is a mixture of oxygen and nitrogen only. The results obtained in this work are consistent with previous results reported in the literature, which were performed using Chemkin-pro [21]. This work focuses on the critical point that results from the intersection of the T si line and the ∆T = T si line. For the CH4-air case at ϕ=1, this critical point is at an oxygen mole fraction of 9.7 %. This means that any reactive mixture with an oxygen mole fraction above 9.7 % and a temperature above T si will exhibit MILD combustion, and this zone is identified as UMC. It is worth noting that it is not necessary to reach such low oxygen levels for achieving MILD in this case, but simulations were performed up to an oxygen mole fraction of 1 % to investigate the behavior in extremely dilute conditions. Below this oxygen level, combustion becomes very difficult to establish, and the self-ignition line converges to the extinction line in Figure 4.
Source: Created by the authors.
Figure. 4 Combustion map in a PSR for a CH4-synthetic air mixture at different oxygen concentrations for an equivalence ratio of 1
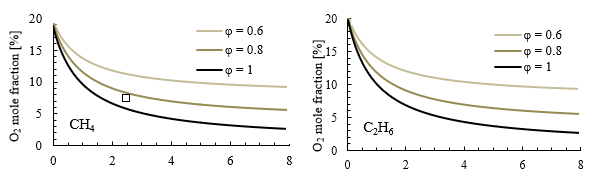
Figure 5 presents the oxygen mole fraction in the oxidizer as a function of the recirculation factor Kv for CH4 and C2H6 cases at three different equivalence ratios. These results consider flue gas recirculation obtained after simulating the reactor network, rather than using synthetic air. In all cases, an increase in recirculation factor Kv leads to dilution of the mixture, resulting in a decrease in the oxygen mole fraction before the reaction. This decrease in oxygen concentration is more pronounced at lower Kv values, between 0 and 2. Beyond Kv = 2, oxygen concentration still decreases with a less steep slope. The results also show that achieving extremely low oxygen levels, such as 1 %, would require a recirculation factor Kv higher than 8 at stoichiometric conditions for methane. This indicates that a significant amount of flue gas recirculation would be needed to achieve such low oxygen levels in the oxidizer for methane combustion.
Source: Created by the authors.
Figure. 5 Effect of recirculation factor on oxygen mole fraction for methane (left) and ethane (right) at different equivalence ratios
Achieving mixtures with very low oxygen concentrations through internal aerodynamic recirculation can be challenging, as pointed out in experiments reported in the literature [25].
Therefore, mixtures with deficient O2 concentrations (i.e., 1 %) would be only possible by the creation of synthetic air in a laboratory by mixing O2 and N2 at a fixed amount, instead of using actual recirculation of combustion gases for lean or stoichiometric equivalence ratios.
Figure 6 shows a comparison between two different combustion mechanisms, namely “GRI-Mech 3.0” and “Polimi”. The same map of MILD combustion regime presented in Figure 4 is redrawn with both mechanisms. Both mechanisms present similar results, although the critical point in the case of “Polimi” is higher, closer to 10 % oxygen. The “Polimi” mechanism is known to have updated kinetics and can be used for a broader range of fuels compared to GRI-Mech 3.0. However, GRI-Mech is used for simulations of all fuels considered in this work as it requires lower computational power compared to Polimi mechanism.
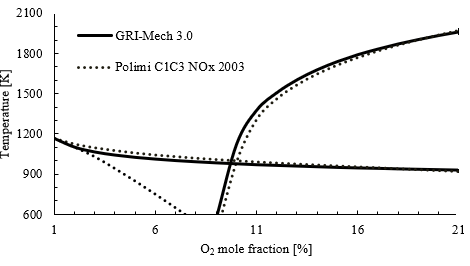
Source: Created by the authors.
Figure. 6 Combustion map in a PSR for a CH4 with synthetic air calculated with different combustion mechanisms for an equivalence ratio of 1
Figure 7 shows the map of MILD combustion constructed using two different approaches: synthetic air (discontinuous line) and recirculating flue gases (continuous line). Synthetic air, a mixture of O2 and N2, is commonly used as the oxidizer for building this kind of map [21]. This mixture assumes that all dilutants are nitrogen. However, when actual flue gas is recirculated, the composition of dilutants may also include other substances such as carbon dioxide (CO2) or water (H2O). When accounting for flue gas recirculation, the critical point for UMC shifts to a higher O2 mole fraction, in this case, to 10.6 %. Furthermore, the maximum mole fraction is no longer 21 % as in air, only about 18.9 %, because even when there is no recirculation (Kv = 0), air is premixed and diluted with fuel. Therefore, caution must be exercised when comparing critical points from different combustion maps, as not all maps are constructed in the same way, and the oxygen fractions may be either from oxidizer (as in synthetic air maps) or from flue gas/fuel/air mixture before reaction (as proposed in this study).
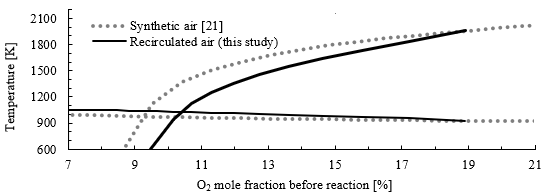
Source: Created by the authors.
Figure. 7 Combustion map in a PSR for a CH4 with synthetic air compared with recirculated air for an equivalence ratio of 1
Figure 8 presents combustion maps for CH4 and C2H6 at three different equivalence ratios: 1, 0.8 and 0.6. For both fuels, the critical point changes significantly: in the case of methane, it shifts from 10.6 % at ϕ=1 to about 15.5 % at ϕ=6.0, which is consistent with previous studies [21]. However, an interesting observation that has not been reported before is the critical recirculation factor Kv that corresponds to each case. For CH4, it decreases from Kv = 0.86 at ϕ=1 to Kv = 0.59 at ϕ=0.6. This implies that as the equivalence ratio decreases, the requirements for mass recirculation also decrease. In other words, it becomes easier to establish MILD combustion by recirculation at leaner equivalence ratios.
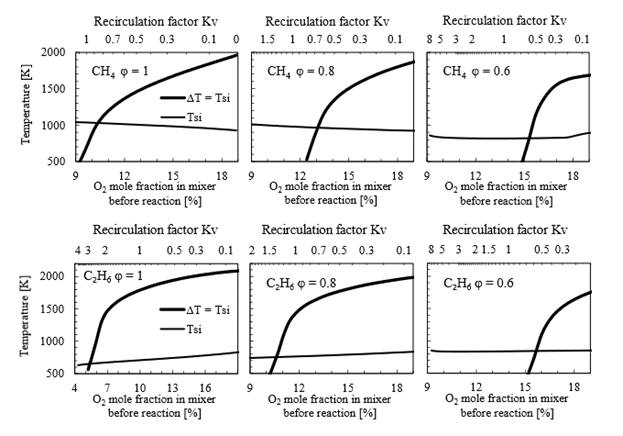
Source: Created by the authors.
Figure. 8 Combustion map in a PSR for a CH4 (above) and C2H6 (below) with recirculated flue gases for an equivalence ratio of 1 (left), 0.8 (center) and 0.9 (right)
In the case of C2H6, critical Kv is significantly higher compared to CH4. For example, at ϕ=1, critical Kv for ethane is more than three times what is required for methane. This demonstrates that the critical Kv or O2 level for UMC is dependent on both fuel type and equivalence ratio and can vary considerably.
It is also noteworthy that the self-ignition temperature changes with oxygen mole fraction and may either increase or decrease with Kv. However, at ϕ=0.6 for both fuels, it becomes almost horizontal, meaning that T si does not change significantly with oxygen concentration. This implies that under such conditions, UMC can be achieved for a wide range of recirculation factors. In the lean equivalence ratio, which involves an excess of air, this excess aids in diluting the mixture effectively while maintaining sufficient oxygen for the reaction to initiate and sustain.
Figure 9 shows the relationship between recirculation ratio Z and recirculation factor Kv, which was determined through numerical analysis. It is observed that this relationship does not change with fuel or equivalence ratio. A recirculation ratio Z of 0.5 signifies that half of the combustion gases are being recirculated back into the reactor, corresponding to Kv = 1. However, as Kv further increases, Z increases slowly, suggesting that Z converges to unity for an infinite Kv. In practical applications, achieving a Kv value higher than eight through aerodynamic recirculation is challenging [25].
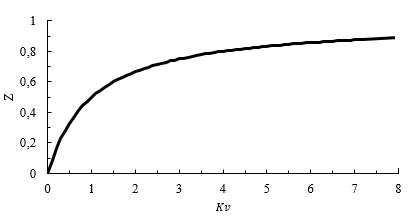
Source: Created by the authors.
Figure. 9 Recirculation ratio Z as a function of recirculation factor Kv
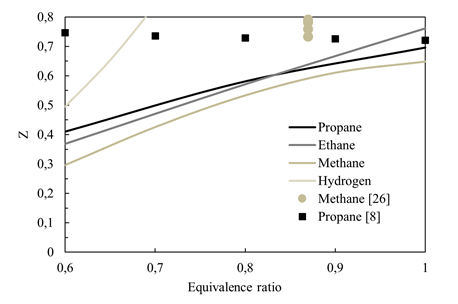
Figure 10 presents the critical recirculation ratio Z c as a function of fuel and equivalence ratio. Across all fuels, the trend is consistent: as the equivalence ratio increases, a higher recirculation ratio is necessary. Notably, among the fuels simulated, methane requires the lowest Z c , while hydrogen necessitates the highest Z c . This observation is noteworthy as hydrogen combustion does not produce carbon dioxide as the other fuels investigated.
Source: Created by the authors.
Figure. 10 Critical recirculation ratio Z c as a function of fuel and equivalence ratio
For alkanes such as CH4, C2H6 and C3H8, the maximum ∆Z c for any given, lean equivalence ratio is only 0.1. This indicates that the requirements for achieving unconditional MILD combustion, as measured by Z c , are similar among these fuels. However, for H2, due to the lack of CO2 production during combustion, it becomes challenging to achieve unconditional MILD combustion for equivalence ratios above 0.7 as it would require a significantly large Z c (and Kv as well). This provides a theoretical basis for diluting pure hydrogen combustion with CO2 to reduce the requirements of internal gas recirculation for achieving UMC at virtually any lean equivalence ratio considered in this work. Furthermore, Figure 10 includes data points from previous literature for MILD combustion experiments with methane [26] and propane [8]. The results presented in Figure 10 agree with the findings from these previous studies, as Z is higher than the theoretical Z c calculated in this work for both methane and propane cases.
4. CONCLUSIONS
This work analyzed the conditions for establishing the unconditional MILD combustion regime under flue gas recirculation, using numerical simulations for lean combustion of CH4, C2H6, C3H8, and H2. The critical point that marks the start of such regime can be identified by the self-ignition temperature and a particular oxygen concentration in the mixture before the reaction. This point changes significantly from fuel to fuel and depends on the global equivalence ratio.
A parameter called recirculation ratio Z was introduced based on mass balance. According to the results, Z better captures the critical recirculation requirements of UMC regime compared to the standard recirculation factor Kv, for most of the fuels considered within a Z c = 0.1 for any of the lean equivalence ratios studied.
In all cases studied, the critical ratio Z c diminishes with the equivalence ratio. Methane requires the lowest Z c while hydrogen requires the highest. In fact, for H2, unconditional MILD combustion could only be obtained for equivalence ratios below 0.7 and at Z c between 0.5 and 0.8. H2 does not have CO2 as a dilutant in flue gases compared to the other fuels studied; therefore, this result suggests that performing dilution with CO2 could reduce recirculation requirements for MILD combustion of pure hydrogen.
Further work could focus on the extension of the analysis to other fuels and conditions such as investigation of the effect of different dilutants on recirculation requirements for unconditional MILD combustion.
























