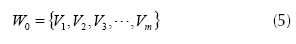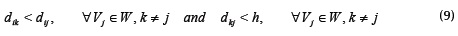Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Tecnura
Print version ISSN 0123-921X
Tecnura vol.20 no.47 Bogotá Jan./Mar. 2016
https://doi.org/10.14483/udistrital.jour.tecnura.2016.1.a02
DOI: http://dx.doi.org/10.14483/udistrital.jour.tecnura.2016.1.a02
Collective Multi-Agent Navigation Model Based on Bacterial Quorum Sensing
Modelo de navegación colectiva multi-agente basado en el Quorum Sensing bacterial
Edwar Jacinto Gómez1, Mauricio Giral2, Fredy Hernán Martínez Sarmiento3
1 Electronic Control and Instrumentation Engineer, Sciences of the Information and Communications Master, Professor at the District University Francisco José de Caldas, Bogotá D.C., Colombia. Contact: ejacintog@udistrital.edu.co
2 Electronic Control and Instrumentation Engineer, Bioengineering Specialist, Electronic Engineer Student Master University Santo Tomas, Bogotá D.C., Colombia. Contact: wimagira@gmail.com
3 Electrical Engineer, Engineering Project Management Specialist, Systems and Computer Engineering Ph.D.(c), Professor at the District University Francisco José de Caldas, Bogotá D.C., Colombia. Contact: fhmartinezs@udistrital.edu.co
Fecha de recepción: 14 octubre de 2014 Fecha de aceptación: 18 de septiembre de 2015
Cómo citar: Jacinto, E., Giral, M., & Martínez, F. (2016). Collective multi-agent navigation model based on bacterial Quorum Sensing. Revista Tecnura, 20(47), 29-38. doi: 10.14483/udistrital.jour.tecnura.2016.1.a02
Abstract
We present a model for the study, analysis, design and evaluation of collective multi-agent navigation for autonomous robots based on behaviors observed in bacteria. The system consists of a set of simple agents (artificial bacteria), which through readings and local interaction are self-organized to navigate along the environment. Given the parallel structure, also happens to be a very robust solution. We show the basic structure proposal for the design abstracting the characteristics of the biological model, together with an analysis of stability and convergence.
Keywords: collective navigation, intensity gradient, quorum sensing.
Resumen
Se presenta un modelo para el estudio, análisis, diseño y evaluación de navegación colectiva multi-agente para robots autónomos basado en comportamientos observados en bacterias. El sistema consiste de un conjunto de agentes sencillos (bacterias artificiales), los cuales a través de lecturas e interacciones locales se auto-organizan para navegar a lo largo del ambiente. Dada la estructura paralela, también resulta ser una solución muy robusta. Se muestra la estructura básica propuesta para el diseño abstrayendo las características del modelo biológico, en conjunto con un análisis de estabilidad y convergencia.
Palabras clave: navegación colectiva, gradiente de intensidad, quorum sensing.
Introduction
The problem of finding a robotic navigation path refers to make an agent (an object with physical dimensions) to move from one point (current configuration) to another point (desired configuration) in a navigation environment, avoiding obstacles with a minimum margin. This is currently an unsolved problem in robotics, and in fact, one of the most active fields worldwide.
The exact definition of a path for a real application is a computationally intractable problem (Idsardi, 2006). It is possible to significantly simplify the problem using geometric algorithms on the environment, such is the case of Voronoi diagrams (Xia y Xiangmin, 2014), (Kuo-Ho, Tan-Phat, Chan-Yun, y Wen-June, 2014), (Wei-Che, Chan-Yun, Kuo-Ho, y Yi-Hong, 2014), (Unghui, Sangyol, HyunChul, Vasseur, y Demonceaux, 2014), the A* search algorithm (Haifeng, Jiawei, Guifeng, y Yun, 2014), and in general, cells space decomposition algorithms (Holman, Jacinto, y Martínez, 2015), (Jan, Chi-Chia, Wei, y Ting-Hsiang, 2014), (Goyal y Nagla, 2014), (Delgado, Casallas, y Jacinto, 2014). However, these strategies can only produce useful results in real applications when the navigation environment is static, that is, it remains unchanged over a considerable period of time. This condition, in particular, is not satisfied where there are more than one agent.
Some more efficient algorithms as potential fields have serious problems of convergence and local minima (Amorim y Ventura, 2014), (Mohammadi, Rahimi, y Suratgar, 2014), (Li y Wei, 2014), which it is a big issue in a real application. One of the most efficient and robust strategies today to real problems of navigation in dynamic environments are algorithms based on local readings, formally known as Sampling Based Algorithms SBA (Van-Dung, Dongwook, Kurnianggoro, y Kang-Hyun, 2014), (Lianhang et al., 2014), (Narayanan, Vernaza, Likhachev, y LaValle, 2013). In contrast to the above mentioned methods, in which an explicit representation of the obstacles is performed in the configuration space (a configuration that describes the position of the robot, and the configuration space C, in the set of all possible configurations (LaValle, 2006)), representation that is used to build the solution, and hence the high computational cost, in the SBA it is primarily relies on a local sensing hardware aboard the agent, which provides information on possible navigation paths. This allows working with minimum and sufficient information to define the robot motion, reducing the computational load, while answers in real time allowing changes in the environment.
Under the SBA scheme, collecting and processing information is essential to the process of mapping the environment, location in the environment and path planning. The current configuration is estimated at the stage of location by sensing the configuration space (C-space), and scheduler allows to define the desired final configuration. By its nature, the sensing process is itself a random approach which has advantages in terms of being able to provide quick solutions to complex problems, but it has the disadvantage that such solutions are often suboptimal. There is no guarantee of finding an optimal navigation solution (in those cases that this exists), SBA algorithms are able to provide a solution, if there is a solution to the problem, provided there is sufficient time for the development of the algorithm (are unbounded in time). Therefore, these schemes guarantee its success (completeness) under the concept of probabilistic completeness (it is not possible to define explicitly the time required to find the solution, but if there is a solution, the algorithm will find it).
We propose a scheme of collective bio-inspired navigation based on self-organization. Self-organization has been the subject of great theoretical research, however, its practical application in solving actual problems on the contrary has not been very noticeable, or with impact (Prokopenko, 2008). Some attempts that have been documented in this respect are the works of Mange (Mange et al., 1996), (Freitas y Gilbreath, 1980), where they document some developments on FPGAs in bio-inspired hardware that somehow involve cellular reconstruction models, replicating them to build robust applications, systems resilience to physical damage. Such developments involve two importances biological processes at the cellular level: replication and regeneration. These two processes are crucial in any bio-inspired model that tries to replicate structures at the cellular level, such as the bacterial Quorum Sensing (QS), biological model used as reference in this research.
This paper is supported on various works related to research focused on growth and development of bacteria, both from the biological point of view and the point of view of engineering (Karafyllidis, 2011), (Wiedermann, 2011), (Besozzi, Cazzaniga, Mauri, y Pescini, 2011), (Shen y Zhou, 2010), (Niu, Fan, Tan, Rao, y Li, 2010), (Taylor, Tinsley, Wang, Huang, y Showalter, 2009). From the latter field, a lot of research is seen in search and optimization processes, specifically in computational intelligence, where the growth, development and interaction between bacteria offers interesting behavioral models (Zang, He, y Ye, 2010), (Cho y Kim, 2011), (Gómez y Rodríguez, 2011), (Goni, Redondo, Arroyo, y Castellanos, 2011), (Connelly y McKinley, 2011). In particular, it comes to have a structure capable of modeling individuals, groups of individuals, and their communication processes (Martínez y Delgado, 2010).
The paper is organized as follows. In Section 2 problem formulation is discussed, Section 3 describes the control strategy. Finally, conclusion and discussion are presented in Section 4.
PROBLEM FORMULATION
Let W  R2 be the closure of a contractible open set in the plane that has a connected open interior with obstacles that represent inaccessible regions (Gonzalez, Ghaffarkhah, y Mostofi, 2014). Let O be a set of obstacles, in which each O
R2 be the closure of a contractible open set in the plane that has a connected open interior with obstacles that represent inaccessible regions (Gonzalez, Ghaffarkhah, y Mostofi, 2014). Let O be a set of obstacles, in which each O  O is closed with a connected piecewise-analytic boundary that is finite in length. Furthermore, the obstacles in O are pairwise-disjoint and countably finite in number. Let E
O is closed with a connected piecewise-analytic boundary that is finite in length. Furthermore, the obstacles in O are pairwise-disjoint and countably finite in number. Let E W be the free space in the environment, which is the open subset of W with the obstacles removed.
W be the free space in the environment, which is the open subset of W with the obstacles removed.
Let us assume a set of n agents in this free space. The agents know the environment E in which they move from observations, using sensors. These observations allow them to build an information space I. A information mapping is of the form of the equation (1).
where S denote an observation space, constructed from sensor readings over time, i.e., through an observation history of the form of the equation (2).
The interpretation of this information space, i.e.,  , is that which allows the agent to make decisions (LaValle, 2006).
, is that which allows the agent to make decisions (LaValle, 2006).
We assume the agents are able to sense the proximity of their team-mates and/or obstacles within the environment, using minimal information. The environment E is unknown to the robot. Furthermore, the robot does not even know its own position and orientation. Our goal is to design the control rules for the n robots in order to independently solve navigation tasks in a dynamic and unknown environment.
The particular equations of motion x=ƒ(x) for each robot is unimportant in this approach. We do not explicitly control their motions and do not even attempt to measure their precise state. Instead, we rely on the fact that the robot moves in a uncontrollable way, but the trajectory satisfies the following high-level property: For any region r ∈ R it is assumed that the robot moves on a trajectory that causes it to strike every open interval in ∂r (the boundary of r) infinitely often, with non-zero, non-tangential velocities.
However, the robots should not move randomly in the environment, they should jointly develop a task. To achieve this, we propose a design model based on the collective behavior of robots. This collective behavior involves a local interaction at agent level, reflecting a system-level behavior. These behaviors in conjunction with some control modes encoded in all agents, enable the coordinated navigation of the robots.
We develop an event-based system. Each robot starts with an initial control mode. During execution, the control mode may change only when receiving an sensor observation event y. Let Y denote the set of all possible observation events for a robot in a particular system, then y ∈Y. The control modes of robot i are set during execution according to a policy. Since state feedback is not possible, information feedback is instead used. A control policy is specified as an information-feedback mapping which enables the control mode to be set according to the sensor observation history.
Methodology
The multi-agent model proposed is composed of a set of artificial bacteria or agents. This set of agents, and their interactions, reflect the dynamics that will navigate. All agents are identical in design. Nevertheless, to solve tasks, each of them undergoes certain behavior inside the system along the time.
The variables of this system are defined in a continuous space. However, the different agent behaviors are triggered by certain events (event-based), which implies that the appropriate analysis model is a hybrid system (the dynamic changes from one state to another when a condition is present).
Multi-agent dynamic system
The multi-agent model adopted for collective path planning is composed of a set of artificial bacteria or agents. This set of agents, and their interactions, reflect the navigation dynamics. All agents are identical in design. Nevertheless, each of them undergoes certain behavior inside the system along the time.
The variables of this system are defined in a continuous space. However, the different agent behaviors are triggered by certain events (event-based), which implies that the appropriate analysis model is a hybrid system (the dynamic changes from one state to another when a condition is present).
The simplified model of bacterial QS describes a set of independent cells, which under the generation of extra-cellular signals produce coordinated social behaviors (Otero, Munoz, Bernández, y Fábregas, 2004). The pathogenic bacteria that carry multicellular organisms are not virulent until they reach a sufficient majority to enforce a massive attack against the immune system. When bacteria determine that their population size is enough to trigger an attack, they transform and become virulent.
Definition 1. A bacterium is a pair (equation (3)).
where ƒ is a nonnegative integer  that indicates the amount of neighboring bacteria in direct contact, and p is a point in q-dimensional space
that indicates the amount of neighboring bacteria in direct contact, and p is a point in q-dimensional space  (Martínez S. y Delgado, 2010).
(Martínez S. y Delgado, 2010).
The bacterial recognition occurs in a bacterium Vi when the bacterium defines its values ƒ and P. This definition corresponds to an extension of the cell definition in the antibody-antigen mathematical model (Tarakanov y Dasgupata, 2000).
Definition 2. The population density is evaluated using the distance between bacteria (equation (4)).
as the distance between bacteria Vi and Vj, which is calculated by any appropriate norm.
Definition 3. A bacterial population is defined as a nonempty set of bacteria (equation (5)).
with non-zero distance among bacteria (equation (6)).
The bacteria that implement the navigation task are called here Application Bacteria, AB, and are a subset of the bacterial population (figure 1).
That is, W0 is the set of all bacteria in the system, and W is the set of virulent bacteria in the system.
Definition 4. The neighborhood threshold h, indicates the maximum amount of direct neighboring bacteria that a cell can have.
Throughout reproduction, the population size (number of agents) is always compared to T, the quorum threshold, it is the parameter defining whether or not it has reached the quorum. Regarding the physical dimensions of the bacterial population, the density threshold h indicates the minimum distance needed between bacteria; in other words, the minimum distance that must exist between any pair of bacteria.
The behaviors of bacteria (self-organization) are coordinated by the following rules (the model does not include cell death):
Reproduction Rule: If the bacterium  can reproduce (equation (8)).
can reproduce (equation (8)).
then Vi must reproduce by duplicating their DNA (code) in the available medium.
In other words, if the bacterial population is very small and the non-virulent bacterium Vi can reproduce, then Vi must reproduce (must copy its code to a neighboring inactive).
Virulence, Activation or Cell Differentiation Rule: If the bacterium Vk ∈W is the nearest to the bacterium  among all AB (figure 1).
among all AB (figure 1).
and the number of bacteria in W is less than T, then Vi must be added to AB (the bacterium becomes virulent).
In other words, if the AB is very small and the non-virulent bacterium Vi is the nearest to a virulent bacterium, then Vi must become virulent (must solve the task with the other bacteria of AB).
Stability, convergence and parameters selection
The stability and convergence of the model is dependent on the parameters selected for the design of the navigation environment. Because the schema is supported in local readings, its use in real applications requires modification (design) of the navigation environment. The parameters selection is essential for this design and modification of the environment.
The design of the navigation environment consists of defining the areas of E to be the final destination for the agents, and then place in them and in their neighborhoods, special marks (landmarks) that indicate this condition. Generally these landmarks are not equal, each value indicates the intensity corresponding to its position in E. The intensity value is designed for the entire navigation environment, so it grows near the final destination area.
Thus, during the search process (navigation), agents interpret local readings and determine the intensity value at each point of the environment. Climbing the slope of these values, each agent follows a heuristic that allows it to choose the optimal choice in each advance as does a greedy algorithm. Although such an approach can be inappropriate for some computational tasks (the strategy stagnates in local solutions without finding the global optimal solution), for the proposed algorithm based on QS this constitutes an exploration strategy that ultimately ensures convergence in the global optimal solution.
The effect of QS on the population is to accelerate the convergence in the areas of high performance. For this, the model takes into account the population size in the area, increasing the attraction when a threshold is exceeded. The value of the slope is designed as a function of the density threshold.
The following sections will show how to model the navigation field intensity as a gradient on the environment. This section focuses only in the vicinity of an area of high performance (area to be interpreted by the agents as of interest), and how to design a simple intensity field according to a slope, considering the issues of convergence.
The gradient in the area can be modeled by a system of two autonomous first-order ODEs (Ordinary Differential Equations), model in which the slope at each point represents the intensity of the gradient. To plot the slope field, the two autonomous ODEs must be written in the form (equation (10)).
That is, the first expression is the derivative of the variable represented on the horizontal axis of the environment, and the second expression is the derivative of the variable represented on the vertical axis of the environment. The origin corresponds to the center of the area of high performance.
The two functions must confine the agents at the origin. Since the slope of the two curves are who push the agents, it is possible to think of a curve design for x and y as shown in figure 2.

These two curves are designed in such a way that with their growth there is no possibility of way between them. Curve y (green) is a reflection of the curve x (blue), and the slopes push towards the origin. To facilitate the calculation of derivatives, these curves can be replaced by exponential approximations (equation (11)).
In these two curves is easy to define the behavior: α is the reference value and t is the time constant, which directly affects the slope of the curve, and can be defined as a function of the density threshold.
To represent graphically the slope field is necessary to calculate the derivatives of the curves (equation (12)).
Since these curves are exponential, we subtract to each one the value of the other variable to prevent grow up indefinitely (y to x and x to y). The figure 2 shows the slope field for a time constant of:  .
.
The figure 4 shows the x and y curves for the resulting motion curve shown in figure 3 (red curve).
From the model and these behaviors is possible to conclude some general characteristics in terms of stability and convergence.
Lemma 1: Let 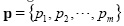 be a set of points drawn randomly in E on a two-dimensional Euclidean plane R2, each with an associated slope value m according to some law of navigation. Let G(x,y) be a function on R2 that assigns a slope value to each point p ∈ p, such that the maximum value is assigned to the central point of the area of high performance. Then there exists a point p0/ such that
be a set of points drawn randomly in E on a two-dimensional Euclidean plane R2, each with an associated slope value m according to some law of navigation. Let G(x,y) be a function on R2 that assigns a slope value to each point p ∈ p, such that the maximum value is assigned to the central point of the area of high performance. Then there exists a point p0/ such that  , where P0 is the closest point to the center of the area of high performance.
, where P0 is the closest point to the center of the area of high performance.
Proof: By construction the maximum value of m is assigned to the central point of the area of high performance. If this construction is correct, P0 always exists. p0 is the p ∈ p closest point to the area of high performance. Furthermore, since the heuristic climbs always looking for the right next value, the agent eventually will find this point p0 if there are no other areas of high performance.
Lemma 2: If there is at least one area solution in E, incorporation of QS in finding solutions does not produce stability problems in the search algorithm. By contrast, this reduces the convergence time.
Proof: The proposed algorithm based on QS alters the behavior of the function G(x,y) at points near to the high performance area. This alteration is conditioned to the density threshold, producing localized alterations if the population in the area exceeds that threshold. QS increases the weight of the solution, and therefore reducing the total search time. However, QS does not change the global behavior of G(x,y), therefore does not affect the convergence of the search.
Conclusions
In this paper we propose a model for collective multi-agent navigation that enables the analysis and design of navigation tasks for an autonomous group of robots. The model is inspired by bacterial interaction, and describes a simplified behavior of bacterial QS, which serves to define an artificial bacterium, its characteristics of interaction, and its basic navigation conditions. The structure assumed in the proposed model is hybrid, in which behaviors that can be analyzed continuously are triggered by events (local readings) characterizing discrete transition. Taking as a design strategy landmarks allocation based on density gradients, we demonstrated that the system is stable and converges to a solution if it exists. Thus, we show how a group of robots can be used to solve simple navigation tasks without requiring system identification, geometric map building, localization, or state estimation, using a simple minimalist design in hardware, software and algorithm operation. The interaction between the robots responds to the simplified algorithm of local communication, which guarantees a minimum sensing, what makes the strategy promissory for exploration in collapsed and unknown environments. The capabilities and system functions can be scaled changing the number of robots.
Financing
This work was supported by the District University Francisco José de Caldas, in part through CIDC, and partly by the Technological Faculty. The views expressed in this paper are not necessarily endorsed by District University. The authors thank the research groups DIGITI and ARMOS for the evaluation carried out on prototypes of ideas and strategies.
References
Amorim, D., y Ventura, R. (2014). Towards efficient path planning of a mobile robot on rough terrain. En 2014 ieee international conference on autonomous robot systems and competitions (icarsc) (p. 22-27). [ Links ]
Besozzi, D., Cazzaniga, P., Mauri, G., y Pescini, D. (2011). Biosimware: A software for the modeling, simulation and analysis of biological systems. En M. Gheorghe, T. Hinze, G. Paun, G. Rozenberg, y A. Salomaa (Eds.), Membrane computing (Vol. 6501, p. 119-143). Springer Berlin Heidelberg. [ Links ]
Cho, J. H., y Kim, D. H. (2011). Intelligent feature selection by bacterial foraging algorithm and information theory. En Advanced communication and networking (Vol. 199, p. 238-244). Springer Berlin Heidelberg. [ Links ]
Connelly, B., y McKinley, P. (2011). Evolving social behavior in adverse environments. En G. Kampis, I. Karsai, y E. Szathmáry (Eds.), Advances in artificial life. Darwin meets von neumann (Vol. 5777, p. 490-498). Springer Berlin Heidelberg. [ Links ]
Delgado, G. I., Casallas, R., y Jacinto, G. E. (2014). Path planning in static scenarios using image processing and cell decomposition. En 2014 ieee international autumn meeting on power, electronics and computing (ropec) (p. 1-5). [ Links ]
Freitas, R., y Gilbreath, W. (1980). Chapter 5: Replicating systems concepts: Self-replicating lunar factory and demostration. En Advanced automation for space missions, 1980 nasa/asee summer study. [ Links ]
Gómez, P., y Rodríguez, A. (2011). Simulating a rock-scissors-paper bacterial game with a discrete cellular automaton. En New challenges on bioinspired applications (Vol. 6687, p. 363-370). Springer Berlin Heidelberg. [ Links ]
Goni, A., Redondo, M., Arroyo, F., y Castellanos, J. (2011). Biocircuit design through engineering bacterial logic gates. Natural Computing, 10, 119-127. [ Links ]
Gonzalez, A., Ghaffarkhah, A., y Mostofi, Y. (2014). An integrated framework for obstacle mapping with see-through capabilities using laser and wireless channel measurements. IEEE Sensors Journal, 14(1), 25-38. [ Links ]
Goyal, J., y Nagla, K. (2014). A new approach of path planning for mobile robots. En 2014 international conference on advances in computing, communications and informatics icacci (p. 863-867). [ Links ]
Haifeng, W., Jiawei, Z., Guifeng, Z., y Yun, L. (2014). Has: Hierarchical a-star algorithm for big map navigation in special areas. En 2014 5th international conference on digital home (icdh) (p. 222-225). [ Links ]
Holman, M., Jacinto, E., y Martínez, F. (2015). Generación de ruta óptima para robots móviles a partir de segmentación de imágenes. Información Tecnológica, 26(2), 145-152. [ Links ]
Idsardi, W. (2006). A simple proof that optimality theory is computationally intractable. Linguistic Inquiry, 37(2), 271-275. (The MIT Press). [ Links ]
Jan, G. E., Chi-Chia, S., Wei, C., y Ting-Hsiang, L. (2014). An shortest path algorithm based on Delaunay triangulation. IEEE/ASME Transactions on Mechatronics, 19(2), 660-666. [ Links ]
Karafyllidis, I. G. (2011). Regulating the quorum sensing signalling circuit to control bacterial virulence: in silico analysis. IET Systems Biology, 5(2), 103-109. [ Links ]
Kuo-Ho, T., Tan-Phat, P., Chan-Yun, Y., y Wen-June, W. (2014). Image-based smooth path planning for wheeled robot. En 11th ieee international conference on control and automation (icca) (p. 203-207). [ Links ]
LaValle, S. M. (2006). Planning algorithms (1.a ed.). Cambridge University Press. Retrieved from http://planning.cs.uiuc.edu/. [ Links ]
Li, C., y Wei, L. (2014). Adaptive artificial potential field approach for obstacle avoidance path planning. En 2014 seventh international symposium on computational intelligence and design (iscid) (Vol. 2, p. 429-432). [ Links ]
Lianhang, S., Min, L., Yang, L., Qing-Ying, Z., Jie, L., y Zhongya, W. (2014). A novel artificial bee colony optimization algorithm for global path planning of multi-robot systems. En 2014 ieee international conference on robotics and biomimetics (robio) (p. 1186-1191). [ Links ]
Mange, D., Goeke, M., Madon, D., Stauer, A., Tempesti, G., y Durand, S. (1996). Embryonics: A new family of coarse-grained field programmable gate array with self-repair and self-reproducing properties. LNCS Towards Evolvable Hardware, 1062, 197-220. [ Links ]
Martínez S., F. H., y Delgado, J. (2010). Hardware emulation of bacterial quorum sensing. En D.-S. Huang, Z. Zhao, V. Bevilacqua, y J. Figueroa (Eds.), Lecture notes in computer science 6215. Advanced intelligent computing theories and applications (Vol. 6215, p. 329-336). Springer Berlin Heidelberg. [ Links ]
Martínez, F., y Delgado, J. (2010). Hardware emulation of bacterial quorum sensing. Advanced Intelligent Computing Theories and Applications, LNCS 6215, 329-336. [ Links ]
Mohammadi, A., Rahimi, M., y Suratgar, A. (2014). A new path planning and obstacle avoidance algorithm in dynamic environment. En 2014 22nd iranian conference on electrical engineering (icee) (p. 1301-1306). [ Links ]
Narayanan, V., Vernaza, P., Likhachev, M., y LaValle, S. M. (2013). Planning under topological constraints using beam-graphs. En 2013 ieee international conference on robotics and automation (icra) (p. 431-437). [ Links ]
Niu, B., Fan, Y., Tan, L., Rao, J., y Li, L. (2010). A review of bacterial foraging optimization part i: Background and development. En Advanced intelligent computing theories and applications (Vol. 93, p. 535-543). Springer Berlin Heidelberg. [ Links ]
Otero, A. M., Munoz, A., Bernández, M. I., y Fábregas, J. (2004). Quorum sensing el lenguaje de las bacterias (First Edition ed.). Spain: Acribia. (ISBN 9788420010465. [ Links ])
Prokopenko, M. (2008). Advances in applied self-organizing systems. Springer Berlin Heidelberg. [ Links ]
Shen, J., y Zhou, H. (2010). The dynamics of quorum sensing mediated by small rnas in vibrio harveyi. En Life system modeling and intelligent computing (Vol. 97, p. 177-184). Springer Berlin Heidelberg. [ Links ]
Tarakanov, A. O., y Dasgupata, D. (2000, Feb.). A formal model of an artificial immune system. Biosystems, 55(3), 151-158. (ISSN 0303-2647). [ Links ]
Taylor, A. F., Tinsley, M. R., Wang, F., Huang, Z., y Showalter, K. (2009). Dynamical quorum sensing and synchronization in large populations of chemical oscillators. Science, 323(5914), 614-617. [ Links ]
Unghui, L., Sangyol, Y., HyunChul, S., Vasseur, P., y Demonceaux, C. (2014). Local path planning in a complex environment for self-driving car. En 2014 ieee 4th annual international conference on cyber technology in automation, control, and intelligent systems (cyber) (p. 445-450). [ Links ]
Van-Dung, H., Dongwook, S., Kurnianggoro, L., y Kang-Hyun, J. (2014). Path planning and global trajectory tracking control assistance to autonomous vehicle. En 2014 11th international conference on ubiquitous robots and ambient intelligence (urai) (p. 646-650). [ Links ]
Wei-Che, Y., Chan-Yun, Y., Kuo-Ho, S., y Yi-Hong, T. (2014). Dynamic path planning under randomly distributed obstacle environment. En 2014 cacs international automatic control conference (cacs) (p. 138-143). [ Links ]
Wiedermann, J. (2011). Nanomachine computing by quorum sensing. En J. Kelemen y A. Kelemenova (Eds.), Computation, cooperation, and life (Vol. 6610, p. 203-215). Springer Berlin Heidelberg. [ Links ]
Xia, C., y Xiangmin, C. (2014). The uav dynamic path planning algorithm research based on voronoi diagram. En The 26th chinese control and decision conference (2014 ccdc) (p. 1069-1071). [ Links ]
Zang, T., He, Z., y Ye, D. (2010). Bacterial foraging optimization algorithm with particle swarm optimization strategy for distribution network reconfiguration. En Advances in swarm intelligence (Vol. 6145, p. 365-372). Springer Berlin Heidelberg. [ Links ]