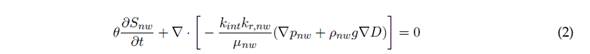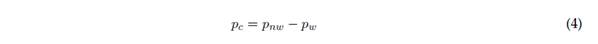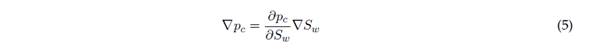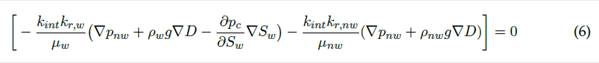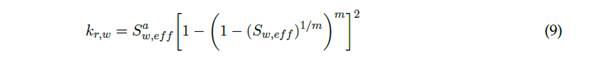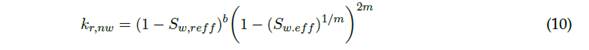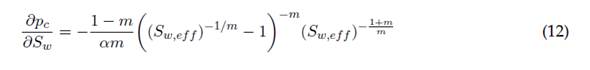INTRODUCCIÓN
La mayoría de las técnicas de mejoramiento de suelos susceptibles a licuefacción requieren un gran gasto energético debido a los procesos de producción y de construcción in situ. Existe una clara necesidad de desarrollar técnicas de mitigación de licuefacción rentables y aplicables sobre estructuras nuevas y existentes (Gallagher, Pamuk y Abdoun, 2007), por lo que científicos plantean la inducción parcial del grado de saturación como una de ellas (Okamura, Ishihara y Tamura, 2003). Este proceso radica en la introducción de burbujas de gas en el suelo, que provocan una disminución del módulo volumétrico y un aumento de la compresibilidad de la mezcla aire y agua dentro de los poros, de modo que cuando el suelo está sujeto a cargas cíclicas, el gas absorbe el exceso de presión de poros reduciendo su volumen (Okamura y Soga, 2006), lo que resulta en un aumento de la resistencia a la licuefacción. Algunos métodos propuestos para generar burbujas son la inyección de aire (Ishihara, Okamura y Oshita, 2003), la electrólisis del agua (Yegian, Eseller-Bayat, Alshawabkeh y Ali, 2007), las reacciones químicas (Eseller-bayat, Yegian y Alshawabkeh, 2013) y los procesos microbiológicos (He, Chu y Ivanov, 2013), entre otros. Estos métodos son menos invasivos, rentables para áreas extensas y prácticos cuando el tratamiento puede afectar la capacidad admisible de los cimientos durante el procedimiento (Marasini y Okamura, 2015a).
En ese sentido, este documento tiene como propósito presentar una revisión bibliográfica sobre la desaturación de suelos licuables mediante el proceso de inyección de aire, enfatizándo en los aspectos prácticos y consideraciones sobre la geotecnia de los suelos tratados. Además, se plantea una modelación numérica, considerando un flujo bifásico incompresible e isotérmico en medios porosos isotrópicos homogéneos con efectos capilares, para evaluar el efecto de la presión de inyección de aire y la permeabilidad del suelo sobre el radio de desaturación, mediante un análisis paramétrico a través del software FlexPDE, con su configuración gratuita (PDE Solutions Inc., 2005), que proporciona herramientas para la solución de ecuaciones diferenciales parciales.
EFECTO DEL GAS EN LA RESISTENCIA A LA LICUEFACCIÓN
En los últimos años se ha estudiado la desaturación del suelo y su influencia en la susceptibilidad a la licuefacción (Tsukamoto, Kawabe, Matsumoto y Hagiwara, 2014). Algunos de los estudios más significativos que muestran el efecto de la desaturación del suelo en el incremento de su resistencia se describen a continuación: según pruebas cíclicas informadas por Yang, Savidis y Roemer (2004); Tsukamoto et al. (2002), y Bouferra, Benseddiq y Shahrour (2007), se define que la reducción en el grado de saturación puede resultar en un aumento significativo en la resistencia a la licuefacción. Por otro lado, Ishihara, Huang y Tsuchiya (1998) demuestran que la rigidez volumétrica de los fluidos varía con la inclusión de un pequeño volumen de gas, afectando la respuesta de la presión de poros, el valor del parámetro B de Skempton, la onda P y la resistencia cíclica. Sobre la respuesta en presión de poros, Yang, Savidis, Sato y Li (2003) muestran que una reducción de la saturación en un 1 %, implica una reducción en la proporción de exceso de presión de poros de 0,6 a 0,15 bajo excitación horizontal pura. Además, Rad, Vianna y Berre (1994) encontraron que la arena con gas no soluble es más resistente que la que contiene gas soluble; igualmente, el modelo definido por Grozic, Nadim y Kvalstad (2005) permite concluir que la resistencia al corte no drenado del suelo gaseoso aumenta con una reducción en el grado de saturación.
Asimismo, Grozic, Robertson y Morgenstern (1999) indican que, bajo compresión no drenada, la arena suelta muestra una transición del ablandamiento al endurecimiento por deformación para grados de saturación menores a 90 %. Por otra parte, sobre pruebas cíclicas con un grado de saturación del 75 % al 99 %, el gas aumenta la resistencia cíclica del 200 % al 300 %. La figura 1 muestra una recopilación de datos experimentales tomados de varias fuentes literarias donde se muestra el aumento de la relación de resistencia a la licuefacción a medida que disminuye el grado de saturación (S w ), presentando diferentes variaciones de acuerdo con el tipo de suelo ensayado, lo que indica la incidencia de otros factores sobre la respuesta de las arenas ante cargas dinámicas.

Fuente: elaboración propia
Figura 1 Relación entre S w y la relación de resistencia a la licuefacción definida por el criterio de deformación axial de doble amplitud del 5 % después de 20 ciclos de carga (DA = 5 %)
En la figura 1 se unificaron algunos tipos de suelo y se definieron las líneas de regresión para arena de Urayasu (línea verde / R2=0,87), arena de Toyoura (líneas negras / R2=0,95-0,99), arena de Niigata (línea roja / R2=1,00) y arena Inagi (líneas azules / R2=0,55 y 0,92). Los resultados obtenidos indican que se explica alguna porción de la variabilidad de los datos en respuesta a sus valores medios. Se observa que los datos con mayor dispersión respecto de su media, ordenados de mayor a menor, son los asociados a la Arenas Inagi, Urayasu, Toyoura y Niigata, respectivamente. Además, se logra percibir que la saturación de la fase líquida se asocia fuertemente en un sentido inverso con la relación de resistencia a la licuefacción.
Implementación in situ
Algunos autores como Okamura et al. (2011); Okamura y Tomida (2015), y Tomida (2014) han implementado esta técnica para mejorar la resistencia a la licuefacción de arenas. En las pruebas in situ presentadas por Okamura et al. (2011), el flujo de aire se aplica desde el inyector a un estrato licuable hasta alcanzar una extensión de desaturación parcial de 4 m medidos horizontalmente con respecto al inyector, de lo que se obtiene una variación del grado de saturación (S w ) entre 68 % y 98 %. Posteriormente, los autores realizaron las pruebas cíclicas cuyos resultados indicaron que la resistencia a la licuefacción se duplica. Los mismos autores mencionan que los materiales utilizados son de fácil adquisición, sin necesidad de ningún equipo especializado para su diseño e implementación.
La técnica de desaturación in situ consiste en la inserción de una tubería en los estratos de suelos licuables por donde es inyectado el aire a presión, como se muestra en la Figura 2. Entre las ventajas de este método se destaca la poca perturbación para las operaciones de superficie, la eficiencia, el corto tiempo de ejecución, el bajo costo, la aplicabilidad en zonas de difícil acceso y la posibilidad de integración con otras tecnologías para aumentar la eficiencia; igualmente, no implica la extracción, el tratamiento, el almacenamiento o la liberación de agua subterránea. Información extrapolable de la técnica de volatilización in situ, sobre las especificaciones y operación que puede llegar a fortalecer los desarrollos de la inducción parcial del grado de saturación mediante inyección de aire, se encuentra en US EPA (1992), Wisconsin DNR (1995), y Holbrook et al. (1998).
Longevidad del efecto de inyección de aire
El área desaturada y el radio de influencia se han estudiado mediante pruebas centrífugas: un ejemplo de esto es el trabajo de Okamura y Tamura (2004) donde investigan zonas que fueron desaturadas anteriormente (4, 8 y 26 años atrás). Las pruebas de laboratorio demostraron que para la zona mejorada hace 26 años todavía existían burbujas de aire; además, ninguna de las muestras de las zonas tenía más del 90 % de S w . En un estudio similar, Okamura y Teraoka (2005a) observaron aumentos del 10 % para S w , lo que indica longevidad de las burbujas inyectadas, por lo que generar grados de saturación por debajo del 90 % produce condiciones de desaturación duraderas. Estudios reconocen que la longevidad del aire dentro del suelo típicamente es mayor a los diez años (Okamura, Ishihara y Tamura, 2006; Okamura et al., 2009; Vega, Ramos y García, 2017). Zeybek y Madabhushi (2017c) estudiaron la durabilidad de las burbujas en condiciones hidrostáticas, a baja y alta presión de poros, flujo vertical ascendente y descendente, presión de poros variable y agitación lateral. Su estudio revela que el volumen de burbujas ocluidas arrastradas por el flujo de agua a través de la matriz del suelo es mínimo y que la mayoría de las burbujas permanecen atrapadas en los poros del suelo. Los resultados incluso respaldan los mostrados por Eseller-bayat et al. (2013).
Evaluación de área desaturada y radio de influencia
Para medir el radio de influencia de la inyección de aire, Ishihara, Okamura y Oshita (2003) ejecutaron una prueba centrífuga en un ensamblaje donde el aire se inyecta verticalmente a un modelo de suelo saturado, y encontraron que el diámetro de la región desaturada es de 5,0 m para una inyección de 95 kPa. Tomida (2014) realizó pruebas similares a un terraplén con una presión de inyección de 80 kPa y descubre que el radio de desaturación aumenta con la presión y el tiempo de inyección, y se extiende a 9 m en 18 horas. Por otro lado, al comparar el método de desaturación con el método de pilas de arena compactada con distribución espacial típica menor a 2,5 m y presiones de inyección de 500 kPa, se reconoce que las pilas son conservadoras, ya que el suelo no solo se rigidiza sino que también es desaturado durante la inyección de compactación (Ishihara, Okamura y Oshita, 2003). Igualmente, el método de volatilización también se ha usado en suelos con presencia de contaminantes, y el trabajo de Lundegard y LaBrecque (1995) muestra métodos de medición del radio de influencia del suelo desaturado in situ. Se resalta que la medición precisa del radio de influencia permite un funcionamiento adecuado del sistema (Reddy y Adams, 2001). Un esquema típico del equipo de campo para volatilización de solventes se presenta en la figura 3.
Presión de inyección
Según Marulanda, Culligan y Germaine (2000), la presión de inyección debe ser mayor que la suma de la presión asociada a la cabeza de agua y las presiones capilares en el punto de inyección, y no debe exceder los esfuerzos efectivos en dicho punto para evitar fallas y agrietamiento del material. Experimentalmente, la presión de inyección a la que el suelo comienza a agrietarse equivale al 80 % de los esfuerzos efectivos más la presión debida a la cabeza de agua en el punto de inyección (Okamura et al., 2011). Yasuhara, Okamura y Kochi (2008) encontraron que a mayor presión de inyección más amplia y uniforme es la desaturación del suelo, algo consistente con el trabajo de Zeybek y Madabhushi (2018). Por otro lado, Zeybek y Madabhushi (2017b) demostraron que la generación de un asentamiento excesivo de los suelos durante el proceso de inyección se da por presión de inyección excesiva que altera la estructura del suelo y causa grietas y fisuras, particularmente cerca del punto de inyección. Se reconoce que, aunque el aumento en la presión de inyección se considera una forma rápida y eficiente de desaturar y, en efecto, aumentar la resistencia a la licuefacción, esto debe abordarse en detalle, particularmente en el caso de la inyección bajo fundaciones superficiales.
Ogata y Okamura (2006) sugieren que la presión de inyección teórica máxima por encima de la cual el esqueleto del suelo se altera es (P inj ) max = P hyd + 0,5σ’v, donde (Pinj)max, Phyd y σ’v son la presión máxima de inyección, la presión hidrostática y el esfuerzo vertical efectivo en el punto de inyección, respectivamente. Además, Zeybek y Madabhushi (2017b) muestran que los asentamientos inducidos por la inyección son inevitables, independientemente de la presión de inyección. Sin embargo, según las observaciones, Zeybek y Madabhushi (2018) sugieren que la magnitud de los asentamientos puede reducirse significativamente si: a) se controla la respuesta de la fundación aumentando la presión gradualmente; b) la presión de inyección neta aplicada, (Pinj)net = (Pinj)net = (Pinj)max - (Pinj)min y es inferior al 10 % de σ’v . Sin embargo, una presión de aire baja se convierte en un desafío para alcanzar áreas de desaturación uniformemente distribuidas y las burbujas de aire podrían tomar rutas de flujo preferenciales (Reddy, Kosgi y Zhou, 1995).
Experimentación
De acuerdo con los resultados obtenidos de ensayos realizados en mesa vibratoria (Camp, Camp y Andrus, 2010; Kohno y Nishigaki, 1982), centrífuga (Zeybek y Madabhushi, 2017b) y en campo (Okamura et al., 2011), es posible demostrar que el área de influencia y distribución del S w se ve afectada por el tipo de suelo, la estratificación, la presión y la profundidad de inyección (Yasuhara, Okamura y Kochi, 2008). Por otro lado, en el trabajo presentado por Zeybek y Madabhushi (2017a), se observa que el S w también se ve influenciado por la ocurrencia de cargas cíclicas, presentando un aumento de 0,64 % y 0,41 % para aceleraciones altas y bajas, respectivamente; información complementaria se encuentra en Marasini y Okamura (2015b). Ishihara, Okamura y Oshita (2003) desarrollaron pruebas de cortante cíclico no drenado en muestras con S w entre 68,8 % y 92,6 %, indicando que la relación de esfuerzos para el suelo desaturado dobla la condición saturada. Resultados similares se pueden observar en Okamura et al. (2009); Okamura, Ishihara y Tamura (2006); Okamura, Ishihara y Tamura (2003), y Okamura et al. (2011). Particularmente, Okamura, Ishihara y Tamura (2003) dejan claro que la resistencia al cortante cíclico de arena suelta puede mejorarse, pero el comportamiento de la deformación no cambia ya que la fase sólida permanece en una condición suelta. En otro orden de ideas, Okamura y Noguchi (2009) muestran que la resistencia a la licuefacción es proporcional a la succión matricial, siendo una relación creciente mayor que la del esfuerzo neto, y Zeybek y Madabhushi (2018) observan que la desaturación es menos consistente a profundidades con esfuerzos de confinamiento bajos y que la presencia de burbujas de aire minimizan la profundidad de licuefacción.
Zeybek y Madabhushi (2017a), 2017b) estudiaron la deformación del suelo desaturado con y sin cimentaciones superficiales y después de cargas dinámicas, obteniendo una reducción del asentamiento postsísmico (reconsolidación) y de las deformaciones desviadoras al disminuir el grado de saturación; esto llevó al incremento de la capacidad de carga posterior a la sacudida, pero intensificando las aceleraciones transferidas a la fundación. Así mismo, Marasini y Okamura (2015a) analizaron un suelo con S w entre 100 % y 85 % portante de cimientos poco profundos, lo que resulta en que la desaturación limita el asentamiento de la fundación (un 70 % y 50 % en los modelos de carga liviana y pesada, respectivamente) y la generación de exceso de presión de poros (un 50 % y 70 % menos que el saturado), evitando la licuefacción. Igualmente, Okamura y Teraoka (2005a) establecen que después de la prueba cíclica, el asentamiento para el suelo desaturado equivale a aproximadamente la sexta parte del obtenido para el suelo saturado. Un análisis similar con y sin cimentación es presentado por Takemura et al. (2009) y complementado por Okamura y Teraoka (2005a), lo que muestra que la inyección de aire tiene efectos significativos en la resistencia a la licuefacción para profundidades superiores a 2,0 m.
Modelación numérica
En algunos de los trabajos realizados para modelar la desaturación de suelos por el método de desaturación, se destaca la utilización del simulador de flujo multifásico TOUGH2 (Pruess, 1991), con el cual se ha logrado replicar la desaturación para diferentes presiones de inyección en el tiempo y espacio, obteniendo una concordancia entre mediciones experimentales y numéricas (Yasuhara, Okamura y Kochi, 2008). Okamura et al. (2011) muestran que las predicciones de desaturación son coherentes con imágenes por tomografía y con muestras de laboratorio. Por otro lado, Mitsuji (2008) predice la respuesta dinámica con un análisis de esfuerzo efectivo, indicando que la velocidad, los desplazamientos y la deformación por cortante disminuyen debido a la desaturación. Así mismo, Gao, Liu y Yu (2013) estudian la evolución del exceso de presión de poros durante una desaturación variable. Estudios similares llevados a cabo por Yashima, Oka, Taguchi y Tateishi (1995) abordan el terremoto de Hyogoken Nambu de 1995 en Port Island (Kobe, Japón), calculando y replicando el exceso de presión de poros y la aceleración como respuestas a cargas dinámicas.
Por otro lado, Marasini y Okamura (2015b) utilizan el modelo LIQCA 2D propuesto por Oka et al. (1999) y Oka et al. (1994), donde se simula el módulo volumétrico del fluido para un S w = 8 5%, replicando el exceso de presiones de poros, el asentamiento estructural y deformación de los suelos de fundación observados en pruebas de centrífuga. Takemura et al. (2009) muestran que la resistencia a la licuefacción para predicción y experimento, con S w = 80 %, es aproximadamente 2,5 veces la de la saturación total. McCray (2000) presenta el estado del arte de los modelos matemáticos de volatilización de solventes, e indica que los resultados están ligados a una debida calibración; además, resalta que dichos modelos pueden adaptarse a las necesidades de la técnica de desaturación. Es de mencionar que la infiltración de aire, la desaturación y la deformación son procesos concurrentes que deben predecirse rigurosamente. En este sentido, trabajos como el de Ramos (2015), desde metodologías de estado crítico, o el de Ramos, Prada y Vega (2016), que evalúan esfuerzos y deformaciones en suelos granulares de manera rigurosa, son valiosos.
MODELO MATEMÁTICO
La formulación matemática presentada por Pinder y Gray (2008), que se basa en el trabajo realizado por Darcy (1983), se propone en este trabajo. Considerando el flujo bifásico en un medio poroso, las ecuaciones (1) y (2) de balance para las fases no humectante, subíndice i=nw, y humectante, subíndice i=w, son como sigue:
Donde: θ es la porosidad total; S i es el grado de saturación del fluido i (w=agua, nw=aire); t es tiempo; k int es permeabilidad intrínseca del material (m2); k r,i es la permeabilidad relativa asociada al fluido i; μ i es la viscosidad dinámica del fluido i (Pa s); p i es la presión del fluido i (Pa); ρ i es la densidad del fluido i (kg/m3); g es la aceleración de la gravedad; y D es la coordenada de la elevación vertical (m). La saturación de las fases se puede expresar mediante la ecuación (3):
La presión capilar a escala macro (pc) se puede definir como la ecuación (4):
Las expresiones anteriores simplifican las ecuaciones. (1) y (2), eliminando dos incógnitas, y la ecuación de conservación de masa del fluido en los poros solo depende de p nw y S nw . Dado que la presión capilar se rige por S w , el término capilar, ∇p c , se puede expresar como la ecuación (5):
Sustituyendo las ecuaciones (3), (4) y (5) en la ecuación (1) y agregando la ecuación (2), el sistema de conservación de la masa se escribe en forma de presión saturación y se expresa en las ecuaciones (6) y (7), respectivamente, como:
A partir de las propiedades hidráulicas de los suelos no saturados, el grado efectivo de saturación de la fase w viene dado por la ecuación (8):
Donde: S max y S min son los valores límite máximos y mínimos de la fase líquida (S w ), respectivamente. La permeabilidad relativa de las fases de agua y aire viene dada por las ecuaciones (9) y (10), respectivamente:
Donde: a y b son los parámetros de forma y m un parámetro de material. Ahora, la expresión para la curva característica suelo y agua viene dada por la ecuación (11) (Van Genuchten, 1980):
Donde: a y b son los parámetros de forma y m un parámetro de material. Ahora, la expresión para la curva característica suelo y agua viene dada por la ecuación (11) (Van Genuchten, 1980):
Donde: n es un parámetro de material que cumple la expresión m= 1 - (1/n), y α es el inverso del valor de entrada de aire, el cual forma parte del modelo de Van Genuchten (1980). Derivando la ecuación (11), el término capilar en la ecuación (6) se expresa como la ecuación (12) (equivalente al trabajo de Horgue et al. (2015):
ANÁLISIS Y MODELACIÓN DE INYECCIÓN DE GAS EN MATERIAL SATURADO
Validación del modelo propuesto
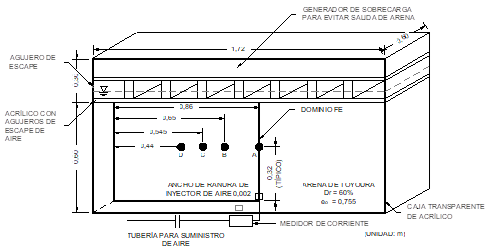
Yasuhara, Okamura y Kochi (2008) desaturaron por inyección de aire una columna de suelo completamente saturada, y realizaron la validación por medio de un análisis numérico. Las condiciones experimentales fueron: flujo de agua y aire en la parte superior de la caja, presión hidrostática inicial para fase húmeda, y flujo de aire a través de un inyector en la parte central inferior de la caja. La figura 4 muestra un esquema del montaje utilizado por los autores.
Fuente: modificado de Yasuhara, Okamura y Kochi (2008).
Figura 4 Esquema caja acrílica transparente. Los valores de S w se miden en los lugares A, B, C y D
Los resultados de Yasuhara, Okamura y Kochi (2008) se utilizan para validar la formulación matemática y el análisis numérico propuesto en el presente trabajo. Los parámetros del suelo, las presiones de inyección y las condiciones iniciales y de frontera utilizadas por Yasuhara, Okamura y Kochi (2008) son presentados en la tabla 1 y en la figura 4, respectivamente.
Tabla 1 Parámetros de material e hidráulicos utilizados para predicciones
| Variable | Magnitud | Descripción |
| r w | 1000kg/m3 | Densidad de fluido, fase húmeda |
| m w | 1x10-3 P a s | Viscosidad dinámica, fase húmeda |
| r nw | 1,28 kg/m3 | Densidad de fluido, fase no húmeda |
| m nw | 1,81x10-5 P as | Viscosidad dinámica, fase no húmeda |
| q | 0,421 | Porosidad |
| S max | 1,0 | Máximo grado de saturación, fase de húmeda |
| a | 2,237 x 10-4 1/P a | Parámetro α de Van Genuchten |
| n | 8,696 | Parámetro material 𝑛 Van Genuchten |
| a | 0,50 | Parámetro de forma, fase de húmeda |
| b | 0,33 | Parámetro de forma, fase de no húmeda |
| k int | 2,04 x 10-11 m2 | Permeabilidad intrínseca |
Fuente: Yasuhara, Okamura y Kochi (2008).
La figura 5 muestra la comparación de los resultados experimentales y numéricos de Yasuhara, Okamura y Kochi (2008) con el análisis numérico de desaturación propuesto en este trabajo. La figura 5a ilustra discrepancias entre los resultados experimentales en Yasuhara, Okamura y Kochi (2008) y las predicciones con el enfoque propuesto en este trabajo. Estas discrepancias se atribuyen directamente a inconsistencias experimentales y problemas de calibración de sensores que se obtuvieron en el experimento de Yasuhara, Okamura y Kochi, y en menor medida podrían también deberse a irregularidades entre permeabilidades reales y medidas, y la curva característica.

Fuente: elaboración propia
Figura 5 Comparación entre el presente trabajo y predicciones de Yasuhara, Okamura y Kochi para Sw
De igual manera, Yasuhara, Okamura y Kochi (2008) al respecto de sus resultados, expresan que los flujos predichos subestiman las mediciones experimentales, sin embargo, cuanto mayor es la presión de inyección, menor es la discrepancia. Además, las predicciones indican que el aire llega a la ubicación D, lo cual es no es congruente con las mediciones experimentales. Sin embargo, para otras ubicaciones A, B y C, y para tiempos mayores, las predicciones se acercan a las reales a medida que aumentan las presiones de aire. Por otro lado, se piensa de igual manera que las características de drenaje del suelo pudieron no replicarse teóricamente, por circunstancias asociadas a los experimentos de retención de agua. En otras palabras, Yasuhara, Okamura y Kochi (2008) mencionan que las propiedades como permeabilidad intrínseca y relativa, y características de drenaje del suelo deben examinarse con rigurosidad, antes de realizar predicciones del fenómeno.
La figura 5b muestra un comparativo entre las predicciones de Yasuhara, Okamura y Kochi (2008) y las predicciones con el enfoque propuesto en este trabajo. Se resalta que la figura 5 se presenta hasta los 6000 s, esto se debe a que los experimentos planteados por Yasuhara, Okamura y Kochi (2008) se efectuaron hasta dicho periodo. Además, el grado de saturación residual al final del experimento es de aproximadamente el 86 %.
Por otro lado, para las predicciones del presente estudio se percibe que para los puntos B, C y D se alcanza un grado de saturación a los 6000 s similar al del estudio de Yasuhara, Okamura y Kochi (2008), pero para el punto D se nota que en el proceso de saturación hay un grado se saturación a los 6000 s menor que el determinado en el experimento de Yasuhara, Okamura y Kochi (2008). Sin embargo, al final de la predicción se percibe que la cantidad de aire atrapado, después de que se detiene la inyección de aire, es independiente de la presión de inyección y está estrechamente ligado al campo gravitacional. Esta figura muestra una similitud entre los resultados obtenidos por las dos metodologías. Sin embargo, se observa un retraso de tiempo del S w en A, B, C y D, de los resultados de Yasuhara, Okamura y Kochi (2008), explicado por las diferencias entre las metodologías de los modelos numéricos y las funciones de permeabilidad relativa.
Al comparar ambas simulaciones numéricas se observan las siguientes tendencias: 1) S w inicialmente disminuye cerca del inyector y progresivamente alrededor, debido a las fuerzas boyantes y los gradientes inducidos; 2) hay tendencia similar en desaturación, así como un valor mínimo equivalente de S w al final de la inyección en t = 5500 s, y 3) después de t = 5500 s, el S w aumenta debido al apagado del inyector; no obstante, el aire permanece en el dominio, implicando valores de S w cercanos a 0,9 en t = 6000 s. Por tanto, a partir de las simulaciones, se observa que el flujo bifásico implementado en el modelo de elementos finitos propuesto captura las tendencias generales de la predicción y del experimento mostradas por Yasuhara, Okamura y Kochi (2008).
Análisis paramétrico de inyección de aire
Se realiza un estudio paramétrico para evaluar la influencia de la permeabilidad intrínseca y las presiones de inyección en el avance de aire dentro del suelo. Se seleccionaron tres tipos de suelo, cuyos parámetros hidráulicos se presentan en la tabla 2, obtenidos de Lu y Likos (2004). Estos parámetros son considerados representativos de arenas y arenas limosas, siendo sometidos a presiones de inyección de aire que varían de 75 a 85 kPa. En el presente análisis, la presión de inyección máxima de modo que el esqueleto del suelo se altere poco durante la inyección de aire, es equivalente a 87 kPa (para un inyector ubicado a 6,0 m bajo la superficie y un suelo con γ = 19,0 kN⁄m3) según lo sugerido por Ogata y Okamura (2006).
Tabla 2 Parámetros utilizados para el grupo de simulaciones
| Suelo | α(1/kPa) | n | kint (m2) |
|---|---|---|---|
| 1 | 0,07 | 2,0 | 5,55x10-12 |
| 2 | 0,10 | 4,0 | 1,00x10-11 |
| 3 | 0,12 | 6,0 | 5,55x10-11 |
Nota: α= 3; 0; b = 0; 33; ρw = 1000 kg/m3; μw = 1 x 10-3 Pa; ρnw = 1; 28 kg/m3; μnw =1;81 x 10-5 Pa; θ = 0; 34; Sw;max = 1; 0 y Sw;min = 1; 0. Datos de (Chen, Hopmans y Grismer (1999)
Fuente: elaboración propia.
El modelo utilizado consiste en un suelo homogéneo con dimensiones de 30 m de ancho y 15 m de profundidad (figura 6). Para la fase gaseosa, se asigna una condición de impermeabilidad al fondo, y se permite flujo de gas en el resto de fronteras, así como en el punto donde se encuentra el inyector a 6,0 m de profundidad. Las simulaciones inician desde una condición saturada y la fase gaseosa fluye cuando la presión generada en el inyector supera la presión hidrostática.
La figura 7 presenta los isocontornos de la evolución de S nw en t = 1800 s como función de la presión de inyección y la permeabilidad intrínseca. Se aclara que los isocontornos corresponden a un zoom fijo con forma cuadrada de 8,8 m de lado, ilustrado con líneas discontinuas en la figura 6. El borde inferior izquierdo del zoom se encuentra en las coordenadas x = 10,6 m y y = 7,2 m. En la misma figura se observa que, para una presión de inyección fija, cuanto más permeable es el suelo, mayor es la infiltración de la fase gaseosa. En consecuencia, para permeabilidades fijas e incrementos de presión de inyección de aire, se observa un aumento del avance del frente de desaturación, siendo en todos los casos, predominantemente vertical debido a las fuerzas gravitacionales.

Fuente: elaboración propia
Figura 7 Isocontorno de S nw en función de P nw, inj para t = 1800 s. Distancia en metros
Por otro lado, la predicción del impacto de la permeabilidad y la presión de inyección en el flujo de la fase gaseosa y el radio efectivo se muestra en la figura 8. Se selecciona el valor de S nw = 0,1 porque, como lo muestran Chaney (1978) y Yoshimi, Tanaka y Tokimatsu (1989), la susceptibilidad a la licuefacción de arenas completamente saturadas disminuye a la mitad cuando el grado de saturación del suelo se reduce en 10 %. Debido a que el aire inyectado penetra y genera un radio efectivo desde el inyector, este definirá el patrón (triangular o cuadrado) y el espaciado de las perforaciones de inyección de aire que deben diseñarse en función de los requisitos del proyecto y la cobertura completa del área susceptible a licuefacción dentro de la profundidad a mejorar.
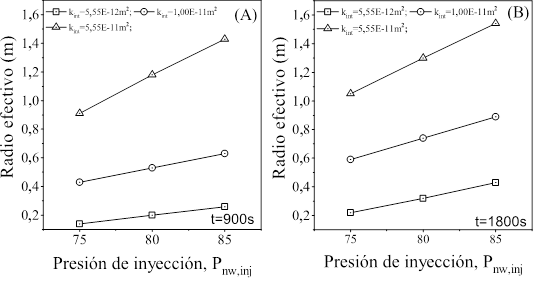
Fuente: elaboración propia
Figura 8 Radio efectivo para los suelos en la tabla 2S nw = 0,1 y P nw,inj de 70 a 85 kPa
Las lecturas de las magnitudes del radio de desaturación de las figuras 8A y 8B se tomaron en tiempos iguales a 900 s y 1800 s, respectivamente. Dichas figuras presentan los valores de radio efectivo para los suelos de la tabla 2, lo que indica que para todas las presiones el radio efectivo aumenta con el tiempo y el efecto es mayor a presiones de inyección más altas. Las figuras también muestran que, para una misma presión de inyección, se observa un incremento del radio efectivo de desaturación a medida que se incrementa la permeabilidad intrínseca del suelo. Asimismo, cuando se comparan las figuras 8A y 8B se ven resultados para iguales presiones más cercanos en el suelo menos permeable y más distantes en el suelo más permeable. En dichas figuras se observa que para valores bajos de permeabilidades intrínsecas, el radio efectivo crece lentamente con incrementos en la presión de inyección; en cambio, para el suelo más permeable, el aumento en el radio efectivo es más pronunciado.
CONCLUSIONES
La inducción parcial del grado de saturación en suelos para la mitigación de la licuefacción sigue siendo una tecnología relativamente nueva que necesita ser estudiada. Se debe profundizar en la comprensión de los mecanismos del flujo en medios porosos, en busca de mejorar su implementación en casos reales, ya que la mayor parte del trabajo de laboratorio realizado hasta el día de hoy incluye simplificaciones que pueden restringir la aplicabilidad de los resultados. De igual forma, como consecuencia de los pocos sistemas diseñados, operados y monitoreados en campo, no existen datos suficientes de rendimiento que permitirían reconocer con mayor certeza las ventajas y limitaciones de la técnica.
Por esto, es fundamental investigar sobre el control más preciso del grado de saturación generado en los suelos por procesos de inyección de aire, así como su distribución y extensión, la longevidad del efecto de desaturación y su rentabilidad respecto al área de ejecución.
Como resultado de este trabajo, se ha establecido una implementación para la predicción del flujo bifásico en el suelo a través de los criterios (estándares) de un flujo bifásico isotérmico, incompresible e inmiscible con impactos de succión matricial. Los resultados numéricos del modelo están en concordancia con los obtenidos por Yasuhara, Okamura y Kochi (2008). Por otro lado, se muestran discrepancias significativas con respecto a las mediciones experimentales desarrolladas por los mismos autores.
De los modelos realizados se puede concluir que el grado de saturación de la fase húmeda disminuye, sobre todo, cerca del inyector y progresivamente hacia arriba, representando el avance del frente de gas. De igual forma, a medida que la presión de inyección de gas es mayor, el grado de saturación de la fase húmeda disminuye, lo que permite gradientes más altos para el flujo de gas. Por otra parte, se encontró que, para suelos con baja permeabilidad, el radio efectivo es relativamente pequeño para presiones bajas y altas de inyección; por el contrario, cuando la permeabilidad es mayor, se obtienen mayores variaciones del radio efectivo en el mismo instante de tiempo, causado principalmente por las fuerzas boyantes y los gradientes inducidos.
Por último, la magnitud de la extensión del frente de la fase gaseosa durante y después del proceso de inyección de aire está fuertemente controlada por la permeabilidad intrínseca y la presión de inyección, como lo indica el análisis paramétrico efectuado.