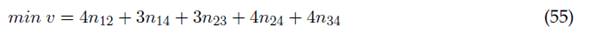Introducción
Históricamente, el objetivo del planeamiento de las redes eléctricas se basaba en cumplir con la curva de demanda a un costo mínimo. Actualmente, son diversas las restricciones operativas que se deben incluir: valor de la capacidad de las fuentes de suministro, aspectos de la estabilidad, adquisición de reservas, comportamiento del almacenamiento e integración de otros sectores energéticos (Helistö et al., 2019).
El planeamiento óptimo de sistemas de transmisión (OPTS, por su sigla en inglés) es un problema complejo de programación matemática no lineal (Gayibov, 2020), como se describe en la ecuación (1), donde
 representa las restricciones de igualdad no lineales y restricciones de flujo de potencia,
representa las restricciones de igualdad no lineales y restricciones de flujo de potencia,
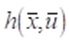 representa las restricciones de desigualdad no lineal, límites en las variables de control y límites operativos del sistema de potencia. Las restricciones, controles y objetivos se describen en la tabla 1.
representa las restricciones de desigualdad no lineal, límites en las variables de control y límites operativos del sistema de potencia. Las restricciones, controles y objetivos se describen en la tabla 1.
Tabla 1 Características de un problema de optimización para sistemas de potencia

Fuente: adaptado de Hajiabbas y Mohammadi-Ivatloo (2020).
Como estrategias de solución para el OPTS, durante los últimos años se han propuesto diversos métodos y algoritmos (Abdin y Zio, 2019; Fathi et al., 2019; Mohammadi-ivatloo y Nazari-Heris, 2019). Entre estos métodos se incluyen los de optimización convencionales (Nguyen y Santoso, 2021; Zhang, 2013), los de inteligencia de inteligencia artificial (Ruan et al., 2020), los heurísticos (Lu et al., 2007) y los metaheurísticos (Morquecho et al., 2021; Saldarriaga-Zuluaga et al., 2019). A continuación se presenta el modelo para algunas de las estrategias utilizadas para el OPTS.
Modelos de optimización para OPTS
En ciencias aplicadas y en ingeniería, un modelo es una representación que permite relacionar variables, parámetros y restricciones a través de formulación matemática (Chow y Sánchez-Gasca, 2020; Kaveh y Bakhshpoori, 2019; Soroudi, 2017). En el OPTS, los modelos permiten analizar costos, establecer ubicaciones y dimensionar equipos de acuerdo con la proyección de la generación y la demanda. En la actualidad se utilizan varios modelos para representar OPTS, entre ellos: modelo de transporte, modelo híbrido lineal, modelo DC, modelo lineal disyuntivo (Fathi et al., 2019; Haffner, 2000; Peñaherrera Wilches, 2015; Tapias-Isaza et al., 2011). En las tablas 2 y 3 se presenta la descripción de las variables y parámetros que se van a utilizar para la descripción de los modelos de OPTS.
Modelo de transporte
En Garver (1970), se formuló una metodología de modelado matemático utilizando programación lineal para resolver el problema de OPTS, aplicando el modelo de transporte. Este consiste en un modelo relajado que aplica la primera ley de Kirchhoff. La formulación matemática dada para este modelo se presenta en las ( ecuaciones 2) a (7).
Función objetivo:
Restricciones:
La ecuación (2) representa la función objetivo que busca minimizar el costo de inversión en la adición de nuevas líneas para solucionar el problema de OPTS. La ecuación (3) corresponde a la primera ley de Kirchhoff, la cual describe que la suma de las corrientes que entran a un nodo debe ser igual a la suma de las corrientes que salen de este estableciendo el adecuado funcionamiento del sistema. La ecuación (4) establece la restricción del flujo de potencia se puede transmitir por las líneas. La ecuación (5) establece la restricción de generación máxima y mínima que se puede generar por nodo. La ecuación (6) determina la cantidad de líneas máximas y mínimas que se pueden adicionar entre nodos. La ecuación (7) indica que el número de líneas adicionada debe ser un número entero y el flujo de potencia puede tomar valores positivos, negativos o cero.
Al tener en cuenta solo la primera ley de Kirchhoff, este modelo no otorga un resultado del todo real u óptimo, lo que representa una gran desventaja; sin embargo, permite resolver sistemas conexos y no conexos. Este fue el primer modelo usado con éxito en el OPTS (Gonzalo, 2017).
Modelo DC
Este modelo, a diferencia del de transporte, debe satisfacer las dos leyes de Kirchhoff. De acuerdo con esto, es ampliamente utilizado para resolver el problema de OPTS (Saldarriaga-Zuluaga et al., 2020). Debido a que para las líneas existentes y las posibles líneas nuevas adicionadas se consideran las dos leyes de Kirchhoff, el modelo es un problema no lineal entero mixto (Saldarriaga-Zuluaga et al., 2016). La formulación matemática dada para este modelo se representa en las ecuaciones (8) a (16).
Función objetivo:
Restricciones:
La ecuación (8) establece la función objetivo, la cual minimiza el costo de la inversión y la generación artificial adicionada o cortes de carga. La ecuación (9 ) representa la conservación de potencia en cada nodo, es decir, la primera ley de Kirchhoff. La ecuación (10) representa la segunda ley de Kirchhoff e indica la diferencia angular entre nodos y el flujo de potencia activa entre ellos. La ecuación (11) representa el límite de capacidad del flujo de potencia activa en las líneas. Las ecuaciones (12), (13) y (14) establecen los límites de generación, cantidad de líneas y generación ficticia, respectivamente. La ecuación (15) presenta la función del nodo de slack, o referencia, evitando la presencia de matrices que no tengan solución o que tenga infinitas soluciones. Por último, la ecuación (16) indica que el número de líneas adicionada debe ser un número entero, el flujo de potencia y generación artificial adicionada o cortes de carga puede tomar valores positivos, negativos o cero (0).
Modelo híbrido lineal
Indica un modelo intermedio entre el modelo DC y de transporte, ya que al aplicar la primera ley de Kirchhoff solo a las posibles nuevas líneas, se puede considerar como el modelo de transporte, mientras que al aplicar la primera y la segunda ley de Kirchhoff a las líneas existentes se asemeja al DC (Escobar Vargas, 2013). En este sentido, se puede formular un modelo híbrido lineal o uno híbrido no lineal.
Por la complejidad del modelo híbrido no lineal se busca un enfoque más simplificado como el modelo híbrido lineal (Peñaherrera Wilches, 2015). Este es un problema de programación lineal entera mixta, con formulación matemática representada en las ecuaciones (17) a (25).
Función objetivo:
Restricciones:
Al igual que en los anteriores modelos, la ecuación (17) determina la función objetivo, la cual minimiza el costo de la inversión en la adición de nuevas líneas para solucionar el problema de OPTS. La ecuación (18) indica la primera ley de Kirchhoff, pero, a diferencia de los otros modelos, los flujos se separan de acuerdo con líneas existentes y posibles nuevas líneas. La ecuación (19) establece la segunda ley de Kirchhoff, teniendo en cuenta únicamente al flujo en las líneas existentes. Las ecuaciones (20) y (21) representan el límite de capacidad del flujo de potencia activa en líneas existentes y líneas candidatas respectivamente. Por otra parte, las ecuaciones (22) y (23) corresponden a los límites superior e inferior de generación y de la cantidad de líneas entre nodos. La ecuación (24) establece el nodo referencia, o slack, en el sistema. La ecuación (25) indica que el número de líneas adicionada debe ser un número entero y el flujo de potencia puede tomar valores positivos, negativos o cero (0).
Modelo lineal disyuntivo
Es un modelo lineal que se deriva del modelo DC, debido a que a ciertas restricciones la solución óptima puede ser la misma (Moreno Tobar, 2019). Este modelo presenta la adición de variables binarias asociadas a las líneas que toman el valor de “1” si es necesario agregar una nueva y el valor de “0”, si no se necesita agregarla en el sistema existente, desagregando los términos cuadráticos a términos lineales (Félix Ruiz, 2018). La formulación matemática dada para este modelo se representa en las ecuaciones (26) a (34).
Función objetivo:
Restricciones:
La ecuación (26) representa la función objetivo la cual determina que se debe minimizar el costo de la inversión; cabe destacar que cuenta con la variable binaria a diferencia de los demás modelos. La ecuación (27) expresa la primera ley de Kirchhoff y, como se explicaba anteriormente en el modelo híbrido lineal, se separan los flujos de potencia de las líneas existentes de las líneas candidatos. La ecuación (28) determina la segunda ley de Kirchhoff aplicada solamente a las líneas existentes, mientras que la ecuación (29) representa la segunda ley de Kirchhoff para cada línea candidata; esto indica que el número de restricciones modeladas a través de la ecuación (29) depende del número máximo de líneas que se puedan adicionar (cada posible línea a adicionar tiene que ser considerado de forma independiente como una variable binaria). Las ecuaciones (30) y (31) indican la capacidad del flujo de potencia activa que tienen las líneas existentes y las líneas candidatas. Por ultimo, las ecuaciones (32) y (33) establecen los límites de generación que posee el sistema y los límites de la generación ficticia. La ecuación (34) indica que la variable de decisión es un valor binario es decir 0 o 1 y el flujo de potencia puede tomar valores positivos, negativos o 0.
Este artículo se divide en cinco secciones, incluyendo la introducción. En “Herramientas para el modelo de OPTS”, se presenta la descripción del software utilizado y un ejemplo del OPTS a través de esta herramienta. En “Metodología”, se desarrolla la explicación de la metodología de solución, y se presentan los casos de estudios. En “Resultados”, se analizan los resultados obtenidos. Finalmente, en “Conclusiones”, se presentan las conclusiones y el trabajo futuro.
Herramientas para el modelo de OPTS
Las herramientas para el modelo y simulación del OPTS son útiles debido a que permiten explorar preguntas de investigación y prototipos a un costo y tiempo menor. Los simuladores proporcionan un entorno virtual con una variedad de características deseables, que facilitan modelar criterios específicos y analizar su rendimiento en diferentes escenarios (Chaudhary et al., 2012). En el área de optimización, GAMS es un software diseñado para modelar y resolver problemas lineales, no lineales y optimización entera mixta. A continuación, se presenta una descripción del software GAMS, adicionalmente, se ilustra un ejemplo del OPTS a través de esta herramienta.
Software GAMS
GAMS es un sistema de modelización que ayuda a resolver problemas de optimización matemática, tanto de programación lineal, como no lineal y entera; consta de un compilador con su propio lenguaje que permite implementar modelos matemáticos complejos, donde se podrán aplicar un rango de solvers o solucionadores (Babu y Singh, 2016).
Para resolver problemas con GAMS, según el modelo, los usuarios deben seleccionar el solver; así, GAMS verifica si los términos son adecuados al modelo, por ejemplo, el tipo de modelo de programación lineal (LP, por su sigla en inglés) no maneja términos no lineales y discretos (binarios, enteros, etc.) (Harish Kumar y Mageshvaran, 2020). En la tabla 4 se presentan algunos de los modelos con los respectivos solvers que se pueden utilizar en GAMS.
Tabla 4 Tipos de modelos con los respectivos solvers disponibles en GAMS

Fuente: elaboración propia.
Para el ejemplo del OPTS, se utilizará el modelo MINLP, el cual se ocupa de modelar problemas no lineales con variables continuas, discretas o binarias, convirtiéndose en una gran herramienta para la solución de problemas, aunque es un modelo más complejo que los MIP o NLP (Furqan y Mawengkang, 2018). La formulación básica de este modelo se expresa en las ecuaciones (34) a (37), donde las funciones f son convexas y las variables 𝑥 son continuas y/o discretas.
Función objetivo:
Restricciones:
En Kronqvist et al. (2019), los solvers de GAMS que pueden solucionar el modelo MINLP son:
ALPHAECP: es un solver basado en una extensión del método plano de corte de Kelley capaz de solucionar un problema pseudoconvexo.
BARÓN: es un solver que utiliza algoritmos de branch and bound para reducir el rango de variables y dar una solución óptima determinista.
BONMIN: es un solver que cuenta con el algoritmo básico de branch and bound (B-BB), el algoritmo de descomposición de aproximación externa (B-OA), el algoritmo de aproximación externa basado en branch and bound (B-QG), y el algoritmo híbrido entre B-BB y B-QG (B-hyb).
COUENNE: es un solver que maneja el algoritmo de branch and bound espacial basado en LP, admitiendo variables continuas, binarias y enteras, pero no conjuntos especializados.
DICOPT: es un solver basado en una extensión del algoritmo de aproximación externa para la estrategia de relajación de la igualdad.
KNITRO: es un solver que resuelve problemas con funciones suaves a gran escala mediante un algoritmo que itera hasta ser resuelto el problema también conocido como gradiente reducido generalizado.
LINDOGLOBAL: es un solver que emplea algoritmos de branch and bound para dividir el problema en una lista de subproblemas en donde se produce una serie de restricciones se llega a la solución con un mínimo grado de tolerancia.
OQNLP: es un solver que utiliza algoritmos heurísticos de arranque múltiple, lo que proporciona diferentes valores iniciales y devuelve las posibles soluciones determinando la más óptima de todas.
SBB: es un solver que admite todo tipo de variables discretas que permite la combinación de modelos como branch and bound y otros de tipo NLP, donde se acortaran los límites de las variables creando submodelos hasta llegar a una solución óptima.
Ejemplo del OPTS a través del lenguaje GAMS
La figura 1 presenta un sistema de potencia de cuatro nodos (Escobar et al., 2010), el cual cuenta con dos generadores y cinco líneas de transmisión; se tiene la posibilidad de adicionar una línea más por cada una de estas líneas, con el objetivo de cubrir la demanda del sistema al menor costo posible. Los datos del problema y la topología del sistema se pueden observar en la figura 1. Este caso se plantea como el ejemplo para explicar de manera práctica el modelo de transporte para OPTS.
Formulación del problema
El primer paso es formular las ecuaciones sujetas a la primera ley de Kirchhoff, las cuales se aplican para cada nodo. Se consideran los flujos entrantes a los nodos como positivos y los que salen como negativos. La elección de los sentidos de los flujos se puede hacer de manera aleatoria, debido a que la solución arroja el sentido correcto de los flujos. De acuerdo con esto, las ecuaciones (39) a (42) representan la formulación de este primer paso.
Luego se procede a formular las ecuaciones (43) a (47), que representan el límite de capacidad de transmisión de cada línea.
Por otra parte, se plantean las restricciones sobre la capacidad de generación y el número máximo de adiciones permitidas de líneas, como se observa en las ecuaciones (48) a (54).
Finalmente se establece la función objetivo, como se muestra en la ecuación (55).
Implementación en GAMS
El segundo paso es implementar la formulación del problema en el software GAMS. Esta se realiza en seis pasos, los cuales se caracterizan por seis algoritmos; la tabla 5 presenta los pasos, los algoritmos y la respectiva descripción.
Tabla 5 Tipos de modelos con los respectivos solvers disponibles en GAMS

Fuente: elaboración propia.
Definición de conjuntos del modelo matemático. El algoritmo 1 inicia con la implementación del modelo matemático propuesto, con la definición de conjuntos; para ello se utiliza el comando “SETS”. En GAMS se debe definir los conjuntos que son los que recorren los vectores del problema y los rangos de elementos en que varían dichos conjuntos. En este caso se define el conjunto “g” que indica los generadores presentes en el sistema; para el ejemplo, existen dos generadores por lo que G1 y G2 son los elementos que componen este conjunto. El conjunto “i” tiene como elementos los nodos del sistema N1, N2, N3 y N4, también se define el conjunto “L” el cual es constituido por las líneas L1 (corredor 1-2), L2 (corredor 1-4), L3 (corredor 2-4), L4 (corredor 2-3) y L5 (corredor 3-4); por último “MAP(g,i)” es un conjunto que asocia los generadores con los nodos.

Algoritmo 1 Definición de conjuntos del modelo matemático para el ejemplo propuesto e implementado en GAMS
Definición de la matriz de incidencia, datos de las líneas y parámetros. En el algoritmo 2, se declara el comando “TABLE” que define una matriz de datos, donde “S” es la matriz de incidencia de los flujos del sistema y la tabla “Líneas” representa la matriz de datos de las líneas como costo, susceptancia, líneas existentes, el máximo número de líneas que se pueden adicionar en cada línea y el flujo de potencia activa máxima que puede pasar por cada línea.
Igualmente, en el algoritmo 2 se declara el comando “PARAMETER” para asignar valores a los elementos que componen cierto conjunto, en el ejemplo se implementa el “parameter D(i)” para asignar la demanda que tiene cada uno de los nodos, de la misma forma se designa el “parameter Gmax” para fijar el valor máximo que puede generar “G1” y “G2”.
Variables del modelo. En el algoritmo 3, el comando “VARIABLES” define las variables del problema las cuales se les asigna un valor, una vez GAMS complete la ejecución del código; por ejemplo “v” es el costo a minimizar, “pg(g)” es la generación de las fuentes existentes en el sistema, por lo que depende del conjunto “g”, y “f(L)” es el flujo que pasa por las líneas; por tal motivo depende del conjunto (L). De manera análoga se utiliza “INTEGER VARIABLE”, para determinar que las variables definidas dentro de este comando son variables enteras, así como “nij(L)”.
Límites máximos y mínimos, de la capacidad de las líneas a construir y de la generación. En el algoritmo 4, se delimitan las variables de generación y el número de líneas que se pueden adicionar. El “. up” significa el límite superior y “. lo” el límite inferior.
Ecuaciones en formato GAMS. En el algoritmo 5 se formulan las ecuaciones del modelo matemático a resolver. Una vez definidos las variables y sus límites se proceden a utilizar el comando “EQUATIONS”, el cual denota la función objetivo además de las restricciones del modelo matemático propuesto. En primer lugar, se escribe el nombre de la ecuación junto con una breve descripción de esta; si la ecuación depende de un conjunto, es necesario colocar el índice del conjunto entre paréntesis. Con base en lo anterior, se escriben las ecuaciones en formato GAMS, por ejemplo la función objetivo llamada “ObjFun” se formula con su nombre seguido de “..”, después se escribe la ecuación con sus variables donde se puede utilizar operaciones matemáticas. Los símbolos que se utilizan para denotar si es una igualdad o una inecuación se escriben: “=L=” (menor o igual), “=G=” (mayor o igual) y la igualdad “=E=”.
Comandos para obtener la respuesta óptima del problema con el tipo de modelo específico. En el algoritmo 6 se establece el solver a implementar y las variables que se van a optimizar para la solución del problema. Se coloca el comando “MODEL” seguido el nombre del archivo y “/ALL/”, esto indica que para la solución se deben tener en cuenta todas las restricciones definidas. Posteriormente se utiliza el comando “SOLVE” para establecer cuál tipo de modelo y qué variable se va a optimizar.
Finalmente, se compila el modelo descrito; si no se tiene ningún error de sintaxis en el código se despliega una nueva ventana en la que el software mostrará el desarrollo y solución del problema.
Resultados del OPTS en GAMS
En la tabla 6, se observan los resultados obtenidos por GAMS con el solver “DICOPT”; el costo óptimo para el problema ejemplo es de 24 PU, también se evidencia el flujo que pasa por las líneas y el total de líneas en cada uno de los corredores.
La figura 2 presenta la solución del OPTS para el sistema de cuatro nodos utilizando GAMS con el solver “DICOPT” para el modelo MINLP.
Metodología
En la figura 3 se presenta el diagrama de flujo para determinar los costos de expansión de sistemas de transmisión cuando se emplea un modelo matemático en el software GAMS. Está dividido en cinco etapas: la primera identifica el sistema de transmisión, la segunda establece el problema de planeamiento del sistema de transmisión, la tercera realiza la formulación del sistema de potencia de acuerdo con cada uno de los modelos de optimización, la cuarta aplica la formulación del sistema de potencia en el software GAMS y la última selecciona el costo óptimo.

Fuente: elaboración propia
Figura 3 Metodología para determinar los costos de expansión de sistemas de transmisión
Identificar datos del sistema de transmisión
Para este primer paso, es necesario determinar la topología del sistema con los elementos que lo componen, como los generadores, las cargas con su ubicación en el sistema, líneas existentes y número de nodos, esto con el objetivo de determinar los datos básicos necesarios para análisis de futuros estudios de planeamiento.
En este artículo, se presentan dos sistemas de potencia de prueba: Garver de 6 nodos y Sur Brasilero de 46 nodos, los cuales son utilizados en la literatura especializada (Alvarez et al., 2020; Correa Flórez et al., 2020; Das et al., 2020; De Oliveira et al., 2017; Ledezma y Alcaraz, 2020; Meneses et al., 2020) para la solución del problema de expansión para un sistema de transmisión.
Sistema de potencia Garver 6 nodos
Cuenta con 6 líneas, 3 generadores y 5 cargas (figura 4). La información del sistema a detalle se presenta en Haffner (2000).
Sistema de potencia Sur Brasilero 46 nodos
Cuenta con 46 líneas, 12 generadores y 19 cargas (figura 5). Es un sistema de tamaño y complejidad media. La información sobre los parámetros de sistema se puede consultar en Haffner (2000).
Establecer el problema de planeamiento de la expansión del sistema de transmisión
Una vez se tiene el caso de estudio y el respectivo análisis de flujo de carga, es necesario resolver la pregunta: ¿Qué elementos se requieren para satisfacer el crecimiento de la demanda y la inclusión de nuevas fuentes de generación a un mínimo costo de inversión?; es decir, cuál es el problema de planeamiento del sistema de transmisión a resolver. A partir del problema de planeamiento, se definen las variables asociadas de proyección: costo de construcción de nuevas líneas, flujo de potencia máximo que soporta cada línea, entre otras variables que permitan aplicar la formulación para resolver el problema a través de modelos de optimización. A continuación, se describen los problemas de planeamiento que se analizarán en los casos de estudio seleccionados.
Sistema de potencia Garver 6 nodos
Se pretende expandir el sistema con 15 líneas candidatas. Para este, existen dos casos de estudio: uno donde la capacidad de generación es igual a la demanda total (sin redespacho) y el otro donde la capacidad de generación es superior a la demanda total (con redespacho).
Sistema de potencia Sur Brasilero 46 nodos
Se pretende expandir el sistema con 79 líneas candidatas. Para este, existen dos casos de estudio sin redespacho y con redespacho.
Para la formulación del sistema Garver, se definió como función objetivo la ecuación (56), la cual representa la suma de los costos por el número de líneas adicionadas, por ejemplo, CL1∗L1=40∗ n 12 , así respectivamente con cada una de las líneas candidatas. En el modelo de transporte se toman en cuenta 36 restricciones (6 para la primera ley de Kirchhoff y 30 para el límite de capacidad de transmisión de cada línea). En el modelo DC se considera que el sistema no tiene generación artificial adicionada o cortes de carga, por eso la función objetivo será la misma ecuación (56), sujeta a 51 restricciones (6 para la primera ley de Kirchhoff, 15 para la segunda ley de Kirchhoff y 30 para el límite de capacidad de transmisión de cada línea). En el modelo híbrido lineal se maneja la misma función objetivo del modelo de transporte, sujeta a 81 restricciones (6 para primera ley de Kirchhoff, 15 para la segunda ley de Kirchoff teniendo en cuenta únicamente al flujo en las líneas existentes, 30 de la capacidad del flujo de potencia activa en líneas existentes y 30 de la capacidad del flujo de potencia activa en líneas candidatas).
A diferencia de los anteriores modelos, el modelo lineal disyuntivo por su variable binaria la función objetivo está dada por la ecuación (57), sujeta 291 restricciones (6 para la primera ley de Kirchhoff, 15 para la segunda ley de Kirchhoff de las líneas existentes, 120 para la segunda ley de Kirchhoff de cada línea candidata, 30 de la capacidad del flujo de potencia activa en líneas existentes y 120 de la capacidad del flujo de potencia activa en líneas candidatas)
Para la formulación del sistema de potencia Sur Brasilero se utilizó la función objetivo de la ecuación (58) para los modelos de transporte, DC e híbrido lineal. En el modelo de transporte se toman en cuenta 204 restricciones (46 para la primera ley de Kirchhoff y 158 para el límite de capacidad de transmisión de cada línea). En el modelo DC se tienen 283 restricciones (46 para la primera ley de Kirchhoff, 79 para la segunda ley de Kirchhoff y 158 para el límite de capacidad de transmisión de cada línea). El modelo híbrido lineal con 441 restricciones (46 para primera ley de Kirchhoff, 79 para la segunda ley de Kirchoff teniendo en cuenta únicamente al flujo en las líneas existentes, 158 de la capacidad del flujo de potencia activa en líneas existentes y 158 de la capacidad del flujo de potencia activa en líneas candidatas).
El modelo lineal disyuntivo tiene como función objetivo la ecuación (59), sujeta a 1547 restricciones (46 para la primera ley de Kirchhoff, 79 para la segunda ley de Kirchhoff de las líneas existentes, 632 para la segunda ley de Kirchhoff de cada línea candidata, 158 de la capacidad del flujo de potencia activa en líneas existentes y 632 de la capacidad del flujo de potencia activa en líneas candidatas).
Al tener los datos del sistema de transmisión, es esencial definir su formulación para así encontrar una configuración que produzca la menor inversión en el plan de expansión del sistema de transmisión (función objetivo), que cumpla con las condiciones adecuadas de operación de este sistema; para ello se caracterizan matrices y restricciones de cada sistema para los modelos de optimización lineales y no lineales. Esta formulación se describe en detalle en la introducción.
Aplicar la formulación del sistema de transmisión en el software GAMS
Una vez establecida la formulación de los modelos para cada uno de los sistemas de transmisión, se implementan en el lenguaje de programación del software GAMS anteriormente explicado, y se determinan los conjuntos, variables y parámetros del sistema de transmisión.
Seleccionar costo óptimo
La selección de los solver se realiza a través de un conjunto de pruebas, donde se incluye el análisis de la carga computacional y el costo óptimo. La prueba se realiza comparando uno a uno los solvers que se describen en la tabla 4 para el problema MINLP. Las tablas 7, 8 y 9 presentan la descripción de los modelos y solver a implementar de acuerdo con el sistema de potencia y con las pruebas realizadas entre solver.
GAMS ofrece un informe de resultados de manera clara y detallada, donde muestra la compilación de las ecuaciones, las variables y restricciones presentes en el modelo; esto conlleva a realizar la comparación de la formulación realizada y la obtenida al compilar GAMS, para verificar si el modelo se realizó de la manera correcta.
Resultados
Los resultados, de acuerdo con la información descrita en las tablas 7, 8 y 9, se presentan a través de las métricas de costo ( c 𝒊𝒋 )., cantidad de líneas a incluía ( 𝒏 𝒊𝒋 )., y el tiempo de simulación computacional. La implementación de los modelos se realizó en GAMS IDE 34, con excepción del modelo lineal disyuntivo, debido al solver se utilizó la versión GAMS 25.1.3. Como equipo de procesamiento, se utilizó un computador con un procesador Intel(R) Core(TM) i5-5200U CPU, 6 GB de RAM y sistema operativo Microsoft Windows 10 64-bit. A continuación se presentan los resultados para los dos casos de estudio implementado.
Sistema de potencia Garver 6 nodos/13
En las tablas 10 y 11 se presentan los resultados obtenidos para el sistema sin redespacho y con redespacho.
En la tabla 10 se evidencia que en las soluciones hay dos líneas que aparecen independiente del modelo, las cuales son: 𝑛 2−6 , 𝑛 4−6 ; en la tabla 4 se observa el mismo patrón pero con la línea 𝑛 3−5 . Esta característica indica que son líneas necesarias dentro de la solución del problema, por eso todos los modelos las identifican como líneas de interés, y que están conectadas directamente a los nodos de generación. En el modelo de transporte, debido a que tiene menos restricciones, se adiciona la línea 𝑛 1−5 .
Los resultados del costo óptimo para el caso sin redespacho son de 200×103 USD sin importar el modelo, mientras que, para el caso con redespacho, tomando el modelo DC como referencia (130×103 USD), los otros modelos tienen una diferencia porcentual de 15,38 %, como se observa en la figura 6.

Fuente: elaboración propia
Figura 6 Sistema Garver 6 nodos diferencia porcentual de costos para cada modelo
Análisis comparativo MATLAB
Con el objetivo de establecer si los modelos están bien desarrollados en GAMS, se realiza una implementación del caso de estudio en el MATLAB, para este análisis comparativo solo se aplica el modelo de transporte y el modelo híbrido lineal. Las tablas 12 y 13 presentan los resultados obtenidos.
Al comparar los resultados de las tablas 10 y 11 con los obtenidos en las tablas 12 y 13, además de los presentados en Mónica et al. (2012), se establece similitud en las métricas utilizadas; esto confirma que los modelos están bien desarrollados en GAMS y por tanto se puede continuar con la implementación del segundo caso de estudio. Es importante resaltar que para el sistema del Sur Brasilero no se implementa este análisis comparativo, debido a que el objetivo del trabajo es implementar los modelos de optimización en GAMS.
Sistema de potencia Sur Brasilero 46 nodos
En las tablas 14 y 15 se presentan los resultados obtenidos para el sistema sin redespacho y con redespacho.
Como se observa en la tabla 14, las líneas significativas para el caso sin redespacho son n 20-21 n 42-43, n 31-32, n 24-25 . Para el caso con redespacho, como se observa en la tabla 15, las líneas significativas son n20-21, n42-43. Para los dos escenarios, las líneas significativas son las que están asociadas a los nodos con mayor demanda del sistema: n 20-21 , n42,43.
Los resultados del costo óptimo para el caso sin redespacho son idénticos en el modelo DC y modelo lineal disyuntivo, con una diferencia porcentual de 8,46 % con el modelo híbrido lineal y de 17,58 % con el de trasporte. En el caso con redespacho también se presentó que el costo es el mismo en los modelos DC y lineal disyuntivo, teniendo una gran diferencia con el modelo de transporte de 26,81 %, como se observa en la figura 7.
Conclusiones
GAMS es un software que permite analizar el OPTS a través de modelos MINLP, se caracteriza por su baja carga computacional y por contar con diferentes solver. Estos, utilizados para resolver OPTS, pueden no encontrar una solución óptima debido a que los algoritmos que manejan se ven afectados por el número del sistema y por la complejidad del planeamiento de expansión del sistema.
Los modelos implementados presentaron desempeños equivalentes en el sistema de Garver de 6 nodos, esto se debe a que el sistema es pequeño. Para el sistema Sur Brasilero de 46 nodos, el desempeño de los modelos no presenta similitud, por el contrario, se identifican diferencias importantes en los resultados, lo que permite caracterizar solver específicos de acuerdo con el número de nodos. Desde el análisis de costo óptimo, el modelo DC y el modelo lineal disyuntivo presentaron para los dos sistemas de potencia el mayor costo respecto al modelo de transporte y al modelo híbrido lineal.
Trabajo futuro
Son diversos los análisis que se pueden realizar para el planeamiento de sistemas de potencia. Los modelos de optimización deben aprovechar los avances en software y hardware, las estrategias deben ser escalables para aliviar la carga computacional y poder resolver problemas de mayor complejidad. Los desafíos crecen exponencialmente al igual que las técnicas disponibles, el trabajo permanente es identificar, proponer y analizar la eficiencia de las técnicas de optimización (nuevas o híbridas).
En este trabajo se analizaron restricciones de flujo de potencia, límites de generación y número de líneas por circuito; sin embargo, como trabajo futuro, se deben incluir restricciones asociadas al valor de la capacidad de las fuentes de suministro, niveles de estabilidad, adquisición de reservas, comportamiento del almacenamiento y la integración de otros sectores energéticos.