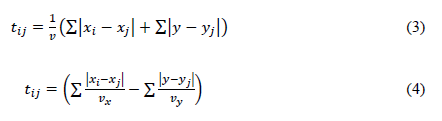1. INTRODUCTION
According to Hernández-Santibáñez et al. (2017) and Solarte et al. (2018), the facility layout problem (FLP) aims to obtain an optimal design for the allocation and flexible configuration of available machines, equipment, resources, and physical space in order to facilitate the movement and handling of material, as well as to allow plants to have optimized performance and production flow, i.e., with respect to a minimum production cost and total time. Traditionally, the study of such problems regarding distribution, spatial flow, and optimization has been addressed via dynamic programming techniques and combinatorial optimization, as per Jara-Estupiñán et al. (2020) and Dey (2020).
In this study, the FA is applied to such problems. This algorithm is inspired by the intermittent and rhythmic behavior of fireflies, which are winged insects capable of producing flashes of light to attract possible prey or companions. In FA applications, an initial population of fireflies must be configured at random node locations defined as a search space, where the fireflies represent a feasible solution. Each firefly’s flashing light intensity is the way to evaluate the target function to be optimized, as reported by Yang (2013).
This algorithm was introduced in 2009 by Xin-She Yang, who was inspired by the behavior and characteristics of fireflies such as their flickering. He established three essential rules:
Each firefly is configured to be attracted to the others regardless of its gender. Brightness is equivalent to the proportional degree of attraction. For each two blinking fireflies, the one with the lower brightness will follow to the brighter one. The attraction degree is directly related to the brightness, depends directly on the objective function, and decreases with increasing distance. If no particular firefly is brighter, they all will move randomly.
The brightness of a firefly is affected or determined by the objective function.
The layout optimization problem is similar to that of the traveling salesman problem (TSP): symmetric, uni-objective and Euclidean, according to González and Patle et al. (2018) and Trachanatzi et al. (2020). Configuring the layout of a plant is like outlining a movement in the XY plane. The total travel time can be determined as the time it takes to go through the process flow path plus the time at each station, as expressed in Equation (1):
where n is the quantity of workstations, tm the operation time per station, and t(x, y) the time it takes to follow the process flow path on the layout. The objective function is to optimize the time it takes to follow the process throughout the layout t(x, y), thus optimizing the cost of operation (Saraei et al., 2015; Hernández-Santibáñez et al., 2017). Here, the distance between the workstations i and j of the layout is considered to be rectilinear and corresponds to the Euclidean distance of the two points with coordinates (x i , y i ) and (x j , y j ). It can be calculated via Equation (2):
The equation to calculate the process flow on the layout plane XY (i.e., moving from point i to point j) implies a problem similar to that of the traveling agent. Therefore, the distance of the route can be calculated via Equations (3) and (4):
where v x and v y correspond to the process flow displacement speeds in x and y, respectively. This problem is simplified: v x and v y have the same value, so v x = v y = v.
2. METHODOLOGY
This paper applies the FA as a solving tool for combinatorial optimization problems such as the facility layout distribution problem in an industrial manufacturing plant. To this effect, many optimization algorithms have been proposed (Yang, 2013;; Łukasik & Żak, 2009). In this case, optimization can be carried out while considering the following requirements:
Minimizing material handling and the total distance between machines and layout stations.
Minimizing material flow.
Minimizing the total distance traveled by the material.
2.1. Firefly algorithm
In the FA discretization proposed by Jati (2011), a firefly represents a possible trajectory or path that gives an approximation to the optimal solution of the TSP, which is made up of a number of points or cities to be visited according to an order established by the fireflies’ movements. In the TSP, the function to be minimized is the length of the layout flow. Therefore, the brightest firefly is the one with the shortest path length, taking the Euclidean distance between all the layout points or nodes, in line with Wu et al. (2020), Kumar and Kumar (2018), and Saraei et al. (2015).
From the layout map containing the (x, y) coordinates corresponding to the location of each of the nodes or workstations distributed across the plant, the paths between nodes are defined, which conform a set of initial solutions that fireflies must optimize in each cycle (Yang & He, 2013).
The FA was initially implemented in continuous optimization applications such as the traveling agent problem, and later as a discretized way to solve permutation problems such as the one in this study case. The FA could be implemented in the optimization of maximization problems, taking the initial solution as a distance function xi, xj, according to the TSP model (Quiroga et al., 2015). According to Kumbharana and Pandey (2013), firefly movements must be redefined as the search space Sn, which includes all possible permutations {1, 2, …, n}. Firefly brightness I in each position x could be defined as I(x). Light intensity I(r) as seen by the other fireflies in the distance function r{ij} has an impact on the degree of attraction β. The light intensity changes according to the inverse square law equation (5), where the light source intensity is Is:
By taking a constant light absorption medium γ, the light intensity only changes as a distance function, as shown in Equation (6), where I 0 is the initial light intensity:
Avoiding singularity at r = 0 in
 , Equation (7) is as follows:
, Equation (7) is as follows:
By taking a degree of attraction β, Equation (8) is obtained:
where β 0 denotes the maximum degree of attraction when r = 0.
The distance formula at firefly positions (x i , x j ) is applied as defined by Equation (9):
Finally, the position of each firefly i can be determined via Equation (10):
which presents two terms. In the first one, position ij of each firefly is indicated, and, in the second one, a random value is generated to arbitrarily adjust the displacement, where a smooth factor constant α and the random function are introduced.
Objective function
Each initialized path should be evaluated by an objective function with the purpose of determining its quality rate. This comprises the evaluation of the sum of each of the distances between nodes in the path in order to determine the best sequences by taking the Euclidean distance objective function, as reported by Obando-Solano et al. (2016) and Ramírez-Ramírez et al. (2016). Thus, the sum of the distance between the current node (x i , y i) and the next node (x (i+1) , y (i+1) ), including all nodes or workstations in the layout, yields the total length of the path in Equation (11):
Path evaluation
The cost can be represented by the flow and distance matrix through Equation (12):
where d ij corresponds to the distance between nodes -or objective function- which corresponds to the Euclidean distance between points in this case.
The algorithm uses a maximum number of iterations as a stopping criterion. Once this value is reached, the process ends. However, not all paths can ensure that this solution is reached, but they can achieve an optimized one.
RESULTS
The experimental testing of the FA in the facility layout optimization problem was conducted in MATLAB, version 2020, running on a computer with an Intel CORE i7 and 8 GB RAM.
First, an initial solution is generated at random by each firefly. By taking initial values for parameters such as light intensity i, the initial degree of attraction 𝛽0 and 𝛾 are defined. Thus every firefly finds the brightest one. If the brightness of one firefly is lower than that of the other, it will move to the next brightest one. When a firefly moves along a path, its degree of attraction and its light intensity decreases, the best firefly is chosen as the initial solution for the next iteration based on the objective function. This condition is maintained until the end of iteration cycles is reached. Dhillon and Goyal (2013) propose an FA pseudo-code as follows:
Begin Initialize parameters: fireflies population n, objective function, maximum number of iterations, coefficients, 𝛼, 𝛽,𝛾, and initialization of fireflies x i, with n initial solutions and firefly light intensity Ii as a function of position x i, calculated by the objective function f(x i ).
While k i < Maximum Number of Iterations
for k i = 1 to n (Firefly Layout),
for k j = 1 to n (Firefly Layout),
If (Ij> Ii) moves from i to j;
Determine the degree of attraction reached as a function of distance r according to Equation (13):
Calculate new solutions and update the light intensity.
End End
End
Select the best solution.
End
Determine the firefly with the highest light intensity.
End
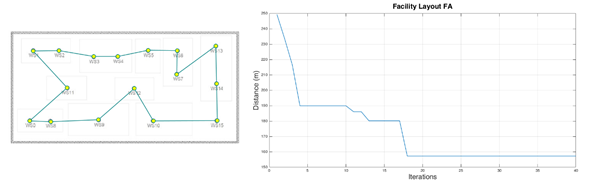
Figure 1 shows layout 1 of a mechanical factory with 15 workstations or nodes, where the path is optimized across a 124 x 60 m area. The workstations are also indicated. The previously proposed algorithm was implemented as a MATLAB script. The location coordinates (x, y) of each station were entered as vectors (x, y) in the software.
The plant layout path covers an initial distance of 283,34 m (Figure 2).
The assumption upon which the simulation was developed was established upon the following considerations. The algorithm ends when 50 iterations are performed. The minimum number of fireflies should be at least equal to the number of nodes or workstations, which was 100 in this case. The brightness function of the FA was set at m = 2. The weight parameters information at start were established arbitrarily: 𝛼 = 0,5, 𝛽 = 0,1, 𝛾 = 2, and 𝛽0 = = 10. The number of best solutions groups was assumed to be equal to 25% of the number of fireflies.
To determine the value of the absorptivity coefficient, the attractiveness function was estimated by varying the distance r ij and keeping 𝛽0 = 10. This value of β was chosen arbitrarily, although, during the experimentation phase, it was observed that a very large value of β drastically increases the simulation time and a very small value reduces the possibility of achieving an optimal solution. In the discretion of a firefly, movements are performed by permutating the visit sequence as a subset of the workstation nodes chosen at random by means of the random function, which in turn assume random positions (i, j); they are a subset that will be reordered. The probability that firefly i or j is permutated or moved more times is given by the brightness and the distance between fireflies. In this way, the solutions that give off less light are brought closer to those with a higher brightness.
A path is assigned to each workstation from i to j until all the nodes in the set are initialized, progressively evaluating the cost associated with each path to find the optimal value of cost or total distance in terms of the iterations performed.
A comparison was made against a conventional nearest neighbor constructive heuristic algorithm, or Local Optimization Algorithm (LOA). The results are shown in Figures 3 and 4.
After 31 iterations of the algorithm, the best solution corresponded to the combination shown in Table 1, with 156,0187 meters for the FA and 157,21 meters with 38 iterations for the LOA. Compared with the initial configuration of the path that was at a value of 283.34 meters.
Table 1 Results for facility layout 1 (LAO vs. FA)
| Local Optimization Algorithm | Firefly Algorithm | ||
|---|---|---|---|
| Iterations | Distance (m) | Iterations | Distance (m) |
| 46 | 163,8553 | 27 | 158,4811 |
| 45 | 158,2495 | 31 | 156,0187 |
| 42 | 160,3966 | 35 | 159,3212 |
| 38 | 157,2173 | 34 | 157,21737 |
Source: Authors
In order to evaluate the performance of the algorithm with a more robust test, a second layout corresponding to a food product factory with 200 workstations was considered. The results are shown in Figures 5 and 6.
The best solution corresponded to the combination shown in Table 2, with 8.096,936 m and 129 iterations for FA and 39.153,53 m and 200 iterations for the LOA. It is evident that, in the case of a plant with a higher degree of complexity, the FA algorithm performs better than the LOA, which, despite reaching 200 iterations, still fails to find an optimal minimum.
DISCUSSION
A two-dimensional FA representation was developed, and the algorithm showed a good performance in the test scenarios. It has optimal and fast convergence with a reasonable amount of running time over ten generations once the maximum light intensity is chosen as the optimal solution.
The optimized distances associated with the layout plan in these tests were 156,0187 and 8.096,936 m, depending on the ability to optimize time, flows, and the handling of materials, among many other aspects, until a finished product is achieved. Under that premise, the scope of the results evidenced a final strategy for saving money, but also for optimizing the material flow.
The results achieved for layout 1 by the developed FA algorithm show a similar performance to that of the conventional heuristic LOA (Table 3). After the maximum number of iterations for each generation was reached in each test, the cost function was calculated in order to validate the best option.
Table 3 Best performances for facility layout 1
| Algorithm | Iterations | Distance (m) |
|---|---|---|
| LOA | 38 | 157,2173 |
| FA | 31 | 156,0187 |
Source: Authors
In the case of a more complex layout distribution, it is evident that the FA achieves a minimum optimum with fewer iterations than the LOA algorithm (Table 4).
Table 4 Best performances for facility layout 2
| Algorithm | Iterations | Distance (m) |
|---|---|---|
| LOA | 200 | 39.153,53 |
| FA | 129 | 8.096,936 |
Source: Authors
Finally, Figure 7 shows the comparison of the initial solution with respect to the optimized layout for a plant of greater complexity, which evidences how the algorithm performs the optimization task.
CONCLUSIONS
In this research, the FA was used to define a model for representing the layout of a facility. It is important to define the objective function, ensuring that the best solution for the given problem is found. This algorithm offers a better path length, similar to other heuristic algorithms. In this case, a final optimized value of 156,0187 m was obtained for a simple facility layout, as well as 8.096.936 m for a complex facility layout -much better than the conventional heuristic algorithm.
The FA works particularly well at solving combinatorial problems whose feasible solution space is too large to carry out a comprehensive search with reasonable computation times. In this case, the FA achieved a significant reduction in iteration times and speed of optimization.
The potential applications of the FA in logistic and combinatorial optimization problems, as is the case of path planning, shows good promise for facilitating decision-making.