El dengue es una enfermedad viral transmitida por la picadura del artrópodo, mosquito Aedes aegypti, con un incremento en las regiones tropicales como Asia, África, Centro y sur América 1. Anualmente se estiman para el caso del dengue entre 50-100 millones de casos y dengue hemorrágico entre 250 000 a 500 000 casos en el mundo 2. La mitad de la población del mundo vive en áreas de riesgo de infección y también en áreas populares de destinos turísticos 3, desde entonces hubo un incremento en el mundo, y este tiende a propagarse en nuevas áreas tal como las regiones de América, se cree que el dengue era una pandemia empezando desde Asia y regiones pacificas durante la segunda guerra mundial 3, ocurriendo así cambios ecológicos en el tiempo y que probablemente favorecieron el incremento en su expansión geográfica del vector y de la densidad. El alto número de individuos susceptibles (población local, soldados) y su amplio movimiento, tal vez crearon las condiciones de dispersión del virus.
No hay vacuna, aunque los ensayos clínicos van en marcha, ni ninguna otra medicación preventiva, sin embargo algunos tratamientos médicos para casos severos son efectivos, aunque el dengue sigue siendo una de las principales causas de mortalidad en niños en Tailandia y el Sureste de Asia 4. La prevención del dengue sobre el control del mosquito, aunque se está avanzando en el desarrollo de la vacuna el dengue y drogas antivirales, no tienen licencia pero están disponibles en el mercado, y una vacuna tendrá que ser tetravalente para evitar situaciones adversas de la mejora inmunológica.
En relación a los estudios de modelado, se han construido y analizado modelos matemáticos con base en sistemas de ecuaciones diferenciales ordinarias, ecuaciones diferenciales parciales, ecuaciones integro diferénciales y redes topológicas orientados a estudiar: la dinámica de transmisión del dengue clásico con población humana constante y población humana variable 4-8, la transmisión vertical en el mosquito 9, la dinámica de transmisión espacio-temporal 10, la dinámica de transmisión de los diferentes serotipos de virus 11,12, la dinámica poblacional estocástica 13,14, la dinámica de estructura poblacional 15-17, patrones espaciales 18 y el control del mosquito: utilizando el efecto de los adulticidas y larvicidas en las tasas de mortalidad constantes 19,20 y aplicando el Principio del Máximo de Pontryagin 21,22.
En algunos estudios se considera un modelo tipo SIR (susceptible, infeccioso, inmune) para la dinámica de transmisión del dengue en la población humana con una incidencia siguiendo el principio de acción de masas o la forma estándar.
La Fuerza de la Infección es un parámetro que indica una tasa de infección, lo introdujo el epidemiólogo Hugo Muench, en su obra Modelos Catalíticos en Epidemiología en el año 1959; al realizar un estudio dinámico y comparativo entre los procesos catalíticos en la Química y la Epidemiología. Desde estos estudios y por tradición se le llama: Fuerza de la Infección.
Entre otros factores relacionados con la Fuerza de la Infección están: la naturaleza del huésped, su ciclo de vida, su forma de transmisión, la virulencia y patogenicidad, el periodo infeccioso, el contagio del ambiente, conductas alimenticias, condiciones sanitarias, condiciones sociales, culturales y la densidad de población.
El Modelo
Se formula un modelo para la incidencia del dengue clásico, considerando crecimiento logístico del hospedero, mortalidad por la infección, inmunidad a uno de los serotipos del virus, tasa de ovoposición del mosquito, dependiente del tiempo y periódica, crecimiento logístico del mosquito, los estados del ciclo de vida del mosquito, tasas de mortalidad diferentes en cada estado de vida del mosquito, (Figura 1).
Las variables y parámetros del modelo son:  número promedio de personas susceptibles,
número promedio de personas susceptibles,  número promedio de personas infecciosas,
número promedio de personas infecciosas,  : número promedio de personas inmunes a un serotipo de virus del dengue,
: número promedio de personas inmunes a un serotipo de virus del dengue,  : población promedio total variable,
: población promedio total variable,  : número promedio de mosquitos no portadores del virus,
: número promedio de mosquitos no portadores del virus,  : número promedio de mosquitos portadores del virus,
: número promedio de mosquitos portadores del virus, 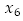 : número promedio de huevos viables,
: número promedio de huevos viables,  : número promedio de larvas,
: número promedio de larvas,  número promedio de pupas en un tiempo t, respectivamente; K
1 capacidad de carga de las personas, K
2 capacidad de carga de los mosquitos, γ tasa de crecimiento de las personas, μ tasa de muerte natural en las personas, ω tasa de muerte por la enfermedad en las personas, α tasa promedio de picadura diaria, β. fracción de picadas infectadas infligidas por los mosquitos portadores del virus,
número promedio de pupas en un tiempo t, respectivamente; K
1 capacidad de carga de las personas, K
2 capacidad de carga de los mosquitos, γ tasa de crecimiento de las personas, μ tasa de muerte natural en las personas, ω tasa de muerte por la enfermedad en las personas, α tasa promedio de picadura diaria, β. fracción de picadas infectadas infligidas por los mosquitos portadores del virus,  :, p tasa de pupas que se desarrollan a mosquito adulto, Є tasa de muerte de los mosquitos maduros por factores ambientales,
:, p tasa de pupas que se desarrollan a mosquito adulto, Є tasa de muerte de los mosquitos maduros por factores ambientales,  : población promedio de mosquitos maduros en un tiempo t,θ: tasa de recuperación de las personas infectadas, δ: tasa de huevos que se desarrollan a larvas, П tasa de eliminación de huevos por factores del ambiente, σ tasa de muerte de larvas por causas ambientales, η: tasa de muerte de pupas por causas ambientales, υ: tasa de larvas que se desarrollan a pupas, φ tasa de ovoposición dependiente del tiempo y periódica, ξ amplitud de oscilación estacional en la tasa de reproducción de los mosquitos,
: población promedio de mosquitos maduros en un tiempo t,θ: tasa de recuperación de las personas infectadas, δ: tasa de huevos que se desarrollan a larvas, П tasa de eliminación de huevos por factores del ambiente, σ tasa de muerte de larvas por causas ambientales, η: tasa de muerte de pupas por causas ambientales, υ: tasa de larvas que se desarrollan a pupas, φ tasa de ovoposición dependiente del tiempo y periódica, ξ amplitud de oscilación estacional en la tasa de reproducción de los mosquitos,  frecuencia angular del ciclo de proliferación del mosquito, correspondiente a un período de 52 semanas, ζ ángulo de fase para el ajuste del pico estacional para los mosquitos.
frecuencia angular del ciclo de proliferación del mosquito, correspondiente a un período de 52 semanas, ζ ángulo de fase para el ajuste del pico estacional para los mosquitos.
La dinámica se interpreta mediante las siguientes ecuaciones diferenciales ordinarias no lineales de acuerdo a el diagrama de compartimientos del proceso infeccioso, con 
El término  indica el crecimiento logístico de las personas, con capacidad de carga
indica el crecimiento logístico de las personas, con capacidad de carga  es la incidencia de dengue y
es la incidencia de dengue y  el número de personas susceptibles que mueren por causa natural; luego, la variación de la población susceptible en el tiempo, está dada por la ecuación diferencial ordinaria (EDO):
el número de personas susceptibles que mueren por causa natural; luego, la variación de la población susceptible en el tiempo, está dada por la ecuación diferencial ordinaria (EDO):
La variación de la población infecciosa, se interpreta mediante la EDO:
 indica el flujo de personas que mueren de forma natural, personas que mueren por la enfermedad y personas que adquieren inmunidad a un serotipo de virus de dengue.
indica el flujo de personas que mueren de forma natural, personas que mueren por la enfermedad y personas que adquieren inmunidad a un serotipo de virus de dengue.
El término  expresa el número de personas inmunes a un serotipo de virus que mueren de forma natural, la variación de dicha población está dada por la ecuación diferencial:
expresa el número de personas inmunes a un serotipo de virus que mueren de forma natural, la variación de dicha población está dada por la ecuación diferencial:
El cambio en el tiempo de la población de mosquitos no portadores del virus, está dada por el flujo de mosquitos que entran,  , menos la incidencia de mosquitos portadores del virus
, menos la incidencia de mosquitos portadores del virus  , menos el flujo de mosquitos no portadores del virus que mueren de forma natural,
, menos el flujo de mosquitos no portadores del virus que mueren de forma natural, 
De manera similar, el cambio en el tiempo de la población de mosquitos portadores del virus, se interpreta mediante la EDO:
donde,  indica el flujo de mosquitos portadores del virus que mueren de manera natural. La EDO,
indica el flujo de mosquitos portadores del virus que mueren de manera natural. La EDO,
representa la variación de huevos viables con respecto al tiempo, dada el flujo de crecimiento logístico  con tasa de ovoposición periódica
con tasa de ovoposición periódica  y capacidad de carga de los mosquitos K2, menos el flujo de huevos no viables por condiciones naturales y el flujo de huevos viables que evolucionan a larvas,
y capacidad de carga de los mosquitos K2, menos el flujo de huevos no viables por condiciones naturales y el flujo de huevos viables que evolucionan a larvas, 
Esta ecuación diferencial indica la variación de la población de larvas en el tiempo, donde,  indica el flujo de larvas que mueren por causas naturales y que se desarrollan y pasan al estado de pupas.
indica el flujo de larvas que mueren por causas naturales y que se desarrollan y pasan al estado de pupas.
En esta ecuación diferencial  indica la población de pupas que mueren por causas naturales y que se desarrollan al estado de mosquito adulto.
indica la población de pupas que mueren por causas naturales y que se desarrollan al estado de mosquito adulto.
En la EDO (9), se observa el cambio de la población total humana con respecto al tiempo, dado, por un flujo de crecimiento logístico  , menos un flujo del total de personas que mueren por causa natural µN y el flujo de personas infecciosas que mueren a causa de la enfermedad
, menos un flujo del total de personas que mueren por causa natural µN y el flujo de personas infecciosas que mueren a causa de la enfermedad .
.
De forma similar, esta ecuación diferencial, representa el cambio de la población total de mosquitos con respecto al tiempo, donde, ϵM es el flujo de mosquitos adultos que mueren por causas naturales. Se considera la función periódica,
con condiciones iniciales
y los parámetros del modelo son positivos.
Se calcula la fuerza de la infección, es decir los nuevos casos por unidad de tiempo, usando redes libres de escala:
Donde α es la tasa de picadura diaria del mosquito; β es la proporción de picadura efectiva del mosquito en el ser humano, S M y I M son el número de mosquitos susceptibles e infectados respectivamente, y N H y N M son el número total de humanos y mosquitos respectivamente.
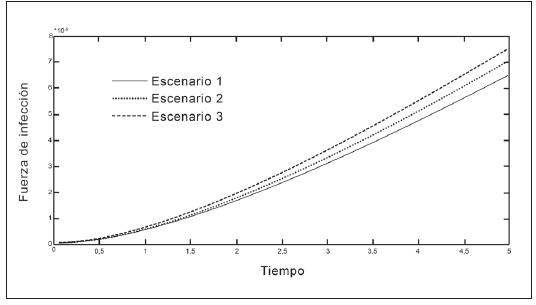
En las Tablas 1 y 2 se presentan los valores de los parámetros que intervienen en la fuerza de infección. En las Figuras 2 a 5 se observa que la fuerza de infección aumenta de acuerdo a los diferentes escenarios y en el tiempo, es decir, la tasa de nuevos casos crece, mostrando la necesidad de prevención en las personas, mediante el uso de telas metálicas, mosquiteros, repelentes, ropa adecuada entre otras medidas; control químico como larvicidas y adulticidas contra el vector, como también la eliminación de criaderos que interrumpan su ciclo de vida. También es importante tomar medidas con las personas infectadas, debido a que si tratan de manera adecuada, se reduce la transmisión del virus.