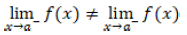Introducción
Algunos resultados de investigaciones recientes han señalado la transición de las notaciones matemáticas tradicionales en papel a las notaciones en pantalla (incluyendo símbolos algebraicos, gráficos, tablas y figuras geométricas) con cierto efecto dramático (Ioannou et al., 2017; Sangwin y Köcher, 2016). A diferencia del uso del papel y el lápiz, que solo admite notaciones estáticas y aisladas, el de computadores admite notaciones dinámicas vinculantes con varias ventajas útiles (Potkonjak et al., 2016). El uso adecuado de las TIC permite a los estudiantes tener la libertad de elegir su propio tiempo, lugar y ritmo de estudio. Los materiales de aprendizaje se mejoran con diversos medios como el sonido, la narración, el video, la animación, los gráficos, etc.; lo que proporciona a los estudiantes posibilidades que se adaptan a sus diferentes estilos y ritmos de formación. A través de una planificación y una implementación adecuada, la educación apoyada por TIC puede promover la adquisición de conocimientos y habilidades como la creatividad y el pensamiento crítico (Koh et al., 2015). De este modo, las nuevas formas de aprender y enseñar asientan la transformación de una pedagogía centrada en el profesor a otra centrada en el estudiante (Feist y Reid, 2018).
En el campo de la educación matemática la tecnología puede reorientar el esfuerzo dedicado a la ejecución de operaciones y dirigir la atención de los estudiantes hacia el contexto que rodea los problemas en matemáticas. La tecnología puede favorecer las representaciones matemáticas, de manera que los estudiantes puedan resignificar sus conceptos (Stacey y Wiliam, 2012). Los recursos tecnológicos disponibles, como los sistemas de álgebra computacional, el software de geometría interactiva y los applets, constituyen nuevos recursos didácticos para redefinir la enseñanza de las matemáticas y, de este modo, desarrollar la resolución de problemas y la toma de decisiones entre los estudiantes, a partir de una reconceptualización que podría conducir a estrategias eficaces para mejorar el apoyo en el uso de las TIC por parte de los profesores en el aula (Sinclair, 2020). Y en esta reconceptualización el profesor de matemáticas enfrenta el desafío de facilitar el aprendizaje proporcionando a los estudiantes acceso a la tecnología de enseñanza que incluye los dispositivos móviles, el software especializado y la conexión a internet. De ahí que se establezcan nuevas formas de enseñar y, por supuesto, de aprender en las cuales los estudiantes logren incorporar las TIC con el propósito de redefinir el alcance de sus resultados de aprendizaje.
En este contexto, aparece el aprendizaje móvil (mobile learning o m-learning) como una oportunidad de aprender a través de contextos diversos e interacciones múltiples a través de dispositivos móviles (Ballesteros et al., 2020). El m-learning constituye una etapa renovada del aprendizaje mediado por la tecnología en la que los estudiantes pueden acceder a la información, aprender de forma individual o grupal, en el aula tradicional de clase y fuera de ella, utilizando como herramienta de apoyo sus dispositivos móviles personales (Al-Emran et al., 2018). Se trata, en todo caso, de una concepción tecnocéntrica que enriquece el quehacer pedagógico centrada en el estudiante y que, al mismo tiempo, debe desarrollar aspectos motivacionales y afectivos como el control, la propiedad, la diversión, la comunicación, el aprendizaje en el entorno y la continuidad entre contextos (Jeno et al., 2019). El m-learning involucra los intereses de los estudiantes que se identifican como parte de una comunidad digital que utiliza, a diario, artefactos tecnológicos para dinamizar su cotidianidad. Así pues, el profesor de matemáticas se ve abocado a integrar los dispositivos móviles al aula de clase o continuar negando una realidad plural abiertamente tecnológica y que distancia a la escuela de los sucesos que acontecen en la sociedad, con el mecanismo de la prohibición unilateral de estos dispositivos.
Con este escenario y con reconocimiento consciente de las necesidades de aprendizaje de los estudiantes de ingeniería de la Fundación Universitaria Los Libertadores, se propuso la siguiente pregunta de investigación: ¿qué influencia tiene en el desempeño académico y el desarrollo actitudinal de los estudiantes el uso de la aplicación móvil Calculadora Gráfica de GeoGebra (en adelante ACCG) para el aprendizaje de la noción de límite? Para responder a esta pregunta se planteó como objetivo general la necesidad de describir los efectos y las experiencias de la incorporación de la ACCG para el aprendizaje de la noción de límite con estudiantes de Ingeniería Aeronáutica a partir de la integración de dispositivos móviles al aula de clase y, de este modo, validar la hipótesis asociada a una influencia positiva del uso de esta aplicación móvil en el aprendizaje de esta noción.
Revisión de la literatura
La revisión literaria para esta investigación se realizó con dos ejes vertebradores: el aprendizaje móvil y el software de geometría dinámica.
Aprendizaje móvil o m-learning
Con la creciente cobertura de las redes móviles y el aumento en el uso de dispositivos como teléfonos inteligentes, tabletas o iPads, que son compañeros constantes para muchas personas, la industria móvil ha experimentado un rápido crecimiento tanto en los países desarrollados como en vías de desarrollo. Con una tasa de propiedad personal alta y en constante aumento, los servicios de aprendizaje pueden desempeñar un papel cada vez más importante y eficaz en la educación. En otras palabras, la tecnología de comunicación móvil se ha infiltrado en la vida cotidiana en todo el mundo (Hao et al., 2017). En años recientes han aparecido nuevos términos como aprendizaje electrónico y aprendizaje móvil. Este último se ha posicionado como la adquisición de conocimientos, habilidades y actitudes mediante la utilización de tecnologías móviles tales como teléfonos inteligentes, tabletas, iPads, etc. (Hamidi y Chavoshi, 2018). El m-learning permite el acceso continuo al conocimiento en cualquier momento y lugar. Mediante los dispositivos móviles se crean facilidades especiales como el envío y el almacenamiento del contenido de aprendizaje, al igual que se generan otros métodos de instrucción y un aumento de los recursos de enseñanza y de las interacciones bidireccionales; además de aportar a la flexibilidad de aprendizaje al ser decisión del estudiante el momento y lugar que desee disponer (Tang y Hem, 2017).
Todos los enfoques de enseñanza que se apoyan en las TIC se han desarrollado con la intención de mejorar la calidad de la enseñanza y promover el acceso a distintos recursos para aprender (Prada y Hernández, 2016). Aunque el aprendizaje móvil ha estado presente en la educación superior durante varios años, sigue configurándose como una tecnología emergente y aún existen preguntas sobre su despliegue. ¿Será que los estudiantes preferirán los dispositivos móviles y tendrán un mejor rendimiento si los usan en lugar de un computador?, ¿cómo se integra mejor el aprendizaje móvil en un contexto de aprendizaje?, ¿el aprendizaje móvil simplemente proporcionará otro punto de acceso a la información y la comunicación, o surgirá una pedagogía transformadora? (Hao et al., 2017). Desde distintas orillas se han abordado estas inquietudes y se han desarrollado experimentos de enseñanza que enfrentan el rendimiento logrado con dispositivos móviles y el rendimiento alcanzado con otros recursos, tal vez, tradicionales (Martin y Ertzberger, 2013; Tossell et al., 2015; Wong et al., 2015, Saavedra, 2016).
Software de geometría dinámica
El software de geometría dinámica (en adelante SGD) ha estado presente durante más de 30 años, llegando a la mayoría de las aulas de todo el mundo y convirtiéndose en un componente insustituible de la educación matemática. Desde el principio las herramientas de los SGD se han diseñado alrededor de un escenario central donde el usuario define varios puntos móviles y, a través de ellos, construye nuevos puntos y otros objetos geométricos que dependen de ellos para lograr su manipulación y explorar sus rutinas de variación (Plaza, 2016; Selaković et al., 2019). A continuación, en la tabla 1, se relacionan las principales referencias bibliográficas que documentan el avance del SGD a lo largo del tiempo:
La característica de arrastre es simple pero muy atractiva y efectiva en la educación matemática; en lugar de explorar las figuras geométricas estáticas los estudiantes pueden explorar figuras estrechamente relacionadas arrastrando algunos puntos libres para poder observar propiedades o invariantes sobre ellas (Hussin et al., 2018).
Metodología
Para el desarrollo de este proyecto de investigación se diseñaron dos unidades didácticas. Ambas tuvieron como objetivo central aproximar a los estudiantes a la noción de límite. La primera se centró en recursos didácticos tradicionales como la calculadora científica, lápiz y papel. La segunda fue diseñada para facilitar la interacción con la ACCG en dispositivos móviles a partir de tres actividades de aprendizaje y dos actividades de evaluación, un pretest y un postest. En comparación con otras herramientas de geometría dinámica, se optó por la ACCG porque combina el álgebra y la geometría dinámica con la función de arrastre de puntos construidos para generar nuevas interacciones con objetos matemáticos, de modo que se puede representar una amplia variedad de funciones (Hohenwarter y Fuchs, 2004).
Construcción geométrica dinámica
El objetivo de esta construcción es generar la noción visual del límite:
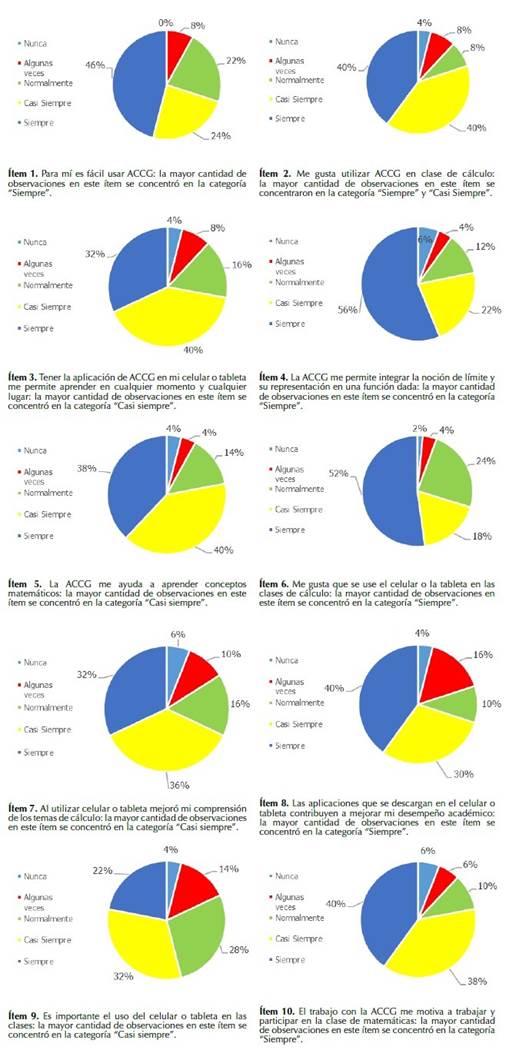
A través de herramientas de arrastre mediante la interacción con dispositivos móviles y argumentar en qué condiciones dicho límite existe. Se definen la función
 junto con dos puntos móviles
junto con dos puntos móviles
 y
y
 sobre el eje de las abscisas, que pueden cambiar de posición por medio de arrastre cuando se manipulan dos deslizadores, hecho que permite ver la tendencia de
sobre el eje de las abscisas, que pueden cambiar de posición por medio de arrastre cuando se manipulan dos deslizadores, hecho que permite ver la tendencia de
 al valor de
al valor de
 tanto por izquierda
tanto por izquierda
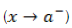 como por derecha
como por derecha
 (figura 1).
(figura 1).

Fuente: elaboración propia de los autores
Figura 1 Puntos móviles A y X que por medio de arrastre permiten ver la tendencia de x al valor de a.
Es importante resaltar que la manipulación de estos dos puntos es el factor que hace dinámica la construcción.
Luego, haciendo uso de las herramientas que ofrece la ACCG tales como funciones, puntos de intersección, rectas y vectores se crea un ambiente dinámico donde se ve la tendencia de
 cuando
cuando
 (figura 2).
(figura 2).
Con esta construcción geométrica dinámica los estudiantes pudieron observar cuál era la tendencia de la función
 cuando, a través de arrastre, aproximaban el valor de
cuando, a través de arrastre, aproximaban el valor de
 al valor de
al valor de
 .
.
Primera actividad
Con esta actividad se buscó que los estudiantes pudieran explorar el límite
 cuando la función
cuando la función
 es continua en
es continua en
 . En la figura 3 se muestra un ejemplo desarrollado durante el tratamiento experimental donde se observó el
. En la figura 3 se muestra un ejemplo desarrollado durante el tratamiento experimental donde se observó el
 .
.

Fuente: elaboración propia de los autores
Figura 3 Ejemplo de la interacción de los estudiantes con la ACCG para la noción de límite en puntos de continuidad.
Sin embargo, se trabajaron más ejemplos con funciones racionales, exponenciales, trigonométricas y composiciones en puntos del dominio donde se sabe que son continuas. Esto permitió a los estudiantes ver que si la función
 es continua en
es continua en
 , entonces:
, entonces:
Segunda actividad
En esta actividad se abordó el concepto de límite
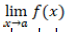 para valores
para valores
 del dominio de
del dominio de
 donde la función presenta discontinuidades de salto. Para esto se estudiaron funciones a trozos como:
donde la función presenta discontinuidades de salto. Para esto se estudiaron funciones a trozos como:
Observando a través de arrastre la tendencia de
 cuando
cuando
 por izquierda y por derecha de
por izquierda y por derecha de
 (figura 4).
(figura 4).

Fuente: elaboración propia de los autores
Figura 4 Análisis de la no existencia de
 mediante la observación de límites laterales en dispositivos móviles con la ACCG.
mediante la observación de límites laterales en dispositivos móviles con la ACCG.
También se estudiaron otras funciones particulares como la función parte entera en valores enteros de
 (figura 5).
(figura 5).

Fuente: elaboración propia de los autores
Figura 5 Análisis de la no existencia de
 mediante límites laterales en dispositivos móviles con la ACCG.
mediante límites laterales en dispositivos móviles con la ACCG.
El trabajo con este tipo de funciones y la exploración de las mismas a través del uso de las herramientas de arrastre que ofrece la ACCG permitió a los estudiantes interactuar con valores cercanos a para ver que si la función
 tiene una discontinuidad de salto en
tiene una discontinuidad de salto en
 , entonces:
, entonces:
Tercera actividad
En esta actividad se trabajaron límites infinitos. Para ello se consideraron funciones racionales como:
Y mediante herramientas de arrastre se examinaron límites como por ejemplo
 (figura 6).
(figura 6).

Fuente: elaboración propia de los autores
Figura 6 Observación de límites laterales que dan infinito mediante arrastre con la ACCG.
Esta actividad permitió que los estudiantes observaran mediante arrastre que en funciones que tienen discontinuidades infinitas en
 cuanto más se aproxima el valor de
cuanto más se aproxima el valor de
 tanto por la izquierda como por la derecha de
tanto por la izquierda como por la derecha de
 , los valores de
, los valores de
 decrecen o crecen sin cota. Los ejercicios en esta actividad consistieron en explorar límites de diferentes funciones con límites infinitos, por ejemplo
decrecen o crecen sin cota. Los ejercicios en esta actividad consistieron en explorar límites de diferentes funciones con límites infinitos, por ejemplo
 .
.
Resultados
Para el análisis de resultados se tomó como variable de interés para el respectivo análisis el puntaje del postest y la presencia (o no) del pretest. La figura 7 presenta la distribución observada de los cuatro grupos y la relación entre ellos en términos de la presencia o ausencia del pretest y de la intervención.

Fuente: elaboración propia de los autores
Figura 7 Distribución observada de los resultados en los cuatro grupos considerados.
En este punto, y desde una perspectiva enteramente descriptiva y exploratoria, es posible hacer los siguientes comentarios:
De manera visual puede conjeturarse que la intervención tiene un efecto positivo en los grupos, pues los grupos GE1 y GE2 lograron mejores resultados que los grupos que no tuvieron la intervención con la herramienta propuesta.
Se considera que se debe destacar la diferencia en el efecto del pretest (presentarlo o no) en la calificación obtenida en postest en los grupos control (no recibieron la intervención). Es decir, la presencia del pretest afecta la calificación en el postest.
Podría conjeturarse inicialmente que sí existe un efecto del pretest en el postest en los grupos que sí recibieron la intervención, pues el grupo GE2 (que no presentó pretest y tuvo la intervención mediada por la aplicación móvil) tuvo un mejor desempeño que el grupo GE1 (que sí presentó pretest y también contó con intervención mediada por dicha aplicación).
Para el análisis inferencial de la información recolectada se procedió de acuerdo con Braver y Braver (1988), quienes plantean una estrategia general para el análisis de este tipo de información (cuatro grupos de Solomon). Para este caso se descarta la influencia de la interacción, con una Anova de 2×2 con interacción, por lo que es pertinente analizar los resultados con una Anova de 2×2 de efectos principales en el experimento (pretest e intervención). La implementación computacional del estudio se realizó en el paquete estadístico R (versión 3.6.0) sobre un sistema operativo Ubuntu 18.04.4 LTS.
La tabla 2 presenta el resultado obtenido para el montaje de una Anova de 2×2 con efectos fijos. La figura 8 presenta una distribución adecuada para los residuos alrededor del intervalo de confianza (en azul) del 95 % de confianza para los residuos. Además, el p-valor de la prueba de normalidad de Jarque-Bera para los residuos del mismo es 0,938, lo que permite concluir la normalidad de los mismos.
Tabla 2 Resultados de Anova de 2×2 de efectos principales sin interacciones.

Fuente: elaboración propia de los autores.

Fuente: elaboración propia de los autores
Figura 8 Distribución observada de los resultados en los cuatro grupos considerados.
La figura 9 presenta una buena distribución para los valores observados respecto a sus valores estimados, lo cual muestra que no existe evidencia de desviación de alguno de los supuestos del modelo general. De esta manera, con un nivel de significancia del 5 %, hay evidencia relevante para afirmar que el modelo es válido.

Fuente: elaboración propia de los autores
Figura 9 Residuos versus valores ajustados para el modelo considerado.
Según la información de la figura 9, y asumiendo un nivel de significancia del 5 %, se infiere la existencia de evidencia estadísticamente significativa para concluir que la intervención mediada por la aplicación móvil tiene efecto en los resultados del postest. De la misma manera, se concluye también que existe evidencia estadísticamente significativa a favor de la hipótesis de que el pretest sí influye en los resultados del postest. En otras palabras, la existencia (más allá de la calificación) de la prueba de entrada tiene un efecto condicionador sobre los estudiantes durante su proceso de aprendizaje mediado por la ACCG sobre el estudio de la noción de límite para la prueba de salida. Es decir, la experiencia del pretest condiciona el resultado del postest, impidiendo así que la obtención de resultados sea clara y únicamente atribuible al tipo de intervención. De esta forma, además de resaltar el uso de las tecnologías en el aula como medio para facilitar el aprendizaje del cálculo, se debe destacar la importancia del pretest en el montaje de experimentos para verificar la eficacia de una estrategia didáctica particular.
Por otra parte, en la figura 10 se presenta el análisis de la encuesta actitudinal que se aplicó a los 66 estudiantes de los grupos experimentales, en la cual se puede evidenciar una aceptación importante de la ACCG como recurso didáctico para el aprendizaje del concepto de límite.
De acuerdo con Hamidi y Chavoshi (2018), también se observa a partir de los resultados de esta investigación que el aprendizaje móvil podría ser una de las tecnologías educativas prometedoras para el desarrollo en los entornos educativos. En coherencia con Maulyda et al. (2019), se encontró que los estudiantes lograron entender qué sucede al variar ciertos parámetros de las funciones analizadas así como los desplazamientos que sufren y cómo lograron comprender la noción de límite mediante la interacción con la ACCG a través de acercamientos por izquierda y derecha a un determinado valor con el uso de herramientas de arrastre.
Conclusiones
Los resultados obtenidos en este proyecto de investigación refuerzan los hallazgos de Al-Emran et al. (2016), que reconocen la emergencia de tecnologías revolucionarias que han alcanzado un impacto significativo en la sociedad a través de la tecnología educativa. A renglón seguido, el uso de GeoGebra produce efectos de gran valor en los procesos de enseñanza y aprendizaje de las matemáticas en educación superior; una elección apropiada de contenidos reforzados con GeoGebra y el rediseño de actividades puede conducir a los estudiantes hacia el aprendizaje de la noción de límite y, por lo tanto, a mejorar su rendimiento académico en cursos posteriores de cálculo para ingeniería en concordancia con los hallazgos de Wassie y Zergaw (2019).
En concordancia con Willemse et al. (2019), los resultados presentados en este artículo permiten considerar los dispositivos móviles como herramientas útiles en los procesos de aprendizaje en el aula y vincularlos no debe asociarse con la presencia de distractores, sino que conjugados con aplicaciones como la ACCG pueden lograr efectos positivos sobre los procesos de aprendizaje de las matemáticas. También, en sintonía con Alwraikat y Al Tokhaim (2014) y Alwraikat (2017), mediante el análisis de evidencias estadísticas significativas las actitudes de los estudiantes deben ser positivas hacia el m-learning para que este pueda generar resultados favorables. Tomar la decisión de diseñar construcciones geométricas dinámicas desde dispositivos móviles y llevarlas al aula constituye un cambio en la educación matemática congruente con el cambio que ha tenido la sociedad cada vez más permeada por el uso de la tecnología.