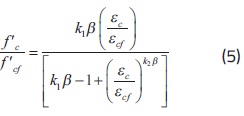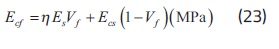COMPORTAMIENTO DEL CONCRETO REFORZADO CON FIBRAS DE ACERO ZP-306 SOMETIDO A ESFUERZOS DE COMPRESIÓN

BEHAVIOR OF ZP-306 STEEL FIBER REINFORCED CONCRETE SUBJECTED TO COMPRESSIVE STRESSES

Lina P. Gallo-Arciniegas
Auxiliar de Investigación, Programa de Ingeniería Civil,
Universidad Militar Nueva Granada, UMNG, Bogotá, Colombia
linin_25@hotmail.com

Giovanni González Peñuela
Esp., Profesor Investigador, Programade Ingeniería Civil,
Universidad Militar Nueva Granada, UMNG, Bogotá, Colombia
gonzalez.giovanni@gmail.com

Julián Carrillo León
Ph.D., Profesor Investigador, Programa de Ingeniería Civil,
Universidad Militar Nueva Granada, UMNG, Bogotá, Colombia
wjcarrillo@gmail.com

Fecha de recepción: 22 de enero de 2013 Fecha de aprobación: 23 de mayo de 2013

RESUMEN

En Colombia, el uso del concreto reforzado con fibras de acero (CRFA) es muy limitado, debido a que en el país no existe suficiente evidencia experimental y requisitos reglamentarios al respecto. En el artículo se presentan los resultados de una investigación experimental y analítica sobre el comportamiento del CRFA elaborado con fibras ZP- 306, sometidas a esfuerzos de compresión. El estudio involucra la revisión y discusión de los modelos disponibles en la literatura, así como un programa experimental que incluye el ensayo de 48 especímenes. A partir de un análisis de regresión de los datos medidos, se proponen ecuaciones para estimar las principales propiedades mecánicas del CRFA, tales como resistencia a compresión, módulo de elasticidad y relación de Poisson. Las ecuaciones correlacionan las propiedades mecánicas con las principales características de las fibras de acero, tales como dosificación y relación de aspecto.

Palabras clave: Concreto reforzado con fibras de acero, compresión, módulo de elasticidad, relación de Poisson, contenido de fibras.

ABSTRACT

In Colombia, the use of steel fiber reinforced concrete (SFRC) is lacking because there are not enough experimental evidence and regulatory requirements on that subject in the country. This paper shows the results of an experimental and analytical researchon behavior of SFRC made of ZP-306 fibers, subjected to compressive stresses. The study involves the review and discussion of models available in the literature, as well as anexperimental program that included the test of 48 specimens. From a regression analysis of the measured data, equations are proposed to estimate the main mechanical properties of the SFRC, such as compressive strength, modulus of elasticity and Poisson's ratio. The equations correlate the mechanical properties with the main characteristics of steel fibers, such as content and aspect ratio.

Key words: Steel fiber reinforced concrete, compression, modulus of elasticity, Poisson's ratio, fiber content.

INTRODUCCIÓN

El concreto reforzado con fibras de acero (CRFA) ha evolucionado desde un material de construcción hasta una alternativa usada para mejorar tanto el concreto convencional simple, como el concreto reforzado con barras o malla electro soldada. Es evidente que el comportamiento a tensión del concreto simple (CS) es deficiente, lo cual se podría mejorar con la adición de fibras al concreto. En general, las fibras controlan la fisuración y mejoran la tenacidad del concreto [1, 2].

Varias investigaciones y proyectos prácticos se han llevado a cabo con éxito para caracterizar y estudiar el comportamiento del CRFA. A pesar de esta amplia experiencia, muchos diseñadores no conocen el comportamiento y las ventajas del CRFA. Una de las principales causas de la poca utilización del CRFA en las construcciones de Colombia, ha sido la ausencia de recomendaciones prácticas para estimar el comportamiento del CRFA. Aunque el Reglamento Colombiano de Construcción Sismo Resistente (NSR-10) permite el uso de fibras de acero en el concreto para resistir cortante en vigas, NSR-10 excluye su uso en otros elementos tales como muros de concreto. Adicionalmente, en NSR-10 no se indican ecuaciones para estimar las propiedades mecánicas del CRFA.

El uso de fibras de acero en el concreto contribuye a mejorar el proceso constructivo y el comportamiento sísmico de elementos estructurales, lo que redunda en viviendas más económicas y seguras. Por tal motivo, en este artículo se presentan los resultados de una investigación experimental y analítica para estudiar el desempeño del CRFA elaborado con fibra ZP-306, y sometido a esfuerzos de compresión. Las propiedades que se incluyen son resistencia a compresión, módulo de elasticidad, relación de Poisson y, en general, la curva completa esfuerzo-deformación. Inicialmente, se presentan los resultados de una revisión de las metodologías propuestas en la literatura. Luego se presentan los resultados de un estudio experimental sobre 48 muestras de CRFA en forma de cilindros. Por último, se presentan recomendaciones prácticas para caracterizar el comportamiento del CRFA sometido a esfuerzos de compresión.

1. COMPORTAMIENTO DEL CRFA SOMETIDO A ESFUERZOS DE COMPRESIÓN

Las fibras de acero incrementan las propiedades a flexión, tensión, cortante, fatiga, impacto y desgaste, y controlan la fisuración del CS. Por tanto, la adición de fibras de acero promueve concretos con mejores desempeños y con mayor durabilidad. Usualmente, las fibras de acero producen ligeras modificaciones de la resistencia a compresión del concreto [3].

En la literatura se reportan diferentes modelos para predecir la curva esfuerzo-deformación del CS. Los modelos de Popovics [4], y Carreira y Chu [5] han sido la base para desarrollar modelos de predicción de la curva esfuerzo-deformación del CRFA. En la Figura 1 se muestra la curva característica esfuerzo-d eformación del CRFA, donde f’_cf es la resistencia a compresión del CRFA y ε_cf es la deformación correspondiente a f’_cf (el símbolo prima, ‘, significa que el valor es nominal).

Aunque varios modelos para CRFA se han desarrollado a partir de modelos para CS, se deben modificar las ecuaciones para incluir parámetros que consideran la influencia de las fibras sobre las propiedades de la curva de esfuerzo-deformación.

A partir de la curva esfuerzo-deformación se pueden obtener dos tipos de módulos de elasticidad; secante y tangente. El módulo secante es el más utilizado y representa el valor de la pendiente de la línea que une los puntos de la curva esfuerzo-deformación longitudinal, correspondientes a una deformación asociada al esfuerzo nulo o de 0.00005, y una deformación asociada a un determinado porcentaje del esfuerzo máximo medido en los ensayos de resistencia a compresión; usualmente el 40%. El módulo tangente se puede considerar como un módulo tangente en el origen o módulo inicial, o un módulo tangente en un punto correspondiente a un determinado esfuerzo (Ver Figura 1).

1.1 Curva esfuerzo-deformación

En esta sección, se describen y discuten los principales modelos propuestos en la literatura para predecir la curva esfuerzo-deformación del CRFA, sometido a esfuerzos de compresión.

1.1.1 Ezeldin y Balaguru

Ezeldin y Balaguru [6] estudiaron el comportamiento experimental de concretos con resistencia a compresión que varió entre 35 MPa y 85 MPa, reforzados con fibras de acero con relación de aspecto (l_f /d_f) de 60, 75 y 100, y fracción de volumen de fibras (V_f) quevarió entre 0% y 0.75%. La relación de aspecto, l_f /d_f, representa el cociente entre la longitud y el diámetro de la fibra. La fracción de volumen, V_f, se calcula como el cociente entre la dosificación de fibras, D_f, en kg/m³, y la densidad del acero, Js, la cual es igual a 7850 kg/m³ (V_f =D_f /γ_s); donde V_f se puede expresar en fracción o en porcentaje. Con base en la forma funcional de la ecuación propuesta por Carreira y Chu [5], Ezeldin y Balaguru, proponen la ecuación 1 para predecir la curva esfuerzo-deformación del CRFA.

Donde f’_c y f’_cf son las resistencias a compresión del concreto simple y del CRFA, respectivamente, ε_c es la deformación del concreto simple asociada a f’_c (en este estudio, Hc se considera igual al valor especificado en NSR-10; es decir, ε_c 0.002), y ε_cf es la deformación del CRFA asociada a f’_cf, la cual se calcula con la ecuación 2.

donde R_I es un índice de reforzamiento y se calcula con la ecuación 3.

Donde W_f es el peso de las fibras en fracción. De acuerdo con Ezeldin y Balaguru, W_f puede relacionarse, de forma aproximada, con la fracción de volumen de fibras; es decir, W_f =3.27V_f, donde V_f se expresa en fracción En la ecuación 1, β es un factor que considera la influencia de las fibras en la forma de la curva y se calcula con la ecuación 4.

1.1.2 Mansur

Mansur et al. [7] estudiaron el comportamiento experimental del CRFA con resistencia a compresión que varió entre70 MPa y 120 MPa, V_f entre 0% y 1.5%, y l_f /d_f de 60. Con base en la forma funcional de la ecuación 1, Mansur et al. propone utilizar la ecuación1 para ε_c≤ ε_cf y la ecuación 5 para ε_c> ε_cf

Donde k₁ y k₂ son parámetros para incluir la influencia de las fibras en el comportamiento del CRFA y se calculan con las ecuaciones 6 y 7, respectivamente. En todas las ecuaciones del modelo de Mansur, V_f se expresa en fracción, y f'_cf,f'_c y E_cf en MPa.

En la ecuación 5, ε_cf se calcula con la ecuación 8, y el factor β se calcula con la ecuación 9.

donde E_cf es el módulo de elasticidad tangente inicial del CRFA (Ver Figura 1) y se calcula con la ecuación 10.

1.1.3 Araujo

Araujo [8] midió la resistencia a compresión de cilindros de 100mm de diámetro y 200mm de altura, con Vf que varió entre 0.75% y 2%. Para estimar la curva esfuerzo– deformación del CRFA, Araujo adoptó las ecuaciones 5 y 9. Sin embargo, para obtener los parámetros k1 y k2, Araujo propone utilizar las ecuaciones 11 y 12, respectivamente. En todas las ecuaciones del modelo de Araujo, Vf se expresa en fracción, y f’_cf y E_cf en MPa.

Para utilizar la ecuación 5, el factor Ese calcula con la ecuación 9 y ε_cf se calcula con la ecuación 13.

En la ecuación 9, E_cf es el módulo tangente inicial y se calcula con la ecuación 14.

1.1.4 Nataraja et al.

En el programa experimental de Nataraja et al. [3,9] se utilizó CRFA con resistencia a compresión que varió entre 30 y50 MPa, V_f entre 0% y1%, y l_f /d_f entre 55 y 82. Nataraja et al. propone utilizar la ecuación 1 para estimar la curva esfuerzo-de formación. Sin embargo, los parámetros ε_cf y f’_cf se obtienen con las ecuaciones 15 y 16, respectivamente. Para V_f <1.0%, β se calcula con la ecuación 17. En las ecuaciones 15, 16 y 17, RI se calcula con la ecuación 3.

1.1.5 Oliveira et al.

En el estudio de Oliveira et al. [10] se realizaron doce mezclas de CRFA, con tres cilindros de 150mm de diámetro y 300mm de alto por cada mezcla. En el estudio se utilizó concreto con resistencia a compresión que varió entre 40 MPa y 60 MPa, V_f de 0%, 1.0% y 2.0%, y fibras con l_f /d_f de 64. El modelo analítico propuesto para predecir la curva esfuerzo-deformación se desarrolló con base en la ecuación 1, donde ε_cf y β se calculan con las ecuaciones 18 y 19, respectivamente, y V_f se expresa en fracción.

Prashant et al.

Prashant et al.[11,12] ensayaroncubos con aristas de 150mm,y cilindros de 150mm de diámetro y 300mm de altura, con cemento sin adición y con adición de 8% de humo de sílice. En el programa experimental,los valores de V_ffueron 0%, 0.5%, 1.0% y 1.5%, el diámetro de las fibras de 0.5mm, y l_f /d_f de 60. Prashant et al.Proponecalcular la resistencia a compresión del CRFApor medio de la ecuación 20, donde V_fse expresa en porcentaje.

Prashant et al. [11] proponen estimar el valor de Ecf secante con el primer punto de la línea asociado al esfuerzo nulo y el segundo punto al 45% de f’_cf, por medio de la ecuación 21. En estudios posteriores, Prashant et al. [12] proponen calcular el valor de E_cf secante con el primer punto de la línea asociado al esfuerzo nulo y el segundo punto al 45% de f’_cf, por medio de la ecuación 22.

1.2 Módulo de elasticidad

Algunos de los modelos que predicen la curva esfuerzo-deformación del CRFA, también proponen ecuaciones para predecir explícitamente E_cf, tales como Mansur et al.[7], Araujo [8] y Prashant et al. [11, 12]. A continuación se describen otros modelos que predicen exclusivamente E_cf.

1.2.1 Ponce

Ponce [13] propone calcular E_cf secante con el primer punto de la línea asociada al esfuerzo nulo y el segundo punto al 40% de f’_cf (Ver Figura 1), por medio de la ecuación 23.

donde V_f se expresa en porcentaje, n es el coeficiente de eficiencia de las fibras, el cual se puede tomar como 0.41 para todos los tipos de fibras, E_s es el módulo de elasticidad de las fibras de acero y E_cs es el módulo de elasticidad del concreto simple. De acuerdo con las secciones C.8.5.2 y C.8.5.1 de NSR-10, Es 200000 MPa, y Ecs secante con el primer punto de la línea asociado al esfuerzo nulo y el segundo punto al 45% de f’c, se calcula con la ecuación 24.

1.2.2 Mármol

Mármol [14] propone calcular E_cf secante con el primer punto de la línea asociado al esfuerzo nulo y el segundo punto al 40% de f’_cf (Ver Figura 1b), por medio de la ecuación 25.

donde V_f se expresa en porcentaje y n₀ es el factor de orientación fibras, el cual es igual a 0.41 l_f.

2. PROGRAMA EXPERIMENTAL

El programa experimental incluyó el ensayo de 48 especímenes de CRFA en forma de cilindros de 150 mm de diámetro y 300 mm de altura; 16 para CS y 32 para CRFA. Para CS, los cilindros se ensayaron a edades de 7, 14, 28 y 335 días, con el propósito de evaluar la evolución de la resistencia. Para CRFA, los cilindros se ensayaron a edad de 335 días, con el fin de caracterizar el comportamiento del CRFA sometido a esfuerzos de compresión. En el programa experimental se utilizó un tipo de fibra y tres dosificaciones, tal como se describe en la Tabla 1.

2.2 Matriz de ensayos

Los resultados de los ensayos se utilizaron para obtener índices de resistencia a compresión, módulo de elasticidad y relación de Poisson. En la Tabla 2 se indican los tipos de ensayo y la cantidad de especímenes utilizados.

2.3 Características del concreto

La resistencia nominal a compresión del concreto, f'_c, fue de 25 MPa, el tamaño máximo del agregado de 10mm y el asentamiento mínimo especificado de 180mm. El concreto fue premezclado y proporcionado por la Empresa Argos. Las fibras fueron mezcladas en sitio para obtener cada dosificación. La cantidad de fibras de la menor dosificación (25% de D_f-min = 15 kg/m3) se adicionó en el lugar de fundida de los especímenes. Cuando finalizó la elaboración de los especímenes con la primera dosificación, se adicionó al concreto la cantidad de fibras necesaria para lograr la dosificación siguiente (50% de D_f-min = 30 kg/m3 y 100% de D_f-min = 60kg/m3).

A los especímenes de concreto se les realizó un proceso de curado que consistió en el riego con agua pura, aproximadamente cada 9 horas, por dos días, y al tercer día se aplicaron dos capas de la membrana de curado antisol blanco (fabricado por Sika).

2.4 Configuración de ensayos

2.4.1 Ensayos en estado fresco

En cada dosificación se midió el asentamiento del CRFA siguiendo el procedimiento de la norma NTC 396 [15]. De acuerdo con la norma EN 14488-7 [16], para determinar la dosificación real de fibras se utilizaron tres cilindros por cada dosificación. Los agregados fueron lavados inmediatamente después de elaborar los cilindros, con el fin de impedir que actuara la pasta cementante. Luego, las fibras fueron secadas y extraídas con un imán para calcular el peso. La dosificación real de fibras se calculó a partir del volumen del cilindro y el peso de las fibras. En la Tabla 4 se muestran los valores medidos de dosificación. Además, se realizaron ensayos para medir la masa unitaria en estado fresco, M, y el contenido de aire, A, del CRFA, conforme con los lineamientos de la norma NTC-1926 [17].

2.4.2 Ensayos para evaluar el comportamiento a compresión

Los ensayos de resistencia a compresión, de módulo de elasticidad y relación de Poisson del CRFA, se realizaron siguiendo los lineamientos de las normas NTC-673 [18] y NTC-4025 [19], respectivamente. Los ensayos se llevaron a cabo en una máquina universal marca Controls de referencia MC-66, con capacidad máxima de 2000kN. Para garantizar que la carga se distribuyera uniformemente en el cilindro, se utilizaron láminas de neopreno, tal como se especifica en la norma NTC-3708 [20].

En la Figura 2 se muestran las configuraciones de los ensayos. En el ensayo de módulo de elasticidad y relación de Poisson, al espécimen se le acopla el equipo de medición de deformaciones longitudinales y transversales, denominado compresómetro (Figura 2b). Para medir el desplazamiento en las direcciones longitudinal y transversal, se utilizaron transductores de desplazamiento tipo LVDT de referencia 82P0331/D, marca Controls, con capacidad máxima de 10 mm. Los ensayos se realizaron en el Laboratorio de Concretos del Programa de Ingeniería Civil de la Universidad Militar Nueva Granada.

En este estudio, el módulo de elasticidad del concreto representa el valor de la pendiente de la línea que une los puntos de la curva esfuerzo-deformación longitudinal correspondientes a una deformación de 0.00005 y al 40% de la carga máxima obtenida en los ensayos de resistencia a compresión (Ver Figura 1). La relación de Poissonse calculó de forma similar, pero utilizando el registro de deformaciones transversales.

3. RESULTADOS Y DISCUSIÓN

Para evaluar estadísticamente los resultados medidos y los obtenidos con las ecuaciones propuestas, en este estudio se utilizaron los siguientes parámetros: Promedio (X ), desviación estándar (S ), coeficiente de variación (CV ) y coeficiente de correlación (r ) .En el caso de ecuaciones de regresión con tendencias constantes, la precisión de la ecuación se evaluó a partir del CV. El coeficiente r mide la intensidad de la relación lineal entre los valores predichos por una ecuación y los datos obtenidos experimentalmente.

3.1 Propiedades en estado fresco

Los valores medidos (reales) de dosificación de fibras se muestran en la Tabla 3. Estas dosificaciones fueron claves para llevar a cabo un análisis adecuado de la información experimental de los especímenes. A partir de esta sección del artículo, los valores indicados de dosificación corresponden a los valores medidos.

Los valores medidos de asentamiento, contenido de aire, masa unitaria y peso específico (estado endurecido) se indican en la Figura 3. Se observa que el asentamiento disminuyó significativamente a medida que se aumentó el contenido de fibras, debido a que las fibras tratan de mantener unidos los componentes del concreto. Del mismo modo, el contenido de aire aumentó al adicionar las fibras de acero; el aumento fue aproximadamente del 65% (1.1%/1.7%) al incrementar la dosificación de cero (CS) a 11.6 kg/m³. Este aumento se originó por el incremento de vacíos de aire durante el mezclado de las fibras [21, 22, 23]. En cuanto a la masa unitaria y el peso específico, no se registraron cambios significativos de sus valores a medida que aumentó el contenido de fibras.

3.2 Comportamiento en compresión

En la Figura 3d se muestra la evolución de la resistencia del CS. En los primeros 7 días, la resistencia aumentó significativamente. Para los siguientes días se presentó ligero aumento hasta alcanzar una resistencia de 28.6 MPa a edad de 32 días. Este valor es 14.4% mayor que el valor de resistencia nominal del concreto (25 MPa). A edad de 335 días, el CRFA alcanzó una resistencia a compresión de 34.7 MPa. Este valor es 21.3% mayor que la resistencia nominal. En la Tabla 4 se presentan, para cada dosificación, las propiedades mecánicas promedio del CRFA sometido a esfuerzos de compresión.

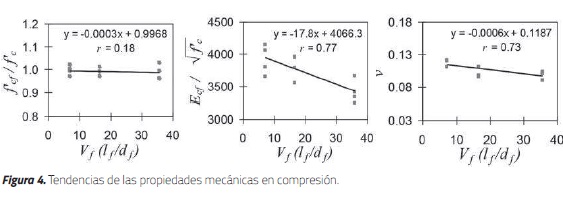
Con base en las propiedades medidas, en la Figura 4 se muestra la relación entre el producto V_f (l_f /d_f ) y las propiedades mecánicas en compresión. A partir de las tendencias de los datos medidos, se realizaron análisis de regresión lineal para estimar el efecto de la dosificación y el tipo de fibras de acero en el comportamiento del CRFA, sometido a esfuerzos de compresión.

En la Figura 4a se observa que la resistencia a compresión disminuyó levemente a medida que aumentó el producto V_f (l_f /d_f). De modo similar a lo reportado en otros estudios [21], esta tendencia se genera por la sustitución del agregado grueso por fibras de acero en la mezcla y por el aumento del contenido de aire (ver Figura 3a). En la Figura 4a se observa una línea con pendiente poco pronunciada y, por tanto, el coeficiente de correlación es bajo (r 0.18). En las Figuras 4b y 4c se observa que a medida que se incrementa el producto V_f (l_f /d_f ), el módulo de elasticidad y la relación de Poisson disminuyen. La disminución del módulo de elasticidad se origina por la sustitución del agregado grueso por fibras de acero. La disminución de la relación de Poisson se debe al confinamiento que las fibras generan en la matriz [21]. Los valores del coeficiente de correlación para las tendencias del módulo de elasticidad y la relación de Poisson son altos (r = 0.77 y r = 0.73, respectivamente), lo que indica una correlación adecuada de la ecuación con los datos medidos.

A partir del análisis de regresión lineal, en la Tabla 5 se presentan las ecuaciones propuestas para predecir el comportamiento del CRFA, sometido a esfuerzos de compresión. Las ecuaciones se proponen en función de la relación entre el producto Vf(lf/df) y las propiedades mecánicas en compresión, tales como fcf, Ecf y v. Aunque en la Tabla 5 se propone una ecuación para estimar fcf, para propósitos prácticos se puede considerar que fcf = fc (Figura 4a).

3.3 Comparación con modelos de predicción disponibles

Para cada modelo de predicción de f_cf y E_cf disponible en la literatura y para las ecuaciones propuestas en este estudio, se analizó estadísticamente el cociente entre los valores Predichos y Observados (P/O) de cada espécimen. Para los resultados del cociente P/O, se calculó el promedio (X ), la desviación estándar (S ), el porcentaje de sobre-predicciones (Sp ) y los valores extremos (Máx. y Mín.). El valor de Sp representa el cociente porcentual entre el número de datos en los que el valor del cociente P/O es mayor que 1.05 y el número de datos de la muestra analizada. Para facilitar la interpretación, los resultados estadísticos se muestran en la Figura 5 por medio de un diagrama de cajas y bigotes (Box and whisker chart, en inglés). En la Figura 5 se muestra el promedio (Círculo), la variación en términos de la desviación estándar (La altura total de la caja representa dos veces la desviación estándar) y los valores extremos (Línea continua). Un cociente entre la resistencia predicha y observada (Medida) menor que uno, indica que la predicción es conservadora; si es mayor que uno, la predicción es insegura.

3.3.1 Discusión de la predicción de f_cf

En la Figura 5a se observa que en los modelos de la literatura aquí estudiados, el valor de P/O es siempre mayor que uno, lo cual podría resultar inseguro. Por ejemplo, en los modelos de Prashant et al. y Mansur, el valor promedio de P/O es 1.03 y 1.06, respectivamente, y en los modelos de Elzeldin y Balaguru, Araujo, Nataraja et al. y Oliveira et al., el valor promedio es 1.05. En estos últimos cuatro modelos, la variación de los datos es relativamente baja (3.56%, 3.55%, 3.51% y 3.51%, respectivamente) y sus valores extremos están cerca de la caja; sin embargo, la sobre-predicción es alta (41.7%).

Se considera que el modelo propuesto en este estudio para estimar la resistencia a compresión del CRFA es adecuado, ya que el valor de P/O es 1.00, la variación de los datos es baja (2.23%), los valores extremos están muy cercanos al promedio, y la sobre-predicción es baja (8.33%). Adicionalmente, la versatilidad del modelo es adecuada, ya que éste incluye las variables V_f (l_f /d_f ) y f_cf.

3.3.2 Discusión de la predicción de Ecf

En la Figura 5b se observa que en los dos modelos de Prashant et al., el valor de P/O es cercano y ligeramente inferior a uno (0.94 y 0.95, respectivamente), lo que indica que los modelos proporcionan, en promedio, una predicción acertada de E_cf, a pesar que corresponden a E_cf secante al 45%. Sin embargo, la variación y la sobre-predicción de estos dos modelos es relativamente alta (16.7% y 25.7%, respectivamente). Adicionalmente, la forma funcional del segundo modelo (Prashant et al.2) no es adecuada para fines prácticos de diseño, ya que la ecuación tiene forma exponencial.

En el modelo de Mármol, el valor de P/O es mayor que uno (1.21), y la variación y la sobre-predicción es alta (75.0%). En cuanto al modelo de Ponce, el valor de P/O es significativamente mayor que uno (2.17), lo que indica una sobre-predicción del 100%, y por tanto, los resultados no se indican en la figura.

Se considera que el modelo propuesto en estudio para estimar el módulo de elasticidad de CRFA es adecuado, ya que el valor de P/O es muy cercano y menor que uno (0.99), la variación de los datos es relativamente baja (5.69%), los valores extremos están muy cercanos al promedio y la sobre-predicción es baja (16.7%). Adicionalmente, el modelo incluye variables fácilmente identificables por parte del diseñador, tales como V_f (l_f /d_f ) y f_cf.

3.4 Discusión de la predicción de la curva esfuerzo-deformación

En la Figura 6 se muestran las curvas esfuerzo-deformación del CRFA sometido a esfuerzos de compresión, predichas con los modelos que se discutieron en la sección 1.1. Los modelos estudiados son de fácil aplicación, ya que únicamente dependen de V_f y f_c.

En las gráficas de la Figura 6 se observa que en los modelos de la literatura aquí estudiados, la dispersión de los resultados de deformación es significativamente alta. Por tanto, en estudios experimentales futuros se debe incluir la medición de la curva completa esfuerzo-deformación del CRFA sometido a esfuerzos de compresión, para proponer una ecuación que se ajuste a las tendencias de los materiales locales de construcción.

3.5 Limitaciones

Para utilizar las ecuaciones propuestas en este estudio, el CRFA debe cumplir con las siguientes características: (i) Concreto de peso normal (Masa unitaria entre 2250 kg/m³ y 2350 kg/m³), con resistencia a compresión – entre 25 MPa y 35 MPa, y (ii) Fibras de acero con gancho, dosificación de fibras de 15 a 60 kg/m³ y, valor del producto V_f (l_f /d_f ) entre 7.1 y 36.1%.

4. CONCLUSIONES

En el artículo se han presentado los resultados de un estudio analítico y experimental para evaluar el comportamiento del concreto reforzado con fibras de acero ZP- 306, sometido a esfuerzos de compresión. En el estudio se ha evaluado la resistencia a compresión, el módulo de elasticidad y la relación de Poisson. La investigación incluyó la discusión de cinco modelos para predecir la curva esfuerzo-deformación del CRFA, de seis modelos para predecir la resistencia a compresión y de cuatro modelos para predecir el módulo de elasticidad. El programa experimental comprendió el ensayo de 48 muestras en forma de cilindros. A partir de las tendencias de los resultados experimentales, se propusieron correlaciones numéricas para estimar las principales propiedades mecánicas del CRFA. Las conclusiones de la investigación se presentan a continuación:

- El valor de la masa unitaria del CRFA permaneció casi constante a medida que incrementó el volumen de fibras en la mezcla. Sin embargo, el contenido de aire aumentó con el incremento del volumen de fibras agregado a la mezcla. Este aire es introducido al momento del mezclado de las fibras con el concreto.

- A medida que incrementó el producto V_f (l_f /d_f ), la resistencia a compresión disminuyó levemente. Esta tendencia se genera por la sustitución de agregado grueso por fibras de acero en la mezcla y por el aumento de contenido de aire incluido en el momento del mezclado. Sin embargo, para propósitos prácticos se puede suponer que la resistencia a compresión del CRFA es igual que la resistencia del CS.

- Las fibras de acero le generan un efecto de confinamiento al concreto, ya que al incrementar el contenido de fibras, disminuyó la relación de Poisson.

- Se considera que los modelos de predicción disponibles en la literatura para estimar f_cf son de aplicación sencilla, ya que las ecuaciones incluyen ecuaciones fácilmente identificables por el diseñador.

- Las ecuaciones de los modelos disponibles en la literatura para predecir la curva esfuerzo-deformación tienen un formato práctico y variables que incluyen el efecto de las fibras en la forma de la curva. Sin embargo, la dispersión de los resultados de la deformación es significativamente alta. Por tanto, en estudios experimentales futuros se debe incluir la medición de la curva completa esfuerzo-deformación del CRFA sometido a esfuerzos de compresión, para así plantear una ecuación que se ajuste a las tendencias de los materiales de construcción del país.

- La ecuaciones aquí propuestas para estimar la resistencia a compresión, el módulo de elasticidad y la relación de Poisson dependen de parámetros básicos de diseño, tales como f_cf y V_f (l_f /d_f ) y, por tanto, se considera que el formato de las ecuaciones es práctico y versátil para ser incluidas en un reglamento de diseño. Además, la predicción de las ecuaciones propuestas son acertadas, y la variación y sobre- predicción de los datos son bajas.

AGRADECIMIENTOS

Los autores agradecen a las empresas Argos y Proalco por donar el concreto y las fibras, en especial a los ingenieros Diego Velandia y Liliana Cardona, respectivamente. Adicionalmente, agradecen al Ing. Miguel Ospina, a la Ing. Pahola Porras y al Técnico Oliverio Pinzón, por colaborar en la realización de los ensayos en el Laboratorio de Concreto del Programa de Ingeniería Civil de la Universidad Militar Nueva Granada.

REFERENCIAS

[1] Malatesta S. y Contreras M. (2009). Comportamiento al corte de hormigones reforzado con fibras de acero. Tesis, Universidad Técnica Federico Santa María, Valparaíso - Chile.         [ Links ]

[2] Baczkowski B. y Submitted T. (2007). Steel fiber reinforced concrete coupling beams. Ph.D. thesis, University of Science and Technology, Hong Kong.         [ Links ]

[3] Nataraja M., Dhang N. y Gupta A. (1999). Stress-strain curve for steel fiber reinforced concrete in compression. En: Cement and concrete composites, Vol. 21, pp. 383- 390.         [ Links ]

[4] Popovics S.(1973). A numerical approach to the complete stress-strain curve of concrete. En: Cement and concrete research, Vol. 3, No. 5, pp. 583-599.         [ Links ]

[5] Carreira D. y Chu K. (1985). Stress-strain relationship for plain concrete in compression. En: ACI Journal, Vol. 82, No. 6, pp. 797-804.         [ Links ]

[6] Ezeldin A., Balaguru, P. (1992). Normal and high-strength fiber-reinforced concrete under compression. En: Journal of materials in civil engineering, Vol. 4, No. 4, pp. 415-429.         [ Links ]

[7] Mansur M., Chin M.S. y Wee T. (1999). Stress-strain relationship of high-strength fiber concrete in compression. En: Journal of materials in civil engineering, Vol. 11, No. 1, pp.21-29.         [ Links ]

[8] Araújo D. (2002.). Cisalhamento entre viga e laje pré-moldadas ligadas mediante nichos preenchidos com concreto de alto desempenho.Tese de D.Sc., Universidade de São Paulo, Escola de Engenharia de São Paulo, Brasil.         [ Links ]

[9]. Nataraja M.C., Dhang N. y Gupta A.P. (1998). Steel fiber reinforced concrete under compression. En: The Indian Concrete Journal, Vol. 26, pp.353-356.         [ Links ]

[10] Oliveira L., Dos Santos V., Ribeiro A., Ramos D., Araujo D., Khalil M. y Rodriguez P. (2010). Stress-strain curve for steel fiber reinforced concrete in compression; Río de Janeiro. En: Matéria, Vol.15, No. 2, pp. 260-266.         [ Links ]

[11] Prashant Y., Nagarnaik P., Pande A. (2011). Performance of steel fiber on standard strength concrete in compression. En: International journal of civil and structural engineering, Vol. 2, No 2, pp. 483-492.         [ Links ]

[12] Prashant Y., Nagarnaik P., Pande A. (2011). Effect of steel fibers on modulus of elasticity of concrete. En: International journal of civil and structural engineering, Vol. 7, No. 2, pp.169-177.         [ Links ]

[13] Ponce D. (2008). Hormigones de altas presentaciones. Proyecto fin de carrera, Universidad Politécnica de Cartagena, Colombia.         [ Links ]

[14] Mármol P. (2010). Hormigones con fibras de acero, características mecánicas.Tesis de Maestría, Universidad Politécnica de Madrid, España.         [ Links ]

[15] ICONTEC. Norma Técnica Colombiana NTC 396. Método de ensayo para determinar del asentamiento del concreto. Bogotá D.C.,1992, pp. 6.         [ Links ]

[16] AENOR. Norma Técnica Española EN 14488-7 Ensayos de hormigón proyectado Parte 7 - Contenido en fibras del hormigos reforzado con fibras. Madrid España, 2007, pp. 10.         [ Links ]

[17] ICONTEC. Norma Técnica Colombiana NTC 1926 Método de Ensayo para Determinar la Masa Unitaria del Concreto. Bogotá D.C., 1995, pp. 7.         [ Links ]

[18] ICONTEC. Norma Técnica Colombiana NTC 673 Ensayo de resistencia a la compresión de cilindros normales de concreto. Bogotá D.C., 2000, pp.14.         [ Links ]

[19] ICONTEC. Norma Técnica Colombiana NTC 4025 Método de ensayo para determinar el módulo de elasticidad estático y la relación de Poisson en concreto a compresión. Bogotá D.C., 2006, pp.11.         [ Links ]

[20] ICONTEC. Norma Técnica Colombiana NTC 3708. Uso de refrentado no adherido para la determinación de la resistencia a la compresión de cilindros de concreto endurecido. Bogotá D.C., 1995, pp.10.         [ Links ]

[21] Carrillo J., González G., y Aperador W. (2013). Correlaciones entre las propiedades mecánicas del concreto reforzado con fibras de acero. En: Revista Ingeniería, Investigación y Tecnología, Vol. 14, No. 3, pp.435-450.         [ Links ]

[22] Kalman D. (2010). Use of steel fiber reinforced concrete for blast resistant design. Tesis de Maestría. Kansas State University. Manhattan, Kansas, EUA.         [ Links ]

[23] Miao B, Cher J. y Yang Ch. (2003). Influences of fiber content on properties of self-compacting steel fiber reinforced concrete. En: Journal of the Chinese Institute of Engineers, Vol. 26, No. 4, pp.523-537.         [ Links ]