Introducción
Los sistemas tipo push (empujar) hacen referencia a la manera en que se envían los trabajos al sistema de producción y cómo es su flujo a través [1]. En este tipo de sistema, se determina una fecha de entrega para cada trabajo de acuerdo con el tiempo que toma al material pasar por el sistema de producción sin importar lo que suceda delante de él, es decir, los trabajos son empujados por el sistema. Por otra parte, un sistema de producción tipo pull (halar) permite principalmente que una empresa realice los productos para ser entregados en el momento preciso y en la cantidad requerida por los clientes, y utilice para ello las cantidades necesarias de su inventario, para así evitar su desperdicio y los costos que estos conllevan [2].
Las empresas en el mundo han venido transitando en los últimos años de los sistemas tipo push a combinaciones push/pull y, finalmente, a sistemas tipo pull [3]. En la industria local y regional, son pocas las empresas que emplean realmente sistemas tipo pull, lo que se evidencia en un trabajo de investigación reciente en que se realizó un estudio con 13 empresas importantes en Manizales y se resalta en ellas el predominio del sistema tipo push, aunque se encontraron sistemas híbridos de programación de la producción [4].
La simulación se ha convertido, hoy día, en una herramienta muy valiosa para analizar los procesos productivos, ya que permite describir el comportamiento de determinado sistema, comparar diferentes configuraciones de dicho sistema sin incurrir en mayores costos y proponer alternativas para mejorar los procesos productivos y reducir los costos de producción [5-6]. La simulación busca definir un modelo, construirlo, verificarlo, experimentar con él, analizar resultados y validarlo [7].
Así es que se encuentran estudios sobre el uso de la simulación en sistemas tipo push y combinaciones push/pull en diversas industrias y en diferentes condiciones operativas [8], por ejemplo, en el comportamiento de los niveles de inventario en un sistema de producción controlado Kanban [9], en un sistema just-in-time [ 10], en la comparación del rendimiento de los sistemas tipo push con el de los sistemas tipo pull bajo diferentes condiciones de operación [11], en niveles mínimos de rendimiento para dos tarjetas de líneas de control Kanban [12], en una línea de ensamble electrónico [13], en un sistema automatizado tipo híbrido push/pull para manejo de materiales [14], entre otros. Asimismo, se encuentran otros trabajos de simulación, como el desarrollo de un algoritmo genético basado en información obtenida en la simulación de un caso hipotético de un sistema de manufactura tipo pull [15] y el modelo de simulación de un sistema tipo pull con variables de entradas como la cantidad de Kanban en cada puesto, y variables de desempeño, como el porcentaje de demanda satisfecha [16].
Algunos trabajos recientes muestran el uso del software ProModelTM para la simulación como el estudio comparativo entre sistemas de control de la producción tipo pull basados en tarjetas Kan-ban [17], la simulación de eventos discretos como apoyo a la modelación de operaciones logísticas involucradas en la exportación marítima de commodities en las presentaciones de carga suelta y granel desde 12 empresas productoras hasta el puerto marítimo [18] y en el diseño de una simulación del proceso de una celda de manufactura flexible (FMC, por sus siglas en inglés) para medir y elegir la alternativa de solución que mejore en mayor grado la productividad del sistema actual [19].
A pesar del uso extendido de la simulación en el mundo, en la industria regional y local no se hace uso masivo de tal herramienta, tal vez por desconocimiento de las potencialidades que esta tiene o por la falta de acceso de las empresas a esta tecnología.
En este trabajo, se presenta el resultado de una propuesta de simulación de uno de los procesos productivos de una empresa local. Se logró simular su propio sistema de producción, que resultó ser una combinación push-pull, y se planteó un nuevo sistema de producción pull como una alternativa para reducir los costos de producción en una de sus líneas. La propuesta se basa en herramientas cuantitativas que permiten analizar la conveniencia de realizar proceso de subcontratación, para lo que se ha desarrollado una fórmula basada en los pedidos y los estándares para fabricar partes que permite visualizar qué conjuntos de piezas será más conveniente subcontratar, en busca de conocer los beneficios de adoptar un sistema tipo pull.
Marco teórico
Sistemas tipo push
Los sistemas push, o empujar, están constituidos tanto por conceptos administrativos como por un componente técnico que hace referencia a la forma en que los trabajos se mueven por el sistema de producción. En estos sistemas, los trabajos inician en una fecha determinada y se fija una fecha para su entrega de acuerdo con los requerimientos de mercadeo. Los tiempos para la entrega de los productos son un parámetro de planeación determinístico, mientras los tiempos reales que le toma al material pasar por el sistema de producción es variable. El material se mueve a través del sistema de producción pasando de un proceso a otro y no importa lo que suceda delante de él, por eso el nombre de "empujar", ya que el material es empujado por el sistema de producción. Otro nombre para los sistemas push es sistemas basados en el programa, puesto que el programa empuja la producción. A los sistemas push subyace un concepto administrativo de planeación central, en el que las decisiones sobre cómo debe procesarse las órdenes de producción son centralizadas. Estas decisiones se empujan después a niveles más bajos de la organización y deben cumplir con el programa central generado [20].
Dentro de los sistemas push, se encuentran los sistemas de planeación de requerimientos materiales (MRP), que son métodos para la planeación efectiva de todos los recursos de una organización de manufactura. Estos sistemas se emplearon inicialmente para planear de nuevo al actualizar las fechas de entrega de las órdenes en la planta, lo que dio como resultado un desempeño mejorado de las ventas y de la planta misma. Siguieron algunos intentos para mejorar la planeación de producción, resultado de ello es el programa maestro de producción (MPS) y los pronósticos de demanda. Con un mejor MPS incorporado al MRP, este se convirtió en un sistema MRP de ciclo cerrado.
La siguiente etapa fue mejorar la planeación de la capacidad en distintos niveles y agregar habilidades de simulación [2].
Sistemas tipo pull
Un sistema de producción tipo pull, o halar, permite, principalmente, que una empresa realice los productos para ser entregados en el momento preciso y en la cantidad requerida por los clientes [21]. Estos sistemas tienen como característica principal generar productos de máxima calidad a través de una producción que utilice las cantidades necesarias de su inventario, de materias primas, de producto en proceso o de producto terminado, con el fin de evitar su desperdicio y los altos costos en relación con las cantidades y los precios de los materiales necesarios para cada producto [22]. Los sistemas pull tienen como característica su enfoque para manejar la interdependencia, en particular en las operaciones de manufactura [23]. El ciclo de un sistema tipo pull permite conocer claramente cuál es su objetivo principal: lograr que sea la demanda la que atraiga a la producción y no la producción la que sea empujada al cliente [22].
Dentro de los sistemas tipo pull, se encuentran los just-in-time (JIT) y la teoría de las restricciones (TOC, por su siglas en inglés). Los sistemas JIT se pueden traducir como justo a tiempo. Estos ya no son un sistema de producción para fabricar el tipo de unidades necesarias, en el tiempo necesario y en las cantidades necesarias [24], sino que son más bien un concepto que debe adoptarse. JIT se refiere a todo el sistema, al control de flujo de materiales y a una filosofía administrativa. Se requieren cuatro métodos básicos para el éxito de un sistema JIT: limitación de desperdicio, participación de los empleados en la toma de decisiones, participación de los proveedores y control total de la calidad. Por otra parte, están los sistemas TOC, cuya premisa básica es que la salida del sistema está determinada por sus restricciones. La definición de restricción sugiere que TOC tiene una aplicación más amplia que la planeación y el control de la producción.
Materiales y métodos
La metodología usada en este trabajo consistió en tres etapas: la primera fue el reconocimiento del proceso de producción de la empresa, la segunda fue la determinación de los ciclos en los procesos y los tiempos tanto de llegada de la materia prima como de procesamiento de cada parte y la tercera fue la construcción del modelo de simulación tanto del sistema actual como de la propuesta para mejorarlo. A continuación, se describen estas etapas.
Reconocimientos de los procesos de manufactura de la empresa y determinación de los tiempos de llegada
En esta etapa, se realizó el reconocimiento de los diferentes procesos de manufactura de la empresa, de los elementos que esta construye y distribuye, y de las partes que componen cada elemento. Se realizaron los diagramas de flujo de producción de cada producto que la empresa vende, al que llamaremos elemento, de cada parte y de sus diferentes subpartes, lo que permitió una familiarización con el proceso y un reconocimiento de los datos más relevantes que deberían incluirse en el modelo para simularlo.
La empresa fabrica, entre otros, partes de un producto denominado elemento 1 que se entregan al cliente quien debe ensamblar el producto. Para fabricar un elemento 1, se necesitan tres partes que se producen de manera independiente: la parte X, la parte Y y la parte Z. A su vez, cada parte está formada por subpartes, por ejemplo, para la parte X, son necesarias 6 subpartes (X1, X2,..., X6), para la parte Y cuatro subpartes (Y1,..., Y4) y para la parte Z tres subpartes (Z1,.., Z3). En la figura 1, se muestra el diagrama de flujo del proceso para el elemento 1, que es en paralelo.
En el conocimiento del proceso, se determinó que la empresa fabrica todas las subpartes necesarias para ensamblar el elemento 1. Así, por ejemplo, de las distintas piezas de materia prima empleadas se obtiene un número determinado de subpartes. Estos números para cada subparte de la parte X se presentan en la tabla 1.
Tabla 1 Estándares y tiempos de procesamiento usados en la fabricación de la parte X del elemento 1
| Parte X | |||
|---|---|---|---|
| Subparte | Estándar | Tiempos de procesamiento en minutos | Tamaño de muestra para la prueba de bondad de ajuste |
| X1 | 19 | N(121;3,5) | 100 |
| X2 | 15 | N(175;5) | 100 |
| X3 | 24 | N(121;3,2) | 150 |
| X4 | 13 | N(1573;2,2) | 120 |
| X5 | 12 | N(1087;0,9) | 200 |
| X6 | 32 | N(10;2,1) | 100 |
Fuente: Elaboración propia.
A continuación, se midieron los tiempos de llegada entendidos como los tiempos entre las distintas unidades de cada materia prima necesarias para producir cada subparte. Estos tiempos son variables y dependen de los pedidos y de la disponibilidad de material, por tanto, se consideran como una variable independiente para el modelo.
Después se realizaron las medidas de los tiempos necesarios para la producción de las distintas subpartes en cada estación de trabajo, que se denominarán tiempos de procesamiento. Estos tiempos se tomaron varias veces, y se realizaron análisis de las distribuciones con el fin de obtener las medias y desviaciones de tales medidas, que siguieron una distribución normal. Estos tiempos de procesamiento son insumos indispensables para la simulación de los procesos. En la tabla 1, se presentan los tiempos determinados para la fabricación de cada subparte que conforma la parte X, los que se expresan en términos de la media y de la desviación estándar.
Construcción del modelo de simulación
Se usó el software de simulación Promodel versión estudiantil (ProModel Student versión: 7.0.4.201) para construir un modelo tipo pull basado en sub-contratación de partes que mejorará la versión actual de la fabricación del elemento 1. En el proceso actual, se construyen tantas cantidades de las subpartes X1,…,X6 como partes X se pidan, lo que está bien dentro de un modelo tipo pull; el detalle es que para construir una sola unidad de subparte Xi, por razones de dimensiones de la materia prima, se requiere comprar material del que salen varias subpartes Xi, es decir, no es posible comprar materiales para construir una cantidad exacta de Xi, sino que es necesario incurrir en inventarios. Para el planteamiento del modelo, se emplearon dos criterios: los estándares y las penalizaciones, que se describirán a continuación.
Estándares
Para ensamblar un elemento 1, se necesita una parte X que se constituye, por ejemplo, de una sola subparte X1, pero la empresa tiene que incurrir en el costo resultante de comprar un material del que salen 19 subpartes X1. El valor 19 se denominará el estándar de la subparte X1. En general, cada subparte de X, así como las subpartes de Y y de Z, tienen estándares que indican cuántas subpartes se fabrican con el material principal.
El modelo de simulación realizado en Promodel se ha programado de tal forma que calcule el costo en que se incurre al comprar los materiales a fin de fabricar las subpartes que se necesitan para manufacturar las partes del elemento 1. Si el pedido es, por ejemplo, de un solo elemento 1 y el estándar para la subparte X1 es 19, quiere decir que 18 subpartes X1 tendrán que ser guardadas en el almacén de producto en proceso y solo 1 subparte X_1 se usará para satisfacer el pedido; por tanto, aunque se fabrique un solo elemento 1, el costo del material de la subparte X1 se calcula con el estándar; tal costo tiene incluido el costo de mano de obra y del material, el y costo de almacenamiento.
Penalización
Con el fin de comparar el modelo actual de manufactura de la empresa tipo combinación pull/push con el propuesto tipo pull, se propone una medida que se denominará penalización denotada por P. La penalización P se ha definido mediante la ecuación (1), en la que el cociente entre el pedido y el estándar ETi da cuenta de la utilización del material. El subíndice i se refiere a la subparte i, mientras que ETi es el estándar de la subparte i. La penalización será grande si hay muchos desajustes entre el pedido y los estándares.
Nótese que, si el pedido es muy pequeño comparado con el estándar i, el factor (1-(Pedido)/ (ETi)) será cercano a 1 y la contribución de la subparte a la penalización será grande en la sumatoria de las penalizaciones.
La ecuación (1) causará penalizaciones grandes si la empresa tiene que entregar bajos pedidos y requiere procesar para guardar muchas piezas en inventario para fabricar las distintas partes, debido a que los estándares son más grandes que el pedido.
En caso de que el pedido supere el estándar, debe cambiarse por la cantidad que afecta la penalización. Por ejemplo, si el estándar de una subparte es 19 y el pedido de esta subparte es 20, entonces sería necesario comprar 2 materiales de los que saldrían 38 subpartes y se usarían 20 y, por tanto, será necesario almacenar 18; en este caso, la pena-lización es sobre el material que sobró y se calcularía con el sumando (1-(Pedido)/(ETi)) = (1-(1/19)), que es un valor mayor de 0. De esta forma, en la ecuación (1), no hay forma de que haya un ésimo sumando que tome un valor negativo.
Se ha simulado un sistema basado en subcontrataciones en que la empresa pide a terceros todas las piezas que necesita y no incurre en penaliza-ciones. Sin embargo, puede ser que solo sea posible subcontratar cierto porcentaje de las subpartes necesarias para fabricar un elemento 1 y, por tanto, habrá unas penalizaciones, por lo que la medida creada en la ecuación (1) mostrará qué tanto son las penalizaciones en ese caso y podrán ser comparadas con el sistema actual de la empresa.
Resultados y discusión
En esta sección, se presentan los resultados obtenidos, que se dividen en dos aspectos: primero, se describe una metodología generalizada que se ha seguido para el presente caso de estudio y se ha descrito en la sección materiales y métodos para el caso de estudio en particular. A continuación, se presentan los resultados relacionados con el análisis de la penalización propuesta y las comparaciones de las distintas versiones de fabricación para este caso de estudio.
Definición de una metodología generalizada
Según los resultados de la experiencia práctica, el uso de la simulación y la creación de una medida de penalización se definió una metodología generalizada que puede ser aplicable en distintos casos de procesos manufactureros. La metodología consiste en los siguientes pasos:
■ Paso 1: Haga un estudio de los procesos y construya diagramas de procesos.
■ Paso 2: Tome tiempos aleatorios de operación y realice pruebas de bondad de ajuste.
■ Paso 3: Realice una simulación del proceso actual e introduzca la variable tiempo de ciclo como indicador de este proceso.
■ Paso 4: Realice simulaciones de alternativas de solución e introduzca la variable tiempo de ciclo como indicador de este proceso.
■ Paso 5: Obtenga varias réplicas de los modelos es-tocásticos de simulación y una muestra aleatoria de cada uno.
■ Paso 6: Realice un análisis de varianza para detectar diferencias significativas entre el modelo actual y las alternativas.
■ Paso 7: En los anteriores modelos de simulación, programe la fórmula de penalización y alimente estos modelos con los pedidos reales.
Se recomienda tomar la decisión de cuál alternativa es mejor usando los criterios tiempo de ciclo y penalización generada. Esta metodología ayudará a tomar decisiones y a fortalecer los procesos productivos mediante herramientas científicas. A continuación, se presentan los resultados para el caso de estudio considerando la penalización y los distintos modelos de producción.
Análisis de la penalización
Considerando que la fabricación del elemento 1 necesita una parte X y que a su vez dicha parte necesita la fabricación de subpartes, se aplicó la ecuación (1) para las siguientes dos situaciones: la primera, para una versión actual de fabricación de la parte X tipo push, y la segunda, para la fabricación de la misma parte en dos posibles versiones tipo pull que consideran subcontrataciones. El análisis se ha realizado para un pedido de 5 elementos 1. Se pueden observar en la tabla 2 los estándares actuales que la empresa usa para producir subpartes de la parte X. Para aclarar esta idea, obsérvese que para producir una sola parte X hay que comprar un material principal del que salen 19 subpartes X1 y otro material del que producen 15 subpartes X2, y así sucesivamente. Las compras mencionadas parten del supuesto de que no hay inventarios de las subpartes X1 y X2. Se ha considerado, en la versión 1 pull, la situación en que sea posible subcontratar la fabricación de las subpartes X1, X2 y X4; por ello, en la tabla 2, los estándares correspondientes son 5, lo que quiere decir que para un pedido de 5 elementos 1 que necesitan de 5 partes X se tendría que subcontratar la fabricación de 5 subpartes X1, 5 de X2 y 5 de X4. Como se está subcontratando, la contribución de estos materiales a la penalización es 0, por lo que el estándar tiene que ser 5, ya que se adapta al pedido de 5 elementos 1. Nótese que se tuvo una penalización de la versión pull 1 de 2,0425, menor que la versión push actual. En la versión pull 2, se ha considerado la alternativa de subcontratar la fabricación de las subpartes X3, X5 y X6 tras lo cual se obtuvo una penalización de 2,1952. La primera versión ocasiona menos penalización que otras consideradas.
Tabla 2 Cálculo de la penalización de la versión push y dos versiones pull en la fabricación de la parte X
P = 4,2376 P = 2,0425 P = 2,1952
Fuente: Elaboración propia.
El análisis de penalización que se ha realizado, y se muestra en la tabla 2, es una muestra de alternativas que se pueden analizar; sin embargo, hay múltiples formar de subcontratar, desde todas las subpartes, todas menos una, todas menos dos, y así hasta la situación de fabricarlas todas. Estas múltiples alternativas tendrán cada una alguna penalización, así que el método de penalización propuesto en este caso permite tomar decisiones acerca de qué es más conveniente subcontratar, sujeto a que sea posible hacerlo, y en qué subpartes sea más conveniente.
Comparación de versiones de fabricación
Se han considerado tres versiones de fabricación: una versión actual tipo push y dos versiones proyectadas tipo pull. En las últimas dos versiones, se ha considerado la subcontratación de un conjunto de partes, tal como se evidencia en la tabla 2, y que fue explicado en la sección anterior. Como criterio de comparación de las tres versiones, se introdujo la variable aleatoria a la que se denominó tiempo de ciclo, que permite calcular los tiempos empleados en cada versión para llevar a cabo el proceso. Esta variable se calcula considerando los tiempos de llegada y los tiempos de procesamiento medidos en el proceso de manufactura que se presentaron en la tabla 1. El cálculo de estos tiempos de ciclo es un resultado del modelo en Promodel. Se usaron 25 réplicas en un modelo estocástico que produce resultados aleatorios diferentes en cada réplica.
Se hizo una comparación de medias mediante un análisis de varianza ANOVA, por sus siglas en inglés; en la tabla 3, se muestra un análisis de varianza hecho en el software R. Los resultados sugieren que hay diferencias significativas entre los tiempos de ciclo.
Tabla 3 Análisis de varianza de las versiones consideradas
| Df | Sum Sq | Mean Sq | F value | Pr (>F) | |
|---|---|---|---|---|---|
| Grupo | 2 | 1816,3 | 908,1 | 531.2 | <2e-16 |
| Residuals | 72 | 123,1 | 17 | ||
| Signif. codes | 0 ‘***’ 0,001 ‘**’ 0,01 ‘*’ 0,05 ‘.’ 0,1 ‘ ’ 1 |
Fuente: Elaboración propia.
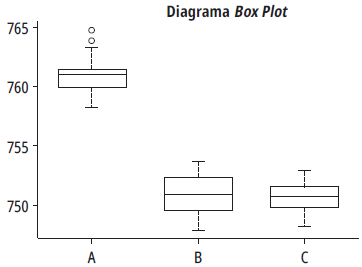
Ante el análisis mostrado en la tabla 3, es necesario verificar qué tratamiento, en este caso qué configuración, es diferente de otra. El tratamiento A corresponde a la configuración push versión actual, el tratamiento B a la configuración pull versión 1 y el tratamiento C a la configuración pull versión 2 (figura 2). En esta figura, se nota que las versiones pull, la 1 y la 2 (tratamientos B y C), son diferentes estadísticamente del tiempo de ciclo de la versión push actual.
Diferencias significativas de los tratamientos A, B y C
Como en la figura 2 se observan diferencias entre el tratamiento A comparado con los tratamientos B y C, se ha realizado un análisis pos-ANOVA que permita, de manera analítica, rectificar tales diferencias. Las tablas 4 y 5 muestran comparaciones Tukey y Fisher, respectivamente, pruebas que se consiguieron a través del software Minitab versión 18.
Tabla 4 Prueba Tukey con confianza del 95% para comparación de medias
| Grupo | N | Media | Agrupación | ||
|---|---|---|---|---|---|
| A | 25 | 761,093 | A | ||
| B | 25 | 750,955 | B | ||
| C | 25 | 750,541 | B | ||
Fuente: Elaboración propia.
Tabla 5 Prueba Fisher con el 95% de confianza para comparación de medias
| Grupo | N | Media | Agrupación | ||
|---|---|---|---|---|---|
| A | 25 | 761,093 | A | ||
| B | 25 | 750,955 | B | ||
| C | 25 | 750,541 | B | ||
Fuente: Elaboración propia.
Ambas comparaciones de las dos tablas muestran que los tratamientos B y C difieren estadísticamente del tratamiento A, lo que confirma que las versiones pull 1 y 2 presentan tiempos de ciclo muy diferentes de la versión actual tipo push.
Como se ha demostrado que las versiones Pull 1 o versión pull 2 (tratamientos B y C) son estadísticamente iguales, entonces la pregunta es ¿cuál de las dos versiones elegir? La respuesta puede estar en el análisis de penalización; aquella versión que ofrezca menos penalización podría ser la que se elija. Es importante aclarar que el análisis de penalización se puede complementar con otros análisis de costos y calidad para tomar las decisiones adecuadas.
Verificación de supuestos
Con el fin de darle soporte a la prueba ANOVA en el punto anterior, se realizó la verificación de supuestos, para tal efecto se presenta la figura 3. En la parte superior izquierda, se verifica que los residuales tienen media 0 y están homogéneamente distribuidos; en la parte superior derecha, se puede verificar la homogeneidad de las varianzas y que los residuales se mueven alrededor de 0; en la parte inferior izquierda, los residuales no muestran ningún patrón, lo que indica independencia de los errores, de modo que esto es positivo para el análisis; por último, en la parte inferior derecha, se detecta que los residuales siguen una distribución normal con media 0.
Análisis de regresión
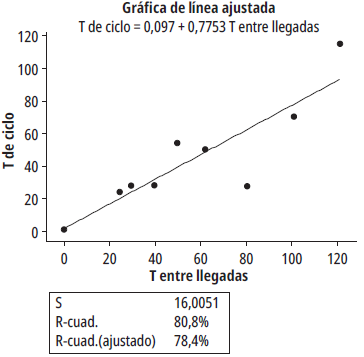
Se ha estudiado el ritmo de las entradas del material en el proceso de producción de la subparte X y se ha relacionado la variable tiempo de ciclo con la variable tiempo entre llegadas. En un modelo de simulación construido en Promodel, se han variado los tiempos de llegadas de todas las materias primas para producir la subparte X. Los ritmos o las tasas a las que llega el material sirven para verificar si los tiempos de ciclo mejoran o empeoran. La figura 3 muestra una gráfica de regresión construida en el software Inffostat, en que la variable regresora es el tiempo entre llegadas de las materias primas y la variable dependiente es el tiempo de ciclo. Se puede detectar en esta figura que, a medida que los tiempos entre llegadas se hacen mayores (ritmos lentos de llegada de materia prima), los tiempos de ciclo son mayores.
Nótese también en la figura 3 que, a medida que los tiempos entre llegadas se hacen pequeños (ritmos rápidos de llegada de materia prima), los tiempos de ciclo se hacen pequeños. Estos análisis de ritmos de llegada confirman que las llegadas de material a ritmos fuertes y elevados disminuyen los tiempos de ciclo; la razón principal es que los inventarios entorpecen el flujo de los materiales por el proceso. La recomendación entonces es mantener los ritmos de llegada lo más lentos posible; es mejor utilizar pedidos justo a tiempo, es decir, que, si se piden 5 elementos 1, se deben emplear las materias primas adecuadas para producir 5 elementos 1. Lo anterior indica que en lo posible es adecuado subcontratar la mayor cantidad de partes que se puedan desde que no vaya en detrimento de la calidad y de otros factores importantes que la empresa desee cuidar.
En la tabla 6, se muestra una salida de la regresión, construida en el software Minitab 18, para tener un análisis más analítico y no solo gráfico del modelo de regresión. El resultado sugiere que hay una relación directa entre tiempos de ciclo y tiempos entre llegadas, en que la constante no es significativa, pero sí lo es la pendiente. Los errores, según el ANOVA, son pequeños comparados con el modelo de regresión, así que el modelo explica la mayor variabilidad y no tanto los errores. También en la figura 4 se detecta un coeficiente de regresión de 0,8084, lo que indica una buena relación lineal entre las dos variables.
Tabla 6 Análisis de regresión tiempo de ciclo versus tiempo entre llegadas
| Resumen del modelo | |||||
|---|---|---|---|---|---|
| S | R-cuad. | R-cuad (ajustado) | R-cuad. (pred) | ||
| 16,0051 | 80,84 % | 78,45 % | 65,56 % | ||
| Coeficientes | |||||
| Término | Coef. | EE del coef. | Valor T | Valor p | FIV |
| Constante | 0,10 | 8,47 | 0,01 | 0,991 | |
| T entre llegadas | 0,775 | 0,133 | 5,81 | 0,000 | 1,00 |
| ANOVA | |||||
| Fuente | GL | SC ajust. | MC ajust. | Valor F | Valor p |
| Regresión | 1 | 8648 | 8648,2 | 33,76 | 0,000 |
| T entre llegadas | 1 | 8648 | 8648,2 | 33,76 | 0,000 |
| Error | 8 | 2049 | 256,2 | ||
| Total | 9 | 10698 | |||
Fuente: Elaboración propia.
Conclusiones
Los análisis estadísticos mostraron que es mejor subcontratar procesos de manufactura de las piezas que se necesitan para fabricar subpartes. Debido a que en las fábricas no es posible realizar el ciento por ciento de la subcontratación por razones de calidad, entre otras, se ha creado en el presente trabajo un indicador que ayuda a decidir en caso de que solo sea posible subcontratar un conjunto de fabricación de las subpartes. Este indicador fue la penalización, fórmula que depende de los pedidos y de los estándares que se manejen, de acuerdo con las piezas para fabricar subpartes. Se ha mostrado cómo se utiliza el indicador de penalización, que puede ser un soporte para la toma de decisiones.
Una comparación de medias mediante el ANOVA ha permitido elegir qué versiones son más favorables a la hora de tomar las decisiones sobre qué conjuntos de partes subcontratar. Se han mostrado dos versiones pull, pero se pueden realizar muchas más combinaciones, que los empresarios pueden explorar, a partir de estos ejemplos.
Aunque las versiones de los procesos actuales sean pull o híbridos entre push y pull, se ha mostrado una alternativa de cómo mejorar procesos a través de subcontratación y un indicador que ayuda a tomar la decisión; si un proceso es ciento por ciento pull, la subcontratación ayudará a mejorar la versión de la configuración productiva.
Dos alternativas para continuar y mejorar esta propuesta incluyen los contextos multivariados y los híbridos de versiones push-pull. En la primera alternativa, se puede ver la penalización y el tiempo como variables en un contexto multivariado y plantear un modelo que incluya una distribución de probabilidad multivariada; esta propuesta ayudaría a que la metodología sea más rigurosa y que considere correlaciones entre variables. Otro segundo aspecto multivariado que se puede tener en cuenta es la comparación de las versiones de fabricación consideradas como alternativas y la versión actual del proceso. En este segundo aspecto, se pueden estimar análisis de varianzas multivaria-dos (MANOVA, por siglas en inglés) en lugar de un ANOVA, y preferir otras variables de interés, tales como desperdicios de material y consumo de energía. Un tercer aspecto multivariado sería mejorar la fórmula de penalización con una que considere más variables, con el fin de que la metodología sea cada vez más universal. En la segunda alternativa, se pueden contemplar híbridos de versiones push-pull en más detalle y hacer propuestas sobre versiones combinadas que satisfagan las condiciones de distintas empresas, en especial, las que no tienen configurado su proceso productivo con una filosofía completamente push o pull.