Introduction

Optical communication systems based on multi-carrier transmission are a promising solution to face the ever-growing demand for data traffic since they permit an increment of data rate per channel using multiple carriers (also called sub-carriers), resulting in high spectral efficiency [¹, ²]. Nevertheless, the development of these types of systems poses challenges such as the efficiency of algorithms based on digital signal processing (DSP), development of gridless devices (in spectral terms), and supporting software-defined optical transmission [², ³].

Nyquist Wavelength Division Multiplexing (Nyquist-WDM) technology has been proposed for implementation in optical gridless or flexible-grid systems [⁴] because its bandwidth is equal to the symbol rate with an ideal rectangular shaped spectrum. But, in practice, a perfect rectangular spectrum is not possible because infinite duration sinc-shaped pulses are required. Therefore, practical optical bandwidth is wider than Nyquist bandwidth. This is called the roll-off factor, which generates an inevitable interchannel interference (ICI), increasing the bit error rate (BER) even in back-to-back (B2B) scenarios [⁵, ⁶]. The roll-off factor is a dimensionless value between zero and one in the root-raised-cosine (RCC) function. Fig. 1 1 shows the impact of the roll-off factor in the temporal domain and optical domain, respectively. There is a proportional relation between the roll-off factor and the ICI reflected as optical signal-to-noise ratio (OSNR) degradation when frequency channel spacing is attempted to be lower than the baud rate or the roll-off factor is greater than zero .

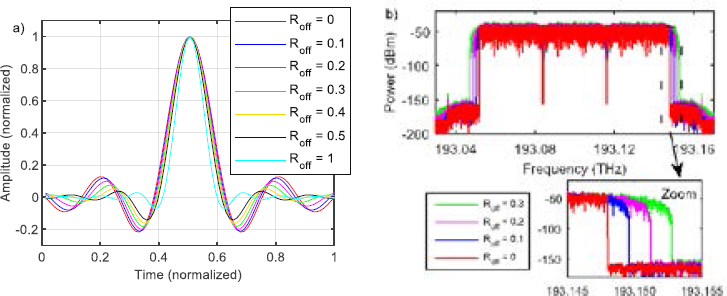
Fig. 1. a) nyquist pulses for different roll-off factors (Roff); b) optical spectrum for different roll-off factors (Roff) [⁷]. 

Additionally, in standardized wdm grids, ICI has been understood as a nonlinear effect of the optical fiber due to high launch power and its variation in adjacent channels [⁸]. Principal nonlinearities produced by the Kerr effect in multichannel transmission are cross-phase modulation (XPM), self-phase modulation (SPM), and four-wave mixing (FWM). These nonlinearities depend on chromatic dispersion directly or indirectly as well as power intensity [⁹].

In summary, the causes of ICI can be listed according to network devices: laser, digital pulse-shaping filter and optical fiber nonlinearities (see Table 1).

Thus, the two contributions of ICI due to both spectral overlap among adjacent channels and high launch power are a significant issue in optical gridless links, where sub-Nyquist channel spacing for spectral efficiency increment is attempted.

On the one hand, crosstalk due to nonlinear optical impairments has been widely studied in fixed-grid systems (WDM standard) as well as its mitigation by using different techniques such as scrambling the laser phase in the transmitter at a frequency much larger than the laser’s linewidth [¹⁰], Offset-QAM modulation [¹¹], equalization based on maximum likelihood sequence detection (MLSD) [¹²], chromatic dispersion compensation techniques along with digital backpropagation algorithm [¹³], and adaptative equalization based on Kalman filtering and maximum likelihood estimation (MLE) [¹⁴].

On the other hand, in a gridless scenario with sub-Nyquist spacing, several techniques have been studied to minimize/mitigate the ICI effects based on mostly complex dsp, for instance, by using frequency-diversity MIMO (multiple-input multiple-output) techniques [¹⁵], or by using pre-distortion on the transmitter side to emphasize the high frequency components of the transmitted signal, getting an optical spectrum closer to the ideal rectangular-shaped spectrum supported by linear equalization on the receiver side [¹⁶]. Besides, processing at the bit-data level with Kobayashi coding was proposed in [¹⁷], while an approach using independent SISO (single-input single-output) linear equalizers together with FEC (forward error correction) was proposed in [⁶]. Recently [¹⁸], nonsymmetrical demodulation has been demonstrated as one technique to reduce BER in multicarrier systems under ici. Additionally, an all-optical method for ICI mitigation has been proposed in [¹⁹], avoiding the use of multi-channel detection.

Nevertheless, the assumption that both ICI contributions (due to overlap and high launch power) could have a predictable behavior cannot be made because sequence randomness and channel power variation induce an interaction among optical overlapped channels during transmission. Thus, a characterization of the ICI effects in a gridless scenario under power variations should be made.

In this work, we analyze and characterize ICI in a gridless Nyquist-wdm system with coherent detection, modeled in VPItransmissionMaker™ software, compensating dispersion and nonlinearities with asymmetrical digital backpropagation (DBP). This manuscript is an extension of the conference paper [²⁰] that adds an extensive analysis of nonlinear impact, including new scenarios with 16QAM modulation format, dual polarization and at 32 Gbaud. We evaluate the ICI effects in terms of BER as functions of optical system parameters such as frequency channel spacing, roll-off factor of the digital Nyquist filter, launch power and laser linewidth.

The remainder of this manuscript is organized as follows: Section 2 describes the simulation setup of the Nyquist-WDM system; ICI characterization for scenarios under linear and nonlinear effects, including nonlinear equalization, is discussed in Section 3; and finally, conclusions are presented in Section 4.

System Configuration

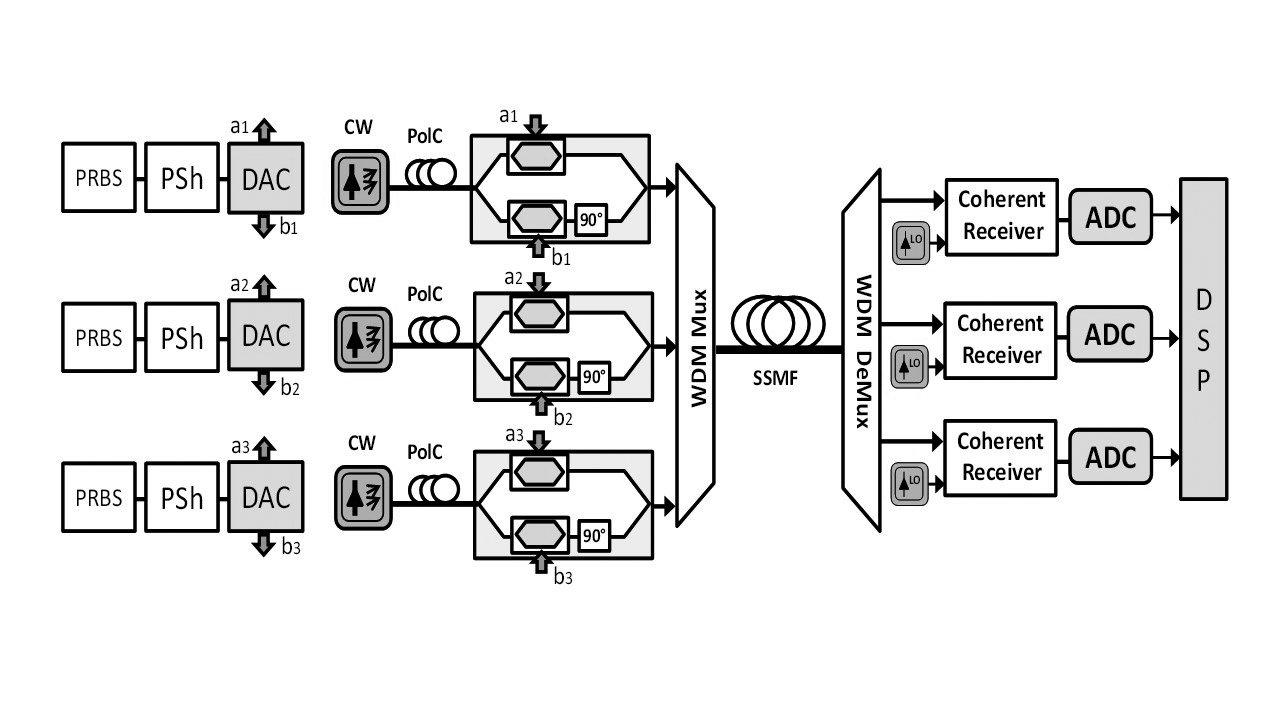
A 3 x 16/32 Gbaud Nyquist-WDM system working with QPSK and 16QAM modulation format (see Fig. 2) is simulated using VPItransmissionMaker™, in b2b and for transmission distances up to 250 km. An in-phase and quadrature (IQ) modulator is driven using a digital-to-analog converter (DAC) where the pseudo-random binary sequence (PRBS) is generated with length of 2¹⁶. Besides, pulse-shaping (PSH) is carried out by a digital filter with the RRC function evaluated in a typical roll-off factor of 0.1, but in some cases, it is switched from ~0 to 0.5. The optical source of each transmitter is a continuous wave (CW) laser with linewidth of 10 kHz. The central one transmits at 1550 nm. Launch power per channel is between -5-16 dBm, measured at fiber input. A polarization controller (POLC) is included, and QPSK modulations and 16QAM formats are performed with a pair of single drive Mach-Zehnder modulators (MZM) for an iq configuration. Signals are transmitted into a standard single-mode fiber (SSMF), with an attenuation of 0.2 dB/km, dispersion factor of 16 ps/(km-nm), and nonlinear index of 2^-20 m²/W.

Fig. 2. Simulation set-up of a Nyquist-WDM system modeled in VPItransmissionMaker™. 

The ideal coupler is used as a flexible multiplexer. On the receiver side, and ideal demultiplexer (no losses, rectangular spectral response and bandwidth equal to the channel bandwidth) with flexible grid is utilized. Optical demodulation is carried out with three independent coherent detectors. The coherent receiver is based on a 90° hybrid coupler and two balanced photodiodes with a responsivity of 1. The local oscillator (LO) of the coherent receiver is a laser with the same characteristics as those used as an optical source on the transmitter side.

Analog-to-digital conversion (ADC) is performed after coherent detection. A matched filter (MF) separates electrically each channel by using the RRC function too. dsp algorithms are implemented by co-simulation with Matlab™. Firstly, the chromatic dispersion is compensated using a transversal filter by means of the Fourier transform of the inverse fiber dispersion function. Then, nonlinearities are minimized by using an asymmetrical digital backpropagation algorithm [²¹-²⁴] according to the system (single [²¹] or dual polarization [²²] case), and the clock recovery module carries out signal synchronization before phase correction. Finally, demodulation is performed, and the BER is estimated.

Simulation Results and Discussion

ICI characterization in terms of BER is carried out under variation of system parameters on three stages. Section 3.1 shows the ICI impact for two scenarios, i) linear (L): switching off nonlinear contributions in the optical fiber module of VPITransmissionMaker, and ii) nonlinear (NL): regular ssmf module. Section 3.2 explains the ICI impact with and without nonlinear equalization based on the DBP algorithm at 16-Gbd QPSK transmission. Finally, Section 3.3 shows the same evaluation as in Section 3.2 for 32-Gbd dual-polarization 16QAM systems.

ICI impact due to linear and nonlinear fiber optic effects

In Fig. 3, the BER is estimated as a function of the launch power for 100 km transmission distance. It can be noticed how for values higher than 5 dBm, launch power increases the BER up to 2 orders of magnitude for a channel spacing of 17.6 GHz. For a channel spacing of 16 GHz, the BER increases up to 1 order of magnitude. For a channel spacing of 15.5 GHz, the BER variation is low because the overlapping penalty is already high (BER higher than 3 x 10^-2). Hence, it is observed that penalty in BER due to overlapping is around 4 orders of magnitude (channel spacing of 17.6 vs. 16 GHz). Besides, under an optical fiber with nonlinear impairments, the increment of power from 5 to 10 dBm has an impact on BER of up to 2 orders of magnitude. This first evaluation notes that, for the received signal, spectral channel overlapping is more harmful than power increment.

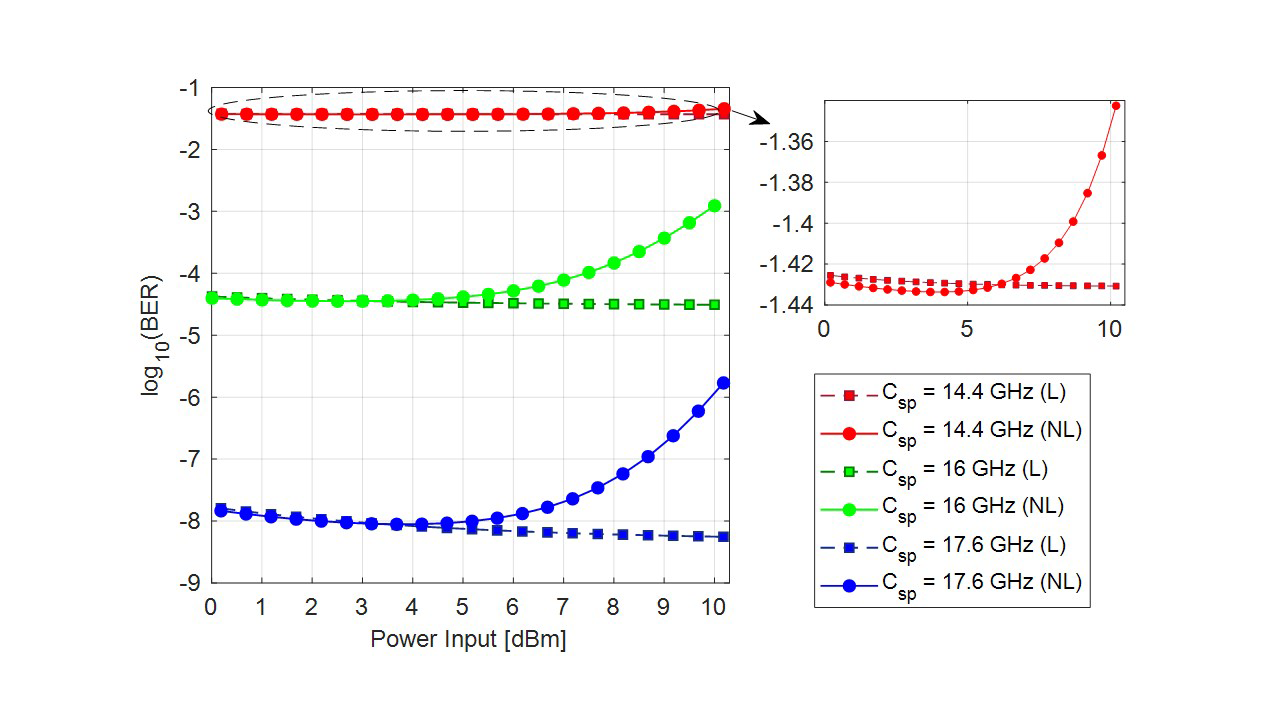
Fig. 3. BER vs. launch power for different channel spacings for QPSK at 16 Gbaud. Two cases explored: link affected by i) only linear (L) effects, and ii) linear plus nonlinear (NL) effects. 

Fig. 4 shows BER vs. roll-off factor for a launch power of 9 dBm. The difference in BER between linear effects and linear plus nonlinear effects is higher for roll-off values lower than 0.2. For a channel spacing of 17.6 GHz, nonlinear impairments have an impact of 5 orders of magnitude for a roll-off of 0.1, whilst for a channel spacing of 16 GHz, the penalty in BER is close to 2 orders of magnitude. Comparing these results with Fig. 3, it is also evidenced that the ICI impact for overlapped channels is higher than the impact of nonlinear effects. A small difference in BER (~0.1 orders of magnitude) between the linear and nonlinear cases is observed for a channel spacing of 14.4 GHz. Besides, roll-off affects the BER close to the nonlinear impairments impact. It is noticed that for a roll-off of 0.5, the difference in BER for the three channel spacings is significantly reduced. This is because channel bandwidth is broader and, therefore, channels are more overlapped.

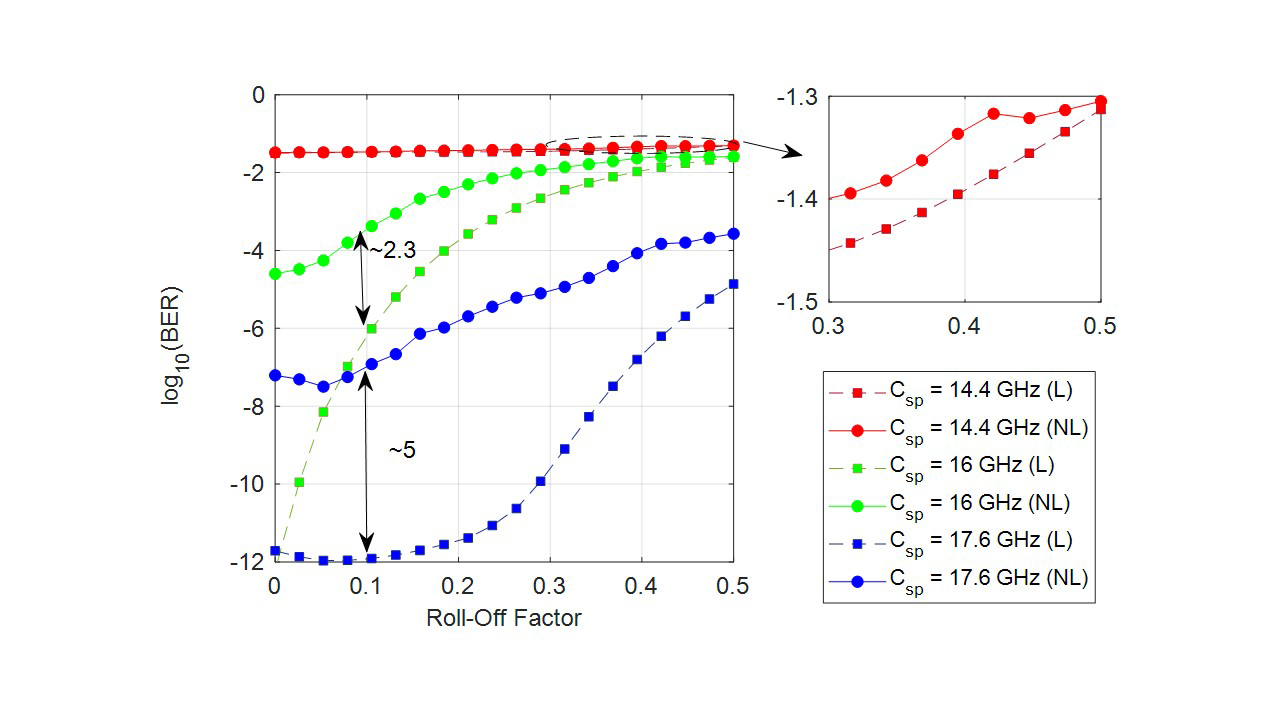
Fig. 4. BER vs. roll-off factor for different channel spacings in QPSK at 16 Gbaud. Two cases explored: link affected by i) only linear (L) effects, and ii) linear plus nonlinear (NL) effects. 

Fig. 5 shows that nonlinear impairments induce an increase in BER of 3 orders of magnitude when channels are overlapped with a channel spacing of 16GHz (green lines), even for short distances (from 20 km). Since launch power is 9 dBm, attenuation does not have a high impact on distances shorter than 100 km. Moreover, chromatic dispersion is fully compensated at the dsp-based receiver. Thus, for a channel spacing of 17 GHz (no overlap), error-free transmission can be achieved.

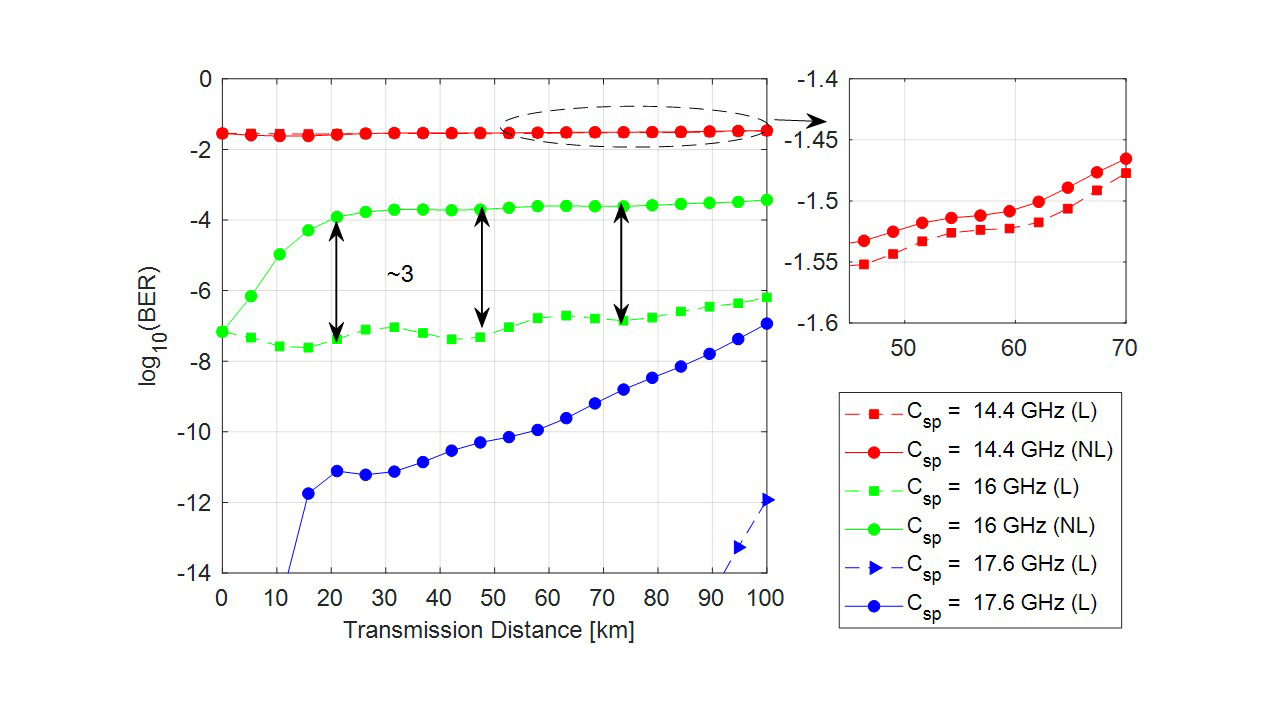
Fig. 5. BER vs. transmission distance for different channel spacings in QSPK at 16 GBaud. Two cases explored: link affected by i) only linear (L) effects, and ii) linear plus nonlinear (NL effects. 

Table 2 summarizes the results presented in this subsection.

ICI impact due to nonlinear mitigation by using DBP in QPSK at 16 Gbaud

Performance is evaluated in sub-Nyquist, Nyquist and quasi-Nyquist channel spacings (at 15.5, 16 and 16.5 GHz, respectively). Fig. 6 shows BER vs. launch power for a transmission distance of 210 km. The best performance in the system is obtained for launch powers of 8 dBm in all channel spacings under evaluation. Due to attenuation, BER decreases as launch power increases. Nevertheless, it is evidenced that after 8 dBm, the BER grows due to nonlinear impairment stimulation.

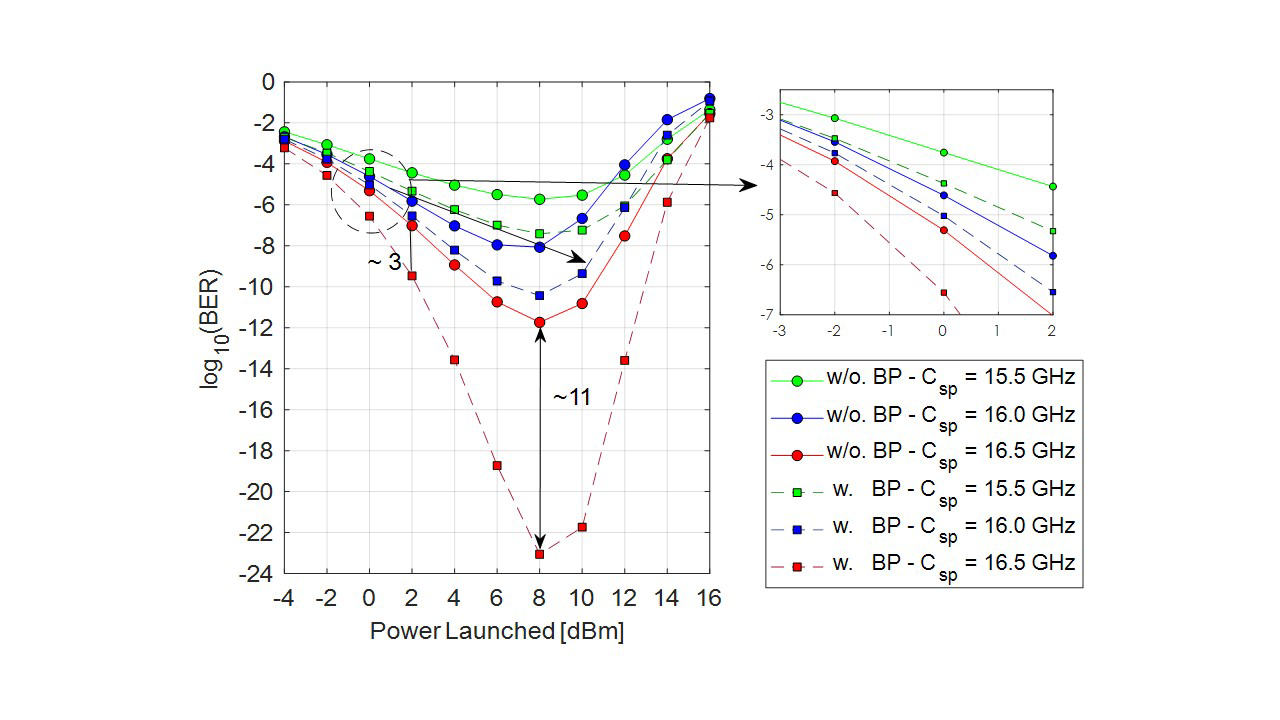
Fig. 6. BER vs. launch power for different channel spacings including nonlinear mitigation in QPSK at 16 Gbaud with (w) and without (w/o) backpropagation (BP) algorithm. 

Moreover, by using DBP, a gain of 11 orders of magnitude is achieved in the quasi-Nyquist channel spacing case as observed in the vertical double arrow in the plot. In the Nyquist channel spacing case (16 GHz), by using DBP, it gains up to 2 orders of magnitude, whereas in the sub-Nyquist spacing gains are around 1 order of magnitude. It means that DBP cannot mitigate ICI due to overlapping, and the gain is due to nonlinear equalization of optical fiber impairments.

In Fig. 7, BER vs transmission distance curves are shown for launch power of 14 dBm. For sub-Nyquist and Nyquist cases, DBP shows an improvement of 0.6 and 1 order of magnitude, respectively. In the quasi-Nyquist case, DBP performance is better, for 210 km transmission length, DBP reduces the ICI impact on BER by approximately 3.5 orders of magnitude.

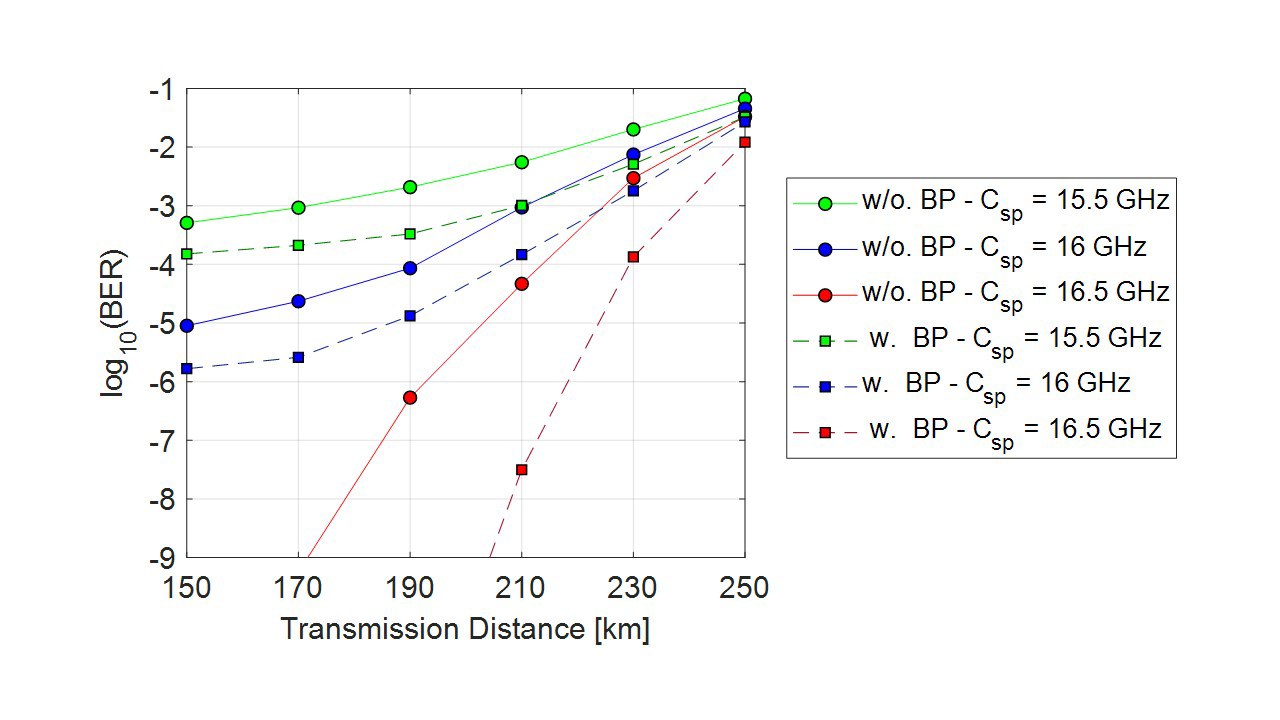
Fig. 7. BER vs. transmission distance for different channel spacings, including nonlinear mitigation in QPSK at 16 Gbaud with (w) and without (w/o) backpropagation (BP) algorithm. 

Fig. 8 shows BER vs. roll-off factor curves for a transmission distance of 100 km and launch power of 14 dBm. As mentioned, the roll-off factor highly impacts the ICI effects, measured in terms of BER due to bandwidth broadening in the optical spectrum. For sub-Nyquist channel spacing, with a typical roll-off factor of 0.1, DBP reduces the BER approximately by 2.5 orders of magnitude. DBP can minimize the ICI effects, increasing the roll-off factor up to 0.12 for the sub-Nyquist and Nyquist cases. In the quasi-Nyquist case, DBP can minimize the ICI effects for roll-off factors from 0.35 to 0.45. It entails system computational complexity reduction.

Fig. 8. BER vs. roll-off for different channel spacings, including nonlinear mitigation in QPSK at 16 Gbaud with (w) and without (w/o) backpropagation (BP) algorithm. 

Fig. 9 shows system performance for several values of laser linewidth, spectral channel spacings of 15.5 GHz, 16 GHz and 16.5 GHz in 100 km of transmission distance and launch power of 14 dBm. Laser linewidth lower than 10^-4 Hz does not show significant impact on the BER because phase noise stimulation and chromatic dispersion are moderately low. Nevertheless, the linear plus nonlinear effect can be reduced by ~4 orders of magnitude in terms of BER using the DBP.

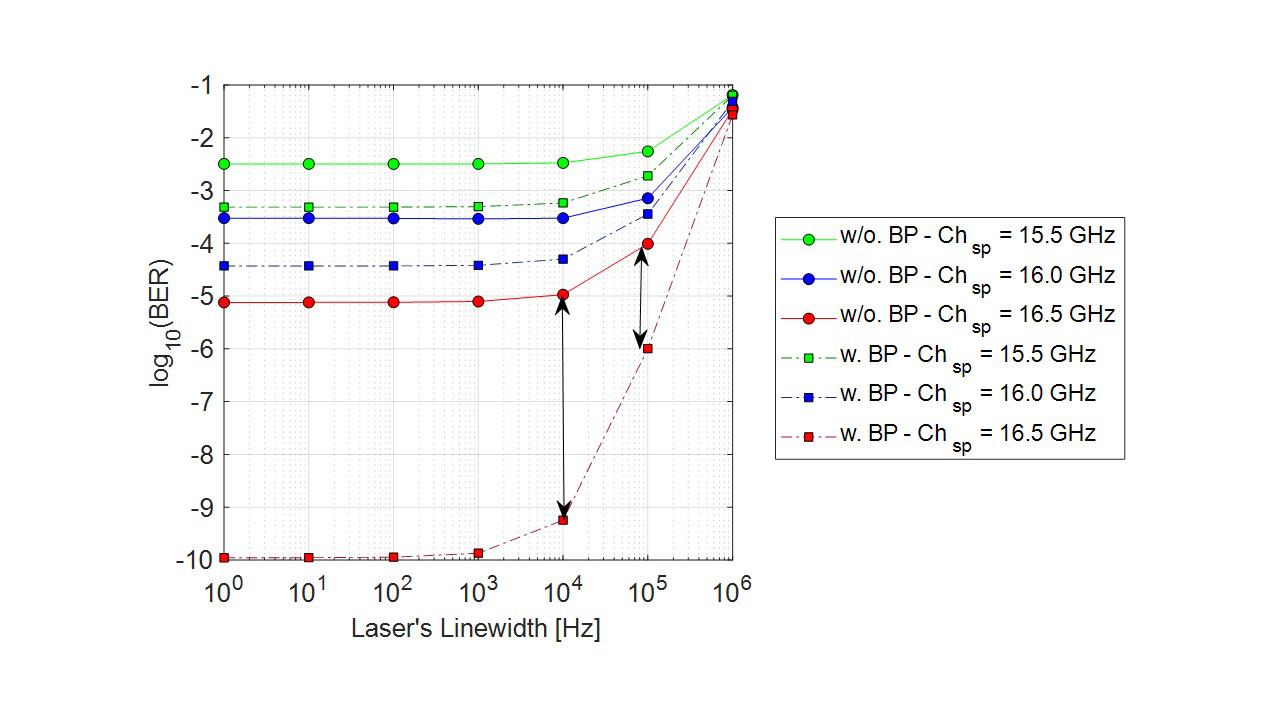
Fig. 9. BER vs. laser linewidth for different channel spacings, including nonlinear mitigation in QPSK at 16 Gbaud with (w) and without (w/o) backpropagation (BP) algorithm. 

Finally, Fig. 10 shows the ER vs. channel spacing curves for a transmission distance of 100 km and launch power of 2, 8, and 14 dBm. Nonlinear ICI degrades system performance when launch power is higher than 8 dBm (see red line with circles in Fig. 10). Nevertheless, when DBP is used, system performance improves significantly, even in sub-Nyquist cases (see the 8 dBm curve in Fig. 10).

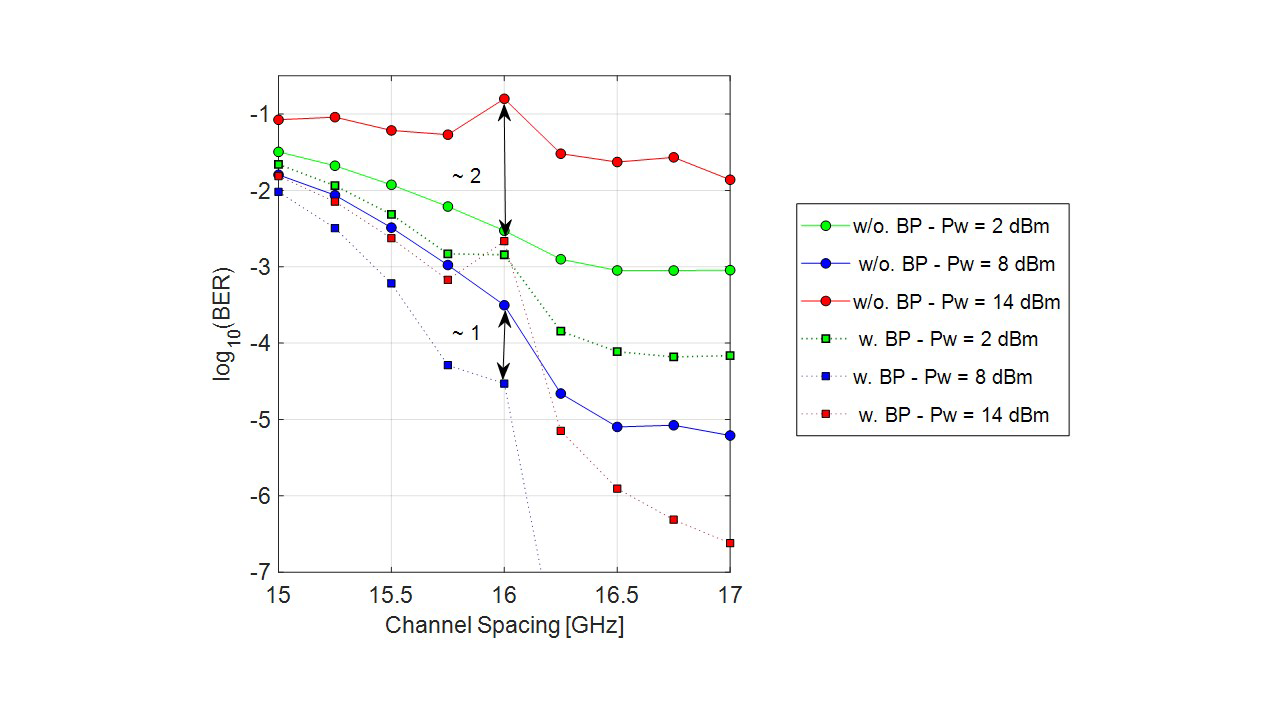
Fig. 10. BER vs. channel spacing for different launch powers, including nonlinear mitigation in QPSK at 16 Gbaud with (w) and without (w/o) backpropagation (BP) algorithm. 

Table 3 summarizes the results presented in this subsection.

ICI impact due to nonlinear mitigation by using DBP in 16QAM at 32 Gbaud

Regarding Fig. 11, the increment of optical power per channel above ~0 dBm has high impact in terms of BER due to fiber nonlinearities in 80 km. However, digital mitigation of these effects improves system performance even for the Nyquist and sub-Nyquist channel spacing cases. At 2 dBm, for a channel spacing of 36 GHz, the highest gain in terms of BER is noticed in this case. In comparison with QPSK modulation format with half baud rate and single polarization, the impact on BER in this case is seen even for launch powers from 0 dBm.

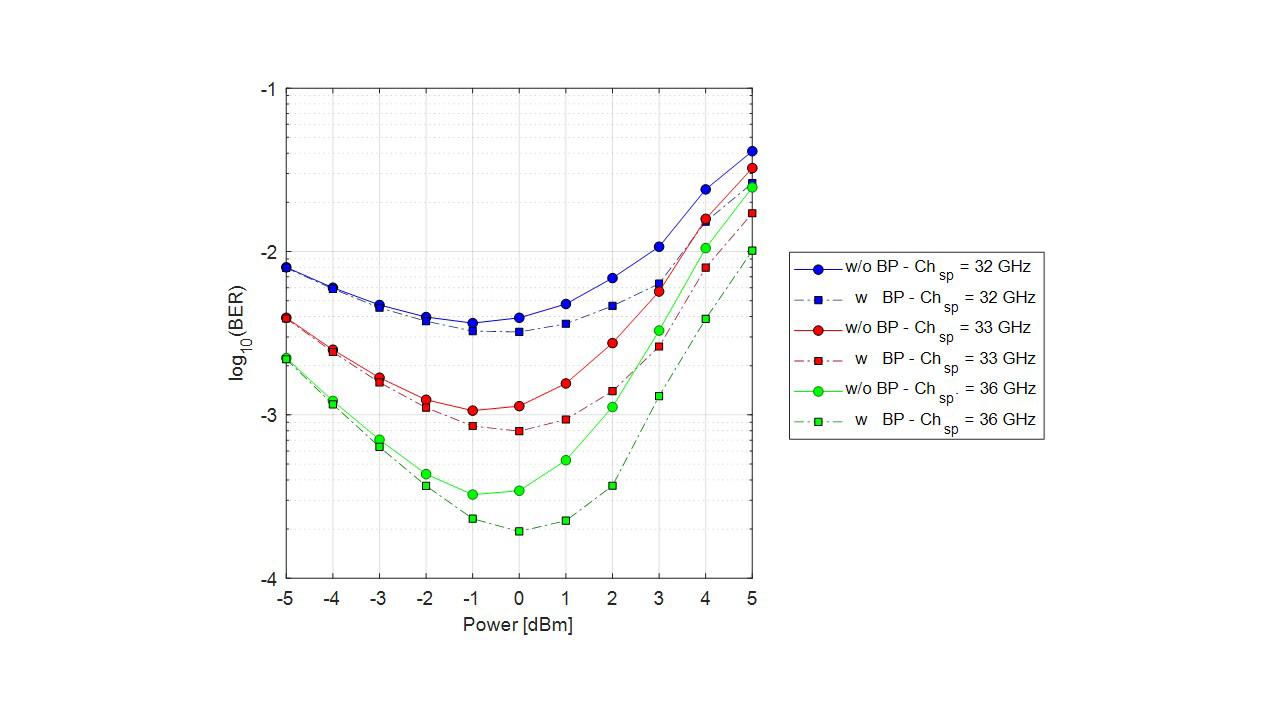
Fig. 11. BER vs. launch power for different channel spacings, including nonlinear mitigation in 16QAM at 32 Gbaud with (w) and without (w/o) backpropagation (BP) algorithm. 

Fig. 12 shows BER vs. transmission. With Nyquist spacing (32 GHz), the gain in BER using DBP is only ~0.4 orders of magnitude. Comparing with the QPSK scenario, it is worth mentioning that the capacity is increased 4 times in this case (16 Gbd vs. 32 Gbd and single polarization vs. dual polarization). Hence, when channels are overlapped, the interaction of symbols transmitted at the same frequency component is more drastic, inducing a BER increment. Besides, the gain using DBP is higher with shorter distances (see at 50 km in terms of BER). For 33 GHz, it is possible to reduce the BER by 1 order of magnitude, decreasing the span length by 45 km (from 120 to 75 km). However, the ICI impact due to spectral overlapping significantly reduces the gain of the nonlinear equalizer because the noise floor is higher (BER values higher than 10^-3). Moreover, for 80 km and longer transmission distances, reduced channel spacing and nonlinear effects affect the equalizer performance. Nevertheless, a penalty reduction of ~15 km (from 80 to 65 km) is reached.

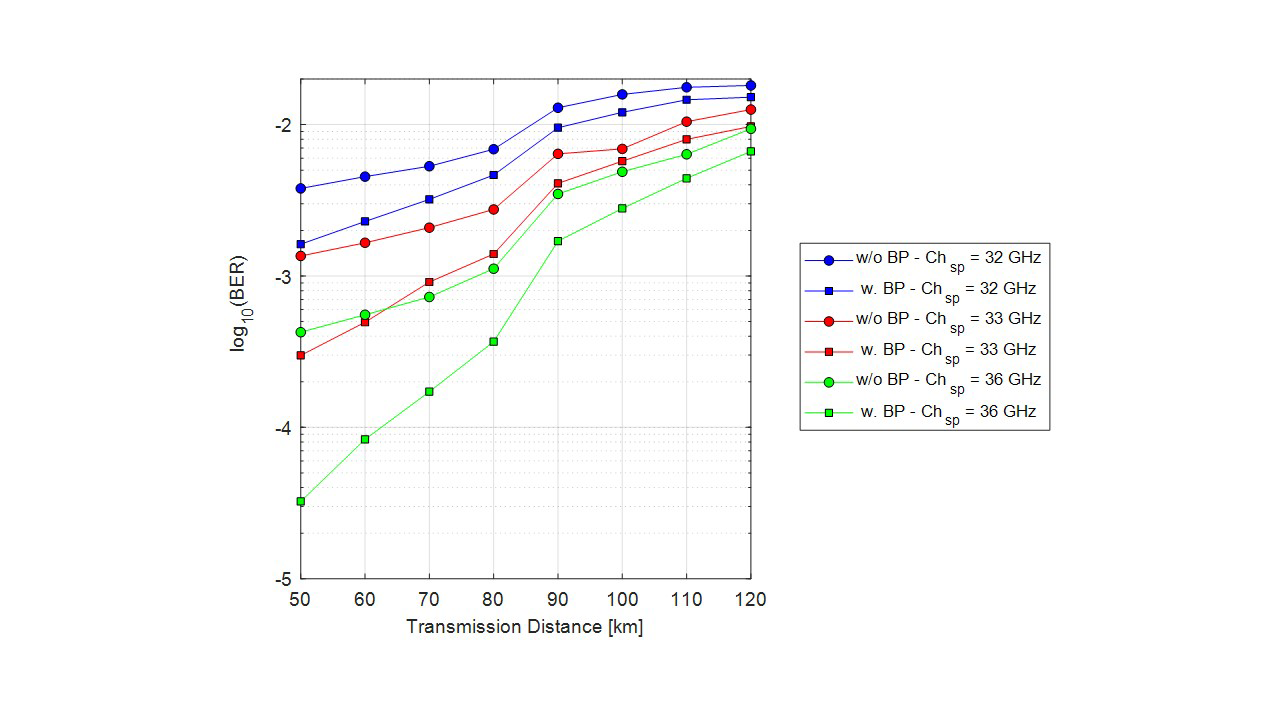
Fig. 12. BER vs. transmission distance for different channel spacings, including nonlinear mitigation in 16QAM at 32 Gbaud with (w) and without (w/o) backpropagation (BP). 

Fig. 13 shows BER vs roll-off factor curves for a transmission distance of 80 km. For channel spacing of 32 GHz (Nyquist) and 33 GHz (sub-Nyquist), roll-off factor variations do not significantly modify the BER. However, for a channel spacing of 36 GHz, 1 order of magnitude of BER can be reduced with an increment of a rolloff factor from ~0.1 to ~0.3.

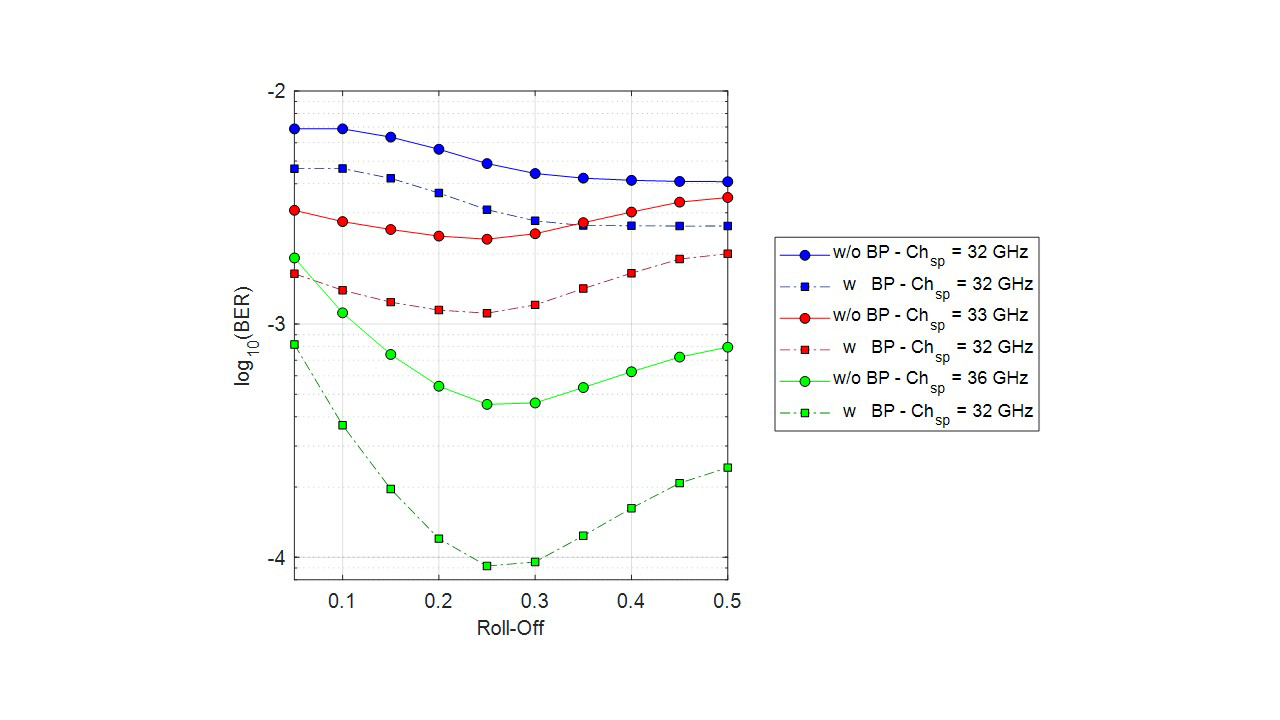
Fig. 13. BER vs. roll-off for different channel spacing including nonlinear mitigation in 16QAM at 32 Gbaud with (w) and without (w/o) backpropagation (BP). 

Furthermore, as in the single-polarization QPSK case, laser linewidth values up to 1 MHz do not have a significant impact on the BER (see Fig. 14 for a transmission distance of 80 km). The use of DBP can reduce the impact on BER, especially when channel spacing is increased as seen at 36 GHz of channel spacing.

Fig. 15 shows BER vs channel spacing curves for powers per channel of 0, 1.5 and 3 dBm in 80 km of transmission distance. By using a channel power of 0 dBm, the best performance is obtained in terms of BER. A channel spacing reduction of 0.5 GHz is possible at a BER of 2.7×10^-2. Moreover, a channel spacing reduction of 2.5 GHz increases the BER approximately in 1 order of magnitude when non-linearities are mitigated, in scenarios of ~3 dBm of optical power per channel.

Fig. 14. BER vs. laser linewidth in 16QAM at 32 Gbaud with (w) and without (w/o) backpropagation (BP). 

Table 4 summarizes the results presented in this subsection as function of the BER.

Conclusions

We researched into the impact of the ICI effects on Nyquist-WDM systems at 16 and 32 Gbaud for both QPSK and 16QAM modulation. The spectral separation between adjacent modulated carriers was reduced as much as possible, even under the baud rate in Hz (sub-Nyquist separation), leading to spectral overlapping. The ICI effects were characterized in terms of the BER as a function of several system parameters such as channel spacing, rolloff factor, laser linewidth and launch power. Despite its high value, launch power of 8 dBm showed the best performance for sub-Nyquist cases in QPSK. For the 16QAM scenario, the gain was lower than 1 order of magnitude because the systems had a 4-time higher capacity.

It was demonstrated that the impact in the BER is much higher when channels are overlapped than when affected by nonlinear effects due to high launch powers. Besides, the DBP-based equalizer cannot mitigate impact due to overlapping since this effect does not depend directly on optical fiber impairments; however, an improvement in the BER can be achieved. The use of the DBP algorithm can relax the system complexity by means of the rolloff factor penalty reduction for different channel spacing cases. Ffor transmission distances shorter than 210 km, the DBP can reduce the BER in more than 1 and 3 orders of magnitude for typical rolloff factor values in QPSK and 16QAM, respectively. Moreover, it was confirmed that laser linewidth does not stand a significant penalty for values lower than 10 kHz under nonlinearities effects.

Finally, DBP equalizers may improve the multicarrier spectral efficiency by allowing moderate levels of ICI in nonlinear scenarios affected by high launch power variations. These equalizers integrated with ICI mitigation techniques designed for gridless scenarios with low computational complexity is a challenging future work.

Acknowledgements

This work was partially supported by the PhD Grant 567 of Colciencias.This work is also associated with the program “Reconstrucción del Tejido Social en Zonas de Posconflicto” and particularly with the project “Modelo Ecosistémico de Mejoramiento Rural y Construcción de Paz: Instalación de Capacidades Locales”, financed by the Fondo Nacional de Financiamiento para la Ciencia, la Tecnología y la Innovación, Fondo Francisco José de Caldas contract number 213-2018 and code 58960.