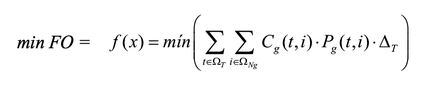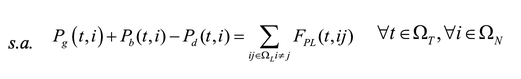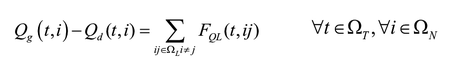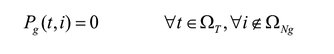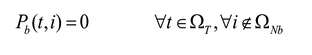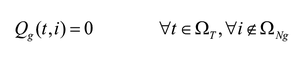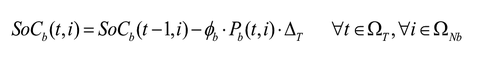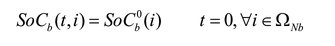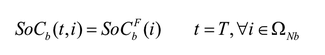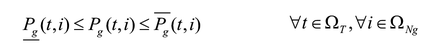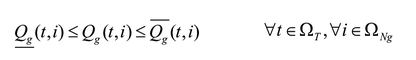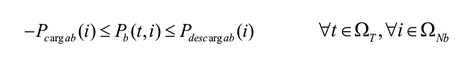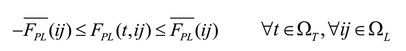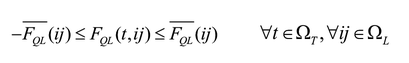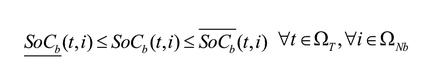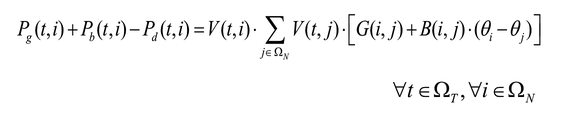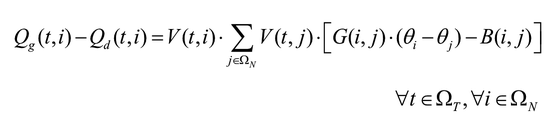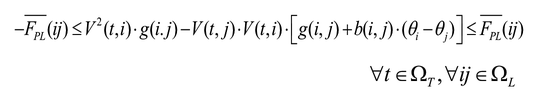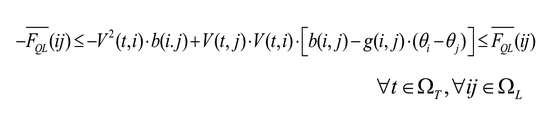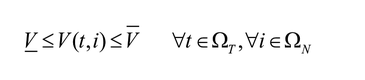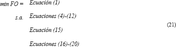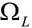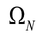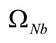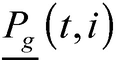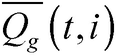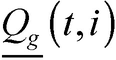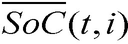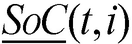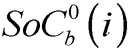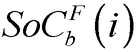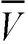Introducción
Los sistemas de distribución tienen como objetivo principal entregar la energía que proviene de los sistemas de transmisión o subtransmisión a los usuarios finales, y su operación se ha enfocado en garantizar criterios de calidad, confiabilidad y continuidad del servicio, al menor costo posible. Sin embargo, en los últimos años han aparecido diversos elementos que afectan los aspectos operativos tradicionales. Uno de estos son los almacenadores de energía, los cuales, a pesar de afectar dicha operación, proporcionan una gran variedad de beneficios para los operadores de red.
El uso de almacenadores genera mejoras significativas económicas y operativas, entre las que se destacan menores potencias transportadas por las líneas de transmisión, menores pérdidas de energía, mejores niveles de tensión y aplazamiento de los proyectos de expansión en el tiempo. Adicionalmente, afectan las curvas de carga del sistema, ya que permiten almacenar energía en periodos de baja demanda e inyectarla en periodos de alta carga. Este comportamiento ocasiona una corrección de la curva de carga por la disminución de los picos de demanda del sistema, lo que se refleja en un alivio en la cargabilidad de los elementos de la red.
El uso de estos elementos resulta de gran interés para los operadores de red debido a la disminución de su costo, el avance de nuevas tecnologías y los beneficios económicos y operativos que generan, por lo que se han convertido en una nueva y atractiva alternativa de inversión. Gracias a las ventajas que presentan, en los últimos años se han realizado diversos trabajos, entre los que se destacan las siguientes referencias.
En [1] se plantea una operación óptima de los almacenadores de energía en sistemas de distribución con generación eólica utilizando una función multiobjetivo, en la cual uno de los objetivos es minimizar el costo de compra de energía eléctrica. Esto se soluciona usando un algoritmo genético. En [2] se propone un modelo matemático que plantea el aplanamiento de la curva de carga, usando almacenadores de energía, y cuyo objetivo es disminuir las pérdidas de energía eléctrica. En [3] se plantea un modelo con varias funciones objetivo que permita satisfacer las necesidades de un operador de red; en este modelo utilizan un flujo de carga trifásico desbalanceado con almacenadores de energía y generación solar para operar de forma óptima los sistemas de distribución.
En [4] se presentan diversas estrategias para utilizar el despacho económico con almacenadores de energía en sistemas de distribución. Para su solución los autores proponen un modelo de optimización basado en la operación de almacenadores de energía en coordinación con energías renovables y variaciones de carga. En [5] se realiza un despacho económico de un sistema con energías renovables y almacenadores de energía. Emplean un modelo matemático lineal que es resuelto utilizando un software de optimización comercial. En [6] se propone un modelo no lineal entero mixto para encontrar la operación óptima de los almacenadores de energía en un sistema de distribución con generación solar. Este problema tiene dos funciones objetivo: el costo de compra de energía y costos ambientales por emisiones de gases. Este problema es resuelto utilizando el software de optimización comercial gams.
En [7] se propone una metodología para minimizar el costo de pérdidas de energía eléctrica en sistemas de distribución, se utiliza un modelo no lineal que se resuelve con el uso del software de optimización comercial gams. En [8] se plantea una metodología para operar de forma coordinada los almacenadores de energía en sistemas de distribución. En esta metodología los almacenadores mejoran la flexibilidad y eficiencia de la operación de los sistemas de distribución. En [9] proponen una metodología que analiza los impactos económicos de los almacenadores de energía en los sistemas de distribución para poder generar compensaciones por parte del Gobierno y de los operadores de red para los inversionistas privados.
En [10] se propone una estrategia de aplanamiento de la curva de carga mediante el uso de almacenadores de energía y cuyo objetivo es mejorar la confiabilidad y capacidad del sistema. En [11] se usa un modelo probabilístico de una red neuronal para predecir la curva de demanda y generación fotovoltaica para carga y descarga de los almacenadores de energía, con lo cual se obtiene una curva de carga aplanada. En [12] se desarrolla una metodología que permita a los operadores de red manejar los picos de demanda mediante la operación coordinada de almacenadores de energía.
En [13] se presenta una estrategia de control de carga y descarga de los almacenadores de energía en sistemas de distribución, con el fin de mejorar el valor de compra de la energía en el mercado eléctrico. Por su parte, [14] proponen una coordinación óptima de almacenadores de energía en sistemas de distribución con generación distribuida para tener una operación segura y flexible de la red de distribución.
A diferencia de los trabajos anteriores, este artículo propone una metodología para la compra y venta de energía con un adecuado manejo de la curva de carga haciendo uso de almacenadores. Así, pues, son propuestos dos modelos matemáticos (lineal y no lineal), cuya función objetivo es la minimización del costo de compra de la energía eléctrica. La metodología también considera el impacto en las pérdidas de energía en la red que abastece el sistema de distribución y proporciona una herramienta que puede ser aplicada en la operación y el planeamiento de sistemas de distribución con almacenadores de energía.
El primer modelo es lineal y considera la minimización de compra de energía, y está sujeto a un conjunto de restricciones técnicas y operativas. El segundo modelo es no lineal e incluye, además de lo anterior, la reducción de las pérdidas técnicas de la red; en este, el conjunto de restricciones es similar al del primer modelo. Para la solución de ambos modelos se emplea el software de optimización comercial gams.
Con esta metodología se proporciona una herramienta de toma de decisiones para la operación de sistemas de distribución que consideran elementos almacenadores de energía. Además de la disminución del valor de compra de energía y las pérdidas técnicas de la red, el uso de esta metodología permite mejorar la cargabilidad de las líneas de transmisión, así como diferir en el tiempo los planes de expansión del operador de red.
Metodología
Formulación del problema
El problema de la operación de sistemas de distribución con almacenadores de energía se presenta mediante dos modelos matemáticos (uno lineal y otro no lineal), los cuales se explican detalladamente a continuación.
Modelo lineal
El modelo matemático se presenta en las ecuaciones (1)-(15); en estas, la función objetivo por minimizar considera el valor de costo de compra de energía eléctrica (1). El conjunto de restricciones presentado en las ecuaciones (2)-(15) tiene en cuenta las características técnicas y operativas de la red, y de los almacenadores de energía.
Las ecuaciones (2) y (3) corresponden al balance de potencia activa y reactiva, y las (4)-(6) describen la existencia de las variables en los nodos. La ecuación (7) es el estado de carga del almacenador de energía b conectado al nodo i en el tiempo t. Las ecuaciones (8) y (9) representan el estado inicial y final de carga del almacenador b conectado al nodo i. Las ecuaciones (10) y (11) representan los límites de potencia activa y reactiva del generador g en el nodo i. La ecuación (12) es el límite de potencia activa de carga y descarga de los almacenadores de energía. Las ecuaciones (13) y (14) son los límites de capacidad de las líneas y la (15) son los límites de carga de los almacenadores de energía.
Modelo no lineal
Con el fin de involucrar las pérdidas técnicas de energía en el modelo presentado en las ecuaciones (1)-(15), se modifican (2), (3), (13) y (14). En (16) y (17) se plantean las ecuaciones de balance nodal de potencia activa y reactiva, y en (18) y (19) los flujos de potencia activa y reactiva por los tramos de red del sistema [16].
Las ecuaciones (2) y (3) son sustituidas por (16) y (17), respectivamente. En estas ecuaciones, dado que la diferencia angular θij entre dos nodos es pequeña (en radianes), se asume que cos θij ≈ 1 y sen θij ≈ θij, por lo que pueden ser escritas como sigue:
Las ecuaciones (13) y (14) son sustituidas por (18) y (19). Como en el caso anterior, se asume que la diferencia angular θij es pequeña, y las ecuaciones (18) y (19) son expresadas en función de voltajes nodales y parámetros de la red. Por lo tanto:
Asimismo, es necesario adicionar la ecuación (20), con el fin de incluir los límites de tensión de la red.
Considerando las ecuaciones anteriores, el modelo no lineal completo se presenta de la siguiente forma:
Metodología propuesta
La metodología propuesta puede ser observada en el diagrama de flujo de la Figura 1. Inicialmente se define el sistema de prueba considerando todos los datos que lo describen por completo. Luego se selecciona el tipo de modelo para formular matemáticamente el problema (lineal o no lineal). Más adelante, se modela el problema en el software gams. Finalmente, se ejecuta el software y se analizan los resultados obtenidos.
Aplicacion y resultados
Para verificar los modelos matemáticos propuestos, usan dos sistemas de prueba de 7 y 34 nodos, respectivamente [15]. Con el objetivo de realizar un análisis comparativo, en ambos modelos matemáticos se consideran dos casos de estudio: 1) sin almacenadores de energía y 2) con almacenadores de energía. Se considera una vida útil de los almacenadores de energía de 10 años y una tasa de interés del 10 %. Todos los casos de estudio fueron implementados en gams.
Sistema de prueba 1
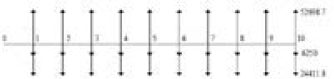
Este sistema tiene 7 nodos y se ilustra en la Figura 2, en la cual se muestra que la fuente está conectada en el nodo 1 y el sistema de almacenadores de energía está conectado en el nodo 2 (subestación). Los nodos 3-7 tienen demandas asociadas y la línea entre los nodos 1-2 representa el equivalente de Thévenin de la red conectada aguas arriba del nodo 2 (subestación). En este sistema el costo de los almacenadores de energía es de USD 250.000 y su costo anual de operación y mantenimiento, de USD 10.500.
Modelo lineal
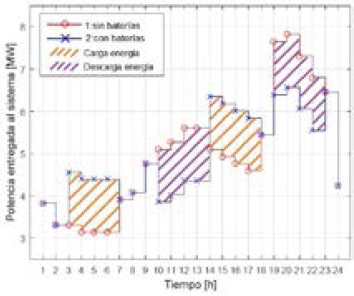
Al solucionar este modelo se obtienen los resultados presentados en la Tabla 1; en esta se observa que la situación más económica es aquella en la cual se usan almacenadores de energía (caso 2), con una utilidad diaria de USD 238,75 (USD 87.143,75 anuales). Las curvas de carga de ambos casos se presentan en la Figura 3, donde las líneas con círculos pequeños y líneas con x corresponden a los casos 1 y 2, respectivamente.
Tabla 1. Resultados del sistema de prueba 1, modelo lineal (USD)
|
Caso |
Función objetivo |
|---|---|
|
1 |
13.503,63 |
|
2 |
13.264,88 |
Fuente: elaboración propia.
La curva del caso 1 (líneas con o) es vista aguas abajo de la subestación, y la curva del caso 2 (líneas con x) es vista por la red aguas arriba de la subestación. La diferencia en energía entre las dos curvas de carga corresponde al ciclo de carga y descarga del almacenador de energía. De esta figura se obtiene un factor de carga de 0,64 para el caso 1 y de 0,76 para el caso 2, lo cual refleja una mejor distribución de la curva de carga del sistema; de esta manera, se obtiene una curva de carga más aplanada.
Respecto a la demanda máxima presentada en la hora 20, se aprecia que pasa de 7,81 mw en el caso 1 a 6,56 mw en el caso 2, y así se consigue una disminución de 1,25 mw. Esta reducción representa una mejora en la cargabilidad de los elementos del sistema y, por ende, un mejoramiento de las pérdidas de energía eléctrica de la red.
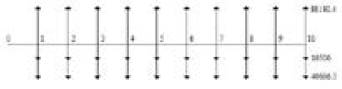
En la Figura 4 se presenta un diagrama de flujo con los costos anualizados, que incluye el costo del equipo, su mantenimiento y operación, así como la utilidad por compra y venta de energía. Con base en lo anterior, el costo anualizado del almacenador es de USD 40.686,3. En la figura se evidencia que la ganancia anual (diferencia entre utilidad y costo de inversión, operación y mantenimiento) es de USD 35.957,5.
Modelo no lineal
Con el propósito de incluir en el modelo matemático el efecto de las pérdidas de energía aguas arriba de la subestación, se usa el equivalente de Thévenin. De esta forma, se incluye en el análisis de forma aproximada el efecto de las pérdidas de energía durante las horas del día, así como también el valor de las pérdidas en la hora pico. En la Tabla 2 se presentan los resultados de la función objetivo del modelo no lineal, para ambos casos de estudio.
Tabla 2. Resultados del sistema de prueba 1, modelo no lineal (USD)
|
Caso |
Función objetivo |
|---|---|
|
1 |
13.619,98 |
|
2 |
13.378,39 |
Fuente: elaboración propia.
En la Tabla 2 se observa que los valores obtenidos con el modelo no lineal son mayores que los obtenidos con el modelo lineal, por causa del efecto de las pérdidas; asimismo, que el caso más económico es el que usa almacenadores de energía (caso 2), con una utilidad diaria de USD 241,59 (USD 88.180,4 anuales). Este valor es mayor al del modelo lineal debido al efecto de las pérdidas aguas arriba de la subestación.
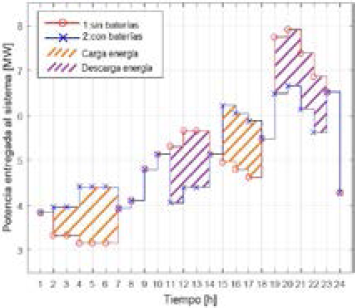
En la Figura 5 se muestran las curvas de carga con la energía que entrega la red, para ambos casos de estudio. El factor de carga para los casos 1 y 2 es 0,63 y 0,75 respectivamente, lo cual indica un aplanamiento de la curva de carga por a la presencia de los almacenadores de energía. En esta misma figura se muestra que la potencia máxima en la hora 20 pasa de 7,91 mw (caso 1) a 6,65 mw (caso 2), con una disminución de 1,26 mw. El incremento de este valor respecto al modelo anterior es 8 kW, lo cual se debe al valor considerado de las pérdidas de la red.
En la Figura 6 se describen los costos anualizados de la inversión inicial, así como el costo de mantenimiento y operación. También se presenta la ganancia por compra y venta de energía, con lo que se obtiene un valor anual de USD 36.994,1.
Sistema de prueba 2
Este sistema tiene 34 nodos y se ilustra en la Figura 7, la cual evidencia que la fuente está conectada en el nodo 1 y el sistema de almacenadores de energía, en el nodo 2 (subestación). Los nodos 3-34 tienen demandas asociadas y la línea entre los nodos 1-2 representa el equivalente de Thévenin de la red conectada aguas arriba del nodo 2 (subestación). En este sistema el costo de los almacenadores de energía es de USD 150.000 y su costo anual de operación y mantenimiento, de USD 6.250.
Modelo lineal
Al solucionar este modelo se obtienen los resultados de la Tabla 1; en esta se observa que la situación más económica es aquella en la cual se usan almacenadores de energía (caso 2), con una utilidad diaria de USD 143,25 (USD 52.286,25 anuales). Las curvas de carga de ambos casos se ilustran en la Figura 8, donde las líneas con círculos pequeños y líneas con x corresponden a los casos 1 y 2, respectivamente.
Tabla 3. Resultados del sistema de prueba 2, modelo lineal (USD)
|
Caso |
Función objetivo |
|---|---|
|
1 |
5.849,70 |
|
2 |
5.706,45 |
Fuente: elaboración propia.
De la Figura 8 se obtiene un factor de carga de 0,64 para el caso 1 y 0,74 para el caso 2; esto refleja una mejor distribución de la curva de carga del sistema, y se obtiene así una curva de carga más aplanada.
Respecto a la demanda máxima presentada en la hora 20, se aprecia que pasa de 3,71 en el caso 1 a 2,96 mw en el caso 2; así, se consigue una disminución de 0,75 mw. Esta reducción representa una mejora en la cargabilidad de los elementos del sistema y, por ende, un mejoramiento de las pérdidas de energía eléctrica de la red.
En la Figura 9 se muestra un diagrama de flujo con los costos anualizados, que incluye el costo del equipo, su mantenimiento y operación, así como la ganancia por compra y venta de energía. Con base en lo anterior, el costo anualizado del almacenador es de USD 24.411,8. En esta figura se aprecia que la ganancia anual (diferencia entre utilidad y costo de inversión, operación y mantenimiento) es de USD 21.624,5.
Modelo no lineal
Para incluir en el modelo matemático el efecto de las pérdidas de energía aguas arriba de la subestación, se usa el equivalente de Thévenin. Así, es comprendido en el análisis de forma aproximada el efecto de las pérdidas de energía durante las horas del día, así como el valor de las pérdidas en la hora pico. En la Tabla 4 se presentan los resultados de la función objetivo del modelo no lineal, para ambos casos de estudio.
Tabla 4. Resultados del sistema de prueba 2, modelo no lineal (USD)
|
Caso |
Función objetivo |
|---|---|
|
1 |
6.184,39 |
|
2 |
6.040,01 |
Fuente: elaboración propia.
De la Tabla 4 se puede concluir que los valores obtenidos con el modelo no lineal son mayores que los obtenidos con el modelo lineal, debido al efecto de las pérdidas. También se observa que el caso más económico es el que usa almacenadores de energía (caso 2), con una utilidad diaria de USD 144,38 (USD 52.698,7 anuales). Este valor es mayor al del modelo lineal por el efecto de las pérdidas aguas arriba de la subestación.
En la Figura 10 se muestran las curvas de carga con la energía que entrega la red, para ambos casos de estudio. El factor de carga para los casos 1 y 2 es 0,64 y 0,77, respectivamente, lo cual indica un aplanamiento de la curva de carga por causa de la presencia de los almacenadores de energía. En esta misma figura se observa que la potencia máxima en la hora 20 pasa de 3,89 mw (caso 1) a 3,14 mw (caso 2), con una disminución de 0,75 mw. El incremento de este valor respecto al modelo lineal es 2 kW, lo cual se debe al valor considerado de las pérdidas de la red.
En la Figura 11 se presenta un diagrama de flujo con los costos anualizados, que incluye el costo del equipo, su mantenimiento y operación, así como la ganancia por compra y venta de energía. En esta figura se aprecia que la ganancia anual (diferencia entre utilidad y costo de inversión, operación y mantenimiento) es de USD 22.036,9.
Comentarios finales
Para trabajos futuros se puede considerar la localización óptima de sistemas de almacenamiento de energía en sistemas de distribución utilizando el modelo no lineal, que permite representar las pérdidas de energía. Este nuevo modelo sería un problema de programación no lineal entera mixta (PNLEM), que podría ser resuelto mediante el uso de una metaheurística, utilizando como flujo de carga el modelo no lineal planteado en este artículo. También es posible incluir generación distribuida en este problema, agregando las restricciones generadas por cada generador, dependiendo de su tecnología; de esta forma, surge un problema más general que tiene en cuenta almacenadores de energía y energías renovables. Además, se puede adicionar esta metodología con la propuesta de [17], para considerar el planeamiento integrado de sistemas dedistribución con almacenadores de energía, el cual podría ser resuelto mediante el uso de una metaheurística, utilizando como flujo de carga el modelo no lineal o lineal planteado en este artículo.
El análisis de la ubicación de almacenadores de energía en transmisión debido al impacto de los almacenadores ubicados en distribución también puede ser estudiado a partir de un equivalente de Thévenin para transmisión y generando una metodología bi-nivel. Este sería un problema interesante dado que en transmisión se busca mejorar solo los picos de alta demanda, mientras que en distribución se ve desde la perspectiva de compra y venta de energía eléctrica y puede que estos dos objetivos se encuentren en conflicto.
Conclusiones
Se propone una metodología para resolver el problema de la operación en sistemas de distribución con almacenadores de energía. El modelo matemático planteado considera como función objetivo la compra de energía y las pérdidas de energía en la red, y está sujeto a restricciones técnicas y operativas de la red y los almacenadores. Son propuestos, entonces, un modelo lineal y uno no lineal; el primeroconsidera la compra de energía, y el segundo, además de lo anterior, las pérdidas técnicas del sistema. Los modelos son analizados con dos casos de prueba y resueltos con el software de optimización comercial gams.
A pesar de que con los dos modelos se obtienen soluciones relativamente semejantes, el modelo no lineal presenta resultados más próximos a los de la operación real de las redes eléctricas, ya que tiene encuenta para su análisis el efecto de las pérdidas. Las pérdidas de la red de transmisión son representadas a través de un equivalente de Thévenin localizado en la subestación. El modelo lineal es de fácil implementación y bajo requerimiento de cómputo, por lo que también resulta atractiva su implementación.
La instalación de almacenadores de energía es un negocio viable para los operadores de red y representa una alta rentabilidad. El tiempo de repago del equipo almacenador es bajo. Anualmente son obtenidas altas ganancias, como consecuencia de la compra y venta de energía; además, se logra una mejora en el nivel de pérdidas de energía eléctrica y de confiabilidad en la red de transmisión.