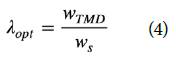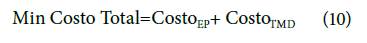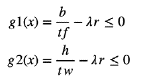Introducción
Con el objetivo de mejorar la respuesta de una estructura ante un evento sísmico de magnitud considerable, la academia y la industria han hecho un esfuerzo conjunto para desarrollar y utilizar un importante número de sistemas de protección sísmica (SPS). Mientras que estructuras convencionales disipan la energía del sismo por medio de deformaciones permanentes en los elementos estructurales, estructuras con SPS cuentan con dispositivos que absorben o disipan gran parte de la energía del sismo y evitan mayores niveles de daño a la estructura principal. En ese sentido, tal tipo de solución es atractiva para el diseño de edificaciones en zonas de amenaza sísmica alta, como es el caso de Colombia. Sin embargo, aún son pocas las edificaciones en el país que cuentan con tal tecnología. Una de las razones para ello está asociada con el costo inicial del sistema estructural resultante.
Un amortiguador de masa sintonizada TMD (Tuned Mass Damper) es un dispositivo que entra en la categoría de SPS de tipo inercial. Este se compone de una masa y de un elemento que proporciona rigidez y amortiguamiento [1]. El principio de funcionamiento del TMD se basa en conseguir que la masa oscile como un péndulo alrededor de la posición de equilibrio durante el movimiento sísmico. De tal forma que se generen fuerzas que contrarresten los movimientos del sistema principal. Es importante anotar que existen diversos factores que impactan el desempeño de un TMD en su tarea de reducir la respuesta sísmica de una estructura. Young-Rak et al. [2] demostraron que la eficiencia de un conjunto de TMDS para controlar la respuesta sísmica es afectada por la posición de los dispositivos en la estructura. Espinoza et al. [3] desarrollaron una metodología que consideraba la influencia del contenido frecuencial de la señal sísmica sobre la definición de los parámetros de sintonización de un TMD. Barros et al. [4] encontraron que la eficiencia de un TMD de bastante peso depende sobre la ductilidad y rigidez del sistema principal. Nakai et al. [5] desarrollaron un TMD de gran tamaño que permitió contrarrestar los efectos de terremotos de períodos largos en edificios de gran altura mediante una modificación de su coeficiente de amortiguamiento.
En lo relacionado a la definición de las propiedades del TMD (masa, rigidez y amortiguamiento), Chang en 1990 [6] estableció, inicialmente, un conjunto de ecuaciones sencillas que relacionan las propiedades óptimas del TMD a aquellas de la estructura. Este estudio ha sido utilizado como base de muchas investigaciones reportadas en la literatura. Kaveh et al. [7] utilizaron un algoritmo de optimización caótico para determinar la rigidez y amortiguamiento óptimo de un TMD. Lo anterior, considerando como criterio de diseño una función objetivo que combina desplazamientos y aceleraciones. Khazaei et al. [8] estudiaron el efecto de la localización en altura de múltiples TMDS para disminuir la respuesta sísmica en edificios de acero altos con plantas en forma de U y L. Caicedo et al. [9] propusieron un algoritmo de evolución diferencial para la optimización de las propiedades de TMDS en edificios de gran altura. Para ello, consideraron diferentes funciones objetivo basadas en desplazamientos y aceleraciones de piso. Soheili et al. [10] desarrollaron una metodología para la determinación óptima de los parámetros de un TMD que utiliza un algoritmo de colonia de hormigas, una función objetivo basada en la máxima deriva para la reducción y consideraciones de la interacción suelo-estructura.
Como se puede observar, los trabajos anteriores están orientados a optimizar los parámetros y/o localización de los TMDS. Pero no se explora la posibilidad de estudiar el sistema estructura principal-TMD como una única estructura. En este trabajo se propone una metodología para la optimización de edificios aporticados de acero en Colombia, equipados con un amortiguador de masa sintonizada (TMD en el último piso como parte de su sistema de resistencia sísmica). El problema de optimización es resuelto mediante una técnica heurística, ya que estas han mostrado buen desempeño en la solución de problemas del área de ingeniería estructural. La función objetivo corresponde al costo total de la estructura (elementos estructurales más TMD).
1. Amortiguadores de masa sintonizada
De forma ideal, un amortiguador de masa sintonizada (TMD) está constituido por un elemento de masa que se conecta a la estructura principal a través de un elemento tipo resorte y otro tipo amortiguador viscoso como se observa en la figura 1a. Actualmente, estos dispositivos son producidos a nivel industrial como aquel presentado en la figura 1b de la empresa Maurer.

Fuente: www.maurer.eu
Figura 1 Amortiguadores de masa sintonizada: a) representación, b) ejemplo real de la empresa Maurer.
La disipación de la energía del sismo se alcanza cuando el movimiento del TMD entra en desfase con aquel de la estructura principal. Lo cual se alcanza mediante la sintonización de las frecuencias del dispositivo y de la edificación. En ese sentido, la ecuación de movimiento que describe el comportamiento en dos direcciones del piso superior de una estructura con TMD ante una carga sísmica viene dada por [11]:
donde m, c y k son las propiedades del amortiguador (masa, amortiguamiento y rigidez, respectivamente) que deben definirse en las direcciones x e y. La acción sísmica es definida en término de las aceleraciones
 y
y
 del terreno y en las direcciones x e y, respectivamente. Mientras que la respuesta del último piso es medida en término de las aceleraciones relativas al terreno y en las direcciones x e y, respectivamente. Es importante anotar que esta formulación considera que el comportamiento de la estructura principal es elástico durante el sismo.
del terreno y en las direcciones x e y, respectivamente. Mientras que la respuesta del último piso es medida en término de las aceleraciones relativas al terreno y en las direcciones x e y, respectivamente. Es importante anotar que esta formulación considera que el comportamiento de la estructura principal es elástico durante el sismo.
La determinación de las propiedades del TMD (masa, rigidez y amortiguamiento) para una estructura específica ha sido objeto de estudio desde hace varias décadas. Chang [6] propuso que el diseño del TMD esté basado en la relación (μ) de las masas del TMD (mTMD) y del sistema principal (ms):
la cual está comúnmente entre el 1% y 3%. A partir de este valor se obliga a que la relación (λ opt ) entre la frecuencia natural del TMD (wTMD) y la frecuencia del modo fundamental del sistema principal (ws) sea cercana a 1, así:
A partir de esta información se puede determinar la rigidez del TMD mediante:
Por último, se calcula el amortiguamiento óptimo según la expresión deducida en [6]:
2. Algoritmo de evolución diferencial
El algoritmo de evolución diferencial (DEA) es una heurística de búsqueda estocástica basada en población. Fue desarrollado por Rainer y Kenneth en 1995 para resolver problemas de optimización global con espacios de búsqueda grandes y complejos [12]. Su formulación matemática se fundamenta en la teoría de la evolución natural. En esta, una población de individuos (representaciones de soluciones del problema) se somete iterativamente a la aplicación de operadores genéticos para alcanzar la evolución (generación de nuevas soluciones de alta calidad). Cada individuo de la población se forma por un vector que representa una posible solución al problema analizado (cada componente del vector representa a una de las variables del problema) y por su correspondiente valor de calidad (costo). La generación de la población inicial, de tamaño NV, se puede realizar de forma aleatoria o mediante heurísticas basadas en el conocimiento del problema.
El primer operador que se aplica sobre la población se conoce como mutación. Tiene como objetivo la generación de individuos desde la población actual dado que el cruce de estos puede llevar a mejores individuos. Existen muchos operadores de mutación reportados en la literatura, siendo uno comúnmente utilizado [12]:
Donde V i,g = Vector mutado, F = Factor de mutación, X ri , g = Vectores aleatorios de la población inicial y X best,g = Vector con mayor costo en la población en la generación g. El valor del factor de mutación definido por el usuario afecta la calidad de la solución y la velocidad de convergencia.
Con el fin de incrementar la diversidad del espacio de búsqueda, se procede al proceso de cruce donde se combinan parámetros del vector inicial con el vector mutante para obtener un vector de prueba dado por [12]:
donde CR es la tasa de cruce e indica qué porcentaje del vector mutante y del vector objetivo (x i,g,j ) formará parte del vector de prueba. El rango para CR es de 0 a 1.
Por último, se realiza el proceso de selección en el cual el vector de prueba y el vector objetivo se evalúan en la función objetivo, y el que tenga una mejor solución o aptitud pasará a la siguiente generación.
Este proceso se repite en sucesivas generaciones hasta que se alcance un criterio de paro. Por ejemplo, un número máximo de generaciones, NMG.
3. Metodología propuesta
A continuación, se propone una primera aproximación para la obtención de un diseño de pórticos regulares de acero equipados con TMDS.
Esto mediante un proceso de optimización cuyas variables de diseño involucran tanto la estructura principal como el dispositivo de protección sísmica y la consideración del costo total de la estructura. Dado el alcance de la investigación, la metodología propuesta utiliza algunas simplificaciones del problema en su formulación:
■ La función de costo es simplificada a materiales, como es comúnmente adoptado en la literatura.
■ El TMD no proviene de una empresa comercial siendo que su costo está asociado con materiales que se pueden conseguir en el país. Así, este permite tener una estimación de materiales de un producto construido localmente.
■ Las estructuras analizadas no presentan irregularidades en planta y altura.
■ Dado que no existe en Colombia un reglamento para estructuras con TMDS, se asume que el dimensionamiento de los elementos del pórtico será realizado siguiendo las directrices del Reglamento Colombiano de Construcciones Sismo Resistentes (NSR-10) [13], con la consideración de que la estructura principal permanecerá en el régimen elástico. Esto permite la realización de un análisis dinámico lineal para la consideración de la amenaza sísmica sobre la edificación.
■ En este trabajo se asume que la amenaza está formada por 3 registros sísmicos escalados por amplitud y se toma la respuesta máxima de la estructura para efectos de diseño. La utilización de solamente 3 registros ayuda a disminuir el costo computacional asociado con el análisis dinámico de cada solución estructural. Se asume que los registros seleccionados son compatibles con la amenaza del lugar de construcción.
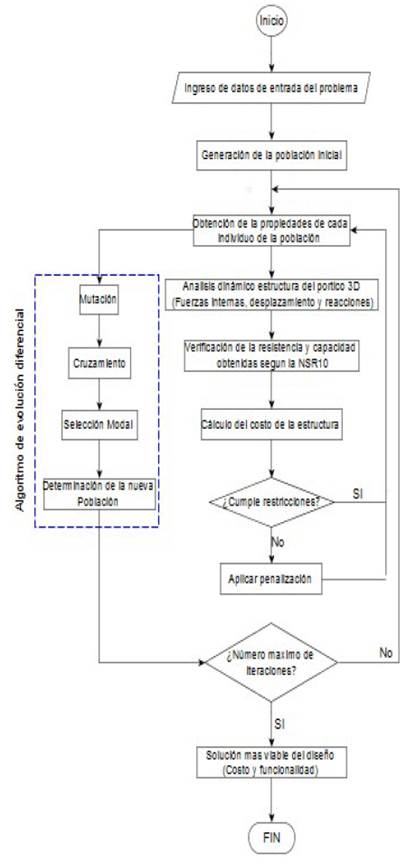
La figura 2 muestra la metodología propuesta y posteriormente se describen los detalles específicos de cada paso, incluyendo las suposiciones realizadas.
En primera instancia, el algoritmo requiere que el usuario suministre tanto las características de la edificación (dimensiones, cargas, base de datos de perfiles, rango de valores del TMD, sismos de análisis) como los parámetros del DEA (CR, F, NV, NMG). A partir de esta información, se inicializa la primera población de soluciones que consiste de NV pórticos regulares de acero equipadas con TMDS. Estos presentan configuraciones estructurales (perfiles y propiedades del TMD) diferentes. Para cada estructura se debe determinar la respuesta sísmica máxima (desplazamientos, derivas, fuerzas internas). Para el conjunto de sismos definidos por la amenaza mediante un análisis dinámico cronológico lineal, se adoptan 3 registros. Seguidamente, se evalúan las restricciones de comportamientos locales (elementos) y globales (estructura) y se calcula el costo de cada configuración estructural. Si una configuración estructural no cumple con al menos una restricción, se procede a penalizar el costo de dicha configuración con el objetivo de que pueda ser descartada por el proceso de optimización.
Al finalizar todas las estructuras en la población actual, la solución de menor costo en la población corresponderá a la mejor solución para la generación actual. Una nueva población es generada mediante las operaciones del algoritmo DEA establecidas en la sección 2 junto con las modificaciones presentadas en la sección 4.2. Se predefine un número máximo de iteraciones como criterio de paro en la base de pruebas preliminares sobre la cantidad que permite garantizar la convergencia. La solución final del algoritmo DEA debe ser el resultado de ejecutarlo en un número determinado de veces dada su naturaleza estocástica. Debe verificarse que la solución óptima satisfaga todas las restricciones del problema.
3.1. Planteamiento del problema
3.1.1. Variables de diseño
En este problema, las variables de diseño corresponden a las secciones de los elementos estructurales (vigas y columnas) para cada piso de la edificación. Además de la relación de masa entre el TMD y el sistema principal. En el caso de los elementos estructurales, se debe escoger el perfil estructural de acero de cada piso desde una base de datos de perfiles disponibles. En ese sentido, la variable corresponde a la posición del perfil dentro de una base de datos, la cual está organizada en función de la inercia de cada perfil e incluye perfiles que van desde el W4x13 al W 44x335. A pesar de que son 3 los parámetros del TMD, mediante la definición de la relación de masas (se permite un rango de valores entre 0.005 y 0.01) se puede determinar la rigidez y el amortiguamiento mediante las Ecs. 5 y 6, respectivamente.
3.1.2. Función objetivo
La función objetivo que define la optimización del diseño de estructuras está comúnmente asociada con la minimización del costo de la configuración estructural obtenida. En este caso, tenemos un costo asociado a la estructura principal (COS-TOEP) y un costo asociado al TMD (COSTOTMD), así:
En este trabajo, se hace la suposición que los costos estarán asociados únicamente a los materiales de vigas, columnas y del TMD. Existen otros costos derivados, por ejemplo, de la parte constructiva o las conexiones. Sin embargo, una función de costo detallada será objeto de mayor estudio en una investigación posterior. Así las expresiones de costo quedan:
dónde Ca es el costo del acero por metro lineal, L es la longitud del elemento (m), NV es el número de vigas, NC es el número de Columnas, Psvi es el peso de la sección de la viga (kg/m), Psci es el peso de la sección de la columna (kg/m). Para efectos de este trabajo, se considera que el TMD corresponde a un bloque de concreto que se conecta mediante aisladores elastoméricos a la estructura principal. Así que Volc es el volumen del bloque de concreto (m3), Ce es el esto del concreto por m3, Cc es el costo del acero por kg, y Cne es el esto del neopreno por volumen. No se incluyen otros estos como formaletas para la fundición del concreto.
3.1.3. Restricciones
Las restricciones para el problema en estudio vienen desde aspectos funcionales y constructivos. La estructura principal debe ser diseñada para cumplir con los requisitos dados en el capítulo F del Reglamento Colombiano de Construcción Sismo Resistente NSR-10 [13]. En este caso, se supone que la estructura se encuentra ubicada en una zona de amenaza sísmica intermedia. Razón por la cual se consideran los lineamientos del reglamento para estructuras con capacidad moderada de disipación de energía DMU. Sin embargo, es importante anotar que se considerará que la estructura principal permanece en el rango elástico para la amenaza del lugar. La tabla 1 muestra todas las restricciones definidas para el problema, donde b: aneho de aleta, tf: espesor Aleta, h: altura de alma, tw: espesor de alma, k: rigidez, L: longitud efectiva, r: radio de giro, Δ permisible= L/360 Pu = resistencia de compresión axial requerida, Pn = resistencia de compresión axial disponible. Mu = resistencia de flexión requerida, Mn = resistencia de flexión disponible en la dirección de análisis. (X eje fuerte. Y eje débil) Φ = factor de resistencia. 0.90. Δ i max:. deriva máxima, "h pi : altura de piso. sci= sección de la columna del piso. Sei-1= sección de la columna del piso inferior.
Tabla 1 Restricciones del problema de optimización.
| Concepto | Restricción * | Ecuación |
|---|---|---|
| Chequeo de esbeltez de la sección para elementos a compresión: aleta y alma | (13,14) | |
| Chequeo de ductilidad de los elementos: aletas y alma | (15, 16) | |
| Chequeo de esbeltez en longitud para elementos a compresión. | (17, 18) | |
| Chequeo de compacta/no compacta de la sección para elementos a flexión | (19, 20) | |
| Deflexiones en vigas | (21, 22) | |
| Límite de resistencia de los elementos a flexión | (23, 24) | |
| Límite de resistencia de los elementos a flexocompresión | (25) | |
| Derivas edificio | (26) | |
| Restricciones de geometría | (27) |
Fuente: elaboración propia.
3.2. Configuración del algoritmo de evolución diferencial
En este trabajo se utiliza el algoritmo DEA presentado en la sección 2 como método de optimización. Sin embargo, esta versión fue modificada para mejorar su desempeño respecto al problema en estudio. Ya que es posible que el espacio de búsqueda del problema sea multimodal. Con lo cual, diferentes configuraciones estructurales pueden producir valores similares de la función objetivo. Para ello, se utiliza la propuesta dada en la referencia [14] para tratar con múltiples óptimos locales. Esta está basada en el cálculo de la distancia euclidiana entre individuos para definir la presencia de óptimos locales y, con ello, generar mayor exploración del espacio de búsqueda.
Asimismo, se pretende que el usuario no tenga que definir los parámetros F y CR del DEA cuando vaya a utilizar la metodología. En ese sentido, se emplea la estrategia definida en [15] que consiste en permitir que cada vector de la población tenga sus propios parámetros en cada generación del proceso de búsqueda. Como dado por:
donde Τ1 y T2 tiene un valor de 0.1, Fu=0.9 y F1=0.1. Los valores de CR varían entre [0,1]. Rand1 y rand2 son valores aleatorios entre 0 y 1 que siguen una distribución uniforme. El tamaño de la población debe ser definido por el usuario mediante prueba y error. Dado que depende de la complejidad del problema.
4. Ejemplos numéricos
4.1. Casos de estudio
Para mostrar el desempeño de la metodología propuesta, se presentan los resultados correspondientes a la optimización de cuatro edificaciones en estructura metálica, regulares, compuestas de una luz de 3.00 m en ambos sentidos (X y Y), de 5, 7, 9 y 12 pisos con una altura de entrepiso de 4.00 m (ver figura 3). El material de los perfiles presenta límite de fluencia de 345 MPa, módulo de elasticidad 200,000 MPa, resistencia a la tracción de 450 MPa, peso específico de 7850 kg/m3. Respecto al TMD, se asumieron las propiedades presentadas en el trabajo de Meza y Manrique [16]. En cuanto a las cargas utilizadas, se consideró el peso propio de los elementos estructurales, la placa de entrepiso con un espesor de 0.20 m y la fuerza sísmica. Para la fuerza sísmica se tomaron los acelerogramas de los sismos de Lomaprieta (sismo 1), Coalinga (sismo 2) y El Centro (sismo 3) escalados a una aceleración de 0.35g. Estos sismos se asumen como representativos de la amenaza en el lugar de construcción. Siendo que debe ser definida la amenaza para el sitio de construcción.
Los costos de los materiales, tanto del acero como del concreto, se determinaron a partir de la base de datos dada en la revista Construdata. Mientras que, para el costo del TMD, se tomó como referencia lo reportado por Meza y Manrique [16]. Es importante anotar que en la medida en que los costos cambien, se obtendrán soluciones que pueden ser diferentes, pero la concepción de la metodología como tal no se modifica. Respecto al algoritmo de optimización, se hacen 5 ejecuciones dada la naturaleza estocástica del algoritmo de optimización. Siendo reportada como solución la ejecución con la estructura que reporta el menor costo. El tamaño de la población de vectores para cada uno de los ejemplos se tomó como 30 después de un proceso de prueba y error.
4.2. Estructuras optimizadas
Las tablas 2 a 5 presentan la solución encontrada mediante la metodología propuesta para cada una de las edificaciones analizadas. En dichas tablas, se reporta la configuración de perfiles y la relación de masa del TMD obtenidas para cada uno de los sismos analizados. Así como el diseño final de la estructura a aquella configuración estructuralmente más robusta. Adicionalmente, se hace la optimización del pórtico sin TMD para efectos de comparación con la solución estructural, incluyendo la protección sísmica. Considerando un R=7 para el diseño de esta estructura. Puede observarse que en función del sismo utilizado las configuraciones estructurales obtenidas pueden variar significativamente, produciendo diferencias en costos mayores al 50%.
Tabla 2 Resultado: edifìcio de 5 pisos
| Variables | Descripción | Sismo 1 | Sismo 2 | Sismo 3 | Resultado Final | Sin TMD |
|---|---|---|---|---|---|---|
| V1 | Viga | W10X30 | W8X15 | W8X48 | W8X48 | W6X16 |
| V2 | Columna 5-4 piso | W10X30 | W10X112 | W8X48 | W8X48 | W21X132 |
| V3 | Columna 4-3 piso | W12X50 | W10X112 | W8X48 | W8X48 | W21X132 |
| V4 | Columna 3-2 piso | W14X74 | W10X112 | W8X48 | W8X48 | W21X147 |
| V5 | Columna 2-1 piso | W21X93 | W10X112 | W27X236 | W27X236 | W27X258 |
| V6 | Columna 1-0 piso | W14X193 | W21X132 | W18X311 | W18X311 | W33X263 |
| V7 | Relación de masa | 0.90% | 2.80% | 2.00% | 2.00% | - |
| Costo | $105,386,513 | $132,910,195 | $183,307,317 | $183,307,317 | $177,449,250 | |
| 13 | 95 | 17 | 17 | 50 |
Fuente: elaboración propia.
Tabla 3 Resultado: edifìcio de 7 pisos
| Variables | Descripción | Sismo 1 | Sismo 2 | Sismo 3 | Resultado Final | Sin TMD |
|---|---|---|---|---|---|---|
| V1 | Viga | W14X132 | W16X89 | W16X77 | W16X77 | W21X122 |
| V2 | Columna 7-6 piso | W24X207 | W18X158 | W14X233 | W14X233 | W21X122 |
| V3 | Columna 6-5 piso | W24X207 | W36X330 | W27X336 | W27X336 | W21X122 |
| V4 | Columna 5-4 piso | W24X207 | W36X330 | W27X336 | W27X336 | W21X122 |
| V5 | Columna 4-3 piso | W30X292 | W36X330 | W27X336 | W27X336 | W21X122 |
| V6 | Columna 3-2 piso | W30X292 | W36X330 | W14X455 | W14X455 | W12X305 |
| V7 | Columna 2-1 piso | W14X398 | W24X370 | W14X455 | W14X455 | W24X306 |
| V8 | Columna 1-0 piso | W14X398 | W24X370 | W14X455 | W14X455 | W24X306 |
| V9 | Relación de masa | 3.00% | 2.00% | 2.20% | 2.20% | - |
| Costo | $292,632,0 | $395,794,4 | $492,742,9 | $492,742,9 | $365,684,4 | |
| 12 | 75 | 19 | 19 | 00 |
Fuente: elaboración propia.
Tabla 4 Resultado edifìcio 9 pisos
| Variables | Descripción | Sismo 1 | Sismo 2 | Sismo 3 | Resultado Final | Sin TMD |
|---|---|---|---|---|---|---|
| V1 | Viga | W8X58 | W6x16 | W10x30 | W10x30 | W8x15 |
| V2 | Columna 9-8 piso | W8X58 | W6x16 | W18x258 | W18x258 | W8x15 |
| V3 | Columna 8-7 piso | W21X83 | W24x162 | W18x258 | W18x258 | W21X147 |
| V4 | Columna 7-6 piso | W24X131 | W24x162 | W33x318 | W33x318 | W21X147 |
| V5 | Columna 6-5 piso | W24X131 | W12x252 | W33x318 | W33x318 | W21X147 |
| V6 | Columna 5-4 piso | W24X131 | W24x279 | W33x318 | W33x318 | W14x176 |
| V7 | Columna 4-3 piso | W14x176 | W33x354 | W33x318 | W33x318 | W12x336 |
| V8 | Columna 3-2 piso | W14x176 | W36x361 | W33x318 | W33x318 | W36x395 |
| V9 | Columna 2-1 piso | W27x217 | W36x361 | W33x318 | W33x318 | W36x395 |
| V10 | Columna 1-0 piso | W14x311 | W36x361 | W14X550 | W14X550 | W36x395 |
| V11 | Relación de masa | 1.50% | 1.00% | 1.10% | 1.10% | - |
| Costo | $332,112,493 | $418,301,016 | $661,244,425 | $661,244,425 | $402,577,830 | |
| 93 | 16 | 25 | 25 | 30 |
Fuente: elaboración propia.
Tabla 5 Resultado edifìcio 12 pisos
| Variables | Descripción | Sismo 1 | Sismo 2 | Sismo 3 | Resultado Final | Sin TMD |
|---|---|---|---|---|---|---|
| V1 | Viga | W8X21 | W8X21 | W8X15 | W8X15 | W10X30 |
| V2 | Columna 12-11 piso | W8X21 | W21X48 | W8X15 | W8X15 | W10X30 |
| V3 | Columna 11-10 piso | W10X112 | W21X166 | W17X77 | W17X77 | W10X45 |
| V4 | Columna 10-9 piso | W10X112 | W21X166 | W18X211 | W18X211 | W21X166 |
| V5 | Columna 9-8 piso | W18X130 | W21X166 | W40X294 | W40X294 | W21X166 |
| V6 | Columna 8-7 piso | W24X250 | W21X166 | W24X306 | W24X306 | W21X166 |
| V7 | Columna 7-6 piso | W33X291 | W24X176 | W30X326 | W30X326 | W21X166 |
| V8 | Columna 6-5 piso | W33X291 | W24X176 | W30X326 | W30X326 | W18X283 |
| V9 | Columna 5-4 piso | W12X305 | W27X217 | W30X326 | W30X326 | W18X283 |
| V10 | Columna 4-3 piso | W33X318 | W27X217 | W30X326 | W30X326 | W24X306 |
| V11 | Columna 3-2 piso | W33X318 | W40X264 | W24X335 | W24X335 | W24X306 |
| V12 | Columna 2-1 piso | W30X326 | W12X279 | W24X335 | W24X335 | W14X342 |
| V13 | Columna 1-0 piso | W36X361 | W40X327 | W24X335 | W24X335 | W40X392 |
| V14 | Relación de masa | 1.50% | 1.00% | 1.10% | 1.10% | - |
| Costo | $422,958,054 | $466,981,905 | $483,237,878 | $483,237,878 | $502,914,960 | |
| 54 | 05 | 78 | 78 | 60 |
Fuente: elaboración propia.
En el caso del pórtico de 9 pisos, se observó que es muy susceptible al sismo 3. Dando como resultado una estructura muy robusta. Esta solución podría indicar también que el algoritmo quedó atrapado en un óptimo local. Cabe mencionar que la respuesta obtenida por el algoritmo se puede mejorar si se aumenta el número de ejecuciones y el número de registros sísmicos utilizados a por lo menos 7 de tal forma a utilizar el promedio de la solución. No obstante, lo anterior implica un aumento del costo computacional. Por lo que se deben definir estrategias para manejar este aspecto.
Igualmente, la relación óptima de la masa del TMD no presenta un valor similar independiente de la estructura. Lo cual indica que para diseñar una estructura con TMD en particular, se debe hacer por lo mínimo un proceso iterativo donde se varía tal relación. Respecto a la solución sin TMD, se observa un incremento del costo inicial en la mayoría de los casos. Siendo que para la estructura de 12 pisos no se cumplió con la restricción de derivas máximas, tornando esa solución inviable. Es importante resaltar que el desempeño sísmico de la estructura con TMD sería mejor que el que presenta su correspondiente sin TMD. Teniendo en cuenta los perfiles y la relación de masa obtenida por medio de la metodología de optimización, en la figura 4 se muestran los desplazamientos máximos generados en edificio de 7 pisos, con la configuración establecida. Así, se puede observar cómo los desplazamientos disminuyen significativamente en un 38% cuando se acopla el TMD a la estructura con una relación de masa de 2.2 %. Obteniendo unos desplazamientos máximos sin TMD de 0.058 m y con TMD de 0.024 m.

Fuente: elaboración propia.
Figura 4 Desplazamientos máximos estructura de 7 pisos con y sin TMD con una relación de masa del 2.1% para el sismo de Lomaprieta.
En la tabla 6, se muestran los resultados de la relación demanda-capacidad de cada uno de los elementos estructurales (vigas y columnas) y derivas máximas que se obtienen con los perfiles generados en el proceso de optimización para la estructura de 7 pisos con TMD y sin TMD. La intención es corroborar que cumple con las solicitudes impuestas. Como se puede analizar, los perfiles obtenidos para la estructura sin TMD son menores a los de la estructura con TMD. Lo anterior, se debe a que en el proceso de optimización el algoritmo no encuentra una solución viable que satisficiera las restricciones. En este caso la deriva máxima no cumple con la admisible. Por el contrario, la estructura con TMD cumple con todas las restricciones en cuanto a capacidad y desplazamientos permisibles de la estructura. Por lo cual es la solución viable para el problema.
Tabla 6. Verificación resultados edifìcio de 7 pisos
| Estructura | 7 pisos con TMD | 7 pisos sin TMD |
|---|---|---|
| Viga | 0.032 | 0.05 |
| D/C columnas 7-6 piso | 0.0563 | 0.071 |
| D/C columnas 6-5 piso | 0.0577 | 0.21 |
| D/C columnas 5-4 piso | 0.1277 | 0.28 |
| D/C columnas 4-3 piso | 0.1365 | 0.26 |
| D/C columnas 3-2 piso | 0.1376 | 0.28 |
| D/C columnas 2-1 piso | 0.299 | 0.26 |
| D/C columnas 1-0 piso | 0.299 | 0.26 |
| Deriva máxima (m) | 0.024 | 0.052 |
| Deriva admisible (m) | 0.40 | 0.40 |
Fuente: elaboración propia.
4.3. Análisis de convergencia
En las figuras 5 y 6 se muestra el proceso de convergencia para 5 ejecuciones de la estructura de 7 y 12 pisos con el sismo del Lomaprieta. Se destacan los aspectos a continuación:
◾ El punto de inicio de cada una de las curvas no es el mismo, debido a que una población inicial de soluciones se genera de forma aleatoria. Con lo cual puede haber presencia de mejores soluciones en una ejecución determinada.
◾ En todos los casos se observa que la solución mejora con el proceso de optimización, llegando a obtener en todas las ejecuciones soluciones que satisfacen todas las restricciones.
◾ En algunos tramos de las distintas gráficas de convergencia se presentan períodos prolongados de generaciones, donde el algoritmo se queda atrapado sin generar una mejor solución. Se deben introducir mejoras en el algoritmo que permitan hacer refinamientos locales de la mejor solución, mientras se avanza en el proceso de optimización.
4.4. Análisis de robustez del algoritmo
Tomando los valores de 10 ejecuciones para el edificio de 7 y 9 pisos, corridos con el sismo del El Centro, se sacó la media y la desviación estándar. En la tabla 7 se muestran los resultados. Se puede observar que la desviación estándar que hay entre todas las ejecuciones es de una magnitud baja en comparación con los costos de toda la estructura. Ello hace al algoritmo que converja de buena forma y su robustez sea buena. Sin embargo, en el peor caso, se tiene una diferencia de más de 100 millones de pesos entre el costo de la mejor y peor ejecución. Lo cual muestra la importancia de que se realicen diversas ejecuciones del algoritmo. Del mismo modo, se pueden anadir otras características al algoritmo que permitan una mayor robustez.
4.5. Costo computacional
Debido al costo computacional y el número de ejemplos que se corrieron, se hicieron edificios de una luz en ambas direcciones. Ya que al aumentarle una luz más en ambos sentidos, incrementa el tiempo de corrida para el algoritmo en gran medida. Estos tiempos se aplican para una máquina Core I7 con 8GB de memoria Ram. Este aspecto aún requiere de atención con el fin de disminuir la exigencia computacional que se origina en la necesidad de realizar análisis dinámico cronológico lineal.
4.6. Efectos del tamaño de la población
La población de individuos en los problemas de optimización juega un papel importante, pues de esta dependen las mejores respuestas. Es decir que entre más individuos se creen en cada generación, hay más posibilidades de obtener una mejor respuesta. En general, existe un límite sobre el cual la mejora de la respuesta no es apreciable con un incremento de la población, pero sí hay un incremento en el costo computacional.
En las figuras 7 y 8 se muestran los resultados del proceso de optimización para las edificaciones de 7 y 9 pisos, respectivamente, cuando se varía el número de vectores de la población. En ambos casos, para poblaciones de 10 individuos se obtienen respuestas que, aparentemente, son económicas pero que no cumplen con todas las restricciones. Por lo tanto, no pueden ser consideradas como viables. Se puede considerar entonces que se puede utilizar un número de vectores de 30 para los edificios. Dado que al aumentar el número se consigue solo una reducción en el costo baja (aproximadamente 5% en el mejor de los casos). Es importante anotar que las cifras reportadas en las figuras 7 y 8 no son absolutas dada la naturaleza estocástica del problema.
5. Conclusiones
Se desarrolló una metodología, que cumple con los requisitos normativos de la NSR-10 en cuanto a capacidad, desplazamientos, ductilidad, esbeltez (sección y longitud del elemento), para la optimización del diseño de pórticos de acero resistentes a momento que incorporan amortiguadores de masa sintonizada. La característica más importante de la metodología propuesta es que simultáneamente se están optimizando los perfiles de la estructura principal y las propiedades del TMD en cuanto a la masa, rigidez y amortiguamiento. Se utilizó como herramienta de optimización al Algoritmo de Evolución Diferencial. El cual se modificó de su versión original en dos aspectos para mejorar sus características de convergencia. Se adicionaron características para la auto-adaptación de los parámetros del algoritmo. Siendo que el usuario solo debe definir el tamaño de la población debido a que depende del tamaño del espacio de búsqueda. Este parámetro presenta un valor para el cual poblaciones mayores no mejoran los resultados, así como el problema del aumento en el costo computacional. Se utilizó una característica multimodal debido a que, como se observa en los resultados, diferentes configuraciones estructurales pueden tener un costo similar.
Con respecto a las configuraciones estructurales encontradas, se observa que al aumentar la masa del TMD, se ve una mejoría en la reducción de los desplazamientos. Razón por la que este modifica el comportamiento dinámico de la estructura ante un evento sísmico. Sin embargo, si la masa aumenta en gran medida, la solución puede mejorar en cuanto a los desplazamientos, pero el costo de la edificación va a aumentar, siendo menos competitiva. Según los resultados obtenidos, se observó que las configuraciones de los perfiles obtenidos varían de acuerdo con la señal sísmica utilizada. Por ende, se recomienda realizar otras iteraciones modificando la señal sísmica.