ESTIMACIÓN DE LA DEGRADABILIDAD EFECTIVA EN EL RUMEN MEDIANTE MÉTODOS NUMÉRICOS

ESTIMATION OF EFFECTIVE DEGRADABILITY IN RUMEN TROUGH NUMERICAL METHODS

 

Héctor Jairo Correa Cardona¹

 

¹ Profesor Asociado. Universidad Nacional de Colombia, Sede Medellín. Facultad de Ciencias Agropecuarias. Departamento de Producción Animal. A.A. 1779. Medellín, Colombia. <hjcorreac@unalmed.edu.co>

 

Recibido: Junio 21 de 2008; Aceptado: Octubre 3 de 2008.

---

Resumen. La estimación correcta de la degradabilidad ruminal efectiva en el rumen (DE) de las distintas fracciones nutricionales de los alimentos es fundamental para el desarrollo de programas eficientes de alimentación para rumiantes. La propuesta clásica para estimar la degradabilidad efectiva en el rumen de la fracción potencialmente degradable (DEb=bKd/(Kd+Kp)), no es correcta  ya que se basa en la presunción de que las constantes de la cinética de la degradabilidad (Kd) y del pasaje ruminal (Kp) representan la velocidad de fermentación y de pasaje ruminal, respectivamente cuando estas realmente representan la relación constante entre la aceleración y la velocidad de degradación y de pasaje. Se presenta, entonces, una nueva propuesta coherente con las bases matemáticas de la cinética de la degradación y el pasaje ruminal de la fracción potencialmente degradable en el rumen (b) que requiere el uso de métodos numéricos para despejar el tiempo “t” de la expresión  1 = e^-kd*t + e^-kp*t, que al reemplazarlo en la expresión b*e^-kd*t, permite calcular la DEb. La estimación de la DEb por este método permite obtener datos confiables y coherentes con las bases matemáticas de la cinética de la degradación y el pasaje ruminal de las fracciones nutricionales.

Palabras claves: Degradabilidad efectiva, cinética ruminal, modelos matemáticos.

Abstract. A correct estimation of effective degradability in rumen of nutritional fractions of feedstuff is basic to develop efficient feed programs to ruminants. However, the classic proposal to estimate the effective degradability in rumen of potentially degradable fraction (EDb=bKd/(Kd+Kp)), is not correct since it is based on the presumption that the constants of the kinetics of the ruminal degradability (Kd) and passage (Kp) represent the speed of the ruminal fermentation and passage, respectively, when these really represent the constant relationship between the acceleration and speed of degradation and of passage. In this paper is then proposed a new mathematical procedure coherent with the kinematics properties of the ruminal degradation and passage of the potentially degradable fraction (b) that requires the use of numeric methods to clear the time "t" of the expression 1 = e^-kd*t + e^-kp*t, that when replacing it in the expression b*e^-kd*t, it allows to calculate EDb. The estimate of EDb for this method allows to obtain reliable and coherent data with the mathematical bases of the kinetics of the ruminal degradation and the passage of the nutritional fractions.

Key words: Effective degradability, mathematical models, rumen kinetics.

---

 

La estimación de la degradabilidad efectiva en el rumen (DE) es quizá el cálculo más importante en el estudio de la cinética ruminal dado que permite establecer la proporción de fracciones nutricionales que son degradadas y aquellas que no logran degradarse en el rumen (National Research Council, 2001). La estimación correcta de este parámetro es necesaria para un adecuado manejo nutricional de los rumiantes y, en consecuencia, para una mejor utilización de los nutrientes.

Orskov y McDonald (1979) describieron un modelo exponencial para estimar la degradabilidad ruminal de los nutrientes en función del tiempo de permanencia en el rumen con base en datos obtenidos por la técnica de degradación in situ: , donde DRb_t es la degradabilidad ruminal de la fración b en el tiempo t, a es la fracción soluble que es completamente degradable en el rumen, b es la fracción potencialmente degradable en el rumen, kd es una constante y t es el tiempo de permanencia en el rumen. Este modelo fue originalmente propuesto por Thünen (1930) para el estudio de las respuestas de los cultivos a diferentes factores de producción quien denominó a la constante kd como la tasa instantánea de decrecimiento en la productividad marginal (Humphrey, 1930). Grovum y Williams (1973), por su parte, propusieron un modelo exponencial similar para estimar el pasaje ruminal en el tiempo t (PRb_t) que incluye la estimación de la constante kp cuyas características matemáticas son similares a las de la kd.

La kd y la kp fueron incorporadas por Orskov y McDonald (1979) en una ecuación aritmética para estimar la DE de la fracción potencialmente degradable (DEb) que es correcta en el caso en el que estas constantes hagan referencia a velocidades como se demuestra en este documento. Sin embargo, Correa (2005) demostró que estas constantes no hacen referencia a la velocidad si no al cociente entre la aceleración y la velocidad, así:

,

entonces, al calcular la primera derivada, se tiene,

y al calcular la segunda derivada, se tiene,

con lo que,

Que corresponde al cociente entre la aceleración y la velocidad de degradación denominándose correctamente, como constante de la cinética de degradación ruminal (Correa, 2005).

Dado que, como se demuestra a continuación, la estimación de la DEb a partir de la ecuación propuesta por Orskov y McDonald (1979) es incorrecta, es necesario, en consecuencia, proponer un nuevo modelo para estimar este parámetro.

Es así como el objetivo de este trabajo es el de demostrar las bases matemáticas de la ecuación aritmética propuesta por Orskov y McDonald (1979) para estimar la DEb y proponer un nuevo modelo para estimar la DEb coherente con las bases matemáticas de los modelos exponenciales de Orskov y McDonald (1979) y el de Grovum y Williams (1973), para estimar la DRb_t y el pasaje ruminal (PRb_t), respectivamente, como fue descrito por Correa (2005).

La estimación clásica de la degradabilidad ruminal efectiva. Orskov y McDonald (1979) propusieron que la DE de la fracción b (DEb) podía ser estimada a partir de la expresión:

En la que tanto la kd como la kp hacen referencia, erróneamente, a las velocidades de degradación y de pasaje ruminal, respectivamente, como se demuestra a continuación.

Cuando la velocidad es constante, el espacio (s) recorrido puede calcularse como:

Si en esta expresión el espacio s es reemplazado por la DRb_t y la velocidad v es reemplazado por la kd (velocidad de degradación), la degradación ruminal de la fracción b (DRb_t) en cualquier tiempo se podría estimar como:

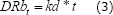
Y si la kp expresa la velocidad de pasaje, el pasaje ruminal de la fracción b (PRb_t) en cualquier tiempo se podría estimar como:

Dado que la degradación y el pasaje ruminal son las únicas fuerzas responsables de la desaparición de la fracción b en el rumen, debe existir un tiempo tal en el que la suma de la degradación y del pasaje ruminal que se presenten a ese tiempo, hallan determinado la desaparición total de la fracción b. Al despejar dicho tiempo en la expresión (3), es posible estimar la DEb. Así, al igualar la suma de las expresiones (3) y (4) a la fracción b, se tiene:

Al despejar por el factor común, la expresión (5) queda como:

Al despejar t en esta expresión, se tiene:

que al reemplazar en la expresión (3) queda la expresión (1) indicando que esta ecuación tiene validez únicamente en el caso en el que las constantes kd y kp hagan referencia a velocidades de degradación y de pasaje ruminal constantes. Dado que no es el caso de la cinética que siguen las fracciones nutricionales a su paso por el rumen (Correa 2005), es de prever que los resultados obtenidos mediante tal propuesta, sean erróneos y seguramente han sido una de las  principales causas de la ausencia de respuesta a la suplementación con fracciones nutricionales que no se degradan en el rumen (Bach et al., 1998).

Una nueva propuesta para estimar la degradabilidad ruminal efectiva. Como fue demostrado previamente (Correa, 2005), la cinética de la degradación y de pasaje de las fracciones nutricionales en el rumen es similar a la de los cuerpos que se desplazan con una aceleración variable y no a una velocidad constante. Por lo tanto, es necesario apelar a otro tipo de análisis para calcular la DEb.

La ecuación para estimar el pasaje ruminal de la  fracción b, según Grovum y Williams (1973), es:

Donde b y t ya fueron definidas y kp corresponde a la constante de la cinética de pasaje ruminal.

Ahora, y dado que como se mencionó anteriormente, las únicas fuerzas que determinan la desaparición de la fracción b desde el rumen son la degradación (DRb_t) y el pasaje ruminal (PRb_t), la suma de la desaparición de la fracción b a causa de estas dos fuerzas, es la ecuación 5:

o, lo que es lo mismo:

que resolviendo se obtiene,

Al calcular t en esta expresión y reemplazarlo en la expresión , se obtiene la DEb. Sin embargo, la ecución (10) es una expresión trascendente que no tiene solución algebraica para despejar el tiempo t. Gettys et al. (1991) afirman que a menudo resulta difícil resolver problemas cinemáticos en los que la aceleración no es constante y que solo en algunos casos especiales es posible una solución analítica. Este no es el caso de la solución para la expresión (10), lo que exige tener que apelar a procedimientos numéricos. Aunque existen muchas alternativas, es posible estimar el t en el que esta expresión se cumple mediante programas como DERIVE (Kutzler y Boykett, 1996) o la función SOLVER de Microsoft Office (Correa, 2004). Aunque es posible aplicar una solución gráfica, esta es menos precisa que la que se obtiene con el uso de programas de cómputo (Gettys et al., 1991).

 

CONCLUSIONES.

El modelo planteado por Orskov y McDonald (1979) para estimar los parámetros de degradabilidad ruminal fue originalmente propuesto por Johann Heinrich von Thünen (1930) para el estudio de las relaciones de producción agrícola denominando a kd como tasa instantánea de disminución en la productividad marginal. En el estudio de la cinética de la degradabilidad de fracciones nutricionales en el rumen, esta constante, al igual que la constante de pasaje ruminal (kp), han sido mal definidas y erróneamente interpretadas como velocidades de degradación y de paso, respectivamente. Matemáticamente ha sido demostrado que estas constantes representan la relación entre la aceleración y la velocidad de degradación y pasaje ruminal, respectivamente (Correa, 2005). Por tal razón, la kd y la kp deben ser denominadas constantes de la cinética de degradación y de pasaje ruminal, respectivamente. Con base en estas características se plantea una propuesta basada en métodos numéricos para el cálculo de la DEb que permite obtener datos confiables y coherentes con las bases matemáticas de la cinética de la degradación y el pasaje ruminal de las fracciones nutricionales.

 

AGRADECIMIENTOS

A los profesores Fernando Puerta Ortiz y Jorge Cossio Betancur (Facultad de Ciencias, Departamento de Matemáticas de la Universidad Nacional de Colombia, sede Medellín), por su orientación matemática.

 

BIBLIOGRAFÍA

Bach, A., M.D. Stern, N.R. Merchen and J.K. Drackley. 1998. Evaluation of selected mathematical approaches to the kinetics of protein degradation in situ.  J. Anim. Sci. 76: 2885–2893.        [ Links ]

Correa, H.J. 2004. Rumenal: procedimiento para estimar los parámetros de cinética ruminal mediante la función Solver de Microsoft Excel®. Revista Colombiana de Ciencias Pecuarias 17(3): 250–254.        [ Links ]

Correa, H.J. 2005. Origin and comprehensive study of Thünen´s model to analyze data from in situ rumen degradability technique. Revista Colombiana de Ciencias Pecuarias 18(1): 80–87.        [ Links ]

Gettys, W.E., F.J. Keller y M.J. Skove. 1991. Física clásica y moderna. McGraw-Hill, Madrid. 1241 p.        [ Links ]

Grovum, W.L. and V.J. Williams. 1973. Rate of passage of digesta in sheep. 4. Passage of marker through the alimentary tract and the biological relevance of rate constants derived from changes in concentration of marker in faeces. British Journal of Nutrition 30(2): 313-329.        [ Links ]

Kutzler, B. and T. Boykett. 1996. Improving mathematics teaching with DERIVE: a guide for teachers. Lancashire, U.K: Chartwell-Yorke. 185 p.        [ Links ]

National Research Council. 2001. Nutrient Requirements of Dairy Cattle, 7th rev ed Washington, D.C: National Academy Press. 381 p.        [ Links ]

Orskov, E. R. and I. McDonald. 1979. The estimation of protein degradability in the rumen from incubation measurements weighted according to rate of passage. Journal of Agriculture Science 92(2): 492-503.        [ Links ]

Thünen, J.H. von. 1930. Der isolierte staat in beziehung auf landwirthschaft und national okonomie. 3 volumes. Jena, Germany : Fischer. Citado por: Humphrey, T.M. 1997. Algebraic production functions and their uses before Cobb-Douglas. Federal Reserve Bank of Richmond Economic Quarterly 83(1): 51–83.        [ Links ]