EVALUACIÓN DE DOS MÉTODOS DE ESTABILIDAD FENOTÍPICA A TRAVÉS DE VALIDACIÓN CRUZADA

EVALUATION OF TWO METHODS OF PHENOTYPIC STABILITY THROUGH CROSS-VALIDATION

 

Jairo Alberto Rueda Restrepo¹ y José Miguel Cotes Torres²

 

¹ Profesor Asistente. Universidad Nacional de Colombia, Sede Medellín. Facultad de Ciencias Agropecuarias. A.A. 1779. Medellín, Colombia. <jarueda@unal.edu.co>
² Profesor Asociado. Universidad Nacional de Colombia, Sede Medellín. Facultad de Ciencias Agropecuarias. A.A. 1779. Medellín, Colombia. <jmcotes@unal.edu.co>

 

Recibido: Mayo 18 de 2007; Aceptado: Septiembre 7 de 2009.

---

Resumen. Una de las principales preocupaciones de los fitomejoradores es la evaluación de la estabilidad fenotípica mediante la realización de pruebas regionales o multiambiente. Existen numerosos métodos propuestos para el análisis de estas pruebas regionales y la estimación de la estabilidad fenotípica. En este trabajo se compara el método de regresión propuesto por Eberhart y Russell y el de componentes de varianza propuesto por Shukla, siguiendo un esquema de validación cruzada. Para ello fueron utilizados datos provenientes de 20 pruebas multiambiente de maíz, cada una con nueve genotipos, plantadas bajo un diseño en bloques completos al azar con cuatro repeticiones. Se encontró que el mejor modelo para predecir el rendimiento futuro de un genotipo en un determinado ambiente es el método de Eberhart y Russell, presentando un valor de raíz cuadrada del cuadrado medio de predicción 2,21% menos que el método de Shukla, con una consistencia en la predicción de 90,6%.

Palabras claves: Interacción genotipo-ambiente, adaptabilidad fenotípica, varianza de Shukla, pruebas regionales.

Abstract. One of the most important topics of plant breeders is to evaluate the phenotypic stability through regional trials or multi-environment trials. There are many methods proposed to analyze those trials and to estimate the phenotypic stability. This paper compares the regression method proposed by Eberhart and Russell and the components of variance proposed by Shukla, according to a cross-validation methodology. Data from 20 multi-environment corn tests, each one with nine genotypes, planted under a randomized complete block design with four replications, were used. It was found that the best model to predict the future performance of a genotype is the method of Eberhart and Russell, showing a root square value of the prediction medium 2,21% less than Shukla´s method , which a prediction consistence of 90.6%.

Key words: Genotype-environment interaction, phenotypic adaptability, Shukla's variance, regional trials.

---

 

Actualmente existen muchas metodologías de análisis de estabilidad fenotípica. El método tradicional consiste en el análisis conjunto de los experimentos, considerando todos los ambientes y el posterior desdoblamiento de la suma de cuadrados de efectos de los ambientes y de la interacción genotipo-ambiente (IGA) (Yates y Cochran, 1938; Cornelius et al., 1994; Kang y Magary, 1996; Cruz y Regazzi, 1994; Vallejo y Estrada, 2002; Cotes et al., 2006; Edwards y Jannink, 2006; Piepho, 2009). La variación de ambientes dentro de cada genotipo es utilizada como un estimado de la estabilidad, de tal forma que el genotipo que tenga un menor cuadrado medio en los ambientes será considerado el más estable (Cruz y Regazzi, 1994).

Los estudios de la interacción genotipo-ambiente proveen información sobre el comportamiento de cada genotipo frente a variaciones ambientales. Por esto, se realizan análisis de estabilidad y adaptabilidad fenotípica, mediante los cuales es posible identificar cultivares de comportamiento relativamente previsible.

Los métodos propuestos por Finlay y Wilkinson (1963) y el mejorado por Eberhart y Russell (1966), se basan en el análisis de regresión lineal, que mide la respuesta de cada genotipo con las variaciones ambientales.

La regresión de Eberhart y Russell difiere de la regresión de Finlay y Wilkinson, en que las desviaciones dij tienen una varianza separada para cada genotipo (Piepho, 1999). Estas varianzas pueden ser denotadas como: s²_d(t) y s²_f(t) (Piepho, 1999). Los parámetros de estabilidad se estiman por la regresión sobre un índice ambiental para cada variedad (genotipo). Estos parámetros son definidos por el modelo (Eberhart y Russell, 1966):

Con i=1,...,v (genotipos); j=1,...,n (ambientes); µi la media de cada cultivar y ßi los coeficientes de regresión que miden la respuesta de cada genotipo al cambio en índice ambiental; Ij es el índice ambiental obtenido como el promedio de todas las variedades en el j-ésimo ambiente menos la gran media o media general (Eberhart y Russell, 1966). Los coeficientes de regresión ßi de este modelo son conocidos como el parámetro de adaptabilidad, mientras que la suma de las desviaciones (valor observado respecto del valor estimado) proveen una aproximación al parámetro de estabilidad fenotípica dado por (Eberhart y Russell, 1966):

donde, S²_e/r , es el error residual del análisis de varianza (ANAVA) combinado (que incluye todas las pruebas regionales):

Así, este modelo permite una forma de partir la interacción genotipo-ambiente de cada cultivar en dos partes: a) desviación debida a la respuesta de la variedad al cambio en índice ambiental (suma de cuadrados de la regresión) y b) desviaciones no explicadas por el modelo; las cuales son una aproximación a la estabilidad fenotípica del cultivar. De esta forma los cultivares pueden clasificarse como predecibles o no predecibles, y estables o inestables.

Por otro lado el modelo propuesto por Shukla (1972), estima los componentes de varianza dentro del efecto de la interacción genotipo ambiente, con un modelo lineal de la forma propuesta por Piepho (1999):

donde yijk (i=1,.,I genotipos; j=1,.,J ambientes; k=1,.,K repeticiones) es la respuesta en la k-ésima repetición del i-ésimo genotipo en el j-ésimo ambiente, µ es la media general, gi el efecto del i-ésimo genotipo, ej es el efecto del j-ésimo ambiente, (ge)ij es el efecto de la interacción del genotipo i en el ambiente j, y eijk es el término del error experimental asociado a yijk (Shukla, 1972).Los efectos aleatorios rjk, ej, (ge)ij y eijk y son asumidos como independientes, distribuidos con media cero y varianzas s_rjk, s_Ej, s_(gE)j (estabilidad de varianzas) y s_eikj respectivamente (Piepho, 1999). Los cultivares con valores no significativamente diferentes de cero para s_(gE)ij, son considerados genotipos estables.

La metodología propuesta por Shukla, surge como respuesta al problema de que la caracterización de los genotipos con base en los coeficientes de regresión (como es el caso del modelo Eberhart y Russell), puede no ser muy efectiva cuando solo una pequeña fracción de esta suma de cuadrados (IGA), se puede atribuir a la heterogeneidad entre las regresiones.

Para comparar dos modelos existen numerosas técnicas estadísticas, dentro de las cuales se encuentra la validación cruzada. Esta técnica se recomienda como una de las mejores formas de probar un modelo, pues se introduce un sesgo al probar la validez de un modelo con los mismos datos con los que fueron estimados sus parámetros (Cooil et al., 1987). La validación cruzada muchas veces es tomada como sinónimo de partición de los datos, pero según estos autores, existen tres aproximaciones a la misma: i) partición de los datos, la cual separa la estimación del modelo de la validación, ii) métodos de uso repetido de la muestra tales como el "jackknife", los cuales se concentran principalmente en la estimación de parámetros y, iii) los métodos que estos mismos autores llaman métodos simultáneos, en los cuales se estima y se valida el modelo.

Usualmente, el investigador divide la muestra en dos partes y a continuación, usa una parte llamada muestra de estimación para calcular los parámetros del modelo. La ecuación resultante es usada para predecir los valores de la variable dependiente del resto de las observaciones -las que se dejaron por fuera- (Steckel y Vanhonaker, 1993).

Por otro lado, las técnicas de dividir la muestra en partes como las descritas anteriormente, son conocidas como técnicas de remuestreo y además de permitir la comparación de dos modelos estadísticos, permiten la estimación de parámetros de interés en cada modelo. Así, la técnica "jackknife" puede ser usada para estimar la precisión de coeficientes, sobre todo cuando no se conoce la distribución exacta para estimar la varianza de los parámetros y/o la distribución muestral es desconocida. Esta técnica, usada para responder a la pregunta "¿Qué tan preciso es el estimador?" puede ser usada para estimar sesgo o error estándar, mas no para estimar intervalos de confianza (Efron, 1982). Manly (1996), establece que la técnica falla cuando el estimador no se distribuye normalmente; sin embargo, puede mejorar su desempeño cuando se utilizan transformaciones que lo normalicen; este autor sugiere trabajar con la transformación logaritmo natural. Dixon (1993) añade que intervalos de confianza basados en error estándar estimado con "jackknife" asumen que el estadístico tiene una distribución normal y que si esta distribución es asimétrica o tiene colas pesadas, los intervalos son imprecisos.

La idea básica en el proceso "jackknife" es que el sesgo y el error estándar de un estadístico pueden ser estimados por el recálculo de éste en un subgrupo de los datos (Dixon, 1993), lo que lo convierte en una forma de validación cruzada. Algunos resultados teóricos muestran que en muestras extremadamente grandes las técnicas de "Bootstrap" y "jackknife" arrojan resultados similares (Efron, 1982 citado por Dixon, 1993).

La palabra "jackknife" describe un gran número de herramientas que pueden ser usadas en muchas tareas, si bien, raramente es ideal para alguna de ellas (Manly, 1996). La palabra "jackknife" fue propuesta por Tukey en 1958 para usar en estadística, al describir una aproximación general para pruebas de hipótesis y el cálculo de intervalos de confianza en situaciones en las cuales otros métodos mejores no pueden ser fácilmente usados.

Una forma de justificar el uso de los estimadores "jackknife" es pensar en términos de lo que se hace con la estimación de la media, pero desde un punto de vista inusual. Para ello se supone que se tiene una muestra aleatoria de n valores X1, X2, ...,Xn y se estima la media de la población:

Luego se asume que este promedio es calculado otra vez, pero con la j-ésima observación perdida, arrojando:

Las dos últimas ecuaciones pueden ser resueltas para Xj resultando:

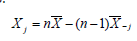
De esta forma, es posible determinar el valor de Xj de la media general y la media excluida la j-ésima observación.

En general, se asume que un parámetro ? es estimado por alguna función de n valores muestrales, este estimado puede ser denotado por Ê(X1, X2,...,Xn) , y escrito brevemente por Ê . Con la exclusión de Xj, el estimado parcial de ? es Ê-J. Por analogía, existe un conjunto de "pseudo valores"

Para j = 1,2,...,n. Estos pseudo valores juegan el mismo papel que los Xj en la estimación de la media y el promedio de los pseudo valores.

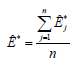
Es el estimador "jackknife" de ? (Manly, 1996). Si se tratan los pseudo valores como una muestra aleatoria de estimaciones independientes, entonces se sugiere que la varianza de este estimador "jackknife" puede ser calculado por S2/n, donde S2 es la varianza muestral de los pseudo valores estimados. Avanzando un poco más, se sugiere que un intervalo al (1-a)100% para ? está dado por , donde es el valor que excede la probabilidad de a/2 en la distribución de t con n-1 grados de libertad (Manly, 1996).

Se puede decir que se transforma un problema de estimación en la tarea de hallar un promedio muestral. Todo lo que se necesita es que el estimador del parámetro usual de interés sea una función de los valores de la muestra. En particular, los pseudo valores posiblemente están correlacionados y así la varianza estimada del estimador "jackknife" presenta alguna forma de sesgo y particularmente, predecir si es el caso o no, es teóricamente difícil. Usualmente la varianza del estimador "jackknife" necesita ser justificada por estudios numéricos de rango antes que pueda ser confiable.

Este trabajo tuvo como objetivo comparar por validación cruzada la predicción del rendimiento bajo los modelos de estabilidad fenotípica de Eberhart y Russell (1966) y Shukla (1972), los cuales son ampliamente utilizados por los mejoradores de plantas. Adicionalmente se obtuvieron los estimadores "jackknife" para los parámetros de estabilidad de cada uno de los modelos.

 

MÉTODOS

Se utilizó el conjunto de datos CIMMYT EVT16B, correspondiente a 20 pruebas multiambientales, establecidas bajo un diseño en bloques completos al azar con cuatro repeticiones, para nueve líneas elites de mejoramiento, los cuales han sido utilizados por Cornelius et al. (1992), Cornelius et al., 1996, y Cornelius y Crossa (1999), y Cotes et al. (2006) aplicando diferentes metodologías de análisis.

Inicialmente se realizó un análisis combinado de las pruebas regionales según el siguiente modelo:

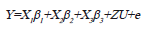
Donde Y es el vector de observaciones (n × 1), X1 y ß1 son la matriz de diseño (n × a) y el vector (ax1) de efectos fijos de los ambientes (j=1,...a); X2 y ß2 son la matriz de diseño (n × g) y el vector (g × 1) de efectos fijos de los genotipos (i=1,...g); X3 y ß3 son la matriz de diseño (n × ag) y el vector (agx1) de efectos fijos de la interacción genotipo por ambiente, Z y U son la matriz de incidencia (n × ab) y el vector (abx1) de efectos aleatorios de los bloques (r=1,...,b) dentro de los genotipos, y e es el vector (n × 1) asociado al error. Se supone que 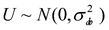y .

Para la implementación de las metodologías de Eberhart y Russell y varianza de Shukla, se utilizó la varianza s² estimada del modelo anterior.

Modelo de Eberhart y Russell. Se utilizó el modelo basado en promedios de genotipos por ambientes de la siguiente manera:

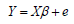
Donde Y es el vector (ag × 1) de promedios de los genotipos en cada ambiente, X es la matriz de diseño bloque diagonal (ag × 2g), ß es el vector de coeficientes de regresión (2g × 1) y e es el vector (ab × 1) de efectos del error.

Así, el modelo se puede expresar como:

Donde y_i es el vector de medias de cada ambiente para el i-ésimo genotipo, A es el vector de índices ambientales para el ambiente j-ésimo, 1a es un vector columna de unos, de tamaño "a", ß0i (el intercepto para cada genotipo) es el promedio de rendimiento para el i-ésimo genotipo, ß1i (el coeficiente de regresión) es el índice de adaptabilidad asociado al genotipo i, y ei es el vector de efectos del error para el i-ésimo genotipo. Se asume .

Modelo de Shukla. Para este método también se utilizó el modelo de promedios de genotipos por ambiente de la siguiente forma:

Donde Y es el vector (ag × 1) de promedios de los genotipos en cada ambiente, X1 y ß1 son la matriz de diseño (ag × a) y el vector (a × 1) de efectos fijos de los ambientes, X2 y ß2 son la matriz de diseño (ag × g) y el vector de efectos fijos de los genotipos; e= [e'i ,...,e'i ,...e'g ] de efectos aleatorios de la interacción genotipo por ambiente. Se asume que .

Validación cruzada. La base de datos fue dividida usando un esquema de muestreo aleatorio que extraía, de cada celda de la tabla de rendimientos genotipo por ambiente, una repetición. Para ello fue programado un MACRO en SAS que elimina a cada combinación genotipo por ambiente, alguna de sus cuatro repeticiones. Un billón (1099511627776) de posibles subconjuntos puede ser generado para estimar de nuevo la estabilidad.

Los posibles subconjuntos diferentes que se pueden formar fueron muestreados de forma aleatoria, cuidando de no repetir una combinación de exclusiones. Ésta forma de muestreo hace del procedimiento una forma de estimación tipo "jackknife". Para efectos de garantizar la estimación, siempre con una combinación diferente de repeticiones, fue asignado a cada una de éstas una identificación numérica. El proceso se realizó 25.000 veces.

Estimador "jackknife". Quenuoille (1956) señala que el reemplazar un estimador por su versión "jackknife" tiene el efecto de remover sesgo de orden 1/n. Así, asuma que el valor esperado (la media) del estimador Ê de ?, basado en toda la muestra, sea q(1+A/n). Entonces el valor esperado del estimador parcial Ê-j , con la j-ésima removida, es q{(1+A/(n)}. Se sigue que el valor esperado del j-ésimo pseudo valor como es definido por la ecuación (16) (Manly, 1996) es:

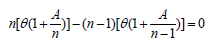
Con el factor de sesgo simplificado. Así, para cada valor de j, y consecuentemente, para cada valor esperado de Ê*, el promedio de los pseudovalores es también q.

Esta cualidad de los estimadores "jackknife" se utilizó para los estimadores de estabilidad genotípica de Shukla y de Eberhart y Russell. En el Anexo 1 se encuentra el código para el programa SAS® con el que se realizaron los análisis completos y el proceso de obtener la estimación "jackknife" de las medidas de estabilidad mencionadas.

Rutina de cómputo. Para realizar el análisis se implementó un programa SAS® que realiza los siguientes procesos (Anexo 1):

En el primer módulo de ese programa se escriben las operaciones de lectura y ordenación de la base de datos, se toma una muestra de n-1 elementos (el programa extrae subconjuntos siempre diferentes de este tamaño) y se llaman las rutinas almacenadas en el segundo módulo.

En el segundo módulo, se calculan los estadísticos de estabilidad y se estiman los valores esperados del rendimiento para cada genotipo y con éstos, la diferencia respecto de los valores estimados con todos los datos. Tanto los parámetros, como la diferencia respecto de la información completa, son almacenados en archivos separados; el programa retorna estos valores al módulo principal (Teste.sas). En este punto se repite el proceso hasta el número especificado de muestreos.

Comparación de modelos y estimación de parámetros. El proceso de validación cruzada permite obtener la diferencia entre el valor observado y el estimado (independientemente). En el conjunto de tales diferencias, cada una se elevó al cuadrado y se acumuló para cada método el estadístico RDMSP denominado así, por la siglas en inglés de "Root of mean squared error of prediction".

Con el conjunto de parámetros estimados se calcularon los percentiles 2,5 y 97,5 que permitieron hallar intervalos de confianza tipo "jackknife" para los parámetros de estabilidad vía Shukla (1972) y Eberhart y Russell (1966).

Posteriormente, se realizó la comparación de la eficiencia relativa de los dos métodos mediante los valores de RDPMSShukla y RDPMSEberhart&Russell. El método que presente el menor valor será el mejor método, ya que presenta una mejor predicción.

Adicionalmente, con el fin de observar la consistencia en la predicción, se obtuvo la frecuencia fi,, en que el método de ER arrojará menor diferencia que Shukla (1972). Dicho conteo se expresó como una frecuencia relativa en porcentaje:

 

RESULTADOS Y DISCUSIÓN

Se realizaron 25.000 muestreos excluyendo alguna combinación diferente de repeticiones eliminadas en cada celda de la tabla de interacción genotipo por ambiente. El tiempo real de computo se estimó en 28 horas en una máquina Pentium IV, con una giga de memoria RAM.

Con intervalos relativamente equivalentes en amplitud, el estadístico RDMSP para el método de Eberhart y Russell, presenta un valor 2,21% menor que el método de Shukla por lo que es más efectivo al estimar el futuro valor de los rendimientos de un genotipo en un determinado ambiente (Tabla 1). La dispersión en ambos estadísticos es aproximadamente la misma, pero los intervalos no se traslapan por lo que se puede inferir la existencia de una diferencia significativa entre los RDPMS de ambos métodos. Teniendo en cuenta la consistencia de la predicción se encontró que el 90,6% de las 25000 veces que se aplicó el procedimiento, la metodología de Eberhart y Russell, fue más precisa que la de Shukla, lo cual fortalece la preferencia del modelo de Eberhart y Russell frente al modelo de Shukla.

Tabla 1. Estimativas e intervalo de confianza de 95% para la raíz cuadrada del cuadrado medio del error de predicción (RDMSP) al realizar 25000 iteraciones del proceso de validación cruzada sobre los datos de maíz.

Cornelius et al. (1996) y Cornelius y Crossa (1999) encontraron que para modelos AMMI ("AdditiveMain and Multiplicative Interaction"), COMM ("Complete multiplicative model"), SREG ("Site regression"), GREG ("Genotype regression") y SHMM ("Shifted multiplicative model") los valores de RDPMS del mejor modelo truncado para este conjunto de datos fueron 915, 911, 908, 907 y 906, respectivamente. Así, la metodología de Eberhart y Russell, y la propuesta por Shukla, tienen mayores valores de RDPMS que los presentados por los modelos que consideran efectos multiplicativos, confirmando la tendencia actual de los mejoradores de plantas a utilizar modelos multiplicativos seguidos de análisis de "biplot" (Cornelius et al., 1992; Yan et al., 2007).

Utilizando el esquema de validación cruzada se estimaron por el método de "jackknife" los intervalos de confianza para los parámetros de estabilidad fenotípica de Eberhart y Russell (Figura 1 y 2) y de Shukla (Figura 3). Como se observa, los intervalos son bastante amplios, lo cual concuerda con lo encontrado por Efron (1982). Sin embargo, son una buena alternativa para su utilización, en este caso, porque éstos dan una buena respuesta al problema de las aproximaciones en la distribución de los parámetros presentados originalmente por los autores de estos métodos.

Figura 1. Coeficiente de regresión para el modelo de Eberhart y Russell para nueve genotipos de maíz. Las barras indican el intervalo de confianza de 95% por la metodología jackknife. Los genotipos que cruzan la línea de referencia en uno son, considerados como de amplia adaptabilidad.

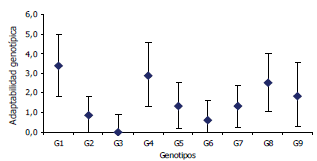
Figura 2. Desvíos de la regresión (1×105) para el modelo de Eberhart y Russell para nueve genotipos de maíz. Las barras indican el intervalo de confianza de 95% por la metodología jackknife. Los genotipos que cruzan la línea de referencia en cero, son considerados como estables

Figura 3. Varianza de estabilidad fenotípica de Shukla (1×105) para nueve genotipos de maíz. Las barras indican el intervalo de confianza de 95% por la metodología jackknife. Los genotipos con los valores más próximos a cero, son considerados estables.

Según los valores de adaptabilidad fenotípica, ß1i , los genotipos G4, G5 y G9 presentan mejor respuesta en ambientes favorables ya que presentan un coeficiente de regresión significativamente superior a la unidad (Vallejo y Estrada, 2002); los genotipos G7 y G8 tienen mejor respuesta en ambientes desfavorables por presentar coeficientes de regresión menores que uno. Los demás genotipos, es decir, G1, G2, G3 y G6 son clasificados como de amplia adaptabilidad ya que el coeficiente de regresión no es significativamente diferente de uno (Figura 1).

Teniendo en cuenta los valores de estabilidad fenotípica según la metodología de Eberhart y Russell, los genotipos más estables son G2, G3 y G6 (Figura 2), ya que los intervalos de confianza obtenidos por "jackknife" incluyen en su límite inferior el cero. Así estos genotipos serían los cultivares a seleccionar por presentar una adaptabilidad amplia y una alta estabilidad fenotípica.

Por otro lado, analizando la varianza de estabilidad fenotípica de Shukla, se encontró que los genotipos con menor varianza son G2, G3 y G6, seleccionando estos genotipos como los más estables (Figura 3).

Cotes et al. (2006) aplicando la metodología bayesiana en la estimación de la varianza de estabilidad fenotípica de Shukla para este conjunto de datos, encontraron que los genotipos G2, G3, G6, y G7 fueron los más estables, con valores de 1760, 1256, 1894, 1975, respectivamente. Cornelius et al. (1996) aplicando el modelo GREG, e inspeccionando los dos primeros componentes multiplicativos, encuentran que los genotipos que presentan altos rendimientos en promedio (G4, G5 y G6) tienen un desempeño pobre en la localidad 8, donde los genotipos G1 y G2, con bajos rendimientos promedios, presentan buen desempeño.

Así, la metodología de "jackknife" y la metodología bayesiana, tienen poca diferencia en lo referente a la selección de los genotipos. Los valores estimados de la varianza de estabilidad fenotípica y sus respectivos intervalos de alta probabilidad a posteriori obtenidos por la metodología bayesiana (Cotes et al., 2006), son menores que los encontrados por "jackknife"; sin embargo, el tiempo computacional de esta última metodología es mucho menor. En la metodología GREG, el genotipo G6 se presenta como un cultivar de adaptación específica, mientras que, tanto en el modelo de Eberhart y Russell como en el de Shukla, este genotipo presenta adaptación amplia y buena estabilidad fenotípica. Esto posiblemente se debe a la subjetividad de la interpretación de los componentes en los modelos multiplicativos (Cornelius y Crossa, 1995) y potencialmente constituye una desventaja de estos métodos, opacando la capacidad predictiva mostrada en la validación cruzada.

Las diferencias encontradas en la predicción del rendimiento por la metodología de Eberhart y Russell y la varianza de estabilidad fenotípica de Shukla, no afectaron la elección de genotipos, siendo seleccionados, por ambos métodos, los genotipos G2, G3 y G6. Sin embargo, esto puede ser una particularidad de este conjunto de datos, por lo que se recomienda el análisis de ambas metodologías, por validación cruzada, en otros estudios.

 

CONCLUSIONES

Utilizando la metodología de validación cruzada, el método de Eberhart y Russel, fue consistentemente mejor en la predicción del rendimiento que el método de Shukla, por lo que éste puede ser considerado como el más efectivo, al estimar el futuro valor de los rendimientos de un genotipo en un determinado ambiente.

Los modelos estadísticos considerados en este estudio para el análisis de pruebas regionales, mostraron ser aproximadamente, consistentes en cuanto a la selección de los genotipos con mayor estabilidad fenotípica, en particular los genotipos G2, G3 y G6, son seleccionados por ambas metodologías.

La metodología "jackknife" es una alternativa aplicada al análisis de pruebas regionales, computacionalmente viable, frente a otras metodologías estadísticas más complejas y permite una adecuada selección de genotipos.

La aplicación de la validación cruzada en pruebas regionales, permitió comparar de una forma eficiente dos modelos de estabilidad fenotípica que difieren en el número de parámetros a estimar y en la interpretación de los mismos, por lo cual es recomendable utilizar la validación cruzada para seleccionar el mejor modelo de análisis de pruebas regionales, bajo las condiciones particulares de cada conjunto de datos.

 

ANEXO 1

 

BIBLIOGRAFÍA

Cooil, B., R. Winer and D. Rados. 1987. Cross-Validation for prediction. Journal of Marketing Research 24: 271-279.        [ Links ]

Cornelius, P.L. and J. Crossa. 1995. Shrinkage estimators of multiplicative models for crops cultivar trials. Technical Report No. 352, University of Kentuky. Department of Statistics. Lexington, Kentucky.        [ Links ]

Cornelius, P.L. and J. Crossa. 1999. Prediction assessment of shrinkage estimators of multiplicative models for multi-environment cultivar trials. Crop Science 39: 998–1009.

Cornelius, P.L., M.S. Seyedsadr and J. Crossa. 1992. Using the shifted multiplicative model to search for separability in crop cultivar trials. Theoretical an Applied Genetics 84(1-2): 161–172

Cornelius, P.L., J. Crossa, and M.S. Seyedsadr. 1996. Statistical test and estimator of multiplicative models for genotype by environment interaction. pp. 199-234. In: Kang, M.S. and H.G. Gauch (eds.). Genotype by environment interaction. CRC press, Boca Raton U.S.A. 416 p.        [ Links ]

Cotes, J.M., J. Crossa, A. Sanches and P.L. Cornelius. 2006. A bayesian approach for assessing the stability of genotypes. Crop Science 46: 2654–2665

Cruz, C.D. e J. Regazzi. 1994. Modelos biométricos aplicados ao melhoramiento genético. Segunda edição. Imprensa Universitária da Universidade Federal de Viçosa. 390p.        [ Links ]

Dixon, P.M. 1993. The bootstrap and the jacknife: Describing the precision of ecological indices, In: Scheiner, S. and J. Gurevitch (ed.). Design and analysis of ecological experiments. Chapman and Hall, New York. USA. 445 p.        [ Links ]

Eberhart, S.A. and W.A. Russell. 1966. Stability parameters for comparing varieties. Crop Science 6: 36-40.        [ Links ]

Edwards, J.W. and J.-L. Jannink. 2006. Bayesian modeling of heterogeneous error and genotype × environment interaction variances. Crop Science 46:820-833.        [ Links ]

Efron, B. 1982. The jacknife, the bootstrap and others resampling plans. Society of Industrial and Applied Matematics. CBMS-NSF Monograph 38 p.        [ Links ]

Finlay, K.W. and G.N. Wilkinson. 1963. The analysis of adaptation in a plant breeding programme. Australian Journal of Agricultural Research 14: 742-754.        [ Links ]

Kang, M.S. and R. Magari. 1996. New developments in selecting for phenotypic stability in crop breeding. pp. 1-14. In: Kang M.S. and H.G. Gauch (ed.). Genotype by Environment Interaction. CRC press. Boca Raton USA. 416 p.        [ Links ]

Manly, F.J. 1996. Randomization, bootstrap and Montecarlo methods in biology. Second edition. Chapman and Hall, London. 455 p.        [ Links ]

Piepho, H.P. 1999. Stability analysis using the SAS system. Agronomy Journal 91: 154-160.        [ Links ]

Piepho, H.P. 2009. Data transformation in statistical analysis of field trials with changing treatment variance. Agronomy Journal 101: 865-869        [ Links ]

Quenuoille, M.H. 1956. Notes on bias in estimation. Biometrika 43(3-4): 353-360.        [ Links ]

Shukla, G.K. 1972. Some statistical aspects of partitioning genotype-environmental components of variability. Heredity 29: 237-245.        [ Links ]

Steckel, J.H. and W.R. Vanhonacker. 1993 Cross-validating regression models in marketing research. Marketing Science 12(4): 415-427.        [ Links ]

Vallejo, F.A. y E.I. Estrada. 2002. Mejoramiento genético de plantas. Universidad Nacional de Colombia, Sede Palmira. 401 p.        [ Links ]

Yan, W., M.S. Kang, B. Ma, S. Woods and P.L. Cornelius. 2007. GGE biplot vs. AMMI analysis of genotype-by-environment data. Crop Science 47: 643-653.        [ Links ]

Yates, F. and W.G. Cochran. 1938. The analysis of groups of experiments. The Journal of Agricultural Science 28: 556-580.        [ Links ]