¹ Departamento de Física, Universidad Nacional de Colombia, Bogotá. Email: remartinezm@unal.edu.co

Resumen

El descubrimiento del Higgs en el colisionador de hadrones (LHC) en el CERN con una masa de 125 GeV es fundamental para entender la generación de la masa de las partículas elementales y el origen de la gravedad. El Higgs es una pieza clave en el Universo porque es un candidato para materia oscura y poder entender la dinámica estelar. Peter Higgs lo postuló en 1964 y sólo hasta 2012 se pudo observar en los detectores ATLAS Y CMS del LHC.

Palabras clave: Partícula de Higgs.

Abstract

The discovery of the Higgs in the Large Hadron Collider (LHC) at CERN with a mass of 125 GeV is fundamental to understand the mass generation of elementary particles and origin of gravity. The Higgs is a key in the universe because it is a candidate for dark matter to understand the stellar dynamics. Peter Higgs postulated it in 1964 and until 2012 was observed in ATLAS and CMS detectors at the LHC.

Key words: Higgs' particle.

Introducción

El aire es un gas cuyas moléculas se mueven erráticamente obedeciendo la distribución de Maxwell Boltzmann. Cuando el ala de un avión pasa a través de este gas, sus moléculas golpean el ala. Entre mayor sea la velocidad relativa de las moléculas respecto al ala, menor es la presión que hace el gas al ala. Las diferencias de curvaturas en el ala, inferior-superior, genera una diferencia de presión, que se convierte en una fuerza de sustentación, la cual, al ser mayor que el peso del avión hace que éste pueda volar. De aquí se desprende el concepto de viscosidad del aire como un efecto colectivo de moléculas moviéndose y entrelazándose, generado fuerzas de fricción y de sustentación.

Entre mayor sea la temperatura del gas mayor sería la agitación térmica del aire y mayor el golpeteo de las moléculas del aire sobre el ala del avión. Por ejemplo, en Barranquilla el efecto aerodinámico es mayor que en Bogotá y podemos asociar, con la temperatura, la capacidad que tiene el aire de generar mayor o menor fuerza de sustentación [1].

Cuando las partículas tratan de viajar por el Universo se encuentran con el campo de Higgs adquiriendo automáticamente masa, inercia, resistencia a las fuerzas, pero también gravedad. En este sentido podríamos hacer el símil con la aerodinámica, donde el aire genera la viscosidad que induce la resistencia cuando los cuerpos se muevan a través del fluido, pero también la fuerza de sustentación. Sólo es un símil, porque la aerodinámica hace referencia a un fenómeno de transporte de moléculas y es una teoría clásica, en cambio el campo de Higgs es un ente cuántico.

El Higgs [2], la partícula de Dios, la podemos pensar como el equivalente de este gas, pero es un efecto puramente cuántico. Se crean y se aniquilan interactúando con las partículas ordinarias, la materia, haciendo que éstas adquieran masa. Dependiendo de la forma de interacci ón, las partículas adquieran mayor o menor masa, la cual está asociada a los efectos gravitacionales y los efectos inerciales, es decir, la capacidad de atraerse o a resistirse a experimentar aceleraciones debidas a fuerzas.

Los neutrinos interactúan débilmente con el campo de Higgs y su masa es prácticamente nula. En cambio el electrón interactúa más fuertemente con el campo de Higgs y su masa es mayor. El fotón no interactúa con el campo de Higgs y su masa es nula. Es decir, que tan grande sea la masa de la partícula nos está indicando que tan fuerte es el efecto de interacción con el campo del Higgs.

Curiosamente el Higgs aparece masivo en el Universo cuando éste se expande y comienza el proceso de enfriamiento, generándose una transición de fase, similar a la transición del agua del estado líquido al estado sólido. En dicha transición de fase se genera una interacción entre campos la cual induce una masa al Higgs. En el agua aparecen los cristales. Dicha partícula automáticamente comienza a interactuar con la materia. Antes todas las partículas tenían energía y viajaban a la velocidad de la luz. Después de la transición las partículas interactúan con el Higgs y adquieren masa y dejan de viajar a la velocidad de la luz. Además las nuevas partículas masivas comienzan a generar atracción gravitacional. Con el enfriamiento del Universo y la atracción gravitacional sumado millones y millones de años se formaron las galaxias, estrellas, etc.

Podríamos hacer un símil con la viscosidad del aire y el campo cuántico asociado al Higgs el cual genera una "viscosidad" que termina dotando de masa a las partículas. La única que no adquirió masa fue el fotón, los rayos de luz, por esto pueden ir hasta el confín del Universo. Es como si el fotón fuera completamente transparente al campo de Higgs.

El Universo es una sopa de partículas que se mueven a la velocidad de la luz, pero éste se está expandiendo y se está enfriando. Una de estas partículas, que identificamos como una partícula escalar de espín cero, el Higgs, obedece una ecuación y tiene un potencial de interacción con dos parámetros que dependen de la temperatura del Universo,

En la ecuación de movimiento del campo de Higgs el parámetro 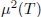se interpreta como la masa inercial de la partícula, representa el campo del Higgs y es término que nos indica como autointeractúa el campo del Higgs consigo mismo. En el Universo temperado dichos parámetros son positivos; pero cuando éste se enfría ocurre una transición de fase y uno de ellos cambia de signo, 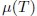. Justo en ese momento, en la ecuación de movimiento del Higgs, aparece una masa y decimos el Higgs se hizo masivo. Además todas las partículas que interactúan con el campo del Higgs también les aparecer á una masa. Pasamos de un Universo lleno de energía y partículas moviéndose a la velocidad de la luz, a un Universo de partículas relativistas y masivas. En el símil con el agua decimos que se comienzan a formar los cristales y el agua deja de ser líquida.

¿De dónde sale la masa del Higgs?

Aparece de la autointeracción del Higgs consigo mismo después de la transición de fase. Antes de la transici ón de fase el Higgs interactúa consigo mismo pero los parámetros de la interacción no son adecuados para que se genere la masa del Higgs. Después de la transición los parámetros de la autointeracción cambian y aparece la masa del Higgs. Por ejemplo, en la transición del agua de la fase líquida a la sólida, podemos cambiar el punto de congelamiento poniendo sal. Existen unos parámetros termodinámicos que dependen de la temperatura y estos van cambiando; justo a cierto valor se genera la transición. Similarmente con el Higgs, tiene un potencial de auto interacción [3] cuyos parámetros cambian con la temperatura del Universo. En la transición de fase 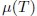cambia de signo, apareciendo la masa para los campos escalares o el Higgs en la ecuación de movimiento de esta partícula, conocida como la ecuación de Klein-Gordon.

Los metales como el hierro tienen un gas de muchos electrones los cuales se mueven aleatoriamente, dependiendo de la temperatura y su espín, 1/2. Para estudiar su comportamineto termodinámico es necesario definir una funcion de distribuci'on la cual, para partículas de espín 1/2 se conoce como la estadística de Fermi-Dirac. Cuando se comienzan a enfriar los electrones, los efectos de la red cristalina, los fonones o vibraciones mecánicas de la red, comienzan a correlacionarlos formando pares ligados de dos electrones con espínes en sentido contrario, creando un estado ligado de espín total igual a cero. A este nuevo estado se le conoce como el par de Cooper. Justo cuando comienza este proceso la resistencia eléctrica disminuye y los electrones pueden pasar cuasi libres a través del metal como si no existiera resistencia eléctrica y se mueven libremente sin generar calor [4].

Justo cuando hay suficiente número de electrones apareados en estados ligados, o pares de Cooper, el metal pasa al estado base, el cual se conoce como el estado superconductor. Estos pares son campos escalares los cuales requieren de una función estadística para poder estudiar su termodinámica o teoría de muchos cuerpos a una temperatura finita, la cual se conoce como la estad ística de Bose-Einstein. Los pares de Cooper son estados ligados, compuestos, formados por dos electrones correlacionados con espín total igual a cero. Los electrones libres en el metal pasan por los lados de los pares de Cooper sin interactuar con ellos y por esta razón se comportan como libres, es decir, sin experimentar resistencia eléctrica.

Cuando tratamos que un campo magnético penetre el metal, se inducen corrientes muy grandes impidiendo que los campos lo penetren. Podemos decir que los campos dentro del metal decaen muy rápidamente. En las ecuaciones de Maxwell aparece un término que se puede interpretar como si el campo magnético tuviera una masa efectiva, produciendo este rápido decaimiento de los campos electromagnéticos en la fase superconductora.

El par de Cooper en la fase superconductora se podría interpretar como un Higgs. Dota de masa al fotón en el medio material. La diferencia con el Higgs, que da masa a las partículas después de la transición de fase, es que el par de Cooper es compuesto, formado de dos electrones. El Higgs del Modelo Estándar de las interacciones electro-débiles es una partícula puntual y, sólo los experimentos de precisión en el LHC, nos indicarán si efectivamente el Higgs es una partícula elemental o es una partícula compuesta. En el segundo caso se abrirían nuevas fronteras inimaginables para la física de partículas.

Se podría afirmar que en la superconductividad hay una partícula que juega un papel similar al Higgs del Modelo Estándar. Justo de estos trabajos del estado sólido, el físico inglés Peter Higgs planteó la partícula Higgs. Cuando ocurre la transición de fase decimos que ocurrió un rompimiento espontaneo de la simetría, es decir, el Universo pasa de una fase donde todo se mueve con masa nula a otra fase donde las partículas se hacen masivas. Las partículas pasan de moverse a la velocidad de la luz, a una velocidad menor que la luz, dependiendo de su masa o de la forma como interactúa con el Higgs.

El rompimiento de la simetría hace que los campos mensajeros de la interacción débil W⁺,W^−,Z⁰ se hagan masivos. En cambio el fotón, mensajero de la electrodin ámica, no adquiere masa. Es decir, el campo de Higgs interactúa con los campos de la interacción débil, pero no con el fotón. El fotón puede pasar libremente a través del campo de Higgs y alcanzar los confines del Universo trayendo la luz de las estrellas y de las supernovas que explotaron millones de años atrás. En cambio los campos mensajeros de la interacción débil interactúan fuertemente con el campo de Higgs y no puede viajar una distancia mayor que la del núcleo atómico. Solo pude viajar una distancia pequeña y decirle a un quark vecino, dentro del protón o neutrón, que es portador de la interacción débil y al quark up que se transforme en quark down.

¿Por qué es tan importante el descubrimiento del Higgs?.

Hay varias razones para ver su importancia. El modelo estándar de las interacciones electro-débiles [5] explica muy bien estas fuerzas a nivel cuántico y además ha tenido muchos aciertos en sus predicciones. Por ejemplo, el descubrimiento del quark charm, el cual se postuló en la teoría para entender las corrientes neutras débiles. El descubrimiento del quark top, el cual se postuló en el Modelo estándar para completar el doblete de quarks entre el quark bottom y el quark top, necesario para que la teoría tuviera la estructura matemática correcta, es decir, libre de anomalías. Las corrientes cargadas en la interacción débil se conocian desde los años 1930 con el decaimiento del muón y el decaimiento del neutrón. A dichas corrientes cargadas se asociaba un campo cuántico llamado el campo de gauge W^±. La existencia de estos campos cuánticos requería la presencia de otro campo de carga eléctrica nula, el cual se llamó Z⁰. Estos fueron postulados para entender la teoría débil y posteriormente descubiertos en el laboratorio. Recientemente, la medición de la violación de la simetría CP en la oscilación sistema de mesones formados por estados ligados de un quark down y un quark extraño, es un éxito del Modelo Estándar porque dichos fenomenos habían sido postulados o predichos teóricamente y se requer ía de su observaci'on para darle un piso firme a la teoría. En el Modelo Estándar los neutrinos aparecían con masa cero. Sin embargo, no parecía natural que dichas partículas fueran de masa nula. Experimentos que detectaban neutrinos provenientes del Sol, se podían entender si se asumía que estos tenían masa diferente de cero. Igualmente se realizaban experimentos con neutrinos que provenían de la atmosfera en el decaimiento de los kaones.

En todo este concierto de predicciones teóricas y descubrimientos experimentales faltaba el campo de Higgs, el cual se introduce en la teoría para explicar cómo las partículas adquieren masa. Sin el Higgs, la teoría que fue capaz de predecir muchos fenómenos que fueron corroborados, nadie se esperaría que el mecanismo necesario para que el modelo fuera satisfactorio, se quedara sin piso. Descubierto el Higgs, se dá piso a la teoría y queda explicado el origen de la masa y la gravitación.

Partículas escalares de espín cero y carga elétrica cero, con caracteristicas similares a la Higgs descubierto en el LHC, se pueden relacionar con otro fenómeno muy importante que proviene de la cosmología. De las observaciones de la dinámica estelar, en particular estrellas girando alrededor de las galaxias, se ve que hay estrellas que se mueven mucho más rápido que la predicción que se puede hacer con la teoría de la gravitación de Newton. Al parecer hay mucho más materia en las galaxias para poder entender estas velocidades. A dicha materia se le llama materia oscura porque no se puede ver, pero está produciendo un fenómeno gravitacional, es decir, materia con masa pero sin carga electromagnética. También se ha observado galaxias acercándose por efecto gravitacional, pero al tener en cuenta la masa total de ellas, las predicciones no concuerdan con la teoría de gravitación de Newton. De nuevo se tiene que postular la existencia de materia oscura en el Universo. También existe un fenómeno conocido como lente gravitacional que hace que los rayos de luz que provienen de galaxias muy lejanas se curven y este sólo se puede explicar con la existencia de la materia oscura.

Se ha estimado la cantidad de galaxias y se dice que es sólo el 5% de la materia del Universo y, de la dinámica estelar, se dice que hay un 20% de materia oscura, es decir, hay más materia en el Universo que la que observamos contando todas las galaxias, cúmulos, estrellas etc. Podemos dar cuenta únicamente del 5% de la materia por observación directa del Universo. Por otra, el Universo tiene más energía de la que habíamos pensado. Con las observaciones recientes del satélite Hubble se han visto estrellas muchos más lejanas y distancias nunca antes imaginadas. Dichas estrellas se alejan tan rápido y aceleradamente, que con las teorías de Einstein de la gravitación, para poder explicar este fenómeno, necesitamos un 75% más de energía. A ésta se le llama energía oscura. La única partícula que podría ser candidata a materia oscura sería una partícula que tuviera características similares al bosón de Higgs descubierto recientemente en el CERN.

Por esto se abriría un nuevo campo de investigación en la física relacionado con la cosmología. Hasta la fecha no se había observado un bosón o partícula escalar con las características de un Higgs, campo escalar de espín cero y carga eléctrica nula. Una vez que se descubre el Higgs hay posibilidad de más Higgses en la naturaleza que tengan las características para ser candidatos a materia oscura. Entonces, estamos en la antesala para entender el origen del Universo y como funciona. Apenas sería el comienzo de una nueva era de investigación [6].

¿Qué sigue?

Identificado el Higgs con una masa cercana a 125 GeV, es decir, una masa similar a la de un átomo de uranio, entonces qué sigue. Una vez detectado el Higgs es necesario producirlo en el laboratorio en abundancia y comenzar a estudiar sus decaimientos para poder conocer sus propiedades y determinar si éste corresponde a un Higgs predicho por el modelo estándar de las interacciones electro-débiles o es un Higgs de una teoría más complicada. Sería el comienzo para establecer si hay más partículas de las ya descubiertas o sólo los quarks y leptones que ya identificamos en el laboratorio. La forma más sencilla de identificar un Higgs, aunque no la más probable, es cuando este decae en dos fotones .

Como el Higgs no tiene carga electromagnética, no puede interactuar con los fotones, pero se produce un fenómeno puramente cuántico, una fluctuación del vacío, donde se crean dos campos de interacción débil W⁺W^−, los cuales después decaen en los dos fotones. De esta forma se identificó el Higgs en el colisionador LHC [7]. Como todas las partículas masivas interactúan con el Higgs, este puede decaer en ellas. La probabilidad de decaimiento del Higgs depende de su masa. Para el bosón de Higgs del Modelo estándar con una masa de 125 GeV, como el descubieto en LHC, el modo más probable como puede decaer un Higgs es en dos quarks bottom, los cuales tienen una masa del orden de 5 GeV, es decir, cinco veces la masa de un protón o del orden de la masa del átomo de Helio; después decaer en dos gluones, dos leptones tau , dos quarks charm, etc. Sin embargo, el decaimiento en quarks es muy difícil de identificar en un colisionador hadrónico como el LHC porque a su vez los quarks decaen y las señales se pueden confundir con todos los productos de la colisión donde se ha liberado toda la energía que se inyectó en los protones iniciales. La identificación del Higgs decayendo en dos leptones tau también es difícil porque a su vez el tau decae en partículas más ligeras y neutrinos, los cuales no se pueden observar en los detectores como ATLAS y CMS [7]. Sin embargo, en la medida que se sintoniza la masa del Higgs y su forma de producirlo, se podrá mejorar la identificación de los otros canales. La probabilidad de decaimiento del Higgs en dos partículas es proporcional a la masa de las partículas finales, por eso entre más pesada la partícula más probable es el decaimiento del Higgs. El quark top tiene una masa mayor que la del Higgs y por esta razón no podría decaer en tops porque no se tendría la energía inicial necesaria para producir los tops. Decimos que este canal de decaimiento está prohibido cinemáticamente. También sería muy importante estudiar como interactúa el Higgs consigo mismo debido a que nos revela sus propiedades y como adquirió masa. También nos daría información de cómo funciona el famoso rompimiento de la simetría que justo dio origen al Higgs.

5. Conclusión

El descubrimiento del Higgs establece que el mecanismo para generar las masas de las partículas es el correcto y el Modelo Estándar de las interacciones electrodébiles es una teoría bien formulada. Por otra parte se abre un nuevo horizonte de investigación y la pregunta es existen más partículas en otra escala del Universo o la historia de cierra con la gran explosión y, hasta la escala de Planck, sólo hay un gran desierto. ¿Existen la supersimetría, nuevos campos de Higgs, más fermiones, dimensiones extras, nuevas corrientes neutras? ¿Es un campo de Higgs, singlete del Modelo Estándar, el candidato a materia oscura? [8]

Agradecimientos. A COLCIENCIAS.

Referencias

[1] John D. Anderson. Fundamentals of Aerodynamics. McGraw-Hill;         [ Links ] Pijush K. Kundu, Ira M. Cohen, Howard H. Hu. Fluid Mechanics. Elsevier/Academic Press.         [ Links ]

[2] Peter Higgs. Broken Symmetries and the Masses of Gauge Bosons. Physical Review Letters 13, 508 (1964);         [ Links ] Francois Englert & Robert Brout. Broken Symmetry and the Mass of Gauge Vector Mesons. Physical Review Letters 13, 321 (1964);         [ Links ] Gerald Guralnik; C. R. Hagen & Kibble, T. W. B. Global Conservation Laws and Massless Particles. Physical Review Letters 13, 585 (1964)        [ Links ]

[3] L. Ginzburg & L. D. Landau. On the theory of superconductivity. Zhurnal Eksperimental'noi i Teoreticheskoi Fiziki 20, 1064, (1950).         [ Links ] Peter Higgs. Spontaneous Symmetry Breakdown without Massless Bosons. Physical Review 14, 1156 (1966).         [ Links ]

[4] J. Bardeen, L. N. Cooper & J. R. Schrieffer. Theory of Superconductivity. Physical Review 108, 1175 (1957)        [ Links ]

[5] L. Glashow. Partial-symmetries of weak interactions. Nuclear Physics 22, 579 (1961);         [ Links ] S. Weinberg. A Model of Leptons. Physical Review Letters 19, 1264 (1967);         [ Links ] A. Salam. N. Svartholm, ed. Elementary Particle Physics: Relativistic Groups and Analyticity. Eighth Nobel Symposium. Stockholm: Almquvist and Wiksell. pp. 367 (1968).         [ Links ]

[6] S. Weinberg. Cosmology. Cambridge Academic Press;         [ Links ] E. W. Kold & M. S. Turner. The Early Universe. Addison- Wesley;         [ Links ] J. V. Narlikar. An Introduction to Cosmology. Cambridge Academic Press.         [ Links ]

[7] ATLAS Collaboration. Combined search for the Standard Model Higgs boson in pp collisions at sqrt(s) = 7 TeV with the ATLAS detector. arXiv:1207.0319 [hep-ex]         [ Links ]; The CMS Collaboration. Observation of a new boson at a mass of 125 GeV with the CMS experiment at the LHC. arXiv:1207.7235 [hepex]         [ Links ]

[8] A. Drozd, B. Grzadkowski, Jose Wudka. Multi-Scalar- Singlet Extension of the Standard Model - the Case for Dark Matter and an Invisible Higgs Boson. JHEP 1204, 006 (2012);         [ Links ] Alexander Kusenko. Sterile neutrinos, dark matter, and the pulsar velocities in models with a Higgs singlet. Physical Review Letter 97, 241301 (2006);         [ Links ] M. S. Boucenna, S. Profumo. Direct and Indirect Singlet Scalar Dark Matter Detection in the Lepton-Specific two-Higgs-doublet Model. Physical Review D84, 055011 (2011);         [ Links ] John McDonald. Gauge singlet scalars as cold dark matter. Physical Review D50, 3637 (1994).         [ Links ]

Recibido el 5 de junio de 2012

Aceptado para su publicación el 12 de junio de 2012