doi: http://dx.doi.org/10.18257/raccefyn.308

¹ Grupo de Investigación Insight, Línea de Profundización e Internado Especial Teorías físicas y matemáticas aplicadas a la Medicina, Universidad Militar Nueva Granada. Bogotá, D.C., Colombia *Correspondencia: Javier Rodríguez Velásquez, grupoinsight2025@yahoo.es
² Centro de Investigaciones de la Clínica del Country, Bogotá, D.C., Colombia
³ Facultad de Medicina, Universidad Militar Nueva Granada, Bogotá, D.C., Colombia
⁴ Departamento de Matemáticas, Universidad Militar Nueva Granada, Bogotá, D.C., Colombia

Recibido: 7 de noviembre de 2015. Aceptado: 3 de mayo de 2016

Resumen

La teoría de sistemas dinámicos, así como la probabilidad y las proporciones de la entropía, sustentan una nueva metodología diagnóstica predictiva que diferencia los estados normales, agudos y crónicos, y la progresión hacia la enfermedad. En este estudio se evaluó la probabilidad y la entropía y sus proporciones de atractores dinámicos construidos a partir de la frecuencia cardiaca y el número de latidos por hora de 30 registros en monitor Holter normales y 60 de infarto agudo de miocardio. La metodología diferenció las dinámicas indicativas de infarto agudo de miocardio de aquellas normales, y cuantificó su nivel de gravedad, lo que la convierte en una herramienta de diagnóstico útil en la práctica clínica.

Palabras clave: diagnóstico, infarto agudo de miocardio, cuidado crítico.

Abstract

The theory of dynamical systems, as well as probability and entropy proportions support a predictive diagnostic methodology which differentiates normal, acute and chronic states and progression towards disease.We evaluated probability and entropy and its proportions of attractors constructed from heart rate and number of beats per hour of 30 normal Holter records and 60 with acute myocardial infarction. The methodology differentiated those dynamics indicative of myocardial infarction from normal ones, and quantified the severity of the dynamics, which makes it a useful diagnostic tool in clinical practice.

Key words: Diagnosis, acute myocardial infarction, critical care.

Introducción

La teoría de los sistemas dinámicos tiene como objeto de estudio el estado y la evolución de los sistemas (Devaney, 1992). En el contexto de esta teoría la dinámica puede representarse en espacios de fase y constituir atractores que pueden ser predecibles o impredecibles; un ejemplo de estos últimos son los atractores caóticos, como los que se observan en la dinámica cardiaca. Estos atractores presentan una forma irregular, la cual puede medirse mediante la geometría fractal (Peitgen, et al., 1992). Otra de las teorías usadas en el análisis de los sistemas es la teoría de la probabilidad; la probabilidad es una medida de la posibilidad de que un evento ocurra en el futuro en un espacio muestral determinado desde el cual se define una función matemática que cuantifica todas las probabilidades (Mood, et al., 1974; Laplace, 1995). En este trabajo no se hizo uso de la probabilidad como medida estadística sino como medida predictiva en el contexto de la entropía, la cual se definió inicialmente en el marco de la teoría cinética de los gases como una función del número de posibles estados para sistemas equiprobables, y posteriormente se generalizó en la mecánica estadística para los sistemas no equiprobables (Matvéev, 1987; Tolman, 1979), y se ha reinterpretado en diferentes campos como sucede en la teoría de la información (Machta, 1999).

Según los reportes de la Organización Mundial de la Salud, enpara el 2011 las enfermedades cardiovasculares ocupaban el primer lugar en cuanto a mortalidad a nivel mundial, con 30 % de las muertes reportadas. Entre todas las enfermedades cardiovasculares, la cardiopatía isquémica representaba 42 % de las causas de muerte. En Colombia el infarto agudo de miocardio se encontraba entre las primeras cinco causas de mortalidad según los reportes del Departamento Administrativo Nacional de Estadística (DANE) para el 2009, conpn 28.650 muertes (Robledo & Escobar, 2010).

Diversas investigaciones en el campo de la cardiología y la medicina intensiva se han enfocado al estudio de la variabilidad de la frecuencia cardiaca a partir de los cambios en el intervalo RR (Malik, 1996; Chen,, 2008; Chen & Kuo, 2007; Huikuri, et al., 2000; Mäkikallio, et al., 2001; Voss, et al., 2009), sin embargo, su aplicabilidad clínica es limitada, y no ha sido posible establecer medidas predictivas generalizadas a partir de su análisis. El análisis de la variabilidad se basa en la concepción homeostática convencional que equipara la normalidad con un comportamiento cardiovascular regular; no obstante, se ha evidenciado que la dinámica cardiaca exhibe un comportamiento irregular, con características no lineales como las del comportamiento caótico (Wu, et al., 2009; Braun, et al., 1998). En el marco de la teoría de los sistemas dinámicos, Goldberger, et al. (2002) han propuesto una reinterpretación de la concepción de normalidad y enfermedad aplicada a la fisiología cardiaca que contradice la concepción homeostática convencional, en la cual se evidencia que tanto el comportamiento regular y periódico como un comportamiento excesivamente aleatorio se consideran patológicos, en tanto que el estado de normalidad se halla en medio de estos dos comportamientos extremos. Los análisis desarrollados a partir de la teoría de los sistemas dinámicos y de la geometría fractal han resultado ser predictores de la mortalidad más eficaces que los convencionales en pacientes con infarto agudo de miocardio con fracción de eyección menor a 35 % (Huikuri, et al., 2000); del mismo modo, se han desarrollado métodos predictivos de la muerte en pacientes con falla cardiaca (Mäkikallio, et al., 2001) y en pacientes con sepsis (Chen, et al., 2008; Chen & Kuo, 2007; Gómez, et al., 2012).

Desde esta perspectiva, Rodríguez (2010a) desarrolló un método de evaluación de la dinámica cardiaca a partir de los registros continuos en monitor Holter en pacientes mayores de 21 años mediante una inducción matemática que permitió diferenciar los estados de normalidad, de enfermedad crónica y aguda, y de la evolución entre estos estados. Dicha metodología se basó en la evaluación de la ocupación de pares ordenados de la frecuencia cardiaca entre los atractores de diez pacientes en un espacio de fases, utilizando la teoría de los sistemas dinámicos, la teoría de la probabilidad y las proporciones de la entropía, lo cual permitió el establecimiento de medidas diagnósticas preventivas cuya aplicabilidad clínica se ha podido confirmar (Rodríguez, 2011; Rodríguez, 2012a; Rodríguez, et al., 2013; Rodríguez, et al., 2014; Rodríguez, et al., 2015).

Además, esta metodología se ha aplicado a la predicción de la dinámica cardiaca en la unidad de cuidados coronarios, en donde se logró establecer cuantitativamente que después de la intervención quirúrgica de un paciente que no evidenciaba deterioro clínico, sus proporciones de la entropía mostraban una agudización de la dinámica cardiaca, lo cual se corroboró clínicamente más tarde (Rodríguez, et al., 2015). Así mismo, el método se aplicó a la evaluación de casos normales y otros de pacientes de la unidad de cuidados coronarios, y se logró predecir exitosamente tanto la normalidad como la enfermedad aguda y crónica. También fue posible cuantificar el impacto que tenían las intervenciones quirúrgicas o farmacológicas sobre la dinámica cardiaca mediante el cambio en las proporciones geométricas del atractor caótico (Rodríguez, 2011).

En este contexto, el propósito del presente trabajo fue confirmar la aplicabilidad clínica de la metodología previamente desarrollada (Rodríguez, 2010a), contrastando el diagnóstico físico-matemático con el diagnóstico clínico convencional de dinámicas cardiacas normales y de las de pacientes con infarto agudo de miocardio atendidos en la unidad de cuidados intensivos.

Materiales y métodos

Definiciones

Espacio de fases: espacio de dos o más dimensiones en el que se representa de manera gráfica la dinámica de un sistema por medio de la representación geométrica de sus variables en un tipo de atractor específico en el cual se ubican pares ordenados de los valores de cada variable consecutiva en el tiempo.

Par ordenado de variables dinámicas: corresponde a la combinación de dos frecuencias cardiacas consecutivas en el espacio de fases representadas como (x,y) y distribuidas en rangos de cinco según sus coordenadas.

Probabilidad de pares ordenados: corresponde al cociente que resulta de dividir el número de pares ordenados que ocupan un rango específico de cinco en entre el número total de pares ordenados de todo el registro Holter (Rodríguez, 2010a). Se representa mediante la siguiente ecuación, en la cual X y Y son múltiplos de 5:

Entropía del atractor: la entropía de la ocupación de un atractor en el espacio de fases se calcula mediante la ecuación de la entropía no equiprobable de Boltzmann-Gibbs:

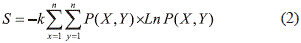
donde X, Y son múltiplos de 5; P (X,Y) corresponde a la probabilidad para el rango (X,Y), k representa la constante de Boltzmann, cuyo valor es 1,38x10^-23 (joules/kelvin), y S representa la entropía (Matvéev, 1987; Tolman, 1979).

Proporción S/k del atractor: se obtiene de la ecuación 2 al dividirla por la constante de Boltzmann:

la cual puede rescribirse así:

donde a, b, c, d, e, f, g, h representan los múltiplos de la frecuencia cardiaca en múltiplos de 5, P (a,b) es igual al valor de la probabilidad para los rangos con frecuencias de ocupación del orden de unidades, P (c,d) es igual al valor de la probabilidad para los rangos con frecuencias de ocupación del orden de decenas, P (e,f) es igual al valor de la probabilidad para los rangos con frecuencias de ocupación del orden de centenas, P (g,h) es igual al valor de la probabilidad para los rangos con frecuencias de ocupación del orden de miles, K representa la constante de Boltzmann, 1,38x10^-23 (joules/kelvin), y S es el valor de la entropía (Matvéev, 1987; Tolman, 1979).

La ecuación anterior, se puede simplificar como sigue:

donde U corresponde a la suma de las probabilidades asociadas a frecuencias de ocupación del orden de unidades por su logaritmo natural, D corresponde a estos mismos valores para el orden de decenas, C a los de centenas, y M a los de miles, mientras que k es igual a la constante de Boltzmann, 1,38x10^-23 (joules/kelvin), y S es el valor de la entropía.

Proporciones de la entropía: corresponden a las divisiones entre las sumas previamente definidas con respecto a la totalidad (T), que a su vez corresponde a la proporción S/k, o a ellas mismas:

Regiones del atractor: regiones definidas con base en los prototipos de la inducción de la siguiente manera.

La región uno, que abarca todos los rangos de la frecuencia cardiaca comunes a los registros en monitor Holter normales.

La región dos, que incluye todos los rangos ocupados por los registros en monitor Holter normales, excluidos los de la región uno.

La región tres, que comprende los rangos de frecuencia cardiaca de la región total restante del espacio de fases correspondiente a los que no son ocupados por los prototipos normales.

Procedimiento

Se analizaron 90 registros continuos de la frecuencia cardiaca producto de la monitorización con monitor Holter durante 21 horas. Treinta de estos registros correspondían a pacientes con diagnósticos normales y 60 a pacientes con infarto agudo de miocardio cuyos registros provenían de la base de datos del Grupo Insight. La conclusión sobre el diagnóstico basado en el registro en monitor Holter fue emitida por un cardiólogo experto según los parámetros convencionales, y se enmascaró para garantizar un estudio ciego, dejando visibles solamente los valores de las frecuencias cardiacas mínima y máxima cada hora, así como el número de latidos por hora.

A partir de estos valores máximos y mínimos de la frecuencia cardiaca se realizó una simulación computacional de la totalidad del trazado electrocardiográfico con el fin de construir el atractor cardiaco en el espacio de fases según la metodología previamente desarrollada (Rodríguez, et al., 2014; Rodríguez, 2010a; Rodríguez, et al., 2013; Rodríguez, 2011; Rodríguez, 2012; Rodríguez, et al., 2015), graficando la frecuencia de aparición de cada uno de los pares ordenados agrupados en rangos de múltiplos de cinco latidos por minuto. A continuación se evaluó la probabilidad de ocupación para cada uno de los rangos y cada una de las regiones, asumiendo que cada pareja de frecuencias cardiacas constituía un evento (ecuación 1). Se procedió a hallar la entropía de cada atractor (ecuación 2) y la relación S/k (ecuación 3).

Los sumandos que correspondían a las probabilidades de frecuencias de ocupación del orden de unidades (1-9) se agruparon y se sumaron (ecuación 4), al igual que los de decenas (10-99), centenas (100-999) y miles (1.000 a 9.999). Estos valores fueron consecutivamente utilizados para calcular las proporciones existentes entre cada sumando con respecto a la totalidad (relación S/k) y entre las partes (centenas/miles y centenas/decenas), las cuales se calcularon para cada región determinada (ver definiciones).

Más adelante, se evaluó si por lo menos dos de las pro-porciones en cualquiera de las tres regiones se encontraban por fuera de los límites de la normalidad definidos previamente (Rodríguez, 2010a), asumiendo esta condición como diferenciadora entre normalidad y enfermedad. Para establecer cuantitativamente el nivel de gravedad de cada dinámica con respecto a los límites de normalidad, se restó de los valores de las proporciones mayores que el límite superior de normalidad este último valor, mientras que los valores menores que el límite inferior de normalidad se restaron de este valor límite. Dichas diferencias se agruparon en cuatro conjuntos de acuerdo a si estaban asociadas con frecuencias del orden de los miles, las centenas, las decenas o las unidades, mediante una suma aritmética de cada grupo, lo cual permitió cuantificar qué tan lejos se encontraban estas proporciones de la normalidad, pues entre mayores sean estos valores, más alejada de la normalidad se considera la dinámica. Los valores de la suma de las restas del orden de los miles son las que tienen mayor peso en la determinación del nivel de gravedad de la dinámica, después se evalúan consecutivamente los valores de las centenas, decenas y unidades. El aumento de las sumas del orden de los miles corresponde a una agudización o deterioro de la condición de un paciente, lo cual puedese manifiestarse clínicamente como un infarto agudo de miocardio, por ejemplo (Rodríguez, et al., 2015). En el caso de que las sumas del orden de miles tiendan a disminuir consecutivamente en el tiempo, esto indicaría una evolución a un estado menos agudo.

Análisis estadístico

Para confirmar la aplicabilidad clínica del diagnóstico físico-matemático, se comparó el diagnóstico convencional, el cual se asumió como el estándar, con el resultado arrojado por la metodología matemática, calculando la especificidad y la sensibilidad. Para obtener estos valores, se hizo una clasificación binaria en la que los verdaderos positivos correspondían al número de pacientes con diagnóstico convencional y físico-matemático de la enfermedad; los falsos positivos, al número de casos diagnosticados matemáticamente como patológicos, pero cuyo diagnóstico convencional era normal; los falsos negativos, al número de casos diagnosticados matemáticamente como normales, pero cuyo diagnóstico convencional era patológico, y los verdaderos negativos correspondían a aquellos casos con diagnóstico de normalidad tanto desde el punto de vista matemático como clínico.

Para evaluar la concordancia entre los dos diagnósticos, se calculó el coeficiente kappa mediante la siguiente ecuación:

donde Co corresponde al número de concordancias observadas, en otras palabras, el número de pacientes con el mismo diagnóstico matemático y estándar; To corresponde a la totalidad de observaciones, es decir, la totalidad de casos normales y patológicos, y Ca corresponde a las concordancias atribuibles al azar, las cuales se calculan de acuerdo con la siguiente fórmula:

donde f1 representa el número de pacientes con valores matemáticos de normalidad, C1 representa el número de pacientes diagnosticados clínicamente como normales, f2, el número de pacientes con valores matemáticos indicativos de enfermedad, C2, el número de pacientes diagnosticados clínicamente como patológicos y To, el número total de casos normales y patológicos.

Resultados

Al evaluar los registros del monitor Holter de los pacientes con infarto agudo de miocardio, los valores de la entropía variaron entre 4,6062X10^-23 y 5,069X10^-23. En los registros normales, este valor se halló entre 6,478X10^-23 y 7,058X10^-23 (tabla 1). Se encontró que para los registros de los pacientes con infarto agudo de miocardio, los valores de la relación S/k variaron entre -3,6733 y -3,3378. En el caso de los registros normales, los valores de la relación S/k se encontraron entre -5,115 y -4,694 (tablas 1 y 2). Se evidenció que tanto las medidas de entropía como las relaciones S/k diferenciaron cuantitativamente los grupos.

En de los pacientes con infarto agudo de miocardio, los valores de las proporciones de la entropía U/T se encontraron entre 0 y 0,0020, los de la entropía D/T estuvieron entre 0,0077 y 0,0480, los de C/T, entre 0,0684 y 0,3974, los de M/T variaron entre 0,5753 y 0,8784, los de C/M entre 0,0778 y 0,6908 y los de D/C entre 0,0310 y 0,2337. En los registros normales los valores de la proporción U/T de la entropía se encontraron entre 0 y 0,0084, los de D/T entre 0 y 0,1345, los de C/T entre 0 y 0,5515, los de M/T entre 0 y 0,4592, los de C/M entre 0 y 3,5131 y los de D/C entre 0 y 3,2814. Ninguno de los casos normales presentó valores correspondientes a las sumas de las restas de las proporciones de la entropía por fuera de los límites de normalidad, mientras que en los pacientes con infarto agudo de miocardio se encontraron por lo menos dos valores por fuera de estos límites. Además, las medidas matemáticas de las sumas de las restas de las proporciones por fuera de los límites de normalidad del orden de los miles se encontraron entre 0,4194 y 2,2593, y las del orden de las centenas, entre 0,1348 y 3,3521 (tablas 1 y 2), lo cual evidenció el carácter agudo de las dinámicas indicativas de infarto agudo de miocardio.

Los valores de sensibilidad y especificidad encontrados para esta metodología fueron de 100 %, con un coeficiente kappa de 1, lo cual confirma la capacidad de la metodología para diferenciar clínicamente las dinámicas cardiacas normales de aquellas indicativas de infarto agudo de miocardio.

Asimismo, al desenmascarar los datos se observó que había tres registros de un mismo paciente en tres días consecutivos, en cuyo caso se observó que las sumas del orden de los miles habían permanecido relativamente estables entre el día 1 y el día 2, con valores de 1,2001 y 1,1101, respectivamente (registros 10.1 y 10.2 de la tabla 2). Sin embargo, pasaron de 1,1101 a 2,2593 en el día 3 (registros 10.2 y 10.3 de la tabla 2); de igual forma, las sumas de las centenas pasaron de 0,3217 a 2,7122. Las diferencias en los valores de las sumas de las centenas y de los miles evidenciaron cuantitativamente la evolución progresiva de la dinámica hacia un estado mucho más crítico. Esta evolución hacia la agudización se corroboró con los datos clínicos del paciente y el diagnóstico emitido por el especialista.

Discusión

Este el primer trabajo en el que se establece la capacidad de la metodología diagnóstica basada en la teoría de la probabilidad y la entropía proporcional del atractor cardiaco para diferenciar clínicamente dinámicas normales de aquellas indicativas de infarto agudo de miocardio en pacientes atendidos en la unidad de cuidados intensivos y en el contexto de un estudio ciego de concordancia diagnóstica. Los resultados de este estudio indican que la dinámica cardíaca de todos los pacientes con infarto agudo de miocardio presentó valores matemáticos característicos de la enfermedad aguda, que permitieron su diferenciación de los estados de normalidad. Al comparar los diagnósticos clínicos con los resultados encontrados mediante un aná-lisis estadístico, se obtuvieron los máximos valores de sensibilidad y especificidad, y de coeficiente kappa, lo cual confirma la aplicabilidad clínica de esta metodología.

Así mismo, la metodología previamente desarrollada permitió cuantificar el grado de gravedad del compromiso cardiaco a partir de la distancia de las proporciones de la entropía con respecto a los límites de normalidad y la agudización de una dinámica particular de un día a otro. El registro de la evolución estudiado en los registros 10.1, 10.2 y 10.3, provenientes del mismo paciente en tres días consecutivos, mostró diferencias significativas en la transición de un paciente con infarto agudo de miocardio hacia un estado más agudo, evidenciando la capacidad de la metodología para cuantificar procesos que evolucionan hacia la agudización o "estabilización". De este modo se demostró que la metodología diagnóstica puede facilitar la evaluación oportuna de intervenciones farmacológicas y quirúrgicas, por lo cual constituye una herramienta de apoyo en las decisiones terapéuticas en la unidad de cuidados intensivos y en otros contextos, y confirma los hallazgos previos (Rodríguez, et al., 2014; Rodríguez, et al., 2013; Rodríguez, 2011; Rodríguez, 2012, Rodríguez, et al., 2015).

En otros estudios las metodologías desarrolladas para la evaluación de la dinámica cardiaca se han enfocado en el análisis de la variabilidad mediante la medición de la magnitud global de la fluctuación RR alrededor de su valor medio, o de la magnitud de las fluctuaciones de algunas frecuencias predeterminadas. Por el otro lado, debido al comportamiento impredecible de la dinámica cardiaca, se han desarrollado múltiples métodos de evaluación a partir de la teoría del caos y la teoría de los sistemas no lineales (Schumacher, 2004; Babloyantz & Destexhe, 1988), entre los cuales se encuentran los de la medición de la entropía aproximada (Pincus, 1991; Richman & Moorman, 2000), el análisis multifractal (Ivanov, et al., 1999), y la entropía muestralsample (Richman & Moorman, 2000), entre otros. Sin embargo, sus alcances se limitan a enfermedades específicas y requieren de validaciones adicionales para su aplicabilidad clínica (Voss, et al.,2009; Richman & Moorman, 2000). Los valores obtenidos al comparar el diagnóstico convencional con esta metodología físico-matemática mediante el análisis estadístico fueron de 100 % para la sensibilidad y la especificidad, lo cual pone de manifiesto su utilidad como herramienta de ayuda diagnóstica en la clínica.

En el campo de la teoría de los sistemas dinámicos aplicada a la dinámica cardiaca, se desarrolló una ley exponencial para predecir la evolución hacia la agudización del comportamiento cardiaco (Rodríguez, 2011a), cuya aplicabilidad fue confirmada posteriormente en el marco de un estudio ciego con 115 registros en monitor Holter normales e indicativos de enfermedad, con valores de sensibilidad y especificidad de 100 % y un coeficiente kappa de uno (Rodríguez, et al., 2013a), lo cual que también la convierte en una herramienta de prevención aplicable a la clínica. Recientemente se realizó un estudio con la misma metodología aplicada a pacientes con arritmias cardiacas, el cual reveló su aplicabilidad general al evaluar y detectar ligeros cambios de la dinámica que no se habían determinado clínicamente como patológicos (Rodríguez, et al., 2013b).

Uno de los inconvenientes que tienen las metodologías de diagnóstico actuales es que al estar basadas en consideraciones estadísticas, sus afirmaciones se aplican a grupos poblacionales, pero no pueden hacer predicciones en cuanto a los individuos. En cambio la metodología aplicada en este trabajo está sustentada en las formas de razonamiento no causal de la física moderna. Así, del mismo modo que en la mecánica cuántica (Feynman, 1964a), la mecánica estadística (Feynman, et al., 1964b; Tolman, 1979), o la teoría del caos (Geisel, 1982), es posible llegar a afirmaciones objetivas y reproducibles para cada caso particular, independientemente del análisis de carácter epidemiológico.

Se han desarrollado mecanismos de predicción en otros campos a partir de aproximaciones similares de la física y la matemática, por ejemplo, en la diferenciación de las células escamosas de cuello uterino normales y enfermas (Rodríguez, et al., 2010b), así como de eritrocitos normales y anormales (Correa, et al., 2012). También se desarrolló una generalización que halló todos los prototipos posibles de arteriales normales y con reestenosis posibles (Rodríguez, et al., 2010c), y en el campo de la salud pública, un método predictivo con una efectividad de 99,86 % (Rodríguez, 2010d). Recientemente, se hizo una predicción con aplicabilidad clínica relativa a los linfocitos T CD4 a partir de la información del cuadro hemático en pacientes con VIH (Rodríguez, et al., 2012b; Rodríguez, et al., 2013c), y se han diseñado teorías para la predicción de la unión de péptidos al complejo mayor de histocompatibilidad de clase II (Rodríguez, 2008).

Conclusiones

Las proporciones de la entropía lograron diferenciar dinámicas cardiacas indicativas de infarto agudo de miocardio de aquellas normales. También se cuantificó qué tan alejada se encontraba la dinámica cardiaca de estos pacientes de la normalidad a partir de la cuantificación de su nivel de gravedad. El efecto de los agentes vasopresores e inotrópicos sobre la dinámica cardiaca requiere de un estudio más detallado que no se abordó en esta ocasión, de manera que se requieren nuevas investigaciones para hallar posibles asociaciones clínicas que permitan hacer predicciones de los resultados posteriores a las intervenciones médicas.

Agradecimientos

A los doctores Fernando Cantor, Vicerrector de Investigaciones, Martha Bahamón, Vicerrectora Académica, Jorge Enrique Luque, Decano de la Facultad de Medicina, Luis Antonio Castro, Director del Centro de Investigaciones, y al ingeniero Mario Alejandro Castro, Jefe de la División de Investigación Científica de la Universidad Militar Nueva Granada, así como al Centro de Investigaciones de la Clínica del Country, por su apoyo a nuestras investigaciones, específicamente a los doctores Tito Tulio Roa, Director de Educación Médica, Jorge Ospina, Director Médico, Alfonso Correa, Director del Centro de Investigaciones, y a las Doctoras Adriana Lizbeth Ortiz, epidemióloga, y Silvia Ortiz, Enfermera Jefe, de dicho Centro de Investigaciones.

Financiación

Producto derivado del proyecto MED-1345 financiado por la Vicerrectoría de Investigaciones de la Universidad Militar Nueva Granada - Vigencia 2014.

Conflicto de intereses

El autor declara no tener conflicto de intereses.

Bibliografía

Babloyantz, A. & Destexhe, A.(1988). Is the normal heart a periodic oscillator? Biol. Cybern. 58: 203-211.         [ Links ]

Braun, C., Kowallik, P., Freking, A., Hadeler, D., Kniffki, K., Meesmann, M. (1998). Demonstration of nonlinear components in heart rate variability of healthy persons. Am. J. Physiol. 275: H1577-H1584.         [ Links ]

Chen, W.L., Chen, J.H., Huang, C.C., Kuo, C.D., Huang, C.I., Lee, L.S. (2008). Heart rate variability measures as predictors of in-hospital mortality in ED patients with sepsis. Am J Emerg Med. 26 (4): 395-401.         [ Links ]

Chen, W.L. & Kuo, C.D. (2007). Characteristics of Heart Rate Variability Can Predict Impending Septic Shock in Emergency Department Patients with Sepsis. Acad EmergMed. 14 (5): 392-397.         [ Links ]

Correa, C., Rodríguez, J., Prieto, S., Álvarez, L., Ospino, B., Munévar, A., Bernal P., Mora, J., Vitery, S. (2012). Geometric diagnosis of erythrocyte. J. Med. Med. Sci. 3 (11): 715-720.         [ Links ]

Devaney, R. (1992). A first course in chaotic dynamical systems theory and experiments. Reading Addison-Wesley Reading: Massachusetts, p. 9-15.         [ Links ]

Feynman, R.P., Leighton, R.B., Sands, M. (1964a). Comportamiento cuántico. En: Feynman RP, Leighton RB, Sands M (ed). Física. Wilmington: Addison-Wesley Iberoamericana, S. A. p. 37-1- 37-16.         [ Links ]

Feynman, R.P., Leighton, R.B., Sands, M. (1964b). Leyes de la Termodinámica. Feynman RP, Leighton RB, Sands M (ed). Física. Wilmington: Addison-Wesley Iberoamericana S. A. p. 44-1-44-19.         [ Links ]

Geisel, T. (1982). Chaos, randomness and dimension. Nature. 298 (22): 322-323.         [ Links ]

Goldberger, A., Amaral, L., Hausdorff, JM., Ivanov, P., Peng, Ch., Stanley, HE. (2002). Fractal dynamics in physiology: Alterations with disease and aging. PNAS. 99: 2466- 2472.         [ Links ]

Gómez, M., Enciso, O., Peña, T., Segura, D., Nieto E. (2012). Estudio ECAIS: eventos cardiovasculares adversos inadvertidos en sepsis. Med Intensiva. 36 (5): 343-350.         [ Links ]

Huikuri, HV., Mäkikallio, T., Peng, C.K., Goldberger, A., Hintze, U., Møller, M. (2000). Fractal correlation properties of R-R interval dynamics and mortality in patients with depressed left ventricular function after an acute myocardial infarction. Circulation. 101: 47-53.         [ Links ]

Ivanov, P., Amaral, L., Goldberger, AL., Havlin, S., Rosenblum, M., Struzik, Z. (1999). Multifractality in human heartbeat dynamics. Nature. 399: 461-465.         [ Links ]

Laplace, P. (1995). Ensayo filosófico sobre las probabilidades. Barcelona: Altaya, p. 8-10, 12.         [ Links ]

Machta, J. (1999). Entropy, information, and computation. Am. J. Phys. 67: 1074-7.         [ Links ]

Mäkikallio, T.H., Huikuri, H.V., Hintze, U., Videbaek, J., Mitrani, R.D., Castellanos, A., Myerburg, R.J., Møller, M. (2001). Fractal analysis and time and frequency-domain measures of heart rate variability as predictors of mortality in patients with heart failure. Am. J. Cardiol. 87 (2):178-182.         [ Links ]

Malik, M. (1996). Heart rate variability: Standards of measurement, physiological interpretation, and clinical use. Circulation. 93: 1043-1065.         [ Links ]

Matvéev, A. (1987). Física molecular. Moscú: MIR, p.174-177.         [ Links ]

Mood, A., Graybill, F., Boes, D. (1974). Introduction to the theory of statistics. Singapore: Mc. Graw-Hill. p. 9-31         [ Links ]

Organización Mundial de la Salud. Enfermedades Cardiovasculares 2011. Disponible en: http://www.who.int/mediacentre/factsheets/fs317/es/index.html.         [ Links ]

Peitgen, H., Jurgens, H., Saupe, D. (1992). Strange attractors, the locus of chaos. Chaos and Fractals: New Frontiers of Science. New York: Springer-Verlag. p. 655-768.         [ Links ]

Pincus, S. (1991). Approximate entropy as a measure of system complexity. Proc. Natl Acad. Sci. USA. 88: 2297-2301.         [ Links ]

Richman, J., Moorman, J. (2000). Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 278: H2039-H2049.         [ Links ]

Robledo, R., Escobar, FA. (2010). Las enfermedades crónicas no transmisibles en Colombia. Boletín del Observatorio de Salud del Instituto Nacional de Salud. 3 (4): 1-9.         [ Links ]

Rodríguez, J. (2008). Teoría de unión al HLA clase II teorías de probabilidad combinatoria y entropía aplicadas a secuencias peptídicas. Inmunología. 27 (4): 151-66.         [ Links ]

Rodríguez, J. (2010a). Entropía proporcional de los sistemas dinámicos cardiacos: predicciones físicas y matemáticas de la dinámica cardiaca de aplicación clínica. Rev Colomb Cardiol. 17: 115-129.         [ Links ]

Rodríguez, J., Prieto, S., Correa, C., Posso, H., Bernal, P., Puerta, G., Vitery S., Rojas, I. (2010b). Generalización fractal de células preneoplásicas y cancerígenas del epitelio escamoso cervical: una nueva metodología de aplicación clínica. Rev Fac Med. 18 (2): 33-41.         [ Links ]

Rodríguez, J., Prieto, S., Correa, C., Bernal, P., Puerta, G., Vitery, S., Soracipa, Y., Muñoz, D. (2010c). Theoretical generalization of normal and sick coronary arteries with fractal dimensions and the arterial intrinsic mathematical harmony. BMC Medical Physics. 10 (1):1-3         [ Links ]

Rodríguez, J. (2010d). Método para la predicción de la dinámica temporal de la malaria en los municipios de Colombia. Rev Panam Salud Pública. 27: 211-8.         [ Links ]

Rodríguez, J. (2011). 7th International Meeting of Intensive Cardiac Care, Israel Heart Society, European Society of Cardiology, EBAC. Tel Aviv (Israel).         [ Links ]

Rodríguez, J. (2011a). Mathematical law of chaotic cardiac dynamics: Predictions for clinical application. J Med Med Sci. 2 (8): 1050-1059.         [ Links ]

Rodríguez, J. (2012a). Proportional Entropy applied to the Clinic Prediction of Cardiac Dynamics. Innovations in Cardiovascular Interventions, ICI meeting, Tel-Aviv (Israel).         [ Links ]

Rodríguez, J., Prieto, S., Bernal, P., Pérez, C., Correa, C., Álvarez, L., Bravo, J., Perdomo, N., Faccini, A. (2012b). Predicción de la concentración de linfocitos T CD4 en sangre periférica con base en la teoría de la probabilidad. Aplicación clínica en poblaciones de leucocitos, linfocitos y CD4 de pacientes con VIH. Infectio. 16 (1): 15-22.         [ Links ]

Rodríguez, J., Prieto, S., Domínguez, D., Melo, M., Mendoza, F., Correa, C., Soracipa, Y., Pinilla, L., Pardo, J., Ramírez, N. (2013). Mathematical-physical prediction of cardiac dynamics using the proportional entropy of dynamic systems. J Med Med Sci. 4 (8): 370-381.         [ Links ]

Rodríguez, J., Correa, C., Melo, M., Domínguez, D., Prieto, S., Cardona, DM., Soracipa, Y., Mora, J. (2013a). Chaotic cardiac law: Developing predictions of clinical application. J Med Med Sci. 4 (2): 79-84.         [ Links ]

Rodríguez, J., Narváez, R., Prieto, S., Correa, C., Bernal, P., Aguirre, G., Soracipa, Y., Mora, J. (2013b). The mathematical law of chaotic dynamics applied to cardiac arrhythmias. J Med Med Sci. 4 (7): 291-300.         [ Links ]

Rodríguez, J., Prieto, S., Correa, C., Pérez, C., Mora, J., Bravo, J., Soracipa, Y., Álvarez, L. (2013c). Predictions of CD4 lymphocytes' count in HIV patients from complete blood count. BMC Medical Physics. 13 (3): 1-3.         [ Links ]

Rodríguez, J., Prieto, S., Correa, C., Soracipa, Y., Aguirre, G., Méndez, L. (2014). Proportional entropy applied to the clinical diagnostic of cardiac dynamic: bBlind study with 600 holter. International Conference of the Israel Heart Society in association with The Israel Society of Cardiothoracic Surgery. April 30-May 1; Tel Aviv (Israel).         [ Links ]

Rodríguez, J., Prieto, S., Bernal, P., Izasa, D., Salazar, G., Correa, C., Soracipa, Y. (2015). Entropía proporcional aplicada a la evolución de la dinámica cardiaca. Predicciones de aplicación clínica. La emergencia de los enfoques de la complejidad en América Latina. Tomo I. Argentina: Comunidad del pensamiento complejo. p. 247-264.         [ Links ]

Schumacher, A. (2004). Linear and nonlinear approaches to the analysis of R-R interval variability. Biol Res Nurs. 5: 211-221.         [ Links ]

Tolman, R. (1979). Principles of statistical mechanics. New York: Dover Publications, p.565-571.         [ Links ]

Voss, A., Schulz, S., Schroeder, R., Baumert, M., Caminal P. (2009). Methods derived from nonlinear dynamics for analysing heart rate variability. Phil. Trans. R. Soc. A. 367 (1887): 277-296.         [ Links ]

Wu, G.Q., Arzeno, N.M., Shen, L.L., Tang, D.K., Zheng, D.A., Zhao, N.Q., Eckberg, D.L., Poon, C.S. (2009). Chaotic Signatures of Heart Rate Variability and Its Power Spectrum in Health, Aging and Heart Failure. PLoSOne. 4 (2): 4323.         [ Links ]