Introduction
The main purpose of Photogrammetry is to reconstruct a three-dimensional space, known as the object-space, based on two-dimensional images, corresponding to the image-space. Starting out from this perspective, digital photogrammetry reconstructs the mapped images in a semi-automated manner; in other words, with the least possible human manual intervention within this process (Coelho and Brito, 2007). In addition, as Koken et al. report (2014), photogrammetry has become the preferred tool for some new disciplines, thanks to the progress that has been made in image processing. Therefore, it is also important to mention the different applications in a wide range of different areas, particularly and specifically regarding digital close-range photogrammetry. In areas such as dentistry and orthodontics, as shown through the example shown in Fu et al. (2017). In the transport area, considering the best urban route bearing snow deposits in mind (Basnet et al., 2016). In the reconstruction of historical heritage buildings and sites, which is the subject of interest in this paper, and which has also been mentioned in the study by Cârlan and Dovleac (2017). In sports, as mentioned by Colorado and Santos (2015), where they show the development of a low-cost hardware/software system based on close range photogrammetry to track the movement of a person performing weightlifting. Other more specific studies aimed at calibration of cameras used in digital close-range photogrammetry applications, as mentioned by Long et al. (2017). It will be important, in addition, to read the studies developed by Cedeño-Valdiviezo and Torres-Lima (2019), Gutiérrez-Morales (2020), Santofimio-Ortiz and Pérez-Agudelo (2020), Ayala-García (2021), Llanos-Chaparro et al (2022), Cortés-Garzón (2023), among others.
Considering the state of the art in close range applications there are some recent works, such as those by Bill et al. (2022), Ferencík et al. (2022), Gnann et al. (2022), Illmann et al. (2022), Lauria et al. (2022), Maric et al. (2022), Murtiyoso et al. (2022), Nategh et al. (2022), Paixão et al. (2022), Petruccioli et al. (2022).
The main purpose of Topography is to present a detailed report on part of the Earth's surface, using numerous positioning techniques, through measurements to acquire information that will be the basis for this representation; in other words, the three-dimensional coordinates of specific points (Gonçalves et al., 2012). In this context, the technical conditions of the equipment used, in terms of precision and accuracy, must also be considered.
This issue is addressed in the technical standards published by the Brazilian Association of Technical Standards - ABNT (NBR 13133/2021) (ABNT, 2021), as well as in the German technical standards DIN 8723-1 (DIN, 1990a) and DIN 8323-2 (DIN, 1990b), GIAA (2002), which have been discussed by many different authors and have been taken into consideration in their respective research studies and applications, such as in Paciléo Netto (1993, 1997), Faggion (2001), Brun (2005), Silva (2008), Silva et al (2010), Cintra and Rocco (2014), among others.
Spatial Geodesy techniques, particularly the GNSS (Global Navigation Satellite System), allow the three-dimensional establishment of points, with their position, speed, and time, anywhere on or near the Earth, from a global and homogeneous reference, regardless of atmospheric conditions, based on a satellite-receiver system (Monico, 2008, Silva and Segantini, 2015). Georeferencing allows spatial localization of features on the Earth's surface, using a reference system. From topographic and geodesic measurements, it is possible to link the object to be modeled with a reference system.
The aim of this work, considering the scientific contribution, is to propose a new methodology to test the positional accuracy of three-dimensional products obtained by near-range photogrammetry. This paper deals with the use of topographic and geodetic techniques for the georeferencing of three-dimensional models produced by close-range digital photogrammetry, of the architectural structure in homage to the hero of the Pernambucan Revolt, João Fernandes Vieira, located at the Recife Campus of the Federal University of Pernambuco (UFPE). For the later purpose, the theoretical foundations of the issues addressed in this academic article are presented first. This is followed by an analysis of the methodology employed (including the techniques and programmes used), and the results obtained, as well as relevant discussions and conclusions.
Photogrammetry and Terrestrial Photogrammetry
Photogrammetry is a remote measurement technique that allows the three-dimensional reconstruction of objects from photographs. This reconstruction is obtained through the internal and external orientation (both absolute and relative) of the model (Riviero et al., 2013).
To use any methodology based on photogrammetry, it is necessary to define the following: image acquisition, interior orientation (camera calibration) and exterior orientation (special resection and intersection) (Martín et al., 2013).
The interior orientation is obtained through the referencing of the image, concerning the photographic camera, from the reconstruction of the perspective of the package at the moment of image capture, which means the reconstruction of the interior camera-image system. The pictures are freely arranged in space, isolated from each other, and saved as simple digital files, without metric relations, which means using only the system of coordinates expressed in pixels, characteristic of digital images (Coelho & Brito, 2007).
The mathematical modelling of the camera calibration describes the relationship between the coordinates of three-dimensional points and their projections onto the image plane, in other words, the optical geometry of imaging. The parameters of the internal orientation are defined by the camera calibration, with the main elements being the position of the main point, the focal distance, the lens distortions (tangential and radial), and the dimensions of the sensor (Martín et al., 2013).
The external orientation consists of obtaining the position and altitude of the camera at the time each photographic image is collected, relative to the spatial-object reference point. An image is properly externally oriented when six external orientation parameters have been defined: camera rotation angles or altitude of the camera (^, œ and k) and the coordinates of the perspective centre in the object space (Coelho and Brito, 2007).
These very concepts are also addressed in detail by Kraus (1993), Mikail et al. (2001), Kasser and Egels (2002), Ahmed et al. (2012), Koken et al. (2014), Reinoso-Gordo et al. (2020), among others.
In this article, however, a part of Photogrammetry is used, known as Terrestrial Photogrammetry, also known as Close-Range Photogrammetry, because data acquisition takes place with the sensor located at or near the Earth's surface, usually at a distance of less than 100 metres between camera and object (Jiang et al., 2008). This issue has also been addressed, in recent years, in applications presented in the works of Frastia (2009), Mustaffar et al. (2012), Kwak et al. (2013), Koken et al. (2014), Shortis and Shager (2014), Colorado and Santos (2015), Santosi et al. (2015), Basnet et al. (2016), Cârlan and Dovleac (2017), Fu et al. (2017), Long et al. (2017), Bill et al. (2022), Ferencík et al. (2022), Gnann et al. (2022), Illmann et al. (2022), Lauria et al. (2022), Maric et al. (2022), Murtiyoso et al. (2022), Nategh et al. (2022), Paixão et al. (2022), Petruccioli et al. (2022).
Essential Concepts of Modern Topography
Establishing the coordinates of different points is one of the objectives of Topography. These coordinates can be based either on local references, or on general, regional, or national references. In addition, as reported by Gonçalves et al. (2012), the connection to the network takes place by using cartographic coordinates. This means that, at the place of the operation, there must be one or more points with known coordinates according to the cartographic system to be represented. Thus, coordinate transformations must be considered and also the Local Topographic System, addressed in the recently published Technical Standard NBR 14166 (Brazilian Technical Standards Association [ABNT], 2022).
The local topographic system is a Cartesian system, comprising three axes orthogonal to each other; however, its directions do not always follow conventional guidelines. In the case of Brazil, the system used in municipal studies for registration purposes is known as the Local Topographic System (STL, for its Portuguese acronym), which is defined by the technical standard NBR 14166 (Brazilian Technical Standards Association [ABNT], 2022) as a system of flat and rectangular coordinates (X and Y axes), representing the planimetric location of the points and having the same origin as the STL, which corresponds to a point with known geodesic coordinates (Monico, 2008).
Global Navigation Satellite System - GNSS
This system allows a swift and precise three-dimensional positioning, at any point on the Earth's surface, regardless of atmospheric conditions. Regarding the interest in applications to Topography, in a nutshell, the following points must be considered: there is no need for visibility between stations; the accuracy, hardly affected by atmospheric conditions, is more convenient and also faster than conventional methods; and the fact that the results thus obtained are connected to a globally unified coordinate system (Gonçalves et al., 2012). It is also necessary to consider the evolution of this positioning system and the wide range of different techniques used, an issue which is widely addressed and discussed in many books, articles and research studies, such as those by Leick (1995, 2004), Fraser et al. (2005), Colombo (2008), Monico (2008), Cintra et al. (2011), Leick et al. (2015), Um et al. (2020), Egea-Roca et al. (2022).
Integration between GNSS and Topography
In GNSS studies, there are situations where it is impossible to use a receiver on all the vertices to be studied and surveyed, due to the occurrence of signal obstruction. In these situations, the most feasible solution would be to combine different GNSS positioning techniques with topographic techniques such as polygonization, irradiation and intersection. Thus, the integration of the results obtained, by topographic and GNSS surveys, requires compatibiliza-tion, and it is also necessary to perform a conversion to the same reference point, by the transformation of the coordinates obtained with GNSS that are associated with a geodesic coordinate system for an STL. The operation under the STL is essential, since it is not necessary to proceed to measurement reductions (Monico, 2008). The conversion methodology has been explained in detail in the new Brazilian regulation which is defined by the technical standard NBR 14166 (Brazilian Technical Standards Association [ABNT], 2022).
Methodology
This section describes a general outline where the general methodology presented in Figure 1. can be observed.
Equipment Selection
GNSS Receptor
For the implementation of planimetric geodesic support, dual frequency GNSS receivers of the Topcon HiPer II model were used. This equipment has established accuracies for the relative static lifting mode (±3mm + 1ppm) and (±5mm + 1.4ppm), along the horizontal and vertical components, respectively.
Total Station
The three-dimensional coordinates of the control points were measured with a Topcon total station, model GPT-3200N. The technical specifications of the acquisition equipment include angular accuracy of 5"; reach for distance measurements of 400 metres (without prism) and 3,500 metres (with prism), and distance measurement accuracy between (±3mm + 2ppm) in the measurement without prism and (±2mm-2ppm) in obtaining measurements with prism.
Digital Level
For the implementation of altimetric topographic supports, the measurements were made with vertical readings, using a Leica digital level, model DNA03. This allows distance measurements with the use of Invar devices, from 1.80 to 110.00 meters, with a standard deviation of 0.3 mm for height measurement components.
Digital Camera
A Canon EOS 5D camera with a nominal focal length of 50 mm and a CMOS sensor measuring approximately 24 x 35 mm was used to take the photographs, generating images in the 2,912 x 4,368-pixel format.
Data and Camera Preparation Targets
In the planning phase, the size of the lenses to be attached to the architectural structure was established by measuring the distance between the camera and the object to be photographed. This distance is linked to the height of the object that must fit into the image plane of the camera. The height of the object was established with the aid of a tape measure and a beacon, having obtained a measurement of about 5 meters, and for the distance between the camera and the object, a distance of 9.5 meters was obtained. With these values, and with the camera calibration parameters within the Photomodeler programme environment (Photomodeler, 2013), 161 different targets were generated (Figure 2), distributed over 27 pages. As for the geometry of the inner target radius and the outer target diameter, the values obtained were 7.01 mm and 49.07 mm respectively. The Photomodeler generated targets in different formats, to assist in the automatic target identification phase, which was used as part of the interior orientation.
Camera Calibration
A grid with a distribution of 144 points, of which four were controls, were used for the calibration process. Three images were obtained with the camera positioned according to three rotations (9 = 0°, 9 = -90° e 9 = 90°) around the grid, giving twelve images in total. In the Photomodeler program (Photomodeler, 2013), the grid images were inserted in different positions and processed. In this way, it was possible to obtain data concerning the internal geometry of the calibration of the Canon EOS 5D camera (Table 1).
Photogrammetric collection
The photogrammetric collection was carried out with the aid of a Canon EOS 5D photographic camera, calibrated to improve the accuracy and results of a three-dimensional model. Thus, photographs with the optical axis of the camera placed in a position close to the horizontal were obtained, and then the photographs from around the object were collected, so that some areas with overlapping, for the identification of homologous points were collected. In the photogrammetric study, 4 photographs of the same shot were obtained, thereby producing a total of 64 photographs (Figure 3). This condition allowed to choose the best photograph in terms of lighting, a condition that defined the excess of brightness and reflection of the image, thus producing a better quality in the identification of the targets.
Field data conversion
To establish a link between the three-dimensional coordinates of the targets that are part of the architectural structure and the reference topographic system, networks were devised for the planimetric geodesic support, the altimetric topographic report, and the transformation of the control points of the structure into the local topographic system of the campus of the Federal University of Pernambuco (UFPE).
Planimetric geodetic support
A network composed of four points was established as planimetric geodetic support in SIRGAS 2000, and then converted to topographic coordinates in the local topographic system. These support bases were used in the study of the coordinates of the targets to be surveyed by classical topography. At this stage, the receivers were Two Topcon Hiper II dual frequency GNSS, using the static relative survey technique, with a tracking time of 20 minutes, in two observation sections, giving a total of 40 minutes, with a 5-minute break between observations.
As mentioned in Table 2 below, two stations were used as control points for the planimetric geodesic support network: (a) RECF, which is part of the Brazilian Network of Continuous Monitoring of GNSS Systems, maintained by the Brazilian Institute of Geography and Statistics (IBGE); (b) EPS-5, which is part of the Registration Reference Network of the Campus of the Federal University of Pernambuco (UFPE), in Recife, Brazil.
Table 2 Coordinates of the geodesic stations for planimetric control.

Source: author's elaboration (2020)
For post-processing and any adjustments to the network for planimetric geodesic support for GNSS observables collected in the field, the Topcon Tools programme was used, generating Table 3.
Altimetric topographic support
For the altimetric component of the support geodesic network, an altitude transport operation for the points that were part of this network (Table 4) was performed, with the application of the composite geometric levelling methodology, taking as level of reference the RN 3641B with an orthometric altitude of 8.9217 metres (comparing with tide gauge altimetric data for Imbituba and belonging to the official adjusted altimetric network of the Brazilian Institute for Geography and Statistics - IBGE). For this purpose, levelling and counter- levelling procedures with the use of levelling brackets to control the propagation of errors were used.
Local Topographic System
To facilitate calculations and simplifications in topographic applications, the geodetic coordinates have been transferred to a local topographic plane (PTL, for its Portuguese acronym), thus giving rise to the local topographic coordinate system, considering that the coordinates in the UTM system require the planar distance to be transformed into its equivalent distance along the topographic surface, applying the linear deformation coefficient and also the expansion factor. For this procedure, the GeoBASE software has been used, thus transforming the UTM coordinates of the planimetric support network to the local topographic system linked to the Registration Network of the campus of the Federal University of Pernambuco (UFPE) in the city of Recife, Brazil. Thus, Table 5 was generated, as shown below.
Table 5 Coordinates of the planimetric geodesic support network in the local topographic system.
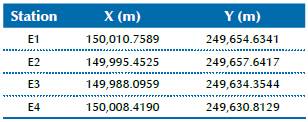
Source: author's elaboration (2020).
For the calculation of the three-dimensional coordinates in the local topographic system of the control points fixed to the architectural structure, the Topcon Link software was used, and the coordinates of the supporting geodetic planimetric network in PTL with the respective orthometric altitudes (Table 6). This means that, by using topography, 75 control points were obtained around the architectural structure, out of the 583 targets attached to the monument.
Georeferencing of 3D models using Photomodeler
For the preparation of georeferencing of 3D models (Figure 4), using the Photomodeler programme (Photomodeler, 2013), it was necessary to establish a definition of absolute orientation. In this process, the actual scale and also the rotation of the axes (X, Y and Z) of the three-dimensional model were established, based on a set of three known coordinates, obtained through topographic and geodetic techniques, and coinciding with points in the three-dimensional model. Subsequently, a georeferenced three-dimensional model was generated, with dimensions associated with the local topographic plane. Points P10, P17 and P20, obtained through topographic and geodetic techniques were used as parameters for the absolute orientation (Table 7).
Results
For the validation of the georeferencing of the architectural structure from the three-dimensional coordinates of the targets (control points), established by topographic and geodetic positioning techniques, a comparative analysis of discrepancies was carried out (Table 7), between the linear measurements obtained by direct measurement, and the linear measurements obtained from the topographic coordinates in PTL (X, Y, h). Thus, the equation of the distance between two points in three-dimensional space [1]) and the discrepancies found between direct linear measurements and those obtained from UTM system coordinates (E, N, Orthometric Altitude) was applied, extracted from coordinated points in a CAD environment with the help of the DIST command (distance between points). This was possible because the work took place in a very limited area, without considering the effects of the Earth's curvature.
Discussion
These results are summarised in Table 8, which presents the comparison between the distances obtained by direct measurement and by topographic coordinates in PTL (X, Y, h). The results show very minor discrepancies, namely: a) the line formed by points 24 and 25 showed a discrepancy of 1.9 mm; b) the line formed by points 25 and 26 showed a discrepancy of 0.6 mm; c) in the case of the alignment between points 27 and 28, there was a discrepancy of 1.2 mm, and d) the line formed by points 28 and 29 showed a discrepancy of 0.9 mm. In the georeferencing of control points using linear measures extracted from the UTM system (E, N, Orthometric altitude), where there was no reduction of measurements, the following discrepancies were obtained: a) 8.6 mm for the alignment of points 24 and 25; b) for the line formed by points 25 and 26, there was a discrepancy of 17.8 mm; c) for the alignment of points 27 and 28, the discrepancy was 9.4 mm; and d) for the alignment between points 28 and 29, the discrepancy found was 10.2 mm. It was also observed that, when PTL coordinates were used, the error was between 0 and 2 mm, while when georeferencing was used, with coordinates in the UTM system, the error was in the range between 0 and 20 mm.
Conclusion
This methodology was based on topographic and geodetic techniques to support positional control in the georeferencing of products prepared by Digital Terrestrial Photogrammetry in the three-dimensional modelling of architectural structures. In addition, this work also addressed georeferencing with the use of UTM and the local topographic system, the analysis of the accuracy of the results, and suggestions to obtain better quality results.
In the process for the georeferencing of architectural shapes, either co-ordinate systems of the Local Topographic Plan or those of UTM may be used, although care must be taken in the case of architectural structures with high shapes, sizes, and volumes. This is because, considering that the architectural structure georeferenced in this work (João Fernandes Vieira: Honour to the hero of the Pernambucan Revolt) is quite small, due to its typology and measurements, it should be noted that the errors obtained in lines formed by coordinate points are between zero and 2 mm for coordinates in PTL and between 0 and 20 mm for coordinates in the UTM system. This shows that obtaining PTL coordinates leads to more accurate and better-quality results. On the other hand, the use of UTM coordinates could worsen the accuracy of the modelling, since the UTM coordinate points that generate the shapes do not undergo any reduction to a flat surface for the measurements thereof.
For georeferencing using the Photomodeler program (Photomodeler, 2013), it is sufficient to insert three points with coordinates linked to the coordinate system of interest. Thus, from a practical point of view, it is not necessary to perform an abundant three-dimensional survey of the control points, which facilitates processing and results in better products for future assignments.
Considering future research studies, a study is suggested to propose an official standard for the definition of classes to carry out Terrestrial Photogrammetric Surveys, considering also applications and even the concept of level of detail (LOD), widely used in 3D SIG modelling (3D Geographic Information System). In addition, another possibility is the application of simulations, considering the admissible errors and sample size, necessary for the approval of a compliant work project or the rejection of a study with this characteristic but which is not compliant (user risk and producer risk). This topic, and a more in-depth study, would be even more timely, also considering the significant increase in the use of drones, which could be employed in terrestrial photogrammetry tasks, but which do not yet show a mathematically proven level of reliability, even though this market has been showing incredible development.
Nex et al. (2022) state that the use of Unmanned Aerial Vehicles (UAVs) has skyrocketed in the last two decades and they have become the most popular instruments for a wide range of applications. The development of best practices for high-quality UAVs depends on interdisciplinary research that promotes integration between different expertise and the combination of hardware and software components on the same platform. Researchers can take oblique/horizontal UAV images from the facade to process images with software (PIX4D, AGISOFT, etc.) dedicated to photogrammetry issues. There are numerous successful examples in the literature. Li and Shan (2022) have proposed the reconstruction of a building model from 3D point clouds. They have extracted graphical primitives of a building from digital surface modelling produced by collecting digital drone scenes and laser profiling. Kush-waha et al. (2019) have promoted point cloud segmentation to obtain trees, building roofs, and building facades. And after all, when they compare the results with the manual points cloud identification of the same, they obtain overall accuracies for roof and building façade segmentation of 90.86 % and 84.83 %, respectively. The results and analysis of these investigations indicate the importance of processing oblique/horizontal digital images, such as a 3D point cloud based on UAV imagery, which is a suitable source for obtaining facade features.


























