Un estudio multinivel del rendimiento escolar en matemáticas para tercer grado de educación básica primaria en América Latina¹

A Multilevel Study of School Performance in Mathematics for Third Grade of Basic Education in Latin America

Um estudo multinível do rendimento escolar em matemáticas para terceiro grau de educação básica primária em América Latina

Juan Carlos Zambrano Jurado²
Docente e investigador de la Universidad del Valle, Cali, Colombia
juan.carlos.zambrano@correounivalle.edu.co

Recibido: 30/06/15
Aprobado: 24/11/15

Resumen

Este estudio realiza, en tres etapas, un análisis multinivel del rendimiento escolar en matemáticas, para identificar los factores familiares y escolares, y las condiciones socioeconómicas de los estudiantes; las prácticas y métodos pedagógicos, y la inversión económica, que inciden en el alcance de los logros educativos en el área de matemáticas. Usa datos de 60.325 estudiantes de tercer grado de educación básica primaria, pertenecientes a 15 países participantes en el Segundo estudio regional comparativo y explicativo (SERCE) 2006 en América Latina. Las variables de mayor impacto en el estudio son: sexo, tipo de escuela, zona, recursos de consulta, repetición de cursos, sentido de pertenencia al centro y PIB invertido en educación. Estas variables son explicadas por las características personales de los estudiantes, y las de la institución y el país al que pertenecen.

Palabras clave: calidad de la educación; entorno familiar; efecto escuela; efecto país; análisis multinivel.

Clasificación JEL: C51, I20, I21, I23.

Abstract

This study carried out -in three stages- a multilevel analysis of school performance in mathematics, to identify family and school factors, and socioeconomic conditions of students; practices and teaching methods, and economic investment, affecting the scope of educational achievements in the area of mathematics. Uses data from 60,325 students in third grade basic education, from 15 countries participating in the Second Regional Comparative and Explanatory Study (Segundo Estudio Regional Comparativo y Explicativo -SERCE) 2006 in Latin America. The variables with the greatest impact in the study are: sex, type of school, area, reference resources, repetition od courses, sense of belonging to the center and GDP invested in education. These variables are explained by the personal characteristics of the students and of the institution and the country they belong to.

Keywords: quality of education; family environment; school effects; country effects; multilevel analysis.

Resumo

Este estudo realiza uma análise multinível em três etapas, do rendimento escolar em matemáticas para identificar os fatores familiares e escolares, as condições socioeconómicas dos estudantes, as práticas e métodos pedagógicos, e o investimento económico que incidem no alcance dos desempenhos educativos na área de matemáticas. Utilizam-se dados de 60.325 estudantes terceiro grau de educação básica primaria, de 15 países participantes no Segundo Estudo Regional Comparativo y Explicativo (SERCE), 2006 para América Latina. As variáveis de maior impacto no estudo são: sexo, tipo de escola, setor, recursos de consulta, repetição de disciplinas, sentido de pertencimento ao centro e PIB investido em educação. Ditas variáveis são explicadas pelas características pessoais dos estudantes, da instituição e do país respectivo.

Palavras-chave: qualidade da educação; entorno familiar, efeito escola, efeito país, análise multinível.

Introducción

En la actualidad, la importancia de la calidad en la educación básica es uno de los derroteros internacionales de mayor relevancia para el desarrollo de la educación y una de las áreas de mayor trabajo durante los últimos quince años. La educación de calidad debe ser un derecho para todos los individuos de una sociedad y debe ser tomada como un modelo de desarrollo a implementar por todas las regiones. Los sistemas educativos tienen como obligación mejorar los procesos en los cuales los estudiantes pueden conseguir otros logros educativos (Unesco 1990). Se considera como un paso importante en el mejoramiento de los resultados educativos el entendimiento de variables relacionadas con el éxito académico.

Organizaciones internacionales como la Organización para la Cooperación y el Desarrollo Económico (OCDE), la Asociación Internacional para la Evaluación de Logros Educativos, la Unesco y la Unicef han patrocinando una serie de exámenes internacionales y de aprendizaje a gran escala para establecer medidas de entendimiento sobre la calidad de la educación (Rodríguez, Simpson y Heyman 2004), con el objetivo de comparar entre los países participantes los logros de los estudiantes en términos de normas reconocidas internacionalmente. De esta forma, la calidad de la educación se puede expresar de diversas maneras y puede estar asociada a un conjunto amplio de factores relacionados con el alumno, la escuela, y las políticas económicas y educativas en los diferentes países.

La mayoría de los países de América Latina han logrado ampliar su cobertura en educación primaria y han desarrollado sistemas nacionales de evaluación de la calidad, pero aún no se realizan pruebas periódicas que permitan comparar los resultados internacionales. La prueba TIMSS realizada en 1994-1995 es la primera experiencia comparable en la cual se incluyó a Colombia como único país latinoamericano. Esta prueba estuvo orientada a evaluar los niveles de desempeño en matemáticas y ciencias en distintos grados. Posteriormente, se aplicó en 1998-1999 y en 2003; de acuerdo con los resultados de estas pruebas, los países latinoamericanos (Colombia y Chile) registran desempeños sustancialmente por debajo del promedio internacional y se ubican entre los últimos lugares, reflejando las disparidades existentes entre los mundos desarrollado y en desarrollo. Para el caso particular de los países de América Latina, el "Laboratorio Latinoamericano de Evaluación de la Calidad de la Educación" (LLECE), constituido en 1994 y coordinado por la oficina regional de la Unesco, adelantó en 1997 el Primer Estudio Internacional Comparativo en las áreas de Lenguaje y Matemáticas (PERCE), para niños en tercero y cuarto grados de educación primaria, y en el 2006 el Segundo Estudio Regional Comparativo y Explicativo (SERCE) para niños en tercero y sexto grados de educación básica (Iregui, Melo y Ramos 2006).

En esta línea, se plantea como hipótesis que existen diferencias significativas en la calidad de la educación básica en América Latina en cuanto a estudiantes, escuelas y países medidas a través de los resultados obtenidos en las pruebas SERCE 2006. Así, el objetivo de esta investigación es identificar mediante el uso de algunos ejercicios econométricos con estructuras multinivel, el impacto de algunas variables del entorno del alumno, del ambiente escolar y del país, que permitan explicar las diferencias observadas en el alcance de logros en matemáticas. De esta forma, la investigación que se presenta tiene como aporte estimar el efecto escuela y el efecto país en Latinoamérica relacionados con el logro escolar de sus estudiantes y analizar la relación existente entre el logro, el nivel socio-económico de las familias de dichos estudiantes y el clima escolar aproximados con variables de su entorno. Con ello se quiere mostrar evidencias sobre dichos resultados que se estimen con el fin de determinar cuál de estos efectos influye más en el alcance de logros y discutir algunos aspectos sobre política educativa en la escuela básica primaria.

En este documento se revisan ciertos estudios relevantes sobre calidad de la educación, se plantea la metodología y la definición formal del modelo multinivel de tres etapas. Para finalizar, se realiza el proceso de modelización y análisis de resultados apoyado en las estructuras multinivel, que permitirá comparar la influencia de las principales variables que intervienen en el rendimiento académico de los estudiantes y, posiblemente derivar algunas sugerencias que permitan identificar aspectos a mejorar del sistema educativo, en el área específica de Matemáticas.

1. Antecedentes

El trabajo considerado como pionero en el área de investigación en educación es el de Coleman (1966), el cual analiza los efectos sobre el nivel del logro educativo por parte de los antecedentes familiares, educación de los padres, gobernanza escolar, comportamiento y diferencias en la calidad escolar. Por su parte Bowles y Levin (1968) contradicen las conclusiones del Informe Coleman demostrando que las técnicas de "incorporación progresiva de variables" habían sido aplicadas sin advertir la existencia de una alta correlación entre las variables representativas del hogar y de la escuela que invalidaba los resultados obtenidos.

Lee y Barro (2001) usan TIMSS para un número amplio de países para demostrar que las características familiares, las tasas de repetición, las tasas de deserción y los recursos escolares tienen un efecto significativo sobre el desempeño de los estudiantes. Sugieren que más recursos escolares y especialmente el tamaño de clases más pequeñas pueden mejorar los resultados educativos.

Entre los trabajos que se ocupan de los recursos, el rendimiento y la responsabilidad escolar se encuentra el estudio de Hanushek (2004a), en el cual se sugiere que la relación entre los recursos de la escuela y el rendimiento escolar dependen de las interacciones entre los recursos, la calidad de los profesores y otros insumos. Hanushek (2004b) analiza la vinculación de los incentivos o las consecuencias disciplinarias al desempeño escolar y encuentra que los sistemas de responsabilización aumentan los niveles del logro de los estudiantes. Hanushek y Luque (2003) usan las pruebas TIMSS 1995 en 40 países para mostrar que los niños de las familias con mayores recursos educativos en el hogar presentan mayor rendimiento, además encuentran limitación en la fuerza de los recursos del sistema para obtener un mejor desempeño de los estudiantes.

En Estados Unidos, los trabajos de Greenberg (2004) y Bedard y Dhuey (2006) determinan que existen fuertes conexiones entre el logro académico, la participación paterna y el comportamiento de los estudiantes según la edad; el comportamiento de los estudiantes está directamente relacionado con el mayor desempeño en matemáticas. Además, estos autores establecen que las diferencias iniciales de madurez/edad tienen efectos positivos en el desempeño de los estudiantes.

El análisis del entorno escolar, la autonomía escolar, la influencia de los profesores sobre los métodos didácticos y del estudiante en el alcance de logros es un punto fuerte en el estudio de Woessmann (2003), quien utiliza los resultados de las pruebas TIMSS para 39 países estableciendo que las diferencias entre las escuelas explican las diferencias internacionales del rendimiento de los estudiantes en las pruebas de logro cognoscitivo. Hanushek y Woessmann (2007) establecen que las características comunes de los profesores no están estrechamente relacionadas con el desempeño de los estudiantes, excepto el nivel de educación del docente. La asignación de recursos, la reducción del tamaño de las clases, los sueldos de los profesores, el gasto en las escuelas, entre otros, tienen un pequeño impacto en el desempeño de los estudiantes.

En América Latina y el Caribe se destacan numerosos estudios sobre eficacia escolar y se enfocan principalmente sobre los factores asociados al rendimiento escolar. Dentro de este marco de referencia están los estudios de Delprato (1999), Cervini (2004), Cueto y Secada (2004), Carvallo (2005), Concha (2006), Fuentes et al. (2006), Mizala, Romaguera y Reinaga (2006), Murillo (2006), Vegas y Petrow (2007), Murillo y Roman (2011), Piñeros y Rodríguez (1999), Gaviria y Barrientos (2001) y Barrera y Gaviria (2003). Algunos de los resultados más importantes son:

En primer lugar el trabajo de Delprato (1999) con datos de las pruebas de rendimiento realizadas por el Sistema Nacional de Evaluación de la Calidad (SINEC) de la educación en Argentina identifica mediante una estructura jerárquica de dos y tres niveles los determinantes del rendimiento educativo en básica primaria para los años 1993 y 1997; variables como el nivel socioeconómico promedio de la escuela, variables de estrato y recursos de capital, el PIB de las jurisdicciones poseen un impacto positivo con el rendimiento del estudiante en las distintas jurisdicciones.

Cervini (2004) usa los datos de las evaluaciones nacionales de Argentina para las pruebas estandarizadas en matemáticas y lenguaje. Destaca que la distribución del rendimiento está afectado por la desigualdad socioeconómica institucional del sistema educativo, donde el capital cultural, familiar y contextual es el factor más importante; destaca el efecto de la "composición" (orden social, académico, de género) y del "ethos" estudiantil (promedio de valores del conocimiento en matemáticas y autoconceptos de los alumnos).

Concha (2006) describe los factores asociados (de directores, docentes, padres y supervisores) que conducen a que los alumnos pertenecientes a escuelas de alta vulnerabilidad socioeconómica alcancen mejores niveles de aprendizaje que los esperados en Chile. Usa las pruebas del Sistema Nacional de Medición de la Calidad de la Educación (SIMCE) en 1992 y 1994 en los cuatro años básicos y destaca que la organización de la gestión pedagógica y administrativa está muy asociadas a los altos niveles de logros alcanzados.

Vegas y Petrow (2007) hacen un análisis para América Latina y el Caribe, centrado en tres partes; el papel del aprendizaje estudiantil en la educación, factores y políticas que afectan el aprendizaje estudiantil y el aseguramiento de la calidad en la educación; destacan la dependencia de las interacciones entre los factores de estudiantes y las escuelas, los factores institucionales y la política educativa, así como el contexto económico, político y social sobre el logro de los estudiantes.

Murillo y Roman (2011) desarrollan un estudio multinivel para analizar el aporte de los efectos escolares al rendimiento de los estudiantes en América Latina y se compara con el efecto del nivel cultural y socioeconómico de las familias. Usan los datos del SERCE con modelos multinivel de tres niveles. Entre sus resultados encuentran que el efecto escolar neto para el conjunto de América Latina se encuentra entre 17,6% y 22,3%, con grandes diferencias entre países; y que el efecto del nivel cultural y socio-económico ese encuentra entre 10,8% y 14,0%. Con ello se deduce la capacidad de la escuela para compensar las diferencias de origen.

Otro estudio de importancia es el de Unesco (2008) que en su primer reporte de los resultados del SERCE 2006 presenta el resumen del proceso, aplicación, resultados y hallazgos en matemática, lectura y ciencias de los estudiantes que cursaban tercero y sexto grados de educación primaria entre 2005-2006. En este estudio se encuentra que el clima escolar, la infraestructura y servicios, así como la disponibilidad de libros en la biblioteca se relacionan consistente y positivamente con el logro en casi todas las áreas y grados evaluados. El clima escolar es la variable que más contribuye a la explicación del logro de los estudiantes. Con respecto a las variables del aula, solamente los años de experiencia del docente tienen una relación positiva y consistente con el desempeño. El nivel socioeconómico y cultural promedio de la escuela, el género, el hablar una lengua indígena, el trabajo infantil, los años de escolarización previa y el nivel socioeconómico y cultural del estudiante se relacionan consistentemente con el logro. Sin embargo, el factor que más influye en el desempeño es el nivel socioeconómico y cultural promedio de las escuelas. Por otro lado, las variables del estudiante explican solamente una pequeña porción de la variación en el aprendizaje.

En Colombia, Piñeros y Rodríguez (1999), usando una muestra de los exámenes de Estado de 1997, destacan aspectos como el impacto positivo que presentan el nivel socioeconómico y el nivel sociocultural en lenguaje y menos para matemáticas y ciencias. Observaron que la calidad de la escuela tiene mayor impacto sobre el desempeño en matemáticas y ciencias, y que permanecer en la misma escuela durante toda la secundaria tiene una repercusión positiva sobre el desempeño de los estudiantes. Las escuelas explican 15,18% de la varianza entre estudiantes en escuelas privadas y 12,16% en escuelas públicas. Los autores destacan la relación entre el nivel socioeconómico y el desempeño académico en las escuelas privadas.

Las relaciones de factores como la educación de los padres, la calidad de los establecimientos y el tipo de escuela son analizadas en los trabajos de Gaviria y Barrientos (2001) y Barrera y Gaviria (2003), quienes toman como fuente principal el examen de Estado y los resultados del DANE de 1999 en Bogotá y el resto del país, y destacan los siguientes aspectos: la educación de los padres afecta significativamente el logro, este disminuye sustancialmente cuando se controla el efecto de la escuela a la que asiste, las familias de bajos recursos tienen restricción de acceso a escuelas de alta calidad. Las diferencias en el logro individual se explican por las diferencias entre las escuelas. Tanto las escuelas privadas como la educación promedio de los profesores y el número de profesores por estudiante están asociados positivamente con el logro de los estudiantes, pero para las escuelas públicas no hay ninguna asociación entre estas características y el logro.

Zambrano (2013) realiza un análisis multinivel para estudiantes de cuarto grado de educación básica, usando las pruebas TIMSS 2007 para Colombia. Como resultado se identificó mayor rendimiento de los niños en comparación con el logrado por las niñas. De las variables incluidas en el estudio, las de mayor impacto son: el tipo de escuela, gusto por las matemáticas, zona de la escuela y gusto por la escuela, explicadas por características personales y de la institución a la que pertenecen los estudiantes.

2. Metodología

El punto de partida para estudiar la relación de efectividad existente entre el resultado del aprendizaje en las escuelas y el conjunto de recursos disponibles con que estas cuentan para resolver el proceso de enseñanza y aprendizaje es la noción de función de producción educativa (Levin 1983; Coombs y Hallak 1987). Según Hanushek (1970), los factores actúan de manera conjunta, se agrupan según su naturaleza y se pueden incorporar a una función de producción educativa que expresa de la siguiente forma:

Y_it = F(B^(t)_i + P^(t)_i + I_i + S^(t)_i) (1)

Donde:

Y_it hace referencia al resultado educativo del estudiante i-esimo en el período t.

B^(t)_i es un vector que corresponde a los factores relacionados con la familia del estudiante i-esimo acumulados hasta el período t.

P^(t)_i es un vector que corresponde a los factores asociados a los pares (compañeros) del estudiante i-esimo acumulados hasta el período t.

I_i corresponde a las habilidades innatas de cada estudiante.

S^(t)_i es un vector que corresponde a los factores de la escuela del estudiante i-esimo acumulados hasta el período t.

Sin embargo, la investigación sobre eficacia escolar está dirigida al análisis de los factores que hacen que los alumnos de una escuela tengan mejores resultados educativos en comparación con los de otras. Todo este proceso desencadenó así una evolución en los modelos y las técnicas de análisis utilizadas, las variables y los factores estudiados, los instrumentos de recogida de datos, etc., encontrando siempre como principal dificultad metodológica la imposibilidad de utilizar metodologías de carácter experimental con manipulación del tratamiento (Goldstein 1997), en este caso la asistencia a un centro u otro, para comprobar los efectos de un centro y sus variables.

Aitkin y Longford (1986) demostraron que los modelos de regresión lineal —técnica usualmente utilizada para estudiar cómo un conjunto de variables explicaban una variable producto— solo podían ser empleados en un caso muy especial: cuando las observaciones eran independientes (Gelman y Hill 2006; Goldstein 2003; Heck y Thomas 2000; Hox y De Leeuw 1998). Sin embargo, la realidad de nuestros sistemas educativos —donde los estudiantes están agrupados en aulas o cursos, distintas aulas están agrupadas en escuelas y las escuelas en distritos o provincias o regiones o países— afecta el supuesto de independencia de las observaciones, independencia entre las variables y el error de estimación del modelo. Compartir el mismo contexto causa su dependencia, los errores estándar estimados de las pruebas estadísticas tradicionales aparecerán claramente subestimados y ello conducirá irremediablemente a que la mayoría de los resultados no sean significativos (Hox 1995). Por otro lado, las funciones de producción educativa uniecuacionales no toman en cuenta el carácter esencialmente jerárquico de las relaciones que se pretenden estudiar, y por esto han recibido fuertes críticas en los últimos años (Rowe, Hill y Holmes-Smith 1995; Wenglinsky 1998; Bryk y Raudenbush 1992; Monette, Shao y Kwan 2001).

Los llamados modelos multinivel aparecen como una alternativa para solucionar dichas dependencias. Efectivamente, proponen una estructura jerárquica de análisis dentro de la cual se pueden reconocer los distintos niveles en que se articulan los datos. En el caso de los datos educativos, los alumnos están agrupados en aulas, las aulas en centros docentes y los centros en contextos (distritos escolares, comunidades autónomas, países, etc.), elaborando así un submodelo diferente para cada nivel.

En este trabajo se pretende desarrollar un modelo específico que identifica tres niveles de análisis: el primer nivel en el cual se considera el conjunto de variables personales y del hogar de pertenencia que afectan el rendimiento de cada alumno; el segundo nivel contempla las variables referentes a las características escolares y del profesor; y el tercero identifica el efecto asociado con las variables del país.

3. Fundamentos del modelo multinivel

La modelación teórica de este proyecto está fundamentada en la metodología de los modelos multinivel y en el problema de investigación en educación, que permiten trabajar unidades de análisis de forma simultánea. Efectivamente, proponen una estructura de análisis dentro de la cual se pueden reconocer los distintos niveles en que se articulan los datos.

Los modelos multinivel son ampliaciones de los modelos de regresión lineal clásicos, de tal forma que en realidad son varios modelos lineales para cada nivel. Así, los modelos del primer nivel están relacionados con uno de segundo nivel en el que los coeficientes de regresión del nivel uno se regresan en un segundo nivel de variables explicativas y así sucesivamente para los diferentes niveles.

Para el estudio de los modelos multinivel se tomó como referencia principal el libro Modelos jerárquicos lineales de Gaviria y Castro (2005) y el trabajo de Delprato (1999). Por este motivo, la presentación siguiente, en gran medida, sigue su notación y línea argumental.

3.1. Modelo general de tres niveles

Como su nombre lo indica el modelo está compuesto por tres submodelos. Por ejemplo, en nuestro caso el problema de investigación es sobre datos de estudiantes anidados dentro escuelas y las escuelas dentro de países; el modelo del nivel 1 representaría las relaciones de las variables del estudiante, el modelo del nivel 2 capturaría la influencia de los factores escolares y el modelo del nivel 3 captura la influencia de los factores relacionados con el país. Formalmente, en esta estructura jerárquica hay i = 1,..., n_jk unidades del nivel 1 (estudiantes), los que se encuentran dentro de j = 1,..., J_k unidades del nivel 2 (escuelas), las que a su vez se encuentran en k =1,..., K unidades del nivel 3 (países).

En el modelo del nivel 1 se representa la variable dependiente para el caso (alumno) i dentro de la unidad j del nivel 2 y la unidad k del nivel 3 como:

Donde:

β_qjk (q=0,1,...,Q) son los coeficientes del nivel 1;

X_qijk es el predictor q del nivel 1 para el caso i en la unidad j del nivel 2 y en la unidad k del nivel 3;

e_ijk es el efecto aleatorio del nivel 1; y

σ² es la varianza de e_ijk, la varianza del nivel 1.

Se supone que el término aleatorio se distribuye normal, esto es, e_ijk ~ N(0,σ²)

En Modelo del nivel 2, cada uno de los coeficientes β^qjk (q=0,1,...,Q) definidos en el modelo del nivel 1 se convierten en variables dependientes del modelo del nivel 2:

Donde:

γ_qsk (q=0,1,...,s_q) son los coeficientes del nivel 2;

W_Sjk es el predictor del nivel 2; y

µ_qjk es el efecto aleatorio del nivel 2.

Se supone que para cada unidad j del nivel 2, el vector (µ_0jk,µ_1jk,...,µ_Qjk) se distribuye normal multivariante, y cada elemento µ_qjk tiene media cero y varianza expresada de la siguiente manera: Var( µ_qjk) = τ_βqq

Para cada par de efectos aleatorios q y q' se tiene: Cov( µ_qjk ,µ_q'jk ) = τ_βqq'

En el modelo del nivel 3, los coeficientes γ_qsk definidos en el modelo del nivel 2 se presentan como variables dependientes en el modelo del nivel 3:

Donde:

α_qsp (p = 1,2,..., Pqs) son los coeficientes del nivel 3;

Z_sk es el predictor del nivel 3; y

v_qsk es el efecto aleatorio del nivel 3.

Para cada unidad k del nivel 3, el vector de efectos aleatorios (α_qsp) se distribuye normal multivariante.

3.2. El modelo nulo

Es un caso particular del modelo anterior. Aquí no existe ninguna variable explicativa, por lo que constituye una herramienta metodológica. Si la varianza de este modelo no es estadísticamente distinta de cero, no tendría sentido incluir variables explicativas en el modelo jerárquico en ninguno de sus tres niveles.

El modelo completo sería:

Donde:

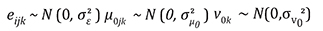
σ²_e es la varianza entre estudiantes,

σ²_µ0es la varianza entre las escuelas y

σ²_v0 es la varianza entre países.

Por lo tanto, si estas tres varianzas no fuesen estadísticamente significativas no tendría sentido introducir variables explicativas debido a que este hecho significaría que no habría nada que explicar (Gaviria y Castro 2005). No obstante, la varianza de cada nivel generalmente es significativa, por lo que el paso a seguir sería introducir variables independientes en cada uno de los niveles que disminuyan la varianza no explicada.

Los estimadores más utilizados en el análisis de regresión multinivel son los estimadores de máxima verosimilitud (maximum likelihood estimators, MLE); la significancia de un predictor viene dada por la ratio entre el estimador del parámetro y su error típico. Este test es conocido como el test de Wald. Se verifica que:

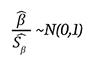o lo que es equivalente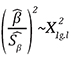

En la práctica, la regla general para determinar la significancia del predictor es

En un modelo multinivel hay dos tipos de parámetros: fijos y aleatorios. Los fijos corresponden a los efectos medios en la población, y son las pendientes y el intercepto. Los aleatorios corresponden a las varianzas y covarianzas de todos los niveles.

Los procedimientos de máxima verosimilitud también producen un estadístico llamado deviance. Este estadístico indica qué tan bien se ajusta el modelo a los datos. Si llamamos L1 al valor máximo de la función de verosimilitud (likelihood) en la estimación de los parámetros del modelo 1, entonces se define la deviance:

Si en el modelo nulo no hay varianza estadísticamente distinta de cero en los niveles contemplados, ningún modelo que se derive de este añadiendo variables explicativas mejorará el ajuste, ya que la varianza del intercepto no es significativamente distinta de 0. Si dos modelos están anidados, es decir, un modelo se obtiene a partir de otro más general eliminando parámetros de este último, entonces podemos compararlos. Para dicha comparación se usa la deviance de cada modelo, ya que la diferencia de las deviances se distribuye como un chi-cuadrado con los grados de libertad iguales a la diferencia del número de parámetros estimados en los modelos que estamos comparando, bajo la hipótesis nula de que ambos modelos son iguales.

La correlación intraclase o auto¬correlación expresa el grado de homogeneidad de los elementos dentro de cada nivel.

4. Población estudiada y descripción de las variables

El Laboratorio Latinoamericano de Evaluación de la Calidad de la Educación (LLECE) es la red de sistemas de evaluación de la calidad de la educación de América Latina, coordinado por la Oficina Regional de Educación de la Unesco para América Latina y el Caribe, con sede en Santiago de Chile.

Conforme a sus objetivos, el laboratorio desarrolló en 2006 el Segundo Estudio Regional Comparativo y Explicativo (SERCE), que evalúa y compara el desempeño alcanzado por los estudiantes latinoamericanos de tercero y sexto grados de educación primaria en las áreas de lenguaje, matemática y ciencias naturales.

El estudio SERCE, que involucró a estudiantes de enseñanza primaria de 16 países , busca explicar sus resultados a partir de distintos factores escolares, de contexto y así generar conocimiento relevante para la toma de decisiones de política educativa para mejorar las prácticas docentes, escolares y con esto, promover una mayor equidad en los aprendizajes.

Su amplia cobertura recoge información sobre los estudiantes y sus familias, los docentes, los directores y las escuelas; permite identificar cuáles son los factores que tienen mayor incidencia en los desempeños de los estudiantes, así como el cumplimiento de altas exigencias teóricas y de método, y la capacidad de generalización: lo que el estudio informa sobre los estudiantes evaluados puede extenderse al resto de los estudiantes de la región y del país. El estudio comenzó en 2002, recogió la información en 2006 y publicó el primer reporte de resultados en Unesco (2008), que son tomados como base para desarrollar la estrategia metodológica en esta investigación.

El SERCE 2006 evaluó una muestra conformada por 96.663 estudiantes de matemáticas de tercer grado de 16 países y el estado de Nuevo León en México con un total de 2.843 establecimientos educativos. La muestra fue diseñada por el SERCE de tal manera que permite comparar información por sector (oficial — privado) y zona (urbana — rural), mas no por departamentos, municipios o regiones; adicionalmente, los cuestionarios de los estudiantes recogieron la información sobre género, lo que también hace posible la realización de análisis basados en esa variable. En este estudio se incluye a 15 países, excluyendo de la muestra a Cuba y al estado de Nuevo León en México. Cuba presenta un sistema educativo que tiene unas características diferentes al resto de países latinoamericanos: por ejemplo, no existen escuelas privadas, el total de la educación es de carácter público, además todo el sistema educativo depende exclusivamente del financiamiento del gobierno, esto no permite establecer un punto de comparación con el resto de los países.

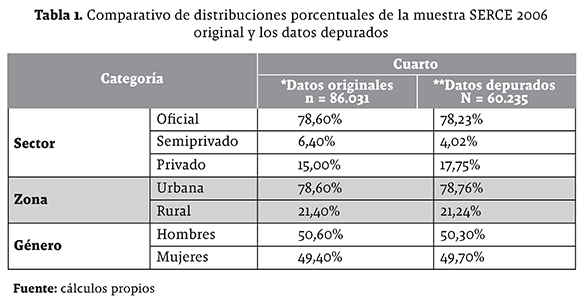
La muestra original sin los datos de Cuba y el estado de Nuevo León es de 86.031 estudiantes correspondientes a 2.500 escuelas en los 15 países. Es de anotar que debido a la existencia de valores omitidos en variables relevantes para el estudio fue necesario un proceso de depuración de los datos que finalmente arrojó una base de datos de 60.235 estudiantes correspondientes a 2.162 escuelas con los cuales se inició el procesamiento de información. En la tabla 1 se muestra que la distribución de las variables sector, zona y sexo de los estudiantes conservan una distribución similar a la de los datos originales.

El promedio general del puntaje en matemáticas en el total de países participantes en el SERCE 2006 es de 505,11 puntos; se destaca el resultado de Cuba, Uruguay y Costa Rica como los países con mayor puntuación; Brasil apenas logra establecerse en la media, al igual que Chile y Colombia; resaltan los bajos resultados de Guatemala y República Dominicana.

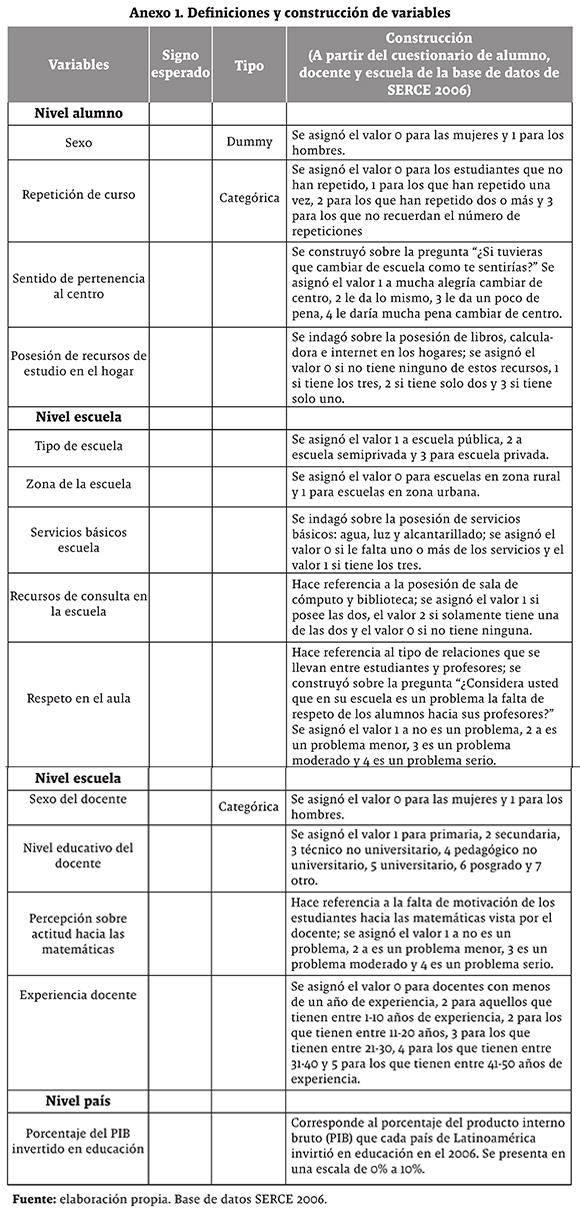
Aunque las pruebas SERCE 2006 cuentan con una gran batería de preguntas sobre los centros educativos, profesores y estudiantes, en este estudio solo se incluyen variables asociadas a tercer grado de educación básica primaria que aparecen como relevantes en la mayoría de artículos sobre calidad de educación y que enfrentan variables de los tres niveles. Es de resaltar que la base de datos para este grado no presenta una variable específica que muestre el índice socioeconómico del estudiante, por tal razón se pretende usar como una proxy del nivel socioeconómico del estudiante la variable de recursos de estudio en el hogar, sin descartar la existencia de algún tipo de sesgo. Siguiendo la línea de Unesco (2008), para evaluar el clima escolar se usan los efectos de las variables sentido de pertenencia al centro de estudios y respeto en el aula; otras variables a considerar son: sexo del estudiante, repetición de cursos, sexo del profesor, nivel máximo de educación alcanzado por el profesor, percepción sobre actitud hacia las matemáticas, experiencia docente, tipo de escuela, zona de la escuela, servicios básicos de la escuela, recursos de consulta en la escuela y el porcentaje del PIB invertido en educación como variables independientes. La variable educación de padres no es considerada para el grado tercero en el estudio SERCE 2006, razón por la cual no se incluye en este estudio. Como variable dependiente se trabajó el puntaje estándar final del estudiante en la prueba SERCE 2006. La descripción detallada de las variables a utilizar en el modelo se presenta en el anexo 1.

5. Modelización y resultados

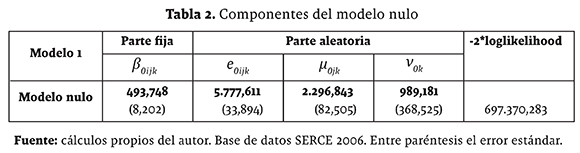
La aplicación práctica y la interpretación de los distintos modelos multinivel se realizan con el software MLWin, editado por el Centro de Modelamiento Multinivel del Instituto de Educación de Londres (Goldstein et al. 2004) y actualmente una de las herramientas más importantes para trabajar modelos con estructura jerárquica. En primer lugar, la representación del modelo nulo realizado muestra que el modelo asume una variable respuesta con distribución normal. El coeficiente beta se encuentra multiplicado por un vector constante que se introduce con la intención de dar el mismo tratamiento al punto de corte que a las pendientes del modelo. El software MLWin muestra también cómo la variación se encuentra estructurada en tres niveles, donde una parte le corresponde al nivel alumnos e_0ijk, otra al nivel escuela µ_ojk y la otra al nivel país υ_ok. En el modelo nulo se observa la existencia de varianza en cada nivel que indica que los sujetos se diferencian entre ellos dentro de los países y dentro de las escuelas.

En la tabla 2, el valor β0_ijk=493,748 es el punto de corte del modelo nulo, es decir, la calificación promedio en matemáticas obtenida por los estudiantes en las pruebas SERCE 2006, con un error típico de 8,202.

Los estudiantes difieren entre ellos en rendimiento: la estimación de la varianza para el nivel estudiante es de 5.777,611 y su error típico 33,894. De igual manera, existen diferencias en los rendimientos de las escuelas (varianza = 2.296,843, error típico = 82,505) y entre los países (varianza = 989,181, error típico = 368,525). Como sucede en los modelos tradicionales, la significancia de un predictor está dada por la razón entre su estimador y su error típico. Si el valor de dicho cociente es mayor a 2 (p < 0,05) el parámetro será significativo. La significación de estos parámetros indica una variación sin explicar entre los rendimientos de los alumnos, los rendimientos de las escuelas y los rendimientos de los países.

Se calcularon las correlaciones intraclase de cada uno de los niveles; esta correlación expresa el grado de homogeneidad de los elementos dentro de cada nivel.

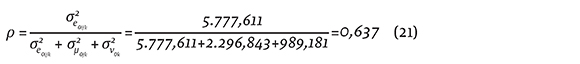
Esto indica que del total de la varianza del rendimiento, 63,7% corresponde a la varianza entre alumnos, 25,3% a la varianza entre las escuelas y 10,9% a la varianza entre países (anexo 2).

Así, la diferenciación del rendimiento de los estudiantes en la prueba SERCE es explicada en 25,3% por el efecto escuela, y en 10,9% por el efecto país. Por lo tanto, todos los esfuerzos se orientan en empezar a introducir variables en el modelo que disminuyan la varianza no explicada.

5.1. Modelo con variables de nivel alumno

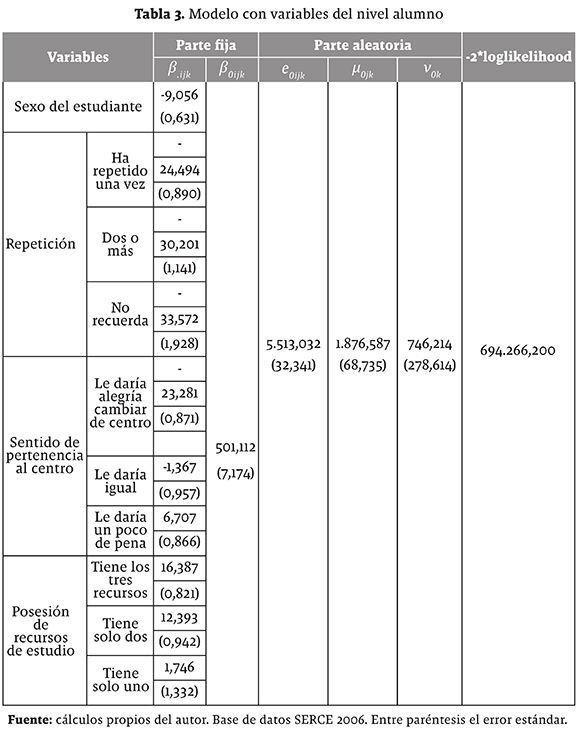
La expansión del modelo se realiza incluyendo variables al modelo inicial (modelo nulo) y verificando la significancia de cada nueva variable, al comparar los valores del estadístico -2*loglikelihood del modelo nulo y los modelos siguientes, lo que permite evaluar el aporte de cada variable; de igual manera la varianza de cada nivel permite analizar cómo la inclusión de cada variable afecta la variabilidad debida a los países, las escuelas y los estudiantes. Es de aclarar que en la estimación de variables categóricas, la omitida es la categoría de referencia sobre la cual se interpretan los resultados. Se inicia incorporando predictores del nivel alumno a la parte fija y aleatoria del modelo, posteriormente las variables de nivel escuela y finalmente las variables del nivel país. En el anexo 2 se puede observar el aporte y la significancia de cada variable al ser incluida una a una en el modelo. En la tabla 3 se puede apreciar un aporte significativo de la variable sexo con un parámetro asociado negativo y significativo (-9,056). Estos 9,056 puntos representan la diferencia en el rendimiento medio en matemáticas entre niños y niñas. En este caso, las niñas obtienen en promedio 9,056 puntos menos que los niños.

Al agregar la variable repetición, se observa un aumento en el punto de corte, ya que ahora se refiere al rendimiento medio de los niños que no han repetido curso. El coeficiente obtenido para esta variable indica que en comparación con los que no han repetido curso (categoría de referencia), aquellos estudiantes que han repetido una vez tienen en promedio 24,494 puntos menos; los estudiantes que han repetido curso dos o más veces tienen en promedio 30,201 puntos menos en las pruebas; y aquellos estudiantes que dicen no recordar el número de repeticiones presentan 33,572 puntos menos en el promedio obtenido en las pruebas.

La variable que mide el sentido de pertenencia al centro educativo se basa en la pregunta: "Si te dijeran que tienes que cambiar de escuela ¿cómo te sentirías?". Los estudiantes a los que les daría alegría cambiar de centro educativo obtuvieron 23,281 puntos menos que aquellos a los que les daría mucha pena cambiar de centro educativo. Los estudiantes a los que les daría igual cambiar de centro educativo obtienen en promedio 1,367 puntos menos en las pruebas, y aquellos a los que les daría un poco de pena cambiar de centro educativo obtuvieron 6,707 puntos más que a los que les daría mucha pena (categoría de referencia).

La variable posesión de recursos de estudio integra la posesión de libros, calculadora e internet en los hogares. Los estudiantes que tienen estos tres recursos en sus hogares obtienen en promedio 16,387 puntos más que aquellos que no tienen ninguno (categoría de referencia); los estudiantes que tienen solo dos de estos recursos obtienen en promedio 12,393 puntos más, y los que tienen uno solo obtienen en promedio 1,746 puntos más en las pruebas SERCE que aquellos que no tienen ningún recurso. Estos resultados se muestran en la tabla 3.

5.2. Modelo con variables de nivel escuela

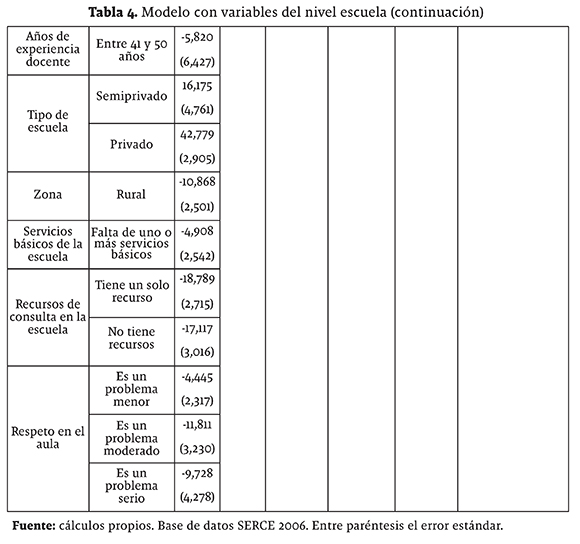
Como se observa en la tabla 4, se continúa con el modelo para mostrar el efecto de la adición de cada una de las variables del nivel escuela; se puede ver la asociación sobre la calificación SERCE 2006 en matemáticas de cada una de las variables incluidas. El mayor aporte se observa en las variables tipo de escuela y recursos de consulta en la escuela.

El coeficiente asociado a la variable sexo del profesor (β_1ijk = 4,617), tomando como categoría de base el sexo masculino, resultó positivo y estadísticamente significativo, lo que significa que los estudiantes con profesoras obtienen en promedio 4,617 puntos adicionales en comparación con los estudiantes que tienen profesores de sexo masculino.

Con respecto a la variable nivel educativo del docente que tiene como referencia la categoría técnico no universitario, se presentó un resultado inesperado, puesto que los profesores con mayor nivel educativo presentan coeficientes negativos, lo que indica que a mayor nivel educativo del profesor, los estudiantes tienen menor puntaje en matemáticas en la prueba SERCE 2006. También se observa que el mayor aporte lo realizan los profesores con nivel educativo pedagógico no universitario. Según esto, se tienen fuertes implicaciones para fortalecer la formación pedagógica de los docentes en esta área.

Al analizar el coeficiente de la variable que mide la percepción del profesor sobre falta de motivación de los estudiantes hacia las matemáticas, se observa que para los casos en los que el profesor considera un problema serio la falta de motivación, se disminuye el rendimiento en aproximadamente 5 puntos con respecto a la categoría base "es un problema menor".

El modelo muestra que existe una relación no lineal sobre la experiencia docente, dado que los docentes con experiencia menor a un año y mayor a 40 años tienen un efecto negativo sobre el rendimiento de los estudiantes. Por el contrario, se observó que entre uno y 40 años de experiencia se incrementa el rendimiento de los estudiantes en las pruebas.

Al igual que en otros estudios sobre calidad de la educación, se encontró que las escuelas públicas están en desventaja frente a las privadas, al igual que las que se encuentran en zona rural. Los estudiantes de escuela privada tienen un puntaje superior aproximadamente en 42 puntos en comparación con los estudiantes de las escuelas públicas.

Las escuelas que carecen de recursos como servicios básicos (acueducto, alcantarillado y energía) y recursos de consulta (biblioteca y sala de cómputo) se encuentran en desventaja frente a las que sí cuentan con este tipo de recursos.

El respeto en el aula de clase mide la percepción del director del centro educativo sobre el respeto que los estudiantes tienen a sus profesores. El modelo muestra que en los centros donde existe este problema de manera menor, moderada o seria, el puntaje que los estudiantes obtienen en las pruebas de matemáticas SERCE 2006 es menor en comparación a los centros educativos donde los estudiantes son respetuosos con sus profesores.

La correlación intraclase en comparación con el modelo nulo presentó una disminución de 10,9% a 9,6% en el nivel país y de 25,3% a 18,0% en el nivel escuela, lo que indica que en las pruebas SERCE 2006, del total de la varianza en el rendimiento en matemáticas para Latinoamérica, 18,0% corresponde a la variación del nivel escuela y 9,6% al nivel país; de esta forma, la inclusión de este tipo de variables asociadas a la escuela contribuye a la explicación del efecto país y del efecto escuela. Este modelo muestra que la diferenciación existente entre los puntajes que miden el rendimiento de los estudiantes en las pruebas SERCE 2006 está fuertemente influenciada por el tipo de escuela, recursos de consulta en la escuela, la zona y el respeto en el aula de clase ya que son las variables que más aportan al rendimiento.

5.3. Modelo con variables de nivel país

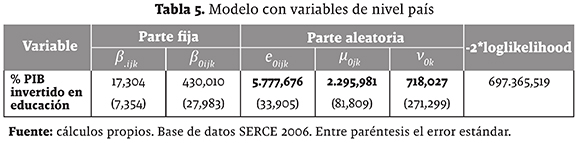
En el nivel país solamente se incluyó la variable relativa al porcentaje de PIB que cada país invierte en educación, el cual resultó significativo al comparar este modelo con el modelo nulo como se muestra en la tabla 5.

La varianza no explicada en el nivel país se reduce considerablemente en comparación con el modelo nulo, pasando de 989,181 a 718,027 lo que indica un gran aporte para tratar de explicar las diferencias de promedios entre los diferentes países participantes en la prueba. La inclusión de esta variable nos permite afirmar que por cada punto porcentual que aumente la inversión del país en educación, el rendimiento en matemáticas de los alumnos en las pruebas SERCE 2006 se vería beneficiado con un aumento de 17,304 puntos. De esta forma en los países latinoamericanos el hecho de no cumplir el compromiso de invertir un mínimo de 6% del PIB, tal y como proponía la Unesco (2000) llevaría a obtener bajos resultados, como se muestra para la mayoría de países participantes en la prueba.

5.4. Modelo total con variables de nivel alumno, escuela y país

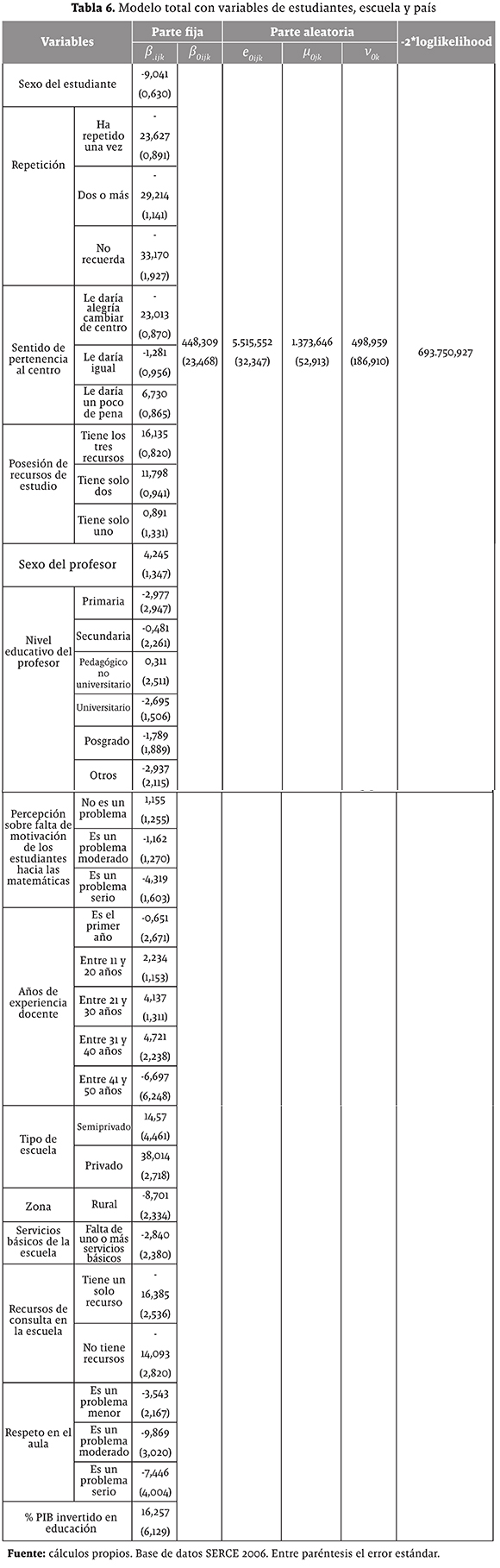
Finalmente, se quiere analizar el efecto que tienen de manera conjunta las variables de los tres niveles sobre el rendimiento en matemáticas de los estudiantes en la prueba SERCE 2006, el cual se muestra en la tabla 6.

Comparando los resultados del modelo total con respecto al modelo nulo, se puede observar en la tabla 6 que la varianza se redujo en los tres niveles; en el nivel país pasó de 989,181 a 489,296, entre escuelas pasó de 2.296,843 a 1.373,646 y entre estudiantes disminuyó de 5.776,951 a 5.515,552. El efecto conjunto de las variables de nivel alumno, escuela y país ayudan a explicar en gran proporción las diferencias interpaís, interclase e intraclase que se habían observado en el modelo nulo, debido a que la variación residual disminuyó significativamente.

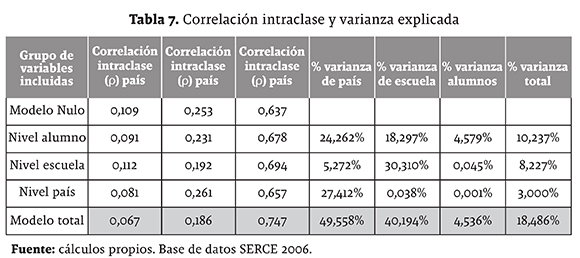
Al considerar el modelo donde solamente se incluyen variables del nivel alumno se explica 24,3% de la varianza de país, 18,3% del la varianza de las escuelas y solo 4,6% de la varianza de los alumnos. Este resultado es coherente con las correlaciones intraclase que se presentan para este caso en la tabla 7, ya que el grupo de estudiantes es muy homogéneo (ρ = 0,678) y se trata de explicar las mayores variaciones que en este caso se encuentran en las variables país y escuela.

Cuando se considera el modelo de nivel país, donde únicamente se incluye la variable porcentaje de inversión del PIB en educación, se observa que esta única variable logra explicar 27,4% de la variación del nivel. Este es un resultado muy importante porque indica que la gran heterogeneidad observada en las puntuaciones para matemáticas en SERCE 2006 entre países (ρ = 0,067) puede ser explicada en gran parte por los recursos invertidos en educación.

En el modelo total, al incluir variables de todos los niveles se explica 49,6% de la variación en el nivel país, 40,2% en el de escuela y 4,5% del nivel alumno. En general, el modelo logra explicar 18,5% de la varianza total.

La inclusión de los tres grupos de variables logró que el coeficiente de correlación intraclase en el nivel país disminuyera hasta 6,7% y en el nivel escuela a 18,6%. De esta manera, el efecto simultáneo que tienen los tres grupos de variables hacen que la variación entre los rendimientos de matemáticas en las pruebas SERCE 2006 explicada por la varianza entre los países y las escuelas se redujera, así las variaciones entre los rendimientos dependen ahora en menor medida de las diferencias observadas entre los países (efecto país) y las escuelas (efecto escuela).

Además de analizar la significación de los coeficientes, se debe analizar el ajuste global del modelo total donde se incluyen los predictores de los tres niveles. Además de ser significativo el aporte de los predictores, el modelo propuesto debe aportar información significativa en comparación con el modelo nulo. Para llevar a cabo la comparación, se hace uso de la razón de verosimilitud. El valor de -2*loglikelihood (IGLS) para el modelo total es de 693.750,927 si se compara con el valor obtenido en la estimación del modelo nulo 697.370,283, la diferencia entre ellos es de 3.619,356. Para comprobar el ajuste del modelo, se calcula la significancia de este valor con 14 grados de libertad (17 parámetros estimados en el modelo definitivo menos 4 parámetros estimados en el modelo nulo). Al obtener un valor de p = 0,000, menor que el nivel de significancia de 0,05 con el que se trabaja, así se verifica que el modelo total en general es explicativo del rendimiento en matemáticas de los alumnos en la prueba SERCE 2006.

El último paso es evaluar la calidad del mode¬lo final. Básicamente, lo que importa es conocer cuánta varianza del país, de la escuela y del alumno es explicada por el modelo. Sería un valor de su capacidad explicativa. Se estima a través del llamado coeficiente de determinación R2 (Longford 1993). Si el intercepto apenas tiene varianza aleatoria, la varianza total será la suma de las varianzas de los tres niveles. De esta forma, podremos estimar el coeficiente de determinación total R2 (pseudo R2), así como el coeficiente de de¬terminación para cada nivel con la siguiente fórmula:

Para el nivel alumno, el valor del R2 es de 4,536%, el del nivel escuela es de 40,19% y el del nivel país es 49,558%. Estos valores fueron calculados y explicados en la tabla 7.

6. Conclusiones

Se identificó un impacto fuerte de la variable sexo del estudiante sobre los resultados obtenidos en las pruebas SERCE 2006. Este efecto produce un mayor rendimiento aproximadamente en 9 puntos en el alcance de logros en matemáticas para los niños en comparación con el rendimiento logrado por las niñas, al igual que en la gran mayoría de los estudios realizados en Colombia y América Latina sobre educación básica. Es de destacar el caso de países como Costa Rica y Ecuador donde la diferencia se muestra a favor del rendimiento de las niñas.

Se evidencia una gran desventaja en el rendimiento en matemáticas de los estudiantes que presentan algún tipo de repetición en comparación con los que no repiten cursos. Cuando se analiza el clima escolar a través del sentido de pertenencia al centro educativo y el respeto en el aula, se encuentra que querer cambiar de institución disminuye el rendimiento en matemáticas aproximadamente en 23 puntos y cuando el respeto en el aula es un problema serio incide negativamente en el rendimiento. En este caso es pertinente analizar por qué a esa edad los niños no se encuentran a gusto con su institución y por qué se han perdido las normas de respeto en el aula. Esto sugiere que el Estado debe orientar una educación fundamentada en los valores humanos y mejorar la consistencia institucional de las escuelas, ya que el cambio de establecimiento educativo genera dificultades de adaptación y afecta el rendimiento académico de los niños.

El origen social de los alumnos es de mucha importancia dado que la posesión de recursos de estudio en el hogar, que puede ser tomada como una proxy del nivel socioeconómico del estudiante, tiene un efecto positivo en el alcance de logros en matemáticas en la prueba SERCE; un efecto similar se ha encontrado en varios estudios como Hanushek (2004a), Carvallo (2005), Piñeros y Rodríguez (1999) y Unesco (2008). Por tanto, los estudiantes con bajos recursos que en su mayoría se encuentran en las escuelas públicas resultan ser los más afectados.

En general, el estudio muestra que en América Latina una adecuada dotación de las escuelas, en cuanto a servicios básicos y recursos de consulta, tiene un efecto positivo y significativo sobre el rendimiento del estudiante en matemáticas; los efectos sobre el rendimiento en las pruebas SERCE son mayores en las escuelas con buenas dotaciones, de carácter privado y que se encuentren en una zona urbana.

La percepción de los profesores sobre la seriedad del problema de la falta de motivación del estudiante hacia las matemáticas incide negativamente en el rendimiento del estudiante. Lo anterior invita a realizar acciones desde el entorno familiar que motiven la preparación de los niños incluso desde una época anterior a entrar a la escuela. Además, en el sector educativo en general se debe lograr una mayor innovación en estrategias pedagógicas que busquen aumentar la motivación y el gusto por las matemáticas y la escuela para mejorar resultados, como por ejemplo integrar la comunidad latinoamericana alrededor de semilleros y olimpiadas de matemáticas de escuela primaria, que les den la oportunidad a todos los estudiantes, sin importar la región donde se encuentren, de familiarizarse con el aprendizaje de esta ciencia.

El modelo muestra que en el nivel país se encuentran resultados que concuerdan, en parte, con diferentes investigaciones sobre calidad de educación que hacen referencia al rubro de inversión en educación. El indicador del porcentaje de PIB invertido en educación por parte de cada país resultó significativo. Por cada punto adicional de inversión en el porcentaje del PIB en educación en los países aumenta el rendimiento medio esperado en matemáticas casi 17 puntos y, según lo observado, a pesar de los esfuerzos que los países latinoamericanos vienen realizando en materia de inversión se ha avanzado en cobertura educativa, pero en la mayoría de los países se pone de manifiesto que aún no se ha conseguido el compromiso de invertir mínimo 6% del PIB, tal y como propuso la Unesco en el 2000.

La inclusión de los tres grupos de variables logró que el coeficiente de correlación intraclase en comparación con el modelo nulo, en el nivel país disminuyera hasta 6,7% y en el nivel escuela a 18,6%, lo que indica el gran aporte a la explicación de la varianza entre países y escuelas. Cabe resaltar que las variables que más contribuyen son: tipo de escuela, zona, recursos de consulta, repetición de cursos, sentido de pertenencia al centro y porcentaje del PIB invertido en educación.

Para mejorar el rendimiento en matemáticas se deberían diseñar políticas que contribuyan a mejorar las condiciones de las escuelas, como por ejemplo garantizar los materiales de librería, acceso a computadores e internet tanto en escuelas como en los hogares, buenas condiciones de infraestructura y docentes calificados.

Citas de pie de página

¹ Este trabajo hizo parte del proyecto de investigación de la Convocatoria Docente Universidad del Valle, área: teoría económica y economía aplicada. Código 60-01, octubre 2013.

² Licenciado en Matemáticas. Magíster en Economía Aplicada.

Anexos

Referencias bibliográficas

Aitkin, Murray y Nicholas Longford. «Statistical Modelling Issues in School Effectiveness Studies». Journal of the Royal Statistical Society, Ser A, n° 149, 1986: 1-43.         [ Links ]

Barrera, Felipe y Alejandro Gaviria. Efficiency of Colombian Schools. Fedesarrollo, 2003. http://www.fedesarrollo.org.co/wp-content/uploads/2011/08/Efficiency-of-Colombian-Schools-fbarrera_eficiencia_escuelas.pdf (último acceso: 27 de noviembre de 2015).         [ Links ]

Bedard, Kelly y Elizabeth Dhuey. «The Persistence of Early Childhood Maturity: International Evidence of Long-Run Age Effects». The Quarterly Journal of Economics, Vol. 121, n° 4, 2006: 1.437-1.472.         [ Links ]

Bowles, Samuel y Henry Levin. «The Determinants of Scholastic Achievement. An Appraisal of Some Recent Evidence». Journal of Human Resources, Vol. 3, 1968: 3-24.         [ Links ]

Bryk, Anthony y Stephen Raudenbush. Hierarchical Linear Models. Applications and Data Analysis Methods. Newbury Park, CA: SAGE, 1992.         [ Links ]

Carvallo, Mauricio. «Análisis de los resultados obtenidos en estudios de eficacia escolar en México, comparados con los de otros países». Revista Electrónica Iberoamericana sobre Calidad, Eficacia y Cambio en Educación, Vol. 3, n° 2, 2005: 80-108.         [ Links ]

Cervini, Rubén. «Nivel y variación de la equidad en la educación media en Argentina». Revista Iberoamericana de Educación, Vol. 4, n° 34, 2004: 1-19.         [ Links ]

Coleman, James. Equality of Educational Opportunity. Washington, D.C.: U.S. Department of Education, 1966.         [ Links ]

Concha, Carlos. «Estudio de 32 escuelas de alta vulnerabilidad socio-económica y altos resultados de aprendizaje». En Estudios sobre eficacia escolar en Iberoamérica. 15 buenas investigaciones, coordinado por Javier Murillo, 83-110. Bogotá: Convenio Andrés Bello, 2006.         [ Links ]

Coombs, Philip y Jacques Hallak. Cost Analysis in Education: A Tool for Policy and Planning. Baltimore y Londres: The John Hopkins University Press, 1987.         [ Links ]

Cueto, Santiago y Walter Secada. «Oportunidades de aprendizaje y rendimiento en matemática de niños y niñas aimara, quechua y castellano hablantes en escuelas bilingües y monolingües en Puno, Perú». En Etnicidad, raza, género y educación en América Latina, editado por Donald Winkler y Santiago Cueto, 315-354. Washington D.C.: PREAL, 2004.         [ Links ]

Delprato, Marcos. «Determinantes del rendimiento educativo del nivel primario aplicando la técnica de análisis multinivel». Instituto de Estudios sobre la Realidad Argentina y Latinoamericana (IERAL), Documento de Trabajo, n° 27, 1999: 1-137.         [ Links ]

Fuentes, Raúl, Héctor Ortiz, Jaime Valenzuela y Víctor Vilos. «Estudio internacional de las escuelas eficaces en Chile y Guatemala para la formulación de una propuesta educativa en mejoramiento de la calidad de la educación». En Estudios sobre eficacia escolar en Iberoamérica. 15 buenas investigaciones, coordinado por Javier Murillo, 167-196. Bogotá: Convenio Andrés Bello, 2006.         [ Links ]

Gaviria, Alejandro y Jorge Barrientos. «Determinantes de la calidad de la educación en Colombia». Archivos de Economía (Departamento Nacional de Planeación), n° 159 (noviembre 2001): 1- 88.         [ Links ]

Gaviria, José y María Castro. Modelos jerárquicos lineales, Cuadernos de Estadística No. 29. Madrid: Editorial La Muralla S.A., 2005.         [ Links ]

Gelman, Andrew y Jennifer Hill. Data Analysis Using Regression and Multilevel/Hierarchical Models. Cambridge: Cambridge University Press, 2006.         [ Links ]

Goldstein, Harvey. «Methods in School Effectiveness Research». School Effectiveness and School Improvement, Vol. 8, n° 4, 1997: 69-395.         [ Links ]

Goldstein, Harvey. Multilevel Statistical Models. Nueva York: Arnold, 2003.         [ Links ]

Goldstein, Harvey, Jhon Rabash, Fiona Steele, William Browne, Bob Prosser y Michael Healy. A User's Guide to MLwiN. Londres: Centre for Multilevel Modelling Institute of Education University of London, 2004.         [ Links ]

Greenberg, Evans. 2004. Climates for Learning. Presentación ante la reunión anual de la "American Educational Research Association", San Diego, CA, 12-16 de abril de 2004.         [ Links ]

Hanushek, Eric. «The Production of Education, Teacher Quality, and Efficiency». En U.S. Office of Education, Do Teachers Make a Difference?,  79-99. Washington, D.C.: Government Printing Office, 1970.         [ Links ]

Hanushek, Eric. «What if There Are no Best Practices?». Scottish Journal of Political Economy, Vol. 51, n° 2, 2004a: 156-172.         [ Links ]

Hanushek, Eric. «United States Lessons about School Accountability». Journal for Institutional Comparisons (Center for Economic Studies and Ifo Institute of Economic Research, Munich), Vol. 2, n° 4, 2004b: 27-32.         [ Links ]

Hanushek, Eric y Javier Luque. «Efficiency and Equity in Schools around the World». Economics of Education Review. Vol. 22, n° 5, 2003: 481-502.         [ Links ]

Hanushek, Eric y Ludger Woessmann. Education Quality and Economic Growth. Washington D.C.: Banco Mundial, 2007.         [ Links ]

Heck, Ronald y Scott Thomas. An Introduction to Multilevel Modeling Techniques. Hillsdale, NJ: Lawrence Erlbaum Associates, 2000.         [ Links ]

Hox, Joop. Applied Multilevel Analysis. Amsterdam: TT-Publikaties, 1995.         [ Links ]

Hox, Joop y Edith De Leeuw. Assumptions, Robustness, and Estimation Methods in Multivariate Modeling. Amsterdam: TT-Publikaties, 1998.         [ Links ]

Iregui, Ana, Ligia Melo y Jorge Ramos. «Evaluación y análisis de eficiencia de la educación en Colombia». Borradores de Economía (Banco de La República), n° 381, 2006: 1-105.         [ Links ]

Lee, Jong-Wook y Robert Barro. «Schooling Quality in a Cross-Section of Countries». Economica, Vol. 68, n° 272, 2001: 465-488.         [ Links ]

Levin, Hank. Cost-Effectiveness. Nueva York: Sage Publications, 1983.         [ Links ]

Longford, Nicholas. Random Coefficient Models. Oxford: Oxford University Press, 1993.         [ Links ]

Mizala, Alejandra, Pilar Romaguera y Teresa Reinaga. «Determinantes del rendimiento escolar en Bolivia: análisis de las pruebas SIMECAL». En Estudios sobre eficacia escolar en Iberoamérica. 15 buenas investigaciones, coordinado por Javier Murillo, 287-314. Bogotá: Convenio Andrés Bello, 2006.         [ Links ]

Monette, Georges, Qing Shao y Ernest Kwan. «A First Look at Multilevel Models». Institute for Social Research Statistical Consulting Service, York University (octubre-noviembre 2001): 1-96.         [ Links ]

Murillo, Francisco. «Un estudio multinivel sobre los efectos escolares y los factores de eficacia de los centros docentes de primaria en España». En Estudios sobre eficacia escolar en Iberoamérica. 15 buenas investigaciones, coordinado por Javier Murillo, 345-372. Bogotá: Convenio Andrés Bello, 2006.         [ Links ]

Murillo, Francisco y Marcela Román. «¿La escuela o la cuna? Evidencias sobre su aportación al rendimiento de los estudiantes de América Latina. Estudio multinivel sobre la estimación de los efectos escolares». Profesorado. Revista de Curriculum y Formación de Profesorado, Vol. 15, n° 3, 2011: 27-53.         [ Links ]

Piñeros, Luis y Alberto Rodríguez. «School Inputs in Secondary Education and their Effects on Academic Achievement: A Study in Colombia». LCSHD Paper Series (World Bank Human Development Department), n° 36, 1999: 1-60.         [ Links ]

Rodríguez, Juan, Heater Simpson y Corg Heyman. Usos y necesidades de información sobre calidad para la gerencia educativa en el Salvador. San Salvador: Ministerio de Educación, Gobierno de El Salvador, USAID, 2004. http://pdf.usaid.gov/pdf_docs/PNADE126.pdf (ültimo acceso: 10 de noviembre de 2015).         [ Links ]

Rowe, Kenneth, Peter Hill y Philip Holmes-Smith. «Methodological Issues in Educational Performance and School Effectiveness Research: A Discussion with Worked Examples». Australian Journal of Education, Vol. 39, n° 3, 1995: 217-248.         [ Links ]

Unesco. World Declaration on Education for all and Framework for Action to Meet Basic Learning Needs. Nueva York: Unesco, 1990.         [ Links ]

Unesco. Marco de Acción de Dakar. Educación para Todos: cumplir nuestros compromisos comunes. Adoptado en el Foro Mundial sobre la Educación, Dakar (Senegal). París: Unesco, 2000. http://unesdoc.unesco.org/images/0012/001211/121147s.pdf (último acceso: 13 de octubre de 2014).         [ Links ]

Unesco. Los aprendizajes de los estudiantes de América Latina y el Caribe. Primer reporte del SERCE 2006. Santiago de Chile: Unesco, 2008.         [ Links ]

Vegas, Emiliana y Jenny Petrow. Raising Student Achievement in Latin America: The Challenge for the 21st Century. Washington, D.C.: Latin American Development Forum, Banco Mundial, 2007.         [ Links ]

Wenglinsky, Harold. School District Expenditures, School Resources and Student Achievement: Modeling the Production Function. Washington, D.C.: Education Testing Service, 1998.         [ Links ]

Woessmann, Ludger. «Schooling Resources, Educational Institutions and Student Performance: The International Evidence». Oxford Bulletin of Economics and Statistics, Vol. 65, n° 2, 2003: 117-170.         [ Links ]

Zambrano, Juan. «Análisis multinivel del rendimiento escolar en matemáticas para grado cuarto de educación básica primaria en Colombia». Sociedad y economía, n° 25, 2013: 205-236.         [ Links ]

Este trabajo está bajo la licencia Creative Commons Attribution 3.0

¿Cómo citar este artículo? / How to quote this article?
Zambrano, Juan. «Un estudio multinivel del rendimiento escolar en matemáticas para tercer grado de educación básica primaria en América Latina». Sociedad y economía, No. 30 (enero - junio 2016): 91-120.