Análisis comparativo de modelos hidrodinámicos y cinéticos para fotobiorreactores airlift

Comparative analysis and kinetic model for photobioreactors
hydrodynamic airlift

Félix Fabián Cortés Conde¹, Diego Rubio Fernández², Édisson Mateo Gómez Espinosa³

1 Ingeniero Químico, Investigador Grupo BIOTECNOLOGíA. Fundación Universidad de América. Bogotá D.C, Colombia. Fabiancortes1488@gmail.com.
2 MSc. en Ciencias, Universidad Nacional de Colombia. Docente Tiempo Completo, Investigador Grupo BIOTECNOLOGíA, Fundación Universidad de América. Bogotá D.C, Colombia. diegrubio@gmail.com.
3 Ingeniero Químico, Investigador Grupo BIOTECNOLOGíA. Fundación Universidad de América. Bogotá D.C, Colombia. mateo.gomez.espinosa@gmail.com.

RESUMEN

En las últimas décadas se han investigado nuevas fuentes de energía renovable, siendo las microalgas una de las preferidas, debido a su alta producción de biomasa, utilizada en la elaboración de biocombustibles de segunda generación como bioetanol, biohidrógeno y biodiesel. Las microalgas se cultivan en recipientes especializados llamados reactores, en los cuales se controlan las condiciones de cultivo para obtener la máxima producción de biomasa. A partir de datos experimentales se han generado modelos matemáticos, que predicen el comportamiento que ocurre en el interior de los biorreactores, para realizar mejoras en el diseño y predecir las condiciones óptimas del cultivo y obtener una buena productividad. Se analizaron modelos hidrodinámicos de tres fases para establecer cuál de los modelos analizados predice de manera eficiente el comportamiento hidrodinámico a lo largo del biorreactor. Posteriormente se analizaron modelos de crecimiento de microorganismos fotosintetisantes en fotobiorreactores para acoplar el crecimiento de las microalgas a la hidrodinámica desarrollada en la primera parte de la investigación y concluir con la simulación de un fotobiorreactor tipo Airlift.

PALABRAS CLAVE: Biorreactores Airlift, Hidrodinámica, Fotobiorreactor, Microalgas, Simulación.

ABSTRACT

In recent decades new sources of renewable energy has been investigated, being algae a favorite because of its high biomass production, used in the development of second generation biofuels as bioethanol, biohydrogen and biodiesel. The algae are grown in specialized containers called reactors, which controls the culture conditions for maximum production of biomass. From experimental data were generated mathematical models, which predict the behavior that occurs inside the bioreactor, for improvements in the design and predict the optimum conditions of culture to obtain a good productivity. Three phase hydrodynamic models were analyzed in order to establish which model predicts efficiently hydrodynamic behavior along the bioreactor. Then models of growth of microorganism in photobioreactors for coupling the growth of microalgae to hydrodynamics developed in the first part of the research and conclude with a simulation of the Airlift photobioreactor.

KEYWORDS: Airlift Bioreactors, hydrodynamic, microalgae, photobioreactor, simulation.

1. INTRODUCCIÓN

Las microalgas tienen un gran potencial biotecnológico para la producción de sustancias valiosas, utilizadas principalmente en las industrias farmacéuticas, cosméticas y de biocombustibles, la última es la de mayor interés en investigaciones recientemente, debido a que presenta una fuente de energía renovable ambientalmente amigable en comparación con las energía tradicionales que se han empleado en las últimas décadas tales como el carbón y el petróleo [1] [2].

Para el cultivo de las microalgas existen equipos especializados llamados reactores los cuales pueden dividirse en reactores agitados mecánicamente y reactores agitados neumáticamente, entre los agitados mecánicamente se encuentran el reactor Batch, y en los agitados neumáticamente están la columna de burbujeo y el Reactor Airlift (ALR). Se considera que el reactor Airlift es uno de los más utilizados, por sus claras ventajas frente a otros reactores, entre las cuales están una mejor capacidad de transferencia de masa, mayores velocidades superficiales gas-líquido, se puede conseguir patrones de flujo bien definidos, mejor rentabilidad, mínimo riesgo de contaminación, posibilidad simple y altamente efectiva de fluidización de los sólidos generación de esfuerzos cortantes bajos y uniformes lo que ayuda al crecimiento celular sin dañar o estresar al microorganismo.[3][4].

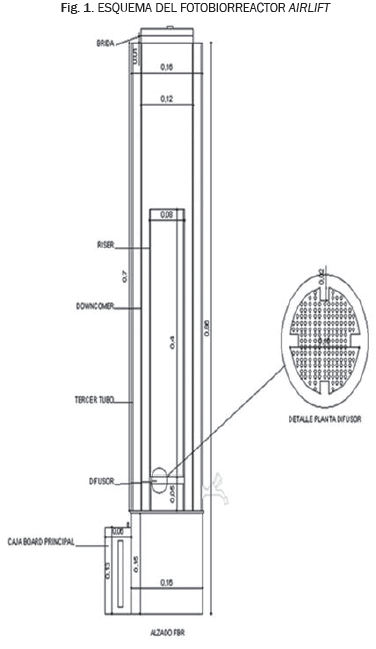
Los Reactores Airlift (ALR) se dividen en cuatro secciones bien definidas que son: el Top, la base, el Dowcomer o canal de descenso y el Riser o canal de ascenso como se presenta en la Fig. 1.

Además existen parámetros que se deben tener en cuenta para comprender los fenómenos hidrodinámicos que ocurren en el interior del fotobiorreactor como son: la velocidad del líquido, la velocidad del gas Holdup (Retención del gas) y la velocidad del sólido cuando se tiene en cuenta una tercera fase. Por otra parte en las últimas décadas se han utilizado software de tipo comercial para la simulación de procesos químicos, debido a sus claras ventajas frente a los datos experimentales, uno de estos factores es la reducción de costos a la hora de encontrar soluciones a problemas de procesos de producción; en este caso al cultivo de microalgas para fotobiorreactores [5] [6] [7].

El objetivo de este artículo es establecer el mejor modelo, que prediga el comportamiento en el interior de un fotobiorreactor Airlift, específicamente; la hidrodinámica y la tasa de crecimiento. Para esto se analizaron tres modelos hidrodinámicos para sistemas de tres fases y dos modelos cinéticos para el crecimiento de las microalgas y se acoplaron estos dos fenómenos para concluir la simulación del fotobiorreactor Airlift.

II. DESARROLLO DEL ARTÍCULO

Simulación de reactores Airlift de tres fases gas-líquido-sólido Muchos autores explican el comportamiento hidrodinámico de los sistemas Airlift de tres fases a partir de modelos hidrodinámicos de dos fases. Los modelos propuestos por Livingston y Wen-Jang se basaron en el modelo predictivo de Chisti (1988) para determinar la velocidad de circulación interna del líquido en el Riser y Downcomer utilizado "(1)", y asumida la fase líquida y la fase sólida como una fase seudo-homogénea. Para ello es necesario considerar que la densidad media de la fase líquida y la fase sólida es uniforme a lo largo de todo el reactor.

Donde ε_R y ε_D son las retenciones del gas en el Riser y Downcomer, respectivamente.

Sin embargo, el modelo hidrodinámico de tres fases propuesto por García Calvo se desarrolla a partir de balances de energía para determinar la disipación energética producida por la interacción de la fase gaseosa con la fase líquida y las pérdidas de fricción producidas por la interacción del sólido con las paredes del reactor. Los parámetros más importantes para caracterizar la dinámica de fluidos en los reactores de tres fases son la retención del gas en el canal de ascenso y descenso, la velocidad de circulación del líquido en el canal de descenso y la distribución de los sólidos, debido a que el modelo propuesto por García Calvo es pertinente mantener una velocidad de gas crítica para conservar una suspensión homogénea de los sólidos dentro del reactor [8].

A. Modelo hidrodinámico propuesto por Livingston y Zhang para sistemas de tres fases

Este modelo considera que un sistema Airlift de tres fases consta de dos secciones transversales, una determinada por el Riser y la otra por la base o cima del ALR . Debido a la diferencia de secciones entre estas dos zonas, las velocidades de arrastre del líquido son diferentes en cada una de ellas, lo que provoca distintas densidades efectivas en la mezcla líquido-sólido [9].

Como en muchos modelos para sistemas bifásicos, la expresión matemática del modelo se obtiene al identificr las pérdidas de energía debido a la fricción que ejerce el líquido con las paredes del reactor y a la energía de disipación provocada en la interfase gas-líquido.

El modelo propuesto por Livingston (1993) es una extensión del modelo propuesto por Chisti (1988) expuesto en "(1)", donde se le añaden variables influyentes tales como la retención del sólido, la densidad de la fase seudo-homogénea, la viscosidad de la fase seudo-homogénea y la fracción de sólido en el tubo ya que estas corrigen el efecto de la presencia de la tercera fase sólida en el tanque. Las ecuaciones que modifican el modelo de Chisti son:

Donde ε_R y ε_D son las retenciones del gas en el Riser y Downcomer, respectivamente, ε_SR y ε_SD son las retenciones del sólido en el Riser y Downcomer, respectivamente.

B. Modelo hidrodinámico propuesto por Wen-Jang Lu y Shyh-Jye Hwang para sistemas de tres fases con partículas de baja densidad y carga de sólidos (1994)

El modelo matemático propuesto por Wen-Jang y Shyh Hwang proponen un modelo predictivo para calcular la retención de los sólidos y la velocidad de circulación del líquido considerada la formación de una fase seudo homogénea entre la fase sólida y la fase líquida. Al realizar los balances de energía en las diferentes zonas del reactor (Canal de ascenso y canal de descenso) se obtiene la expresión general para calcular la velocidad de circulación del líquido en el Downcomer, consideradas las pérdidas de fricción provocadas por las interacción del sólidos con las paredes del sistema y las pérdidas de energía provocadas por expansión isotérmica del gas en el líquido [10] [11].

Donde los coeficientes K_T y K_B son los coeficientes de pérdida por fricción en la cima y base del reactor, respectivamente, y las constantes de fricción en el Riser y en el Downcomer K_R y K_B, se calculan por medio "(6)" y "(7)".

Donde f es el factor de fricción, L_R y L_D son las longitudes del Riser y Downcomer, respectivamente, d_R y d_D son los diámetros del Riser y Downcomer, respectivamente.

Al interactuar la fase líquida y la fase sólida en el ALR , las propiedades reológicas del fluido como la densidad y la viscosidad se ven afectadas al formar una fase seudo-homogénea dentro del reactor. Para esto es necesario calcular la densidad de la fase seudo-homogénea mediante "(8)" y la viscosidad de la fase seudo-homogénea con "(9)", la cual es una correlación propuesta por Oliver (1961):

• Densidad de la fase seudo-homogénea



• Viscosidad (correlación propuesta por Oliver (1961)

C. Modelo hidrodinámico para sistemas de tres fases con altas cargas de sólidos para los ALR propuesto por García Calvo (1999)

El modelo propuesto por García Calvo describe el comportamiento hidrodinámico en tres fases (sólido-líquido-gas) para reactores Airlift. Fue desarrollado a partir de balances de energía donde se tienen en cuenta la disipación de energía en la interfase gas-líquido y las pérdidas de energía debido a la fricción entre el sólido y las paredes del sistema. El modelo predice la velocidad de circulación del líquido y del sólido, la retención del gas y la distribución de los sólidos dentro del reactor [12].

Para desarrollar el modelo es necesario establecer las siguientes características:

• El balance asume diferentes fases seudo-homogéneas tanto en el Riser como en el Downcomer, para esto es necesario tener en cuenta las diferentes concentraciones de sólidos en ambas secciones del reactor.
• La densidad del Downcomer es igual a la densidad del líquido, ya que todas las partículas sólidas están el Riser.
• El modelo no asume la presencia de gas en el Downcomer, se considera el comportamiento de gas en el Riser similar al de una columna de burbujeo (U_D(1-ε_SD)=u_LD)

1) Balance de energía planteado por García Calvo (1988)

Dado que al mantener una fase solida suspendida en el reactor, la combinación entre la fase sólida y la fase líquida genera una fase seudo-homogénea donde es necesario calcular la densidad de la mezcla por medio de "(11)" y "(12)".

D. Simulación de la parte biológica del fotobiorreactor

Para la determinación de la tasa de crecimiento de las microalgas en el reactor, se investigó sobre modelos que predicen el crecimiento a partir de expresiones matemáticas, los cuales tienen en cuenta fenómenos como son; la fotosíntesis, la irradiación, los ciclos de luz y oscuridad, la eficiencia cuántica, la concentración de nutrientes. De los modelos estudiados se seleccionó dos modelos específicamente para determinar el crecimiento de las microalgas en los fotobiorreactores, debido a la cantidad de modelos existentes en la literatura, uno de ellos es el modelo de Molina Grima (1994) y el otro Wu y Merchuck (2001), los cuales predicen eficientemente el comportamiento de las microalgas "Isochrysis galbana" y "Porphyridium Sp" respectivamente.

III. ANÁLISIS DE RESULTADOS

Para analizar el comportamiento hidrodinámico del fotobiorreactor Airlift fue necesario realizar la comparación de los modelos propuestos por Livingston (1993), Wen-Jang (1994) y García Calvo (1999), donde se observó que los modelos de Livingston y Wen-Jang son predictivos para densidades y concentraciones de sólidos bajas, debido a que necesita grandes cantidades de gas para mantener una distribución homogénea del sólido y no obstruya la entrada de gas en la base del reactor. Sin embargo, al ser extensiones del modelo bifásico de Chisti, los modelos de Livingston y Wen-Jang son poco predictivos ya que ignoran las condiciones en las que se producen los atascos en los reactores Airlift.

Al desarrollar el modelo hidrodinámico planteado por García Calvo, se observó que el modelo es capaz de determinar los diferentes regímenes de flujo y soporta grandes cargas de sólidos, pues necesita pequeñas cantidades de gas para mantener una distribución de sólidos dentro del reactor.

Para interpretar la hidrodinámica en un Fotobiorreactor Airlift es necesario calcular la retención del sólido y la distribución de los sólidos en un sistema inorgánico, como las perlas de vidrio, para entender cómo es el comportamiento del reactor Airlift con una tercera fase que circula en el interior y de cómo se afecta la velocidad del líquido y de gas en las diferentes zonas del reactor.

El método iterativo utilizado para la resolución del problema fue un Newton Raphson Multivariable para calcular la velocidad superficial del líquido en el Downcomer, la velocidad lineal del líquido cuando R=0 y la retención del gas en el Riser. Para desarrollar el modelo propuesto por García Calvo (1999) fue necesario utilizar las correlaciones de Koide (1984) para determinar la velocidad de sedimentación de la partícula al emplear como medio sólido las perlas de vidrio con diámetros de partícula de 1.5 y 3.5mm para mantener una buena distribución de los sólidos dentro del TP - ALR (Reactor Airlift de tres fases).

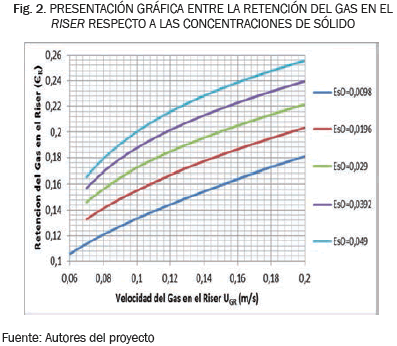
La Fig. 2 presenta la relación entre la concentración del sólido respecto a la retención del gas en el Riser; se observa que al aumentar el caudal de gas la retención del gas en el Riser aumentan, debido a que se generan una mayor cantidad de burbujas las cuales adquieren movimientos oscilatorios que provocan un régimen turbulento, indicado para romper las burbujas, pues maximiza de esta manera la transferencia de masa entre la fase gaseosa y líquida, y genera un mezclado homogéneo de gas en el reactor.

E. Modelo de Molina Grima (1994)

Se basó en una parte experimental y una parte teórica, este modelo predice de manera satisfactoria la tasa de crecimiento de organismos fotosintéticos, debido a que incluye un factor determinante como es la concentración de luz, presente en el interior del fotobiorreactor. Se toman como variables dependientes de la luz; el ángulo de incidencia y la distancia recorrida [13].

El modelo también tiene en cuenta la concentración de biomasa presente en el biorreactor, ya que al aumentar de manera acelerada se puede presentar el fenómeno de atenuación de la luz. La ventaja de este modelo comparado con los otros modelos, es que incluye una parte experimental, la cual se utiliza para calcular las constantes que se puede emplear para cada especie de microalgas y por consiguiente, la simulación del crecimiento.

Al realizar la simulación se obtuvo la Fig. 3, donde se presenta la cantidad de luz incidente en el interior del reactor, utilizado el modelo propuesto por Ever (1990) [14] en el cual pone como variable dependiente el ángulo de incidencia, vemos cómo al aumentar la distancia de penetración de la luz al interior del reactor se presenta el fenómeno de atenuación de la luz. Por consiguiente, en el interior del reactor tan sólo el 61% de la cantidad de luz total llega a este punto presentándose, de esta manera, intervalos de tiempo con alta intensidad y baja intensidad de luz, que hacen que se presenten ciclos de luz y oscuridad.

Al presentarse estos ciclos de luz y oscuridad se evita la foto-inhibición celular que es uno de los fenómenos que se desea evitar, debido a que ocasiona el estancamiento del crecimiento y en algunos casos la muerte celular.

La Fig. 4 representa el crecimiento celular, cuando el cultivo está expuesto a ciertas cantidades de luz expresadas en cuantos de energía, esta curva permite determinar la cantidad de luz necesaria, para tener el crecimiento máximo de las microalgas y de esta manera obtener una productividad alta en el interior del fotobiorreactor.

F. Modelo de Wu y Merchuck (2001))

Se basó principalmente en los supuestos de Eilers y Peeters (1988) [15]; consiste en el supuesto de centros activos que son estados celulares según la capacidad de absorción de fotones; al conjunto de los estados se les denomina como Fábrica Fotosintética PSF y es considerada como uno de los conceptos más importantes para relacionar la irradiación, la dinámica de fluidos y la cantidad de biomasa producida. Estos tres estados se presentan en la Fig. 5; el primero X₁ o fase abierta, cuando el PSF se encuentra libre de fotones y apto para recibir fotones; el segundo X₂ o fase activa, cuando él PSF es activado por la absorción de un fotón; y, por último, X₃ o estado foto-inhibido cuando hay un exceso en el número de fotones presentes en el PSF que ocasionan foto-inhibición [16].

Este modelo tiene en cuenta la interacción de variables importantes como son: la disponibilidad de la luz, el proceso de fotosíntesis, la fotoinhibición y la dinámica de fluidos.

En la Fig. 6 se puede observar, como la tasa de crecimiento es afectada por la cantidad de PFD o Photon Flux Density que es una medida de la cantidad de irradiación lumínica que alcanza el cultivo. Tomando como referencia un tiempo de luz de 45 segundos, se observa que a valores bajos de PFD , el crecimiento es negativo debido a que no existe suficiente energía que supla las necesidades básicas de las microalgas. Por consiguiente, la producción de biomasa es baja. Cuando el valor de irradiación PFD está entre los 550 y 1000 PFD, existe un crecimiento positivo, en el cual se ve beneficiada la duplicación celular, pero cuando excede estos valores, se presenta el factor de foto inhibición como se ve en la curva con 2000 PFD. Este aspecto también ha sido relacionado con aspectos de la geometría de los fotobiorreactores Airlift y tubulares, y se ha constituido en un aspecto importante para su diseño y modelamiento.

Al comparar los dos modelos de crecimiento específicos para fotobiorreactores, se tomaron como criterios de selección la variedad de microalgas de cultivo, el desarrollo matemático, el porcentaje de error, variables de entrada, variables de estado y variables de salida. El modelo de Molina Grima (1994) tiene ventajas sobre el modelo de Wu y Merchuck (2001), debido a que el modelo de Molina Grima (1994) puede predecir el crecimiento para cualquier clase de microalgas, por la utilización de un cálculo experimental, el desarrollo matemático es sencillo y no se requiere determinar valores difíciles experimentales para su parametrización, su porcentaje de error no supera el 10% y otra clara ventaja es la poca cantidad de variables de entrada, estado y salida, este modelo es la mejor opción para predecir el crecimiento en el interior del fotobiorreactor.

G. Simulación hidrodinámica de un Fotobiorreactor Airlift

Para desarrollar el modelamiento hidrodinámico de un Fotobiorreactor Airlift se utilizó el modelo propuesto por García Calvo (1999) para el sistema de tres fases (sólido, líquido, gas) en los Reactores Airlift. Este modelo es una extensión del modelo de dos fases propuesto por García Calvo (1989). Este se desarrolló a partir de balances de energía para determinar la energía de disipación en la interfase gas-líquido y las pérdidas por fricción que ejerce el fluido con las paredes del sistema. Los parámetros hidrodinámicos más importantes para predecir el modelo son: la velocidad de circulación del líquido y del sólido, la retención del gas y la distribución de los sólidos dentro del reactor. Este modelo es el más completo en comparación con otros reportados en la literatura, ya que es el único capaz de identificar las fronteras entre los diferentes regímenes de flujo y soporta grandes cargas de sólidos, al obtener un aumento en la producción de biomasa requerida para la extracción de lípidos u otras moléculas de alto valor agregado.

Para predecir el comportamiento de cultivo de microalgas en un reactor Airlift, es necesario determinar los parámetros hidrodinámicos más importantes para mantener un ambiente óptimo para la producción de biomasa, estos parámetros son: la retención del sólido en el Riser y Downcomer, la retención del gas en el Riser y la velocidad superficial del líquido en el Downcomer.

En el caso de cultivos microalgales los IL-ALR (Reactores Airlift de Lazo Interno) proporcionan las condiciones necesarias para que las células fotosintéticas puedan desarrollarse a partir de una exposición adecuada de luz, facilita la absorción de nutrientes debido al mezclado homogéneo que produce la interacción del gas con la fase líquida, produce bajos esfuerzos de corte originado por el movimiento oscilatorio producido por la agitación del líquido.

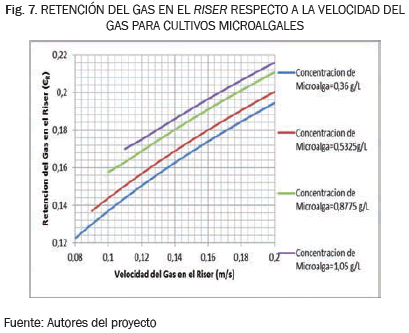
La Fig. 7 presenta la variación entre la velocidad del gas en el Riser, la concentración de biomasa producida por la microalga y la retención del gas en el Riser, se demuestra que al aumentar el caudal de gas y la concentración de biomasa, la retención de gas en el Riser aumenta debido a que se genera una mayor cantidad de burbujas, las cuales son las encargadas de incrementar la concentración de gas en la fase líquida, para generar una mayor producción de biomasa, debido a que el microorganismo tiene una mayor facilidad de encontrar los nutrientes suspendidos en el líquido provocado por el flujo heterogéneo.

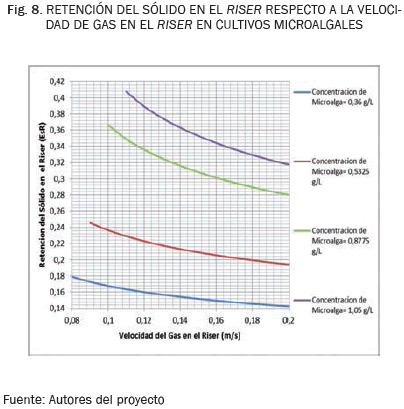
Analizado el comportamiento como se observa en la Fig. 8, la retención del sólido en el Riser en función de la velocidad del gas en el Riser, es preciso demostrar que al aumentar la velocidad del gas, la retención del sólido disminuye ya que al aumentar la velocidad del líquido en el Riser, la remoción del sólido suspendido es mayor, ya que el flujo líquido se lleva el sólido hacia el Downcomer, para dar como resultado una mayor distribución de los sólidos y aumentar, de esta manera, el área de flujo entre la fase sólida y la fase líquida. Gracias a esto la velocidad de salida del líquido en el Riser aumenta al maximizar la transferencia de masa entre la fase gaseosa y la fase líquida y provocar un mezclado homogéneo dentro del reactor.

IV. CONCLUCIONES

Los modelos de crecimiento de microalgas se basan en expresiones matemáticas complejas, que simulan el crecimiento del cultivo a partir de procesos matemáticos y tiene como principal variable la luz en el caso de cultivos de tipo fotoautotrófico o fotoheterotrófico, debido a que este es el principal factor que limita el crecimiento de las microalgas. Por consiguiente, los modelos simulan el crecimiento y controlan las variables de estado como: temperatura, pH, concentración de nutrientes y concentración de luz que existe en el medio de cultivo.

Para obtener una mayor productividad en fotobiorreactores se debe considerar los siguientes aspectos:

• Hidrodinámica: determina los patrones de flujo del sistema; se prefiere un régimen turbulento, que permite un mezclado más homogéneo del sistema, lo cual mejora la transferencia de masa y facilita, de esta manera, la absorción de nutrientes y de energía lumínica en el sistema.
• Irradiación: la calidad y cantidad de la irradiación más específicamente entre longitudes de onda entre 400 - 700nm(PAR) y 1000 µE/m²s PFD, estos valores varían con respecto a la especie de microorganismo, permiten una eficiencia cuántica cercana a 1, que es la óptima para el proceso de fotosíntesis, se evita, de esta manera, el proceso de fotoinhibición (destrucción de las proteínas de la membrana celular) e incrementar así la duplicación celular.
• Distribución de la luz: es un parámetro difícil de controlar debido a la complejidad del fenómeno de la luz; ya que vincula muchos factores como: ángulo de incidencia, cantidad de PFD, efectos de refracción, propagación y difracción, atenuación de la luz debido a la concentración de Biomasa, Fuentes de luz, reflexión y dispersión y Fotoquímica.

Apéndice: Unidades del sistema MKSA

La Tabla. I, presenta las abreviaturas de los modelos hidrodinámicos y de los modelos cinéticos utilizados en el Fotobiorreactor Airlift:

Tabla I

AGRADECIMIENTOS

Los autores reconocen y agradecen todo el apoyo, conocimiento y tiempo brindado por el departamento de investigación de la Fundación Universidad de América, nuestro director Diego Rubio, el Ingeniero Juan Sandoval y el Ingeniero Jaime Arturo Calvache, quienes fueron el soporte a lo largo de este trabajo. A todas las personas especialmente a la profesora Colombia Vivas, que formó parte del proceso y desarrollo de este trabajo con su talento humano y solidaridad, brindándonos generosamente su conocimiento y experiencia.

REFERENCIAS

[1] M.Y Chistl, Airlift Bioreactors, Applied Elsevier Science, U.S.A, 1989.         [ Links ]

[2] Wang Si-Jing y Zhong Jian J. Bioreactor Engineering, Bioprocessing for Value-Added Products from Renewable Resources, 1st. Ed, Elsevier Science. p. 161-170. 2007.         [ Links ]

[3] Y. Chisti y M. Moo-young, Bioreactor, Encyclopedia of Physical Science and Technology. 3 Ed., Elsevier Science. p. 248-255. 2002.         [ Links ]

[4] Huérfano, Guillermo, Diseño y Simulación de un Reactor Airlift para la Producción de Alcohol Etílico con ---Saccharomyces Cerevisiae Utilizando Solanum Tuberosum, Bogotá, Tesis Ingeniería Química, Universidad de América, Facultad de Ingeniería, Departamento de Ingeniería Química, 2009.         [ Links ]

[5] Arturo Calvache, Jaime A, Simulación de Bioreactores Airlift, Tesis de Maestría, Facultad de Ingeniería Química, Universidad Nacional de Colombia, 2002.         [ Links ]

[6] Merchuck, J.C, Bioreactor Airlift Reactor. Encyclopedia of Bioprocess Technology. 2002.         [ Links ]

[7] Merchuck, J.C, y Siegel M.H., Air-Lift Reactors in Chemical and Biological Technology, Journal of Chemical Technology and Biotechnology, Vol. 41, No 2, pp. 105-120. 1988.         [ Links ]

[8] García, E. Rodríguez A., A Fluid Dynamic Model for Three-Phase Airlift Reactors, Chemical Engineering Science, vol. 54, pp. 2359-2370. 1999.         [ Links ]

[9] Díaz, Ricardo M, Estudio del Flujo en Reactores con Tres Fases por Simulación, Tesis Doctoral, Facultad de Ciencias Químicas, Departamento de Ciencia de los Materiales e Ingeniería Metalúrgica, Madrid, 2001.         [ Links ]

[10] Hwang, S. J. y Wen, J. L., Liquid Velocity and Gas Hold Up in Three Phase Internal Loop Airlift Reactors with Low Density, Chemical Engineering Science, Vol. 50, No 8, pp. 1301-1310. 1995.         [ Links ]

[11] Cheng, Y. L. y Hwang, S. J., Gas Hold Up and Liquid Velocity in Three Phase Internal Loop Airlift reactors, Chemical Engineering Science, Vol. 52, No 8, pp. 3949-3860. 1997.         [ Links ]

[12] García, E. y Tobajas M., Hydrodynamics and Mass Transfer Prediction in a Three-Phase Airlift Reactor for Marine Sediment Biotreatment, Chemical, Engineering Science, vol. 54, p 5347-5354. 1999.         [ Links ]

[13] Molina G. E, García C, Sánchez, J., Mathematical Model of Microalgal Growth in Light Limited Chemostat Cultures, Journal chemical Technology and Biotechnology, pp. 167-173. 1994.         [ Links ]

[14] Ever, E. G., A model for Light-limited continuous cultures: Growth, shading, and maintenance, Biotechnology and Bioengineering, Vol. 38, pp. 254-259. 1990.         [ Links ]

[15] Eilers P.H. Y Petters J.C., A model for the relationship between light intensity and the rate of photosynthesis in phytoplankton, Ecological modeling, Vol. 42, pp. 199-215. 1988.         [ Links ]

[16] Wu X. y Merchuck J.C. A model integrating fluid dynamics in photosynthesis and photoinhibition processes, Chemical Engineering Science. Vol. 56, pp. 3527-3538. 2001.         [ Links ]