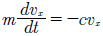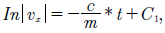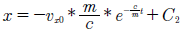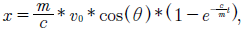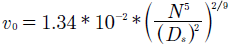1. INTRODUCCIÓN

En escenas del crimen, donde se ha cometido un delito en contra de un individuo, suelen encontrarse patrones de manchas de sangre, las cuales se convierten en un elemento de vital importancia en los procesos de reconstrucción de dichos hechos; de tal manera, que son una herramienta determinista para los peritos en criminalística. Como lo afirman Verdú et al.¹⁾⁽², los patrones de manchas de sangre permiten aproximar la forma en que se desarrolló un determinado suceso.

Los patrones de las manchas de sangre son los diagramas formados por las gotas que salen del cuerpo humano al momento de generar una herida con arma punzante, cortante, corto punzante, contundente o de fuego^3)(4)(5. Para analizar los patrones dejados en diferentes superficies, es necesario tener en cuenta factores que pueden incidir en la trayectoria de la gota, que se evidencian en la escena, como son: las dimensiones del patrón de mancha de sangre y el número de espinas, los cuales se pueden analizar a través de fundamentos físicos y matemáticos que ayudan a calcular la posible ubicación tanto de la víctima como del perpetuador del delito. Pese a la existencia de investigaciones previas a nivel internacional, a la fecha, no se conocen referencias que evidencien análisis exhaustivos de patrón de manchas. De acuerdo con lo anterior, a continuación, se describen conceptos claves para el desarrollo de esta propuesta.

La sangre es el único tejido del cuerpo humano que se encuentra en estado líquido. Contiene todos los elementos necesarios para el sustento de las células y todo el organismo del individuo. Está constituida en un 45% por células, como: eritrocitos que se encargan de transportar el oxígeno y proveer su color rojo característico; leucocitos encargados de la defensa e inmunidad y las plaquetas las cuales se encargan de la coagulación de la sangre⁶.

El restante 55% se denomina plasma y es el líquido en el que están contenidas las células sanguíneas, este, a su vez, está conformado por agua, encargada de transportar sustancias y absorber el calor; electrolitos tales como: el sodio, potasio, calcio, magnesio cloruro y bicarbonato, entre otros; y proteínas plasmáticas como albumina, fibrinógeno y globulina. El plasma también transporta otras sustancias: hormonas, glucosa, desechos y gases de respiración⁶. Para autores como⁷, los porcentajes entre el plasma y la parte celular de la sangre pueden cubrir un intervalo entre 54 - 55% y 44 - 45%, respectivamente.

La hematología forense se encarga de la identificación y caracterización de las manchas de sangre en la escena de un crimen⁸. Las manchas de sangre tienen diferentes características morfológicas, dependiendo de una diversidad de factores. Las formas y figuras pueden variar en tamaño y características dependiendo de la cantidad, calidad, origen, dimensión y profundidad de la lesión y características de la superficie donde se impregna³.

En su camino hacia la superficie, la gota de sangre puede seguir dos diferentes recorridos. El primero de ellos es una caída completamente vertical, el cual generará una mancha de forma esférica y una caída en movimiento parabólico, el cual generará una mancha ovalada de acuerdo con el ángulo de la trayectoria en su contacto con la superficie⁹.

Las manchas de sangre en una superficie pueden ser generadas a través de diferentes mecanismos: el primero, son las manchas por proyección, que consisten en gotas que viajan libremente por el espacio; otro mecanismo, son las manchas por contacto, las cuales se producen por el contacto con una superficie, con un elemento untado con sangre, por ejemplo, impresiones de manos, pies, rodillas u otras zonas corporales.

Otra opción, son las manchas por escurrimiento que generan regueros o charcos y se caracterizan por tener un gran volumen. Además, pueden ser las manchas por impregnación, que se presentan cuando se impregna con sangre una fibra, como tela o espuma. También pueden presentarse manchas por limpieza, las cuales pueden hallase en el piso con forma irregular y se identifican porque se evidencia un intento de borrarlas. Finalmente, se pueden presentar manchas de sangre por arrastre, las cuales se producen cuando la víctima se arrastra o es arrastrada.

De acuerdo con lo anterior, el objetivo de este trabajo es establecer ecuaciones que permitan determinar la trayectoria de una gota de sangre, incluyendo parámetros como la tensión superficial y la interacción de la gota con el aire, lo que permitirá una identificación más precisa del punto de origen de una gota de sangre a partir de su análisis en una escena del crimen. Dichas ecuaciones permitirán tener un método de análisis estructurado con base en procedimientos científicos irrefutables, que serán una herramienta fundamental para el establecimiento de la verdad y la impartición de justicia.

2. METODOLOGÍA

La investigación cuantitativa con nivel de profundidad exploratorio, descriptivo y correlacional; los cuales se describen a continuación. Inicialmente, se llevó a cabo una investigación con un enfoque exploratorio en el que se realizó una revisión bibliográfica del estado del arte de la temática de estudio. Luego, se utilizó un enfoque descriptivo, el cual permitió identificar las variables que se deben incluir en las ecuaciones utilizadas para analizar patrones de manchas. Finalmente, en un enfoque correlacional donde se identificó la relación entre las variables que permiten calcular la posición de los implicados en el hecho, a través del análisis del patrón de manchas.

El caso de estudio incluirá únicamente patrones de manchas de sangre impregnados en una superficie dura, lisa, no porosa y sin irregularidades, ya que la superficie representa un elemento diferenciador sobre la manera como se extiende el patrón de mancha.

3. RESULTADOS

Para determinar el punto de origen de una gota de sangre a partir de la impresión hemática encontrada en la escena del crimen, es necesario calcular de la manera más precisa posible la trayectoria que esta siguió. Debido a la acción de la fuerza de la gravedad y en ausencia de cualquier otra fuerza, todos los objetos dentro de la atmósfera de la tierra son atraídos hacia su centro, de esta manera, se puede afirmar que todos los objetos bajo estas condiciones irremediablemente caerán. La trayectoria que siguen los objetos durante su caída dependerá de su velocidad en el momento de ser liberados por la acción de la fuerza de la gravedad. Si el objeto se encontraba en reposo o su velocidad inicial estaba alineada con el sentido de la fuerza gravitacional, el objeto seguirá una línea recta vertical. Por el contrario, en el caso más general, donde la velocidad inicial del objeto está orientada de manera diagonal, la trayectoria de la gota será una parábola invertida, lo cual se conoce como movimiento parabólico.

En el caso ideal, el cual facilita los cálculos, una gota de sangre se desplaza únicamente por la acción de la fuerza de la gravedad, por lo cual seguirá una trayectoria dada por el movimiento parabólico. Este es un movimiento bidimensional que se compone de una parte horizontal, donde no actúa ninguna fuerza, y una parte vertical en la que actúa la fuerza de la gravedad produciendo una aceleración conocida como.

Es bien conocido que en el eje horizontal x el movimiento tiene una velocidad constante, de tal manera que su desplazamiento, iniciando en el origen de un sistema cartesiano, puede describirse como:

donde υ ₀ es la magnitud de la velocidad inicial del movimiento, υ es el ángulo de lanzamiento, medido respecto a la horizontal ytes el tiempo. En cualquier punto de la trayectoria, la velocidad horizontal de la partícula será:

el cual es un valor constante que corresponde a la componente horizontal de la velocidad inicial de la gota de sangre, υ _x0 .

Para encontrar la altura de la gota en cualquier instante de tiempo, considerando que el desplazamiento inicia en el origen del sistema de coordenadas, se usa la expresión

donde la velocidad inicial vertical de la partícula es υ _y0 = υ ₀ *sen(θ). En este caso, la velocidad vertical de la gota está dada por

Las ecuaciones (1) a (4) son muy usadas para el describir el movimiento parabólico, solo consideran uno de los fenómenos involucrados en el movimiento.

Con el fin de mejorar la aproximación, se considerará la interacción con el aire de la gota de sangre en su trayectoria. Para esto se hará uso de las leyes de movimiento de Newton. En este caso, el aire se comporta como un fluido que ejerce resistencia al desplazamiento de la gota de sangre en su movimiento, que se presenta como una fuerza resistiva que puede ser modelada como directamente proporcional a la velocidad instantánea de la gota.

Ubicando el origen de un sistema de coordenadas cartesiano, en el punto inicial del movimiento, como en la sección anterior, se usará el ejexpara describir el movimiento horizontal y el ejeypara el movimiento vertical. Según la segunda ley de Newton, el sistema puede ser descrito vectorialmente por:

Donde = (υ _x , υ _z ) es la velocidad de la gota de sangre,  = (0, - g) es la aceleración debida a la fuerza de la gravedad yces una constante positiva que caracteriza la resistencia del aire. Como en el caso del movimiento parabólico, la ecuación (5) puede ser escrita de forma independiente para cada uno de sus componentes, de tal manera que para el ejexresulta en:

y para el ejeyen:

La ecuación (6) corresponde a una ecuación diferencial de segundo orden que puede ser resuelta por el criterio de ecuación diferencial exacta. Despejando adecuadamente y aplicando el operador integración se tiene:

Solucionando a ambos lados resulta:

dondeC ₁  es la constante de integración. Es posible encontrarC ₁  considerando que, para el tiempo inicialt = 0la velocidad de la gota de sangre corresponde a su velocidad inicial en el ejex, es decir, υ = υ _x0 . Despejando la velocidad en el ejexse obtiene:

Generalmente, el movimiento parabólico considera que la componente de la velocidad en el ejexse mantiene constante; sin embargo, a partir de la ecuación (10) puede notarse que, cuando se considera la interacción de la gota de sangre con el aire, la componente de la velocidad enxdisminuye de manera exponencial con el tiempo.

A partir de la función de la velocidad en el ejex, es posible conocer la función de la posición. Entendiendo a la velocidad como la primera derivada de la posición, se integra, y aplicando de nuevo el criterio de ecuación diferencial exacta se tiene:

En este caso, la condición de contorno implica que, en el tiempo inicial, la gota de sangre se encontraba en el origen del sistema de coordenadas, calculandoC ₂  y agrupando términos, se tiene:

Las ecuaciones (10) y (12) determinan la posición y velocidad de la gota de sangre, en el ejex, en cualquier instante de tiempo cuando se considera la interacción con el aire.

Es importante notar que, en el caso particular de un medio poco resistivo en el que se desplaza un objeto masivo se cumplirá la aproximaciónc << m. Aplicando la afirmación anterior para la aproximación mediante series de McLaurin¹⁰sobre las ecuaciones (10) y (12) se encontrarán las ecuaciones (1) y (2), respectivamente.

La ecuación (7) también corresponde a una ecuación diferencial de segundo orden, de tal manera que para encontrar las funciones de posición y velocidad en el eje y se seguirá un análisis semejante al utilizado anteriormente para el ejex. Despejando y aplicando la función integración se obtiene:

Solucionando la integral a ambos lados se tiene:

Mediante la condición de contorno que indica que, en el tiempo inicial, la velocidad de la gota de sangre en el ejeycorresponde la velocidad vertical inicial de la partícula, υ = υ _y0 ., de esta manera es posible hallarC ₃  y la función para la velocidad vertical resulta en:

A partir de la ecuación (15) es posible calcular la función de la posición en el eje vertical y usando la función velocidad en el mismo eje. Para esto, se aplica una operación semejante a la presentada en la ecuación (11), la cual se soluciona para obtener:

La posición y velocidad de la gota de sangre en el eje y para cualquier tiempotestán caracterizadas por las ecuaciones (15) y (16), respectivamente. De nuevo, las ecuaciones (3) y (4) que caracterizan posición y velocidad cuando se desprecia la interacción con el aire, pueden encontrarse a partir de (15) y (16), utilizando la aproximación en series de McLaurin con la condiciónc << m.

Como se mencionó anteriormente, en el caso más general, la velocidad inicial de una gota de sangre seguirá una línea diagonal que puede descomponerse en los ejesxey; debido a esto, es de esperarse que, en el momento del impacto, exista un ángulo relativo entre el vector de la velocidad de la gota de sangre y la línea perpendicular a la superficie¹¹. Lo anterior puede notarse cuando se encuentran gotas de sangre en la escena de un crimen, ya que las manchas encontradas suelen tener una forma elíptica. La Fig. 1 presenta, a modo de ejemplo, un esquema que puede ser utilizado para determinar el ángulo de impacto υ, donde se exageran los tamaños, por el fin ilustrativo.

Debido a lo anterior, para determinar el ángulo υ de una gota de sangre, es posible usar una relación trigonométrica considerando únicamente el diámetro menor de la mancha,dsy el diámetro mayor,Ds, tal que:

Si los diámetrosdsyDsson iguales la mancha generada por la gota tiene forma circular, lo que corresponde con un ángulo de impacto υ = 0, para encontrar el ángulo de lanzamiento, υ, respecto del ángulo de impacto, υ, se usa la relación:

Cuando una gota de sangre golpea una superficie, esta se deforma, de tal manera que sus componentes tienden a separarse. Dependiendo de las condiciones del impacto, la gota deja una impresión hemática de dimensiones específicas, en donde el diámetroD _o  está relacionado con la velocidad de impacto y la densidad del líquido. Después de la colisión, también sucede que parte de la gota de sangre sale disparada formando lo que se conoce como espinas alrededor de la periferia de la mancha.

El tamaño de las manchas de sangre y el número de espinas dependerán entonces de la velocidad de impacto de la gota y del diámetro de la gota. Es posible, por lo tanto, deducir el tamaño y la velocidad de la gota midiendo el diámetro de la mancha y contando el número de espinas.

La dispersión de la gota está restringida por la viscosidad (υ) y la tensión superficial (υ). Una gota alcanza su máxima caída cuando estas fuerzas opuestas se equilibran entre sí. La relación entre la inercia del fluido y las fuerzas viscosas se expresa por una razón adimensional, definida como el número de Reynolds,Re, y está dada por:

la relación entre la inercia y las fuerzas de tensión superficial se expresan por el número de Weber,We:

En¹²desarrollaron un modelo para predecir el diámetro máximo de propagación de la gota,D _max , después del impacto. Mostraron que cuando la inercia de la gota que impacta es suficientemente alta, las fuerzas de tensión superficial son insignificantes y el diámetro de la gota máximo es función solo del número de Reynolds. Este modelo se probó en una amplia gama de números de Reynolds y Weber y se encontró que se correlaciona bien con los datos experimentales. Ellos demostraron que los efectos de la tensión superficial son insignificantes siWe >> Re ^1/2 , una condición satisfecha en los experimentos realizados, en cuyo caso el factor de dispersión máximo(D _max /D ₀ )fue:

La ecuación anterior prediceD _max  que corresponde a la extensión máxima de la dispersión de la gota, no el diámetro final de la manchaD _s . Sin embargo, dado que hay poco retroceso de la gota, se asume queD _max  es aproximadamente igual aD _s .

En¹³se sugirió que las espinas se forman a lo largo de los bordes de las gotas dispersas debido a la inestabilidad de Rayleigh-Taylor, que surge cuando la interfaz entre un líquido y el gas se desacelera rápidamente, como sucede a lo largo del borde de una gota dispersa. La inestabilidad crea ondulaciones en la superficie del líquido que crecen y forman la espina.

En¹⁴fotografiaron impactos de gotas de agua y mostraron que el número de espinas permaneció constante durante la propagación de la gota. Mientras que en¹⁵realizaron un análisis detallado de la inestabilidad y resolvieron numéricamente las ecuaciones gobernantes para calcular el número de espinas (N) que pueden crearse para un conjunto dado de condiciones de impacto. También en¹⁶⁾⁽¹⁷encontraron una solución analítica para las ecuaciones y mostraron que el número de espinas se puede predecir con una precisión razonable de la siguiente manera:

Existen diferencias entre las predicciones de las dos ecuaciones descritas anteriormente (21), (22) y las mediciones experimentales, debido a las incertidumbres en las mediciones de las propiedades y de la rugosidad del material. Para mejorar la concordancia entre los valores calculados y medidos, se introducen dos factores de corrección empíricos,C _d  yC _n , de manera que:

La selección deC _n = 0:838yC _d = 1:11dio los mejores ajustes de las ecuaciones (23) y (24) comparado con los datos experimentales.

Usando estos valores se obtuvieron expresiones explícitas para la velocidad de impacto (υ ₀ ) y el diámetro inicial de la gota (D ₀ ) en términos del número de espinas y el diámetro de la mancha al combinar las ecuaciones (25) y (26) con las definiciones deReyWepresentadas en las ecuaciones (19) y (20). Después de operaciones algebraicas, se obtiene:

Finalmente, sustituyendo ρ = 1062 kg/m ³ , μ =0.0048 kg/m.sy σ = 0.056 N/m, se obtiene:

En los cálculos anteriores no se tuvieron en cuenta las posibles variaciones debidas a la superficie. Una superficie rugosa puede generar variaciones en el diámetro medido de la mancha.

4. DISCUSIÓN Y CONCLUSIONES

Teniendo en cuenta lo antes descrito, el investigador forense debe medirDsyNdespués de documentar y fotografiar correctamente la mancha de sangre. De vuelta en el laboratorio, gotas de sangre del tamaño conocido deben dejarse caer en una superficie idéntica desde diferentes alturas para formar manchas. Siempre que sea posible, el uso de una muestra de la superficie de la escena del crimen en cuestión dará la mayor precisión.

De acuerdo con el análisis realizado para obtener las ecuaciones (27) y (28), se recomienda que para mejorar la precisión y proporcionar un mayor valor de evidencia, se deben realizar pruebas para cada superficie en particular, en la que se observan manchas de sangre.

Las ecuaciones (27) y (28) serán de utilidad para calcular los diámetros iniciales de las gotas y las velocidades de impacto a partir de las mediciones del diámetro de las manchas de sangre y el número de espinas. De esta manera, reemplazando las ecuaciones (18), (17) y (27) en (12) y (16) es posible estimar con una buena aproximación las posiciones vertical y horizontal del punto de origen de la gota de sangre.