1. INTRODUCCIÓN
A partir de la década de 1920 la estabilidad de los sistemas eléctricos de potencia (SEP) fue reconocida como un importante problema para su funcionamiento seguro. La estabilidad tiene muchas aristas de análisis, siendo la estabilidad de voltaje una de las más relevantes [1]. El crecimiento continuo de los sistemas eléctricos de potencia, con cambios en sus variables eléctricas y la evolución de nuevas tecnologías ha provocado una nueva forma de encarar el estudio y análisis de la estabilidad [2]. Las oscilaciones inter-área, la estabilidad de voltaje y frecuencia han ganado prioridad sobre otras formas de inestabilidades. Los sistemas eléctricos de potencia sufren en forma continua una gran variedad de perturbaciones graves o leves, las cuales pueden aparecer en forma de pequeñas perturbaciones [3] (cambios de carga) o más graves como un cortocircuito en una línea o salida de un generador de gran potencia a lo cual el sistema debe poder adaptarse y funcionar favorablemente. Cuando se produce una perturbación hay dos posibles estados posteriores resultantes; que el sistema conserve su estabilidad, o que el sistema entre en un proceso de inestabilidad que provoque un efecto dominó tras la desconexión de algunos elementos y, finalmente, un posible colapso de voltaje o pérdida de sincronismo en generadores [4].
La estabilidad en los SEP tiene que ver con el comportamiento dinámico y en estado estable del sistema. La determinación de los límites de transferencia de energía eléctrica es una tarea fundamental para garantizar la seguridad de los sistemas de energía eléctrica [5], donde dichos sistemas son altamente no lineales y están expuestos a variaciones de carga en forma constante. En las líneas de transmisión desde el punto de vista eléctrico, la máxima transferencia de energía por los conductores se obtiene mediante la estimación de límites operativos entre los cuales se considera, límite térmico, límite por caída de voltaje y límite por margen de estabilidad [6]. Situación similar ocurre en transformadores de potencia, en los cuales fallas de tipo eléctrico, térmico y mecánico pueden darse, se considera que el 61% de las fallas están asociadas con condiciones externas; es decir, con el sistema al cual está conectado, un 7% por sobre corrientes, un 4% por fallas en barras colectoras y un 13% por factores no detectados [7]. En generadores sincrónicos, además de límites de tipo térmicos, existen limitaciones mecánicas de las turbinas y restricciones operativas impuestas por el sistema de potencia. Las restricciones de los componentes eléctricos consideran los límites de calentamiento de los bobinados del estator y rotor, en tanto que las restricciones de tipo mecánico están impuestas por el equipo que transforma la fuente primaria de energía en energía mecánica. Cuando un generador sincrónico funciona en condición de sub excitación se deben definir criterios de márgenes de estabilidad, lo cual permitirá entregar con bajas corrientes de campo la potencia necesaria al sistema [8].
Un sistema es estable cuando al presentarse contingencias de origen eléctrico o mecánico el sistema recobra sus condiciones de equilibrio [2]. Este equilibrio en régimen permanente, solo puede lograrse con un estudio cuidadoso del comportamiento de sus componentes y estudiando sus curvas de capacidad, características que definen los límites operativos de los equipos involucrados, entendiendo estos límites como el máximo flujo de potencia posible que puede circular por un punto particular del sistema de potencia [9]. El mantenimiento de la estabilidad en un sistema es de vital importancia debido a que una deficiencia en este comportamiento hace al sistema inoperable [10], representando incluso pérdidas económicas por energía no suministrada en los puntos de carga. Aspectos como la impedancia de los sistemas de transmisión y transformadores juegan un papel importante en la estabilidad de un sistema. Las características de regulación en las máquinas sincrónicas también lo son. Los estudios de estabilidad de los sistemas de potencia inevitablemente están relacionados, por ejemplo, con estudios de estabilidad de voltaje. Dentro de los métodos clásicos de análisis están: simulación en el dominio del tiempo, análisis de sensibilidad a través de matrices jacobianas, análisis nodales de valores propios, estimación de los valores máximos de operación mediante curvas PV y QV, por nombrar algunos. En años recientes se ha optado por el uso de índices de estabilidad de voltaje con la implementación de PMU (Phasor Measurement Unit), los cuáles proveen información en tiempo real que permiten supervisar el estado del sistema continuamente. Las aplicaciones de redes de comunicaciones, tales como las redes WAMS [11]. (sistema de monitoreo de área extendida) juntamente con las PMU y un sistema de enlace satelital de posicionamiento global (GPS) ha hecho posible tener un control sobre la estabilidad de un SEP mediante la identificación oportuna de modos de oscilación. Lo anterior permite operar el sistema en tiempo real a partir de datos dinámicos [12].
En este trabajo se desarrolla un método para supervisar el estado de los equipos principales de un SEP como son generadores, transformadores y líneas de transmisión cuando estos trabajan en el límite de su capacidad de funcionamiento de tal manera de pronosticar a partir de los datos obtenidos, la continuidad de la estabilidad en estado estable o permanente. Se han desarrollado las ecuaciones que permiten hacer los gráficos de las curvas de los límites operativos de cada equipo involucrado y a partir de esto se ha definido los algoritmos pertinentes que ingresados en el entorno Matlab dibujará las gráficas que se utilizarán para dicha investigación. Se ha seleccionado como caso de estudio el sistema de 39 barras de la IEEE [13]. Para reproducir los diferentes escenarios en los que se analizará el problema propuesto. Para esto se utiliza el programa PowerFactory en el cuál a partir de datos obtenidos de flujos de potencia son enviados vía programación realizada en DPL al programa Matlab. El programa permite simular condiciones de contingencias en las cuáles la pérdida de un generador, un transformador o una línea de transmisión se hayan producido.
2. LÍMITES DE OPERACIÓN
Los generadores, líneas de transmisión y transformadores tienen límites operativos que deben ser observados para verificar la estabilidad permanente de un sistema de potencia. La estabilidad permanente se verifica si el punto de operación de un elemento se encuentra dentro de los límites de operación a pesar de haber existido una contingencia, cuya etapa transitoria ha sido superada exitosamente [14].
2.1 Transformadores
La duración de la vida de un transformador se encuentra muy vinculada con la cargabilidad de sí mismo, partiendo de que la vida útil de un transformador se puede asimilar a la vida de su aislamiento sólido [15]. Un transformador que funciona en regímenes de carga muy elevados con temperaturas de operación superiores a los 140 °C [16] ve reducida la vida de su aislamiento a un ritmo mucho más alto que un transformador que trabaja en regímenes de carga inferiores. Estimar el estado constante de los transformadores de potencia debido al deterioro de sus aislamientos es un elemento decisivo para prevenir riesgos asociados a la estabilidad y confiabilidad de las líneas de transmisión y claro también para mantener un servicio eléctrico de calidad [17].
La curva de capacidad de los transformadores se modela como un círculo de radio igual a la potencia aparente nominal del transformador; y sus ejes coordenados representan en x la potencia activa y en y la potencia reactiva, respectivamente. La curva resultante se indica en la Fig. 1. El lugar geométrico que describe la potencia aparente en el plano PQ viene dado por la siguiente expresión:
2.2 Generador sincrónico
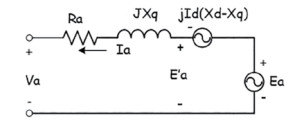
El generador sincrónico es una parte importante dentro de un sistema de potencia, pues proporciona la potencia eléctrica que es requerida por las cargas. Estas máquinas rotativas tienen sus límites definidos por las curvas de potencia reactiva del generador proporcionada por los fabricantes. Estas curvas se trazan al representar los limitantes que tienen los generadores durante su operación [18] . La forma de modelar la curva de capacidad de los generadores sincrónicos se basa en el diagrama fasorial [19] del circuito equivalente (Figs. 2 y 3). Para generalizar el modelo lo más adecuado es tomar al generador sincrónico con rotor tipo polos salientes. Los generadores de polos salientes utilizan la teoría de los dos ejes para explicar el comportamiento de la máquina sincrónica en modo generador. Utilizando esta teoría se puede modelar en forma gráfica los límites de operación del generador [20].
La curva de capacidad de un generador de polos salientes se indica en la Fig. 4, en la que su zona de funcionamiento seguro viene delimitada por los límites de operación tanto de índole mecánico como eléctrico [22] [23] .
Los factores intervienen en las ecuaciones que permiten trazar la curva de generador sincrónico y el modelo que describe los lugares geométricos de cada límite se indica a continuación:
Potencia mecánica: valores impuestos por la turbina que mueve el rotor del generador. El límite mínimo depende del tipo de central de generador, un valor aceptable puede ser 15%.
Corriente de campo: se define como las corrientes máxima y mínima que puede circular por el devanado del rotor. En el caso de la máxima corriente se relaciona con la corriente nominal del mencionado devanado. Al respecto de la mínima corriente tiene que ver con la operación en modo de consumo de potencia reactiva del generador [24] . Las ecuaciones que modelan el lugar geométrico de estos dos límites se indican a continuación:
Margen de estabilidad en estado estable: este límite se refiere a la potencia reactiva mínima que puede absorber un generador sincrónico, un margen de estabilidad típico puede ir entre el 15% a 25% [25].
2.3 Líneas de transmisión
La vida útil de una línea de transmisión depende de los niveles máximos permisibles bajo los cuales opera. La cargabilidad de una línea puede valorarse a partir de la relación de flujo de potencia activa contra potencia reactiva (P-Q) a través de sí misma o de una curva de la longitud de la línea en función de la potencia activa referida al SIL de la línea (Surge Impedance Loading) [26].
Esta última curva representa los límites de operación de las líneas de transmisión que son conocidas como curvas Saint Clair [13]. La cargabilidad de una línea de transmisión indica la capacidad de potencia que puede fluir por la línea bajo condiciones de operación aceptables; y está en función del calibre y de la longitud de la línea [27]. Los límites de capacidad en las curvas de Saint Clair son:
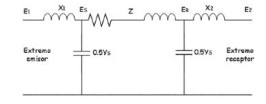
El modelo de línea empleado para formar la curva de capacidad se indica en la Fig. 6, la cual emplea el modelo pi de una línea de transmisión con parámetros concentrados [28].
La modelación de estas curvas se basa en definir los lugares geométricos de las potencias de envío y recepción en los extremos de una línea.
Potencia en el terminal de envío:
Potencia en el terminal de recepción:
Impedancia característica:
La potencia activa en la recepción en función del SIL:
3. METODOLOGÍA PROPUESTA
Por medio de la utilización de los paquetes computacionales PowerFactory y Matlab se logra estimar el comportamiento en régimen permanente de generadores, transformadores y líneas de transmisión, a partir de ubicar en las curvas de capacidad de cada elemento la condición operativa, en la cual se encuentran estos componentes, luego que el sistema haya superado una contingencia y se encuentre nuevamente en régimen permanente. Si el elemento opera dentro de sus límites, en el tiempo será estable, caso contrario su punto operativo podrá ser considerado como inestable.
Para este propósito, mediante instrucciones del lenguaje utilizado en PowerFactory, es posible interactuar con Matlab, enviando todo tipo de información, tal como parámetros de generadores, transformadores y líneas, además de resultados de condiciones operativas poscontingencias. Matlab procesa esa información por medio de los modelos descritos anteriormente para realizar los gráficos de los puntos de operación y definir si el sistema es estable en régimen permanente.
3.1 Sistema de prueba
Para probar la herramienta desarrollada se utiliza el sistema IEEE de 39 barras denominado en la literatura New England [13] . Este sistema de potencia tiene todas las características para servir como banco de ensayos; y así ha sido utilizado a lo largo de los años. De este sistema se obtienen las respuestas de los generadores, transformadores y líneas que el usuario desee conocer a partir de una contingencia. En la Fig. 7 se presenta el diagrama unifilar de la red de prueba seleccionada.
4. RESULTADOS
Se han escogido para el análisis algunos generadores, transformadores y líneas de transmisión, los cuáles de han desconectado, asumiendo que han sufrido algún tipo de contingencia, obligándose a salir súbitamente de operación. En las curvas de capacidad de cada elemento se evidencia su condición de funcionamiento, el punto visible en la gráfica (par ordenado) se ubica dentro de su zona de funcionamiento normal o fuera de ella indicando una sobrecarga en los equipos seleccionados. De esta manera, el modelo desarrollado puede ser escalable a cualquier sistema de potencia y cualquier contingencia n-1, n-2 o la desconexión de los equipos que se elija visualizando la condición de funcionamiento del resto de equipos dentro del modelo elegido.
En la Tabla I se presentan las contingencias propuestas para probar la herramienta desarrollada. Para cada caso se indican los resultados relevantes en cuanto a punto de operación de ciertos elementos del SEP, los que operan o no dentro de la curva de capacidad. Se escogen algunas contingencias, ya que estas tienen un carácter combinatorio, es decir, mientras mayor tamaño tenga el SEP, el número de posibles contingencias crece exponencialmente.
La herramienta desarrollada es de característica gráfica y pretende darle al operador del SEP un instrumento de decisión sobre qué generador, transformador o línea de transmisión no está operando dentro de sus limites luego de ocurrir una contingencia, dando paso a las acciones remediales que consten en los procedimientos de operación del sistema.
La Fig. 8 presenta los resultados de varios elementos dados por la herramienta desarrollada con los softwares PowerFactory y Matlab para contingencias simples. Esto permite notar de forma visual los posibles problemas en elementos del sistema y servir como alarma para los operadores. Asimismo, la Fig. 9 presenta resultados para las contingencias dobles y la Fig. 10 para la contingencia múltiple propuesta.
Los resultados gráficos deducir que las consecuencias producidas en un SEP son fundamentalmente función del tipo de contingencia y equipo en el cual se produjo tal evento. Así, por ejemplo, se puede observar que en las curvas obtenidas hay más repercusión cuando un generador o transformador sale de la red que cuando sale una línea de transmisión (contingencia n-1).
Mientras más equipos salgan simultáneamente el sistema estará más cerca de un colapso como lo prueba al producir una falla en dos líneas de transmisión en forma simultánea (contingencia n-2). Además, las contingencias múltiples en su mayoría pueden conducir a un colapso porque varios elementos quedan trabajando fuera de sus zonas seguras de operación. La herramienta de supervisión presentada puede evitar un colapso al exponer aquellos elementos que se encuentren más perjudicados en su funcionamiento, ya que sobre estos se debe actuar de forma inmediata. En la Tabla II consta la valoración de un tipo de contingencia sobre el sistema, situación que se ha podido comprobar con la herramienta expuesta en este trabajo.
5. CONCLUSIONES
La supervisión de los sistemas de potencia es una acción preventiva que puede evitar colapsos mayores que traen consigo la pérdida del servicio en los usuarios. Las nuevas tecnologías de medición en tiempo real donde se emplean PMU pueden ser una alternativa viable para alimentar la información de la herramienta desarrollada al transformarse en un análisis en línea.
Los modelos matemáticos que permiten evaluar si un elemento del SEP opera dentro de sus límites son los lugares geométricos que describen los valores máximos de potencia que puede atravesar una línea, un transformador o un generador.
La herramienta desarrollada permite realizar un análisis fuera de línea que puede ser empleado para establecer estrategias de operación que impidan que los elementos del SEP ante contingencias con una alta probabilidad de ocurrencia permanezcan en zonas inseguras de operación y que al poco tiempo resulten en una desconexión.