Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellín vol.8 no.15 suppl.1 Medellín July 2009
La calculadora analógica de Lagrange para las integrales elípticas
Lagrange's analog calculator for elliptic integrals
Leonardo Solanilla Ch*; Ana Celi Tamayo A**; Gabriel A Pareja O***
* Ph. D. en Matemáticas, Tulane University. Profesor de planta, Departamento de Matemáticas y Estadística, Facultad de Ciencias, Universidad del Tolima, Barrio Santa Elena, Ibagué, Colombia. Telefax: (098)2669162. Email: leonsolc@ut.edu.co
** M. Sc. en Educación con énfasis en la Enseñanza de las Matemáticas, Universidad de Antioquia. Profesora de planta, Departamento de Ciencias Básicas, Universidad de Medellín, Medellín, Colombia. Telefax: (094)3405442. Email: actamayo@udem.edu.co
*** Matemático, Universidad de Antioquia. Profesor catedrático, Departamento de Ciencias Básicas, Universidad de Medellín, Medellín, Colombia.Telefax: (094)3405442. Email: gpareja@ayura.udea.edu.co
Resumen
En este artículo se muestra que el modelo esférico de Lagrange para las integrales elípticas es interpretable como un computador analógico. Además del lema fundamental que sustenta la analogía, se presentan ejemplos de cálculo para las amplitudes de la suma y la diferencia de dos amplitudes elípticas dadas. En el computador analógico, estas operaciones se materializan por medio de construcciones con regla y compás esféricos. A lo largo de la presentación, se discuten las ventajas y desventajas del procedimiento propuesto. Al final, se esbozan algunas conclusiones sobre los métodos usados y sobre un posible método híbrido para la aproximación numérica de las amplitudes elípticas.
Palabras clave: funciones e integrales elípticas, trigonometría esférica, computadoras analógicas, construcciones geométricas.Abstract
In this paper, we show that Lagrange's spherical model for elliptic integrals can be understood as an actual analog computer. In addition to proving the fundamental lemma establishing analogy, we provide examples which show a way to compute the amplitude of the addition (and subtraction) of two elliptic integrals. In our computer, these operations are performed by using a spherical compass and a spherical straightedge. We also discuss the pros and cons of our procedure. At the end, we draw some conclusions concerning the possibility of alternative hybrid numerical solutions to the elliptic amplitudes.
Key words: elliptic functions, elliptic integrals, spherical trigonometry, analog computers, geometric constructions.
INTRODUCCIÓN
La circunferencia y la esfera no sólo son figuras geométricas que ayudan a modelar el mundo, sino también poderosas formas del pensamiento que inspiran la construcción de máquinas de cálculo. Además del astrolabio y la esfera armilar, baste con mencionar el antiquísimo mecanismo de Anticitera [1] y el integrador mecánico soñado por Coriolis [2], ancestro común del analizador diferencial y del intégrafo.
Cuando dos realidades matemáticas o físicas se describen por una misma ecuación diferencial, una de ellas puede usarse para inferir comportamientos o predecir sobre la otra. Este es el principio de los computadores analógicos. El auge de la electrónica ha hecho que hoy predominen las calculadoras analógicas eléctricas [3]; aunque también existen mecánicas e hidráulicas. En este artículo se describe un modelo mecánico que utiliza una esfera para calcular la amplitud de la adición de ciertas integrales elípticas.
Las integrales elípticas surgen naturalmente en problemas de Física e Ingeniería. Entre otros muchos contextos, ellas aparecen en el estudio del péndulo simple no linealizado, la flexión de una barra delgada [4] o el campo magnético generado por n bobinas alineadas axialmente [5]. De por sí, ellas constituyen una clase completa de integrales conocidas desde los albores del cálculo infinitesimal [6] que vieron su cenit a finales del siglo XVIII, justo antes de que el interés de los matemáticos se dirigiera hacia la moderna teoría de la funciones elípticas. Una integral elíptica (de la primera especie) puede reducirse siempre a la forma

donde  para 0 < k < 1 fijo. En general, estas integrales no se dejan tratar por los métodos usuales de integración y, así, no es posible evaluarlas por medio de funciones elementales. Por ello, se acostumbraba aproximarlas numéricamente para valores igualmente espaciados de Φ y presentarlas en forma de tablas. Hoy, el computador digital facilita grandemente el cómputo de dichos valores aproximados. En contraste, el procedimiento de cómputo que se describe más adelante es puramenteanalógico.
para 0 < k < 1 fijo. En general, estas integrales no se dejan tratar por los métodos usuales de integración y, así, no es posible evaluarlas por medio de funciones elementales. Por ello, se acostumbraba aproximarlas numéricamente para valores igualmente espaciados de Φ y presentarlas en forma de tablas. Hoy, el computador digital facilita grandemente el cómputo de dichos valores aproximados. En contraste, el procedimiento de cómputo que se describe más adelante es puramenteanalógico.
Las propiedades más importantes de estas integrales se desprenden de la solución al problema con valor inicial
En verdad, la fórmula de adición es válida si y sólo si se cumple la identidad de Lagrange
A menudo conviene escribir  y
y  . La inyectividad de F permite entonces escribir y. De esta forma, la fórmula de adición se reduce a
. La inyectividad de F permite entonces escribir y. De esta forma, la fórmula de adición se reduce a 
Ya que F se extiende naturalmente a una función impar en el intervalo  el cambio de signo
el cambio de signo  produce la fórmula de substracción
produce la fórmula de substracción  si y sólo si
si y sólo si  . Esta es la solución al problema
. Esta es la solución al problema 
 Los detalles matemáticos e históricos de la teoría de las integrales elípticas se pueden consultar en el completísimo texto de Bellachi [7].
Los detalles matemáticos e históricos de la teoría de las integrales elípticas se pueden consultar en el completísimo texto de Bellachi [7].
En la primera sección del artículo se prueba que la ecuación diferencial que satisface cierto tipo de deformación de un triángulo esférico coincide esencialmente con (1). De esta manera, el estudio de la dinámica de dichos triángulos esféricos provee un modelo para estudiar las integrales elípticas y sus fórmulas de adición. La segunda sección está dedicada a nuestra interpretación del procedimiento de Lagrange para calcular la amplitud de la suma y la resta de dos integrales elípticas. No conocemos ningún documento donde se relacione este procedimiento con las construcciones con regla y compás. Además, se presenta un ejemplo completo de cálculo con ayuda de los teoremas de la trigonometría esférica. La sección finaliza con una evaluación de las ventajas y desventajas del método analógico propuesto. La sección tres discute el asunto de la construcción de tablas para ángulos igualmente espaciados. Allí se hace necesario apelar a la teoría de los triángulos esféricos rectángulos. Al final, se esbozan algunas conclusiones sobre lo encontrado y sobre posibles sendas a seguir en el futuro.
1. ANALOGÍA ESFÉRICA
Lagrange [8] se percató que las identidades para cos ν y cos μ son casos de la ley de los cosenos de la trigonometría esférica, según el vértice opuesto sea agudo u obtuso. Este hecho lo llevó, probablemente, a buscar un modelo para las integrales elípticas en la esfera.
De ahora en adelante se asume que el lector está familiarizado con los elementos básicos de la trigonometría esférica; tal como se presentan, por ejemplo, en Ayres [9]. Sea, pues, ABC un triángulo esférico de lados a, b, c, con ángulos opuestos respectivos o vértices A, B, C. Cuando ABC se deforma suavemente, sus lados a, b, c son funciones diferenciables de cierta variable independiente t, a la que se interpreta como tiempo.
Definición 1.1. (Deformación lagrangiana). Se dice que ABC está sufriendo (instantáneamente) una deformación lagrangiana si las velocidades de C y c son nulas mientras que las velocidades de a y b yacen sobre las rectas tangentes a CB y CA en los puntos B y A, respectivamente, . (Figura 1).
Para todo lo que sigue, no sobra insistir en que k es un valor constante en el intervalo (0, 1).
Lema 1.2. Sea ABC un triángulo esférico. Las tres afirmaciones siguientes son equivalentes:
(i) ABC está sufriendo una deformación lagrangiana.
(ii) Las funciones a, b satisfacen una de las ecuaciones diferenciales

(iii) En la ley de los cosenos
 la ley de los senos
la ley de los senos  c permanece constante mientras a, b varían suavemente.
c permanece constante mientras a, b varían suavemente.
Demostración. La verificación de  consiste en una simple aplicación del método de integración de Lagrange [10]; por ello, no se incluye aquí. Para el resto de la prueba la figura 1 puede servir de ayuda. Supongamos que (i) se cumple. En el plano tangente a la esfera en A encontramos que la contribución de la derivada de b a la derivada de c es
consiste en una simple aplicación del método de integración de Lagrange [10]; por ello, no se incluye aquí. Para el resto de la prueba la figura 1 puede servir de ayuda. Supongamos que (i) se cumple. En el plano tangente a la esfera en A encontramos que la contribución de la derivada de b a la derivada de c es  De forma similar, la proyección de la derivada de a en la dirección de c en el punto B es
De forma similar, la proyección de la derivada de a en la dirección de c en el punto B es  Por hipótesis,
Por hipótesis,  o sea,
o sea,

Ahora bien, la trigonometría esférica enseña que  (respectivamente
(respectivamente  El signo distingue los casos en que A (respectivamente B ) es agudo u obtuso. Por tanto, se sigue (ii). El argumento se puede invertir, es decir, (ii)
El signo distingue los casos en que A (respectivamente B ) es agudo u obtuso. Por tanto, se sigue (ii). El argumento se puede invertir, es decir, (ii) 
Este lema muestra que la dinámica de la deformación lagrangiana de los triángulos esféricos cumple la misma ecuación diferencial o ley de las integrales elípticas. Este hecho permite la construcción de la calculadora analógica de Lagrange.
Hasta aquí, todo parece indicar que para construir una máquina que implemente esta dinámica, es preciso saber a cada instante cuándo a (respectivamente b) crece o decrece, y cuándo A (respectivamente B) es agudo, recto u obtuso. A propósito, no sobra recordar en este punto la condición global de Gauss–Bonnet A + B + C > π, v. e. g. [11]. Así pues, si alguno de estos tres ángulos es obtuso, tal condición queda satisfecha y los dos restantes pueden ser agudos, rectos u obtusos.
2. ADICIÓN Y SUBSTRACCIÓN
En verdad, no se precisa saber exactamente el signo de las cantidades mencionadas en el párrafo anterior. Esto es consecuencia de una ingeniosa construcción geométrica debida al mismo Lagrange [8]. Es interesante notar que tal construcción involucra solamente meridianos y circunferencias sobre la superficie esférica; o sea, se puede realizar con regla y compás esféricos.
En el lenguaje de las integrales elípticas, la función inversa F–1 de F se llama amplitud. Se quiere que la calculadora tome dos amplitudes positivas 
 y produzca las amplitudes
y produzca las amplitudes  de la suma y
de la suma y  de la diferencia. Sin pérdida de generalidad se asume que
de la diferencia. Sin pérdida de generalidad se asume que  La construcción va como sigue. Se fija el vértice C en un punto cualquiera de la esfera. Sobre un meridiano cualquiera emanado de C se traza un arco de magnitud Ψ hasta llegar al punto B. Con centro en B y arco constante (radio esférico) Φ se traza una circunferencia sobre la esfera. Luego se traza otro meridiano emanado de C que corte esta circunferencia en los dos puntos A y A'. Entonces,
La construcción va como sigue. Se fija el vértice C en un punto cualquiera de la esfera. Sobre un meridiano cualquiera emanado de C se traza un arco de magnitud Ψ hasta llegar al punto B. Con centro en B y arco constante (radio esférico) Φ se traza una circunferencia sobre la esfera. Luego se traza otro meridiano emanado de C que corte esta circunferencia en los dos puntos A y A'. Entonces,

Se enfatiza el hecho de que no se sabe cuál es cuál, pero de todos modos se obtienen los dos valores distintos. Claro está, se debe garantizar que el triángulo esférico ABC satisfaga La figura 2 ilustra una situación posible.
La figura 2 ilustra una situación posible.
La construcción geométrica anterior es válida porque cada uno de los triángulos ABC y A'BC se puede obtener a partir del otro mediante deformaciones lagrangianas. Además, las deformaciones mencionadas son reversibles.
Ejemplo 2.1. Sean  y
y  . La condición de los senos
. La condición de los senos  implica que
implica que  . El problema se reduce entonces a resolver un triángulo esférico cuando se conocen dos lados y el ángulo opuesto a uno de ellos. Esto se realiza como sigue. El otro ángulo opuesto debe satisfacer
. El problema se reduce entonces a resolver un triángulo esférico cuando se conocen dos lados y el ángulo opuesto a uno de ellos. Esto se realiza como sigue. El otro ángulo opuesto debe satisfacer

Por tanto, hay dos soluciones posibles, a saber:  y
y  Puesto que el ángulo restante es tal que
Puesto que el ángulo restante es tal que

se obtienen los valores  y
y  La ley de los senos, de nuevo, produce
La ley de los senos, de nuevo, produce  y
y  Es fácil verificar que estos valores hacen verdaderas las identidades de Lagrange correspondientes.
Es fácil verificar que estos valores hacen verdaderas las identidades de Lagrange correspondientes.
El procedimiento geométrico se puede repetir para determinar otras sumas. No sobra insistir en que se trata del procedimiento geométrico y no del analítico basado en las funciones trigonométricas. Este último conduce a complicaciones innecesarias que la calculadora analógica resuelve sin dificultad. Por ejemplo, en la expresión para sen A se debe tener sen C ≠ 0. Si c = 0, ya que  el valor Φ = 0 detiene el procedimiento analítico. Sin embargo, la construcción geométrica para
el valor Φ = 0 detiene el procedimiento analítico. Sin embargo, la construcción geométrica para  produce un triángulo degenerado ABC con B = A porque el radio de la circunferencia es nulo. De esta manera, es a todas luces evidente que
produce un triángulo degenerado ABC con B = A porque el radio de la circunferencia es nulo. De esta manera, es a todas luces evidente que  Así mismo, se pensaría que se debe prohibir el caso Φ = Ψ por el problema de la fórmula para
Así mismo, se pensaría que se debe prohibir el caso Φ = Ψ por el problema de la fórmula para  De nuevo, la calculadora produce los resultados correctos μ y ν = 0.
De nuevo, la calculadora produce los resultados correctos μ y ν = 0.
El párrafo anterior ilustra las ventajas relativas de las calculadoras análogas. En primer lugar, su hiperestabilidad: ya que se basan en sistemas físicos, no pueden producir resultados sin sentido. También resuelven ecuaciones diferenciales que no tienen soluciones analíticas y producen resultados continuos, lo cual les da un dominio informático más grande que sus contrapartes digitales. Entre sus desventajas se cuentan los problemas del ruido en las mediciones y las dificultades de miniaturización.
3. TABLAS
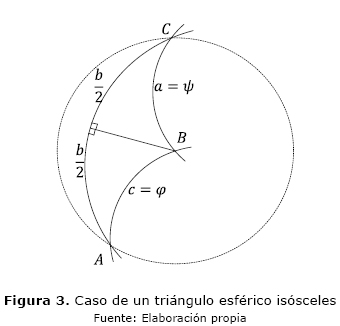
Por el procedimiento geométrico descrito en la sección anterior es posible producir tablas de amplitudes para ángulos igualmente espaciados. Así, si se quiere una tabla en intervalos de (cinco grados), debemos comenzar por la adición con  Se nota que el procedimiento analítico del ejemplo previo no se deja aplicar debido a la singularidad de la función cosecante. Ciertamente, la construcción propuesta conlleva la solución de un triángulo esférico isósceles, el cual debe dividirse en dos triángulos esféricos rectángulos congruentes. La trigonometría esférica [9] enseña cómo resolver estos triángulos con la ayuda de sus relaciones fundamentales, las reglas de Napier y las leyes de los cuadrantes. Sea, como antes,
Se nota que el procedimiento analítico del ejemplo previo no se deja aplicar debido a la singularidad de la función cosecante. Ciertamente, la construcción propuesta conlleva la solución de un triángulo esférico isósceles, el cual debe dividirse en dos triángulos esféricos rectángulos congruentes. La trigonometría esférica [9] enseña cómo resolver estos triángulos con la ayuda de sus relaciones fundamentales, las reglas de Napier y las leyes de los cuadrantes. Sea, como antes, 
Entonces,

El algoritmo mencionado en el párrafo anterior conduce a que

ya que a = c = 5°. La situación se muestra en la figura 3. Un cálculo sencillo prueba que la identidad de Lagrange se verifica. El lector juicioso también podría comprobar la validez de la ley de los senos.
La amplitud obtenida μ se puede tomar ahora como Ψ para adicionarle Φ = 5°. El proceso se puede continuar hasta obtener la tabla siguiente.
A partir de la segunda fila, el proceso se realiza como en el ejemplo de la sección anterior.
4. A MODO DE CONCLUSIÓN
Se han descrito, pues, dos maneras de calcular las amplitudes de la suma y diferencia de dos integrales elípticas de la primera especie. La primera constituye lo que hemos llamado la calculadora analógica de Lagrange. Ella permite obtener resultados rápidos y certeros (hiperestables) mediante una sencilla construcción geométrica sobre una esfera. Sin embargo, las mediciones sobre la superficie introducen errores (ruido) amén de que se hacen más cómodas para tamaños más grandes del radio de la esfera (dificultades de miniaturización). Por esto, los cálculos se han realizado con ayuda de los algoritmos de la trigonometría esférica (segunda manera). Este método constituye la versión digital de la calculadora. Esta vez se enfrentan problemas de programación, puesto que se deben incluir todas las maneras de resolver triángulos esféricos. Entre otras complicaciones, es preciso implementar algoritmos distintos para los triángulos rectángulos y los triángulos oblicuángulos, además de tener en cuenta las llamadas "leyes de los cuadrantes"
En lo anterior se vislumbra la posibilidad de una tercera manera de proceder que comparta las ventajas de las otras dos. Se trataría de realizar las construcciones geométricas sobre la esfera con la ayuda de un instrumento que permita leer y escribir con precisión sobre ella. En concreto, todo el esfuerzo se dedicaría al desarrollo de una especie de transportador esférico que convierta los datos digitales en análogos, y viceversa. Si ello es posible, se lograrían, al mismo tiempo, valores verdaderos y precisos para las amplitudes elípticas.
5. AGRADECIMIENTOS
Este trabajo ha sido financiado parcialmente por la Vicerrectoría de Investigaciones de la Universidad de Medellín y por la Facultad de Ciencias de la Universidad del Tolima. Sus autores agradecen con especial afecto a los estudiantes y profesores que han participado en el Seminario de historia de las integrales elípticas, realizado en Medellín e Ibagué durante los últimos años.
REFERENCIAS
1. T. Freeth, Y. Bitsakis, X. Moussas et al., "Decoding the ancient Greek astronomical calculator known as the Antikythera Mechanism,– NATURE," vol. 444, pp. 587–591, 2006. [ Links ]
2. G.–G. Coriolis, "Sur un moyen de tracer des courbes données par des équations différentielles," Journal de Mathématiques Pures et Apliquées, vol. 1, pp. 5–9, 1836. [ Links ]
3. C. J. De Paz, "Computador análogo: un método de simulación," Facultad de Sistemas e informatica, Guatemala, 1995. [ Links ]
4. T. Beléndez, C. Neipp, and A. Beléndez, "Flexión de una barra delgada empotrada en un extremo: aproximación para pequeñas pendientes.," Revista Brasileira de EnsiNo de Física, vol. 24, no. 4, pp. 399–407, 2002. [ Links ]
5. C. Gutiérrez, and D. González "Campo magnético generado por N bobinas alineadas axialmente.," Ciencia Ergo Sum, vol. 9, pp. 301–307, 2002. [ Links ]
6. A. C. Tamayo, "Geometría y análisis en la historia temprana de las integrales elípticas," Programa de Magister en Educación con énfasis en la Enseñanza de las Matemáticas, Facultad de Educación, Universidad de Antioquia, Medellin, 2006. [ Links ]
7. G. Bellachi, Introduzione storica alla teoria delle funzione ellittice, Firenze: Tipografia di G. Barbèa, 1894. [ Links ]
8. J. L. Lagrange, "Théorie des fonctions analytiques," Euvres (1881), tome neuvième, pp. 127–141: Gauthier–Villars, 1813. [ Links ]
9. F. Ayres, "Chapters 20 and 21," Theory and problems of plane and spherical trigonometry, New York: Schaum Publishing Co., 1954. [ Links ]
10. J. L. Lagrange, "Sur l'intégration de quelques équations différentielles dont les indéterminéees sont séparées, mais dont chaque membre en particulier n'est point intégrable.," Euvres (1868), tome deuxième., pp. 5–33, Paris: Gauthier–Villars, 1766–1769. [ Links ]
11. L. Solanilla, Geometría diferencial de superficies, Medellín: Sello Editorial Universidad de Medellín, 2008. [ Links ]
Recibido: 17/06/2009