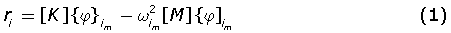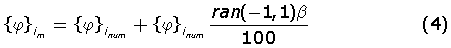Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellín vol.9 no.16 Medellín Jan./June 2010
Detección daño estructural empleando el vector de fuerza residual modificado y el algoritmo Simulated Annealing (SA)
Damage Detection Using the Modified Residual Force Vector and the Simulated Annealing Algorithm (SA)
Óscar Begambre*; Rodrigo Correa**; José Laier***
* Ph. D, profesor auxiliar, Universidad Industrial de Santander. E-mail: ojbegam@uis.edu.co
** Ph. D, profesor titular, Universidad Industrial de Santander. E-mail: crcorrea@uis.edu.co
*** Ph. D, profesor titular, Universidade de São Paulo. E-mail: jelaier@sc.usp.br
Resumen
En este trabajo, el algoritmo Simulated Annealing (SA) es empleado para solucionar el problema inverso de detección de daño en vigas usando información modal contaminada con ruido. La formulación de la función objetivo para el procedimiento de optimización, basado en el SA, está fundamentada en el método de la fuerza residual modificada. El desempeño del SA empleado en este estudio superó el de un algoritmo genético (AG) en dos funciones de prueba reportadas en la literatura internacional. El procedimiento de evaluación de integridad aquí propuesto se confirmó y validó numéricamente empleando la teoría de vigas de Euler-Bernoulli y un Modelo de Elementos Finitos (MEF) de vigas en voladizo y apoyadas libremente.
Palabras clave: Identificación de daños, fuerza residual modificada, algoritmo Simulated annealing.Abstract
In this research, the Simulated Annealing Algorithm (SA) is employed to solve damage detection problems in beam type structures using noisy polluted modal data. The formulation of the objective function for the SA optimization procedure is based on the modified residual force method. The SA used in this research performs better than the Genetic Algorithm (GA) in two difficult benchmark functions. The proposed structural damage-identification scheme is confirmed and assessed using a Finite Element Model (FEM) of cantilever and a free-free Euler-Bernoulli beam model.
Key words: Damage identification, modified residual force, simulated annealing algorithm.
INTRODUCCIÓN
De forma general, la detección de daños en la infraestructura civil consiste en inferir, a través de medidas de la respuesta dinámica del sistema estructural, la posición y severidad del daño presente en puentes o edificios a medida que la estructura se deteriora. Durante los últimos 35 años la investigación en esta área se ha concentrado en el desarrollo de nuevas técnicas no destructivas para evaluar la integridad estructural [1, 2]. Tales métodos hacen parte de lo que se conoce como monitoreo de la salud estructural [3].
En este trabajo, la detección de daño se define como un problema de optimización, en el cual se debe especificar una función objetivo (a ser minimizada / maximizada) en términos de parámetros relacionados con las propiedades físicas de la estructura. Sabiendo que el mínimo de dicha función se obtiene cuando es evaluada con los parámetros verdaderos y empleando el procedimiento SA para estimar esos parámetros, es posible evaluar el estado del sistema, es decir, determinar si el daño ocurrió, dónde y con qué severidad (nivel 3 de detección según Rytter) [4]. En este contexto, vale la pena aclarar que el uso de los métodos clásicos de la programación no lineal para solucionar problemas inversos fuertemente no lineales y con múltiples puntos óptimos como el tratado en este trabajo, tienen el gran inconveniente de ser susceptibles a quedar atrapadas en puntos óptimos locales [5]. Además de la anterior limitación, las técnicas clásicas son altamente sensibles a la presencia de ruidos en los datos experimentales [6]. Esto se debe al hecho de que los gradientes usados dependen explícitamente de los vectores modales medidos y/o de su expansión (cuando se emplean datos modales en la función objetivo); de esta forma, cualquier error en las mediciones o en el modelo corromperá la calidad de los gradientes y comprometerá la calidad de la solución.
Es un hecho conocido que los algoritmos heurísticos necesitan un mayor número de evaluaciones de la función objetivo para encontrar una solución óptima o cuasi óptima cuando se comparan con técnicas basadas en gradientes. Sin embargo, las desventajas de los métodos clásicos mencionadas anteriormente hacen que estas técnicas no puedan ser usadas para atacar el problema de detección de daños vía respuesta dinámica de la estructura. Por otro lado, el empleo de métodos heurísticos para abordar el problema de identificación de daños se presenta como opción promisoria debido a que no requieren ni de continuidad en la definición del problema de optimización ni de la estimación de un punto inicial para garantizar su convergencia (en el problema de identificación de daños, la definición de un punto de partida para comenzar la búsqueda es casi imposible debido a la gran cantidad de opciones existentes). Adicionalmente, están diseñados para buscar soluciones globales o cuasi globales [7, 8].
El empleo de datos modales para detección de daños está estrechamente ligado al análisis modal experimental que se convirtió, a partir de los años 70 en una herramienta muy popular debido a su amplio espectro de aplicaciones, que van desde problemas de acústica hasta la identificación de daños. En este sentido, diversos autores han usado el concepto de la fuerza residual para valorar el daño empleando redes neuronales y algoritmos genéticos [9, 10] y es en este contexto que el presente artículo está inscrito.
1 MÉTODO DE LA FUERZA RESIDUAL MODIFICADA: DEFINICIÓN DEL PROBLEMA DE OPTIMIZACIÓN
La expresión clásica para el vector de fuerza residual rj para el i-ésimo modo de vibración de un sistema con múltiples grados de libertad [11] puede expresarse como:
donde [K] y [M] son las matrices base de rigidez y de masa del modelo de elementos finitos del sistema estructural, y
y 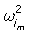 son la i-ésima forma modal del sistema y la i-ésima frecuencia natural determinadas experimentalmente. En esta ecuación, se asume que las frecuencias naturales y las formas modales continúan satisfaciendo la ecuación de valor propio. La ecuación (1) ha empleado para detección de daños, bajo la hipótesis de que el vector rj puede ser construido a partir de los valores exactos de vectores propios y valores propios del sistema. En la práctica, el hecho de que los parámetros modales no pueden ser determinados con completa precisión debido a la inevitable presencia tanto de errores experimentales como de de errores de modelización de las matices [K] y [M] hace que el vector rj pierda información sobre la presencia del daño. Para evitar este problema (la interpretación directa del vector de fuerza residual) se propone la siguiente función objetivo, que debe ser minimizada para poder identificar y cuantificar el daño:
son la i-ésima forma modal del sistema y la i-ésima frecuencia natural determinadas experimentalmente. En esta ecuación, se asume que las frecuencias naturales y las formas modales continúan satisfaciendo la ecuación de valor propio. La ecuación (1) ha empleado para detección de daños, bajo la hipótesis de que el vector rj puede ser construido a partir de los valores exactos de vectores propios y valores propios del sistema. En la práctica, el hecho de que los parámetros modales no pueden ser determinados con completa precisión debido a la inevitable presencia tanto de errores experimentales como de de errores de modelización de las matices [K] y [M] hace que el vector rj pierda información sobre la presencia del daño. Para evitar este problema (la interpretación directa del vector de fuerza residual) se propone la siguiente función objetivo, que debe ser minimizada para poder identificar y cuantificar el daño:
donde
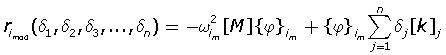
es el i-ésimo vector de fuerza modal residual modificado, [k]j es matriz de rigidez del j-ésimo elemento finito de la estructura, m representa el número de modos medidos, n es el número total de elementos finitos del modelo,  representa la i-ésima frecuencia natural experimental,
representa la i-ésima frecuencia natural experimental, 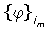 es la i-esima forma modal experimental del sistema, [M] es la matriz de masa del modelo y δj es el j-ésimo parámetro escalar de daño que indica la posición y severidad del mismo. Los valores de δj están contenidos en el intervalo [0,1]. Un valor δj = 0 o menor que 1 indica pérdida total o parcial de la rigidez del respectivo elemento y, por lo tanto, revela si la estructura está o no afectada. Un valor δj = 1 indica que el sistema se encuentra sin daño.
es la i-esima forma modal experimental del sistema, [M] es la matriz de masa del modelo y δj es el j-ésimo parámetro escalar de daño que indica la posición y severidad del mismo. Los valores de δj están contenidos en el intervalo [0,1]. Un valor δj = 0 o menor que 1 indica pérdida total o parcial de la rigidez del respectivo elemento y, por lo tanto, revela si la estructura está o no afectada. Un valor δj = 1 indica que el sistema se encuentra sin daño.
Para este estudio, se creó un conjunto artificial de datos modales experimentales para la ecuación (2) mediante la adición de ruido aleatorio a los datos obtenidos de forma numérica. De esta forma, se definieron γ y β como los ruidos, en términos de porcentaje, introducidos en las frecuencias naturales y las formas modales numéricas, respectivamente. El i-ésimo conjunto de parámetros modales “experimentales” fue generado de la siguiente forma:
donde  y
y 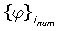 son los parámetros modales numéricos y ran(—1,1) es una función que genera números aleatorios cuyos valores se encuentran en el intervalo [—1,1].
son los parámetros modales numéricos y ran(—1,1) es una función que genera números aleatorios cuyos valores se encuentran en el intervalo [—1,1].
2 EL ALGORITMO SIMULATED ANNEALING
El SA se basa en la analogía entre el proceso físico de enfriamiento lento de sólidos y la solución de problemas de optimización de gran escala con variables continuas y discretas [12-15]. El SA fue propuesto por Kirkpatrick, Gelatti y Vecchi [13] y ha sido empleado en el campo de la física y la cristalografía, para ajustar modelos atómicos de proteínas usando datos experimentales e informaciones químicas [16]. Una de las primeras aplicaciones del SA para determinar el posicionamiento óptimo de sensores y actuadores en estructuras espaciales fue realizada por Salama et al., [17] y su aplicación es relativamente reciente en la disciplina de optimización estructural, donde el objetivo es obtener estructuras con pesos, formas, resistencia óptimos y/o controlar los parámetros de vibración de estos sistemas [18, 19].
El algoritmo SA es esencialmente un procedimiento de búsqueda iterativa aleatoria que permite movimientos de subida (o de descenso) bajo el control de un criterio estocástico. Este criterio es esencial para evitar los óptimos locales. En el corazón del método se encuentra el bien conocido algoritmo de Metropolis et al., [20], que puede ser empleado para resolver problemas con variables continuas. El procedimiento de optimización mediante el SA utilizado en este trabajo puede resumirse en los siguientes pasos:
(1) Definir una función objetivo F (ver ecuación (2)) sobre un espacio n dimensional de variables continuas:
donde
i=1 ⦠n. El problema puede definirse ahora como hallar el Xopt que satisfaga
En la ecuación (6) el estado del sistema esta descrito por el vector de configuración actual(X).
(2) Proponer un mecanismo generador de cambios aleatorios en la configuración actual. Este mecanismo es una forma de transformar X en un nuevo vector de configuración
. El procedimiento para generar estas transiciones puede ser descrito de la siguiente forma: se hace la evaluación de la función en el punto inicial Xj y su valor Fj es guardado. Seguidamente, un nuevo punto,
es seleccionado mediante la variación aleatoria del elemento i de vector Xj , como se muestra en la ecuación (7):
donde λ es un número aleatorio en el intervalo (—1,1), ηi representa un elemento del vector η [15], que es el paso para Xj y xi,
son elementos de Xj y
respectivamente. De esta forma, el valor
de la función es calculado. Si
< Fj,
es aceptado y Xj se iguala a
y el algoritmo realiza un movimiento de descenso. Si
< Fj,la probabilidad que
sea aceptado es dada por el criterio de Metropolis [20] que puede expresarse como:
donde
y T es el parámetro de temperatura, análogo a la temperatura en el proceso físico de atemperamiento (annealing). En la práctica, el valor Pr se compara con P, que es un número aleatorio que pertenece al intervalo (0,1). Si Pr <P, el nuevo punto es aceptado y Xj es igualado a
y, de esta manera, el algoritmo realiza un movimiento de ascenso. En caso contrario,
es rechazado.
Como se sabe, el SA comienza en una temperatura “alta” T0, y, a partir de ahí, una secuencia de puntos Xj es generada hasta que se alcanza el “equilibrio”; esto significa que se ha obtenido una secuencia de puntos Xj cuyo valor promedio de F alcanza un valor estable a medida que j aumenta (a temperatura constante). El mejor punto (mínimo) obtenido se guarda como Xopt.
(3) En este punto, el parámetro de control T debe ser disminuido de acuerdo con una regla de decremento previamente establecida. Al anterior procedimiento se le conoce como programa de enfriamiento [21, 22], y tiene la siguiente forma:
donde h es una constante real (h > 1). Con el valor reducido de T, una nueva secuencia de puntos se genera, comenzando desde Xopt, hasta que el “equilibrio” se logra nuevamente (ver paso 2) y el proceso continúa (paso 3) hasta que el procedimiento finaliza (el criterio de parada es satisfecho, ver paso 4). Es importante resaltar que, para finalizar el programa de enfriamiento, el algoritmo necesita haber realizado un número predeterminado de iteraciones a la misma temperatura. Corana et al., [15] recomiendan escoger el valor máximo entre 100 y N, donde N es el número de variables del problema estudiado.
El valor de la temperatura inicial depende de la función que va a ser optimizada y de la definición del tipo de vecindad empleada en el algoritmo. Un criterio usado para definir este parámetro es la tasa de aceptación, definida como el número inicial de evaluaciones de la función objetivo aceptadas (movimientos de descenso/ascenso) sobre el número total de evaluaciones realizadas (número total de movimientos). En la práctica, un valor de temperatura inicial debe ser tal que el valor de la tasa de aceptación quede entre 0.5 y 0.9. Si el valor de tasa es mayor que 0.9, un porcentaje significativo de evaluaciones se gasta en un estado “fundido”, desperdiciando esfuerzo computacional en una búsqueda equivalente a una exploración aleatoria. Si la tasa de aceptación es menor que 0.5, la probabilidad de que el algoritmo quede preso en un óptimo local aumenta. De lo expuesto anteriormente, queda claro que grandes diferencias en los valores de la función objetivo y/o bajas temperaturas disminuyen la probabilidad de un movimiento de ascenso.
(4) El algoritmo se detiene en un valor pequeño de T para el cual no se puede esperar una mejora en el valor de F. En este trabajo, el criterio de parada se definió mediante un valor de tolerancia de la siguiente forma: si la diferencia entre valores finales de la función objetivo de las p últimas temperaturas y el valor actual de la función es menor que el valor de la tolerancia (tolerancia usada igual a 1E-6), el algoritmo termina.
3 EVALUACIÓN DEL DESEMPEÑO DEL SA: FUNCIONES DE PRUEBA
El potencial y las limitaciones del algoritmo para detección de daño basado en el SA fueron evaluados mediante su aplicación en funciones de prueba que han aparecido recientemente en la literatura especializada. La efectividad del SA (versión propuesta en Corana et al.,) [15] fue evaluada mediante comparación con un algoritmo genético estándar desarrollado por Goldberg D. E [23].
Teniendo en cuenta que el algoritmo estudiado en este trabajo es de naturaleza estocástica, se decidió definir los siguientes criterios para evaluar su desempeño. La desviación estándar y la distancia entre la media y el valor óptimo analítico de las funciones estudiadas fueron usados para medir la precisión y la estabilidad de los métodos. Un método de optimización heurístico es estable si su desviación estándar es baja. El método es preciso si, además de cumplir con la condición anterior, la distancia entre la media de m corridas y el valor óptimo analítico (cuando éste es conocido) es pequeña. Como el problema de detección de daño no es un problema que deba solucionarse en tiempo real, el tiempo de procesamiento no está indicado en los ejemplos presentados; sin embargo, vale la pena mencionar que en todos los casos este tiempo no excedió nunca cien segundos (máquina con procesador Intel® Core™ 2 Duo de 2GHz con 2GB de memoria RAM).
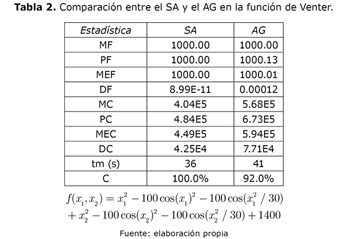
El primer ensayo fue realizado en la función de Brown (B20D) en veinte dimensiones (con mínimo global en (0,...,0) y valor de la función objetivo en ese punto igual a cero) y el segundo en la función de Venter (VS) en dos dimensiones (función con una cantidad considerable de mínimos locales, con su mínimo global localizado en (0,0) y valor de la función igual mil). Los intervalos de búsqueda definidos para la función B20D y VS fueron [—1000, 1000] y [—50, 10], respectivamente. Estas dos funciones constituyen pruebas difíciles para cualquier procedimiento de optimización.
El algoritmo SA fue iniciado como con temperatura inicial T0 = 0,5 para la función B20D y de 50 para la función VS, con constante h = 2 y tolerancia de 1E-6 para las dos funciones. Los cuatro últimos valores de la función fueron monitoreados y usados para terminar la ejecución del algoritmo, como se recomienda en [21]. Finalmente, el número máximo de iteraciones permitidas fue de cuatro millones. Para el algoritmo genético empleado, los parámetros básicos usados se describen a continuación. Se seleccionó una población de 500 individuos, distribuidos de forma aleatoria en el espacio de búsqueda. Con el objetivo de realizar una comparación justa entre el SA y el AG, el número máximo de iteraciones permitidas para el AG también fue de cuatro millones. La probabilidad de mutación Pm fue definida como 0,01 y la probabilidad de cruce Pc fue de 0,5. El mecanismo de selección utilizado fue el de la ruleta. Adicionalmente, en el AG utilizado se implementó el proceso conocido como elitismo, en el cual, el mejor individuo de una generación se pasa a la siguiente sin modificación. El elitismo procura mejorar la velocidad de búsqueda del algoritmo. Cada corrida del algoritmo se realizó mil veces y el mejor valor de la función (MF), el peor valor de la función (PF), el promedio de los valores de la función (MEF), la desviación estándar de los valores de la función (DF), el mejor número de llamadas de la función (MC), el peor número de llamadas de la función PC), el promedio del número de llamadas de la función (MEC), la desviación estándar del número de llamadas de la función (DC), la confianza (C) y tiempo medio de cálculo (tm) son reportados en las tablas 1 y 2. Tabla 1.
Vale la pena resaltar que el valor de C se refiere al número de veces, de un total de mil, que el algoritmo encontró un valor óptimo de la función objetivo dentro de una precisión de 1E-4 del valor analítico. Como se puede ver en las tablas 1 y 2, el desempeño del AG fue inferior al del SA en la dos funciones de prueba (se debe recordar, que en un escenario real de daño, no se sabe con anticipación su localización y, por lo tanto, el algoritmo que presente mayor C tendrá obvia ventaja). En este contexto, en el trabajo presentado por Rao et. al. [10], no se realiza un análisis estadístico del comportamiento del AG empleado, por lo tanto, no se puede concluir sobre su confiabilidad y estabilidad en el problema de detección de daño. Por otro lado, como se demuestra de forma clara en el estudio presentado por Guo y Li [24] es difícil para el AG básico solucionar el problema de identificación de daños (en vigas) empleando datos modales. Finalmente, debido a las razones expuestas arriba, y a que el SA no se ha empleado con funciones basadas en datos modales (en este caso, el vector de fuerza residual), se decidió continuar trabajando con el SA en los problemas de detección de daño presentados en la próxima sección.
4 DETECCIÓN DE DAÑO USANDO EL SA: EJEMPLOS NUMÉRICOS
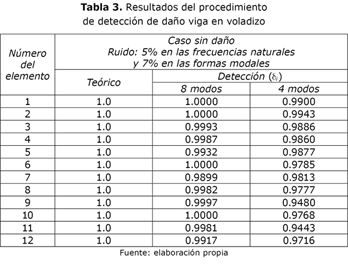
Teniendo en cuenta los resultados y comentarios de la sección anterior, se procedió a emplear el SA en casos de detección de daño simulados numéricamente. Los casos considerados aquí son una viga en voladizo y una viga en condición libre modeladas con la teoría de Euler â Bernuolli. Cada una de las vigas fue discretizada empleando 12 elementos finitos unidimensionales, conteniendo cada uno 24 y 26 grados de libertad, respectivamente. Las vigas se muestran en la y sus propiedades son: área de sección transversal 4E-4 m2, densidad 7800 kg/m3, longitud 0.8 m, módulo de elasticidad 200 GPa, momento de inercia 2.38E-8 m4. Para cada viga dos situaciones fueron estudiadas: (1) las vigas no sufrieron ningún daño y los parámetros modales fueron contaminados con ruido, como se indica en las tablas 3 y 5. (2) El daño fue introducido parcialmente en los elementos 4 y 8 con una severidad de 20% y 15%, respectivamente (reducción de rigidez) con ruido de 5% en las frecuencias naturales y de 7% en las formas modales y empleando 4, 5 y 8 modos en la identificación, como se puede ver en las tablas 4 y 6. Para cada caso, el punto inicial del SA fue escogido de forma aleatoria y se realizaron 10 corridas del algoritmo.
En los ejemplos presentados, se asume que los grados de libertad rotacionales no fueron medidos experimentalmente. En esta situación, el modelo numérico fue condensado empleando el método de Kidder [25] para obtener la función objetivo (ver ecuación 2). De esta forma, el vector de fuerza residual original pierde su significado inicial pero aún permite, como se verá adelante, la detección de daño. Los resultados de los ejemplos se presentan en las tablas 3, 4, 5 y 6. Los parámetros básicos para el SA fueron los siguientes: temperatura inicial T0 = 50 constante para el programa de enfriamiento h = 2, tolerancia ε = 1E-6, con el criterio de terminación indicado anteriormente (funciones de prueba). En las tablas 3, 4, 5 y 6 se informa el resultado de la mejor corrida, así como los datos estadísticos pertinentes.
El número total de evaluaciones de la función objetivo hasta que el criterio de parada terminó la búsqueda fue el siguiente (para la mejor corrida): 6001 en el caso (1) y 9601 en el caso (2) para la viga en voladizo, 8401 en el caso (1) y 10081 en el caso (2) para la viga libre. En ningún caso el número de llamadas a la función objetivo excedió a 16000. Por otro lado, las desviaciones estándar de los valores de la función objetivo fueron siempre menores a 1E-6, lo que indica que el procedimiento es estable.
En los casos contaminados con ruido, mostrados en las tablas 4 y 6, se puede apreciar que la mejor identificación del daño se obtuvo cuando fueron empleados ocho modos y que una detección aceptable fue lograda empleando solo cuatro modos. Cuando el número de modos usados fue tres, el procedimiento de detección aquí propuesto realizó una identificación errónea del daño. En los casos sin daño, el esquema de detección funciono bien con solo cuatro modos. El SA, como fue implementado en este trabajo, mostró una velocidad de convergencia satisfactoria y parece indicado para la labor de detección de daños empleando modelos.
5 CONCLUSIONES
El procedimiento de detección de daño basado en el SA presentado aquí permite la identificación apropiada de los elementos afectados en las vigas estudiadas cuando la mínima degradación de rigidez del elemento es 15%. La detección arrojó buenos resultados con los escenarios de daño contaminados con ruido y empleando solo los cuatro primeros modos de vibración (ver tablas 3 a 6). La baja estabilidad y precisión del AG empleado en este trabajo lo hacen inapropiado para la tarea de detección de daño. Por otro lado, el buen comportamiento de SA en las pruebas realizadas lo hace un fuerte candidato para futuras aplicaciones prácticas de detección de daño en estructuras.
AGRADECIMIENTOS
El primer autor desea agradecer a la Vicerrectoría de Investigación de la Universidad Industrial de Santander por el apoyo económico dado a esta investigación. J. E. Laier agradece al CNPQ, Brasil por el apoyo financiero a este trabajo.
REFERENCIAS
1. P. E. Carden, y P. Fanning, “Vibration Based Condition Monitoring: A Review,” Structural Health Monitoring, vol. 3, no. 4, pp. 355-377, 2004. [ Links ]
2. D. Barke, y W. K. Chiu, “Structural Health Monitoring in the Railway Industry: A Review,” Structural Health Monitoring, vol. 4, no. 1, pp. 81-93, 2005. [ Links ]
3. P. C. Chang et al., “Health Monitoring of Civil Infrastructure: Review paper,” Structural Health Monitoring, vol. 2, no. 3, pp. 257-267, 2003. [ Links ]
4. A. Rytter, “Vibration Based Inspection of Civil Engineering,” University of Aalborg, Aalborg, Denmark, 1993. [ Links ]
5. S. Y. Lee, y S. H. Wooh, “Detection of stiffness reductions in laminated composite plates from their dynamic response using the microgenetic algorithm,” Comput Mech, vol. 36, no. 4, pp. 320-330, 2005. [ Links ]
6. F. M. Hemez et al., “On The efficiency of model updating via genetic algorithm for structural damage detection,” en 36th AIAA/ASME/ASCE/AHS/ASC Structures, structural dynamics and materials conference New Orleans, USA, 1995, pp. 2792-2801. [ Links ]
7. J. F. Schutte, y A. A. Groenwold, “Sizing desing of truss structures using particle swarm particle,” Structural and Multidisciplinary Optimization, vol. 25, no. 4, pp. 261-269, 2003. [ Links ]
8. S. M. Bland, y R. K. Kapania, “Damage Identification of Plate Structures using Hybrid Genetic-Sensitivity approach,” AIAA Journal, vol. 43, no. 2, pp. 439-442, 2004. [ Links ]
9. T. Marwala, y H. E. M. Hunt, “Fault identification using finite element models and neural networks,” Mechanical systems and signal processing, vol. 13, pp. 475-490, 1999. [ Links ]
10. M. A. Rao et al., “Damage detection in vibrating bodies using genetic algorithms,” Computers and structures, vol. 82, no. 11-12, pp. 963-968, 2002. [ Links ]
11. J. M. Ricles, y J. B. Kostmatka, “Damage detection in elastic structures using vibratory residual forces and weighted sensitivity,” AIAA Journal, vol. 30, no. 9, pp. 2310-2316, 1992. [ Links ]
12. T. Y. Chen, y J. J. Su, “Efficiency improvement of simulated annealing in optimal structural design,” Advances in Engineering Software, vol. 33, pp. 675-680, 2002. [ Links ]
13. S. Kirkpatrick et al., “Optimization by simulated annealing,” Science, vol. 220, no. 4598, pp. 671-680, 1983. [ Links ]
14. V. Cerny, “Thermodynamical approach to the traveling salesman problem: An efficient simulation algorithm,” J. Opt. Theory Appl, vol. 45, no. 1, pp. 41-51, 1985. [ Links ]
15. A. Corana et al., “Minimizing multimodal functions of continuous variables with the Simulated Annealing Algorithm,” ACM Transactions on Mathematical Software, vol. 13, no. 3, 1987. [ Links ]
16. A. T. Brunger, “Simulated Annealing in Crystallography,” Annual Review of Physical Chemistry, vol. 42, pp. 197-223, 1991. [ Links ]
17. M. Salama et al., “Optimal placement of excitations and sensors by simulated annealing,” en Langley Research Center, Recent Advances in Multidisciplinary Analysis and Optimization NASA CP-3031, 1990, pp. 1441-1458. [ Links ]
18. K. Genoves et al., “Improved global-local simulated annealing formulation for solving non-smooth engineering optimization problems,” International Journal of solids and Structures, vol. 42, no. 1, pp. 203-237, 2005. [ Links ]
19. S. Ziaei-Rad, “Finite element model updating of rotating machinery using different optimization techniques,” Iranian Journal of Technology, Transaction B, Engineering, vol. 29, no. B6, pp. 569-585, 2005. [ Links ]
20. N. Metropolis et al., “Equations of state calculations by fast computing machines,” Journal of Chemical Physics, vol. 21, no. 6, pp. 1087-1092, 1953. [ Links ]
21. M. Lundy, y A. Mees, “Convergence of an annealing algorith,” Mathematical Programming, vol. 34, no. 1, pp. 111-124, 1986. [ Links ]
22. P. J. M. Van Laarhoven et al., “Job shop scheduling by simulated annealing,” Operations Research, vol. 40, no. 1, pp. 113-125, 1992. [ Links ]
23. D. E. Goldberg, Genetic algorithm in search, optimization and machine learning, Reading, PA, USA: Addison-Wesley Professional, 1989. [ Links ]
24. H. Y. Guo, y Z. L. Li, “A two-stage method to identify structural damage sites and extents by using evidence theory and micro-search genetic algorithm,” Mechanical Systems and Signal Processing, vol. 23, no. 3, pp. 769-782, 2009. [ Links ]
25. R. L. Kidder, “Reduction of Structural Frequency Equations,” AIAA Journal, vol. 11, no. 6, pp. 892, 1973. [ Links ]
Recibido: 15/04/2009
Aceptado: 07/05/2010