Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista Ingenierías Universidad de Medellín
Print version ISSN 1692-3324On-line version ISSN 2248-4094
Rev. ing. univ. Medellín vol.10 no.18 Medellín Jan./June 2011
Un análisis de la dinámica de largo plazo de la UVR
Analysis of the long term dynamics of the constant value unit
Juan David Velásquez H.*; Soraida Aguilar V.**
* Autor para correspondencia. Doctor en Ingeniería-Área Sistemas Energéticos, Universidad Nacional de Colombia, sede Medellín, Colombia, 2009; magíster en Ingeniería de Sistemas, Universidad Nacional de Colombia, sede Medellín, Colombia, 1997; ingeniero civil, Universidad Nacional de Colombia, 1994. Profesor asociado de la Escuela de Sistemas, Facultad de Minas, Universidad Nacional de Colombia, sede Medellín. Correo electrónico: jdvelasq@bt.unal.edu.co.
** Magíster en Ingeniería de Sistemas, Universidad Nacional de Colombia, Sede Medellín, Colombia, 2009; Ingeniera administradora, Universidad Nacional de Colombia, Sede Medellín, Colombia, 2005. Correo electrónico: soraguilar@gmail.com
Resumen
Los modelos de Box y Jenkins han sido ampliamente usados para la modelación y el pronóstico de muchas variables económicas y financieras. En este artículo se explora la utilización de dicha metodología como una alternativa para el análisis de la dinámica de largo plazo del UVR. El modelo SARIMA resultante fue aceptado después de aplicarle una serie de pruebas estándar de diagnóstico; lo cual dio como resultado que el modelo se ajusta de manera adecuada a los datos, y que la precisión del pronóstico extrapolativo se ajusta estadísticamente bien al representar los patrones ciclos y de largo plazo.
Palabras clave: modelos arima; series de tiempo; unidad de valor real, diferenciación, integración.Abstract
Box and Jenkins models have been used for modeling and forecasting of many economic and financial variables. In this article, that methodology was used as an alternative to analyze the long- term dynamics of the constant value unit. The final model was accepted after applying several standard tests of diagnostic. The SARIMA model was accepted after having used an amount of standard diagnostic tests, as result of it, the model fit well to the data, and explorative prediction accuracy is acquired when it represents the cycle patterns and for long term.
Key words: arima models, time series, constant value unit, difference, integration.
INTRODUCCIÓN
La modelación y predicción de series temporales ha sido un problema al que constantemente le apuestan los expertos en econometría, debido a la alta complejidad en la representación de los datos y en la reproducción de predicciones tanto de largo como de corto plazo. Los modelos ARIMA, postulados por Box y Jenkins [1], se han utilizado ampliamente para diversas aplicaciones en el campo económico, rompiendo de esta manera con el paradigma de que la variable independiente era únicamente explicada por sus variables regresoras, para "permitir que la información hable por sí misma" por medio de sus valores pasados o rezagados, y por los términos estocásticos del error.
Actualmente, los referentes de indexación juegan un papel predominante en la economía debido a la función actualizadora de la misma. El UVR posee la característica de ser un actualizador económico para créditos hipotecarios y fue establecido en 1999 en reemplazo del antiguo UPAC; dado esto, es de interés pronosticar la serie mensual del UVR, ya que si bien se pueden transar créditos de vivienda teniendo en cuenta dicho valor, no son las únicas operaciones de largo plazo que se pueden efectuar bajo ésta modalidad. No obstante, cabe anotar que no se han encontrado evidencias sobre la realización de estudios en el modelado del UVR, y que por tanto, el objetivo de este artículo es analizar su dinámica de largo plazo.
En este artículo se contribuye al desarrollo de un modelo univariado basado en el modelo Seasonal ARIMA del UVR, modelo comúnmente conocido como SARIMA; este reporte se encuentra organizado de la siguiente manera: la descripción de la información utilizada y la metodología de modelado son presentadas en la sección 1; el modelo obtenido, los resultados de las pruebas estadísticas de especificación, y su discusión se presentan en la sección 2; finalmente, se exponen las conclusiones más relevantes.
1 Datos y metodología
1.1 Información utilizada y análisis preliminar
La Unidad de Poder Adquisitivo Constante (UPAC) es conocida como una unidad de cuenta que permitió realizar operaciones de crédito hipotecario a largo plazo a través de ajustes de valor, de acuerdo con la capacidad adquisitiva de la moneda legal. En el diseño de este instrumento financiero, se concibió que su valor se modificará de acuerdo con la variación resultante del promedio del Índice Nacional de Precios al Consumidor (IPC); sin embargo, según Cuartas [2],esto fue sólo en teoría, ya que después se adicionó una corrección basada en la tasa de interés de los depósitos a término fijo (DTF) del mercado para determinar el valor diario dela UPAC en pesos. Dicha corrección monetaria poseía grandes falencias como la ausencia de normas que regularizaran la competencia entre las corporaciones financieras, debido a que cada entidad era autónoma para proponer su propio sistema de amortización, haciendo que el cliente comparara entre ofertas. Otro problema dela UPAC era el incurrimiento en la capitalización de los intereses (interés sobre interés) por estar atada al DTF, ya que se violaba la ley de vivienda en la cual se prohibía explícitamente dicha capitalización. Tal irregularidad no permitía al inversionista la conservación del valor del bien en el tiempo, ya que el monto de la deuda crecía vertiginosamente debido a la capitalización de intereses; esto demostró que la UPAC no era coherente con la filosofía para la cual había sido creada.
Por tal motivo, el gobierno se vio en la obligación de crear el sistema UVR (Unidad de valor real) para reemplazar el antiguo sistema UPAC. Al igual que este último, el sistema UVR tiene como función la regulación del crédito hipotecario para la financiación individual de la vivienda a largo plazo con un método de amortización homogéneo. La UVR se decretó bajo la ley 546 de 1999 como un instrumento normativo ante el comportamiento inconstitucional del sistema UPAC, lo que conllevó a la reliquidación de algunos créditos hipotecarios que estaban vigentes, en términos de UVR o en pesos.
Por otra parte, la ley 546 de 1999 de Financiación de Vivienda incluyó nuevos instrumentos de captación a largo plazo para las entidades financiadoras, tales como bonos hipotecarios y titularizaciones, empleando recursos de largo plazo para las colocaciones de largo plazo, con el fin de generarle solidez al sistema. Esta unidad de cuenta refleja el poder adquisitivo de la moneda, con base en la variación del Índice de Precios al Consumidor que es lo que se conoce como inflación, y permite, así, ajustar el valor de los créditos en el tiempo de acuerdo con el costo de vida del país.
Para el cálculo de la UVR, se tiene en cuenta la variación mensual del índice de precios al consumidor para el mes calendario inmediatamente anterior al mes de inicio del período de cálculo; esto implica que durante los meses en los cuales estacionalmente la inflación es alta, la UVR tendrá un reajuste mayor que el que se presenta en meses de baja inflación. Esto es importante, porque para los usuarios de créditos hipotecarios es más conveniente una UVR mensual que refleje exactamente la inflación de ese período y no una inflación histórica rezagada que podría ser mucho más alta que la variación mensual; igualmente, si se compara la UVR con la reducción de la inflación (reducción de los ingresos reales), una UVR calculada con la inflación mensual permite que esa disminución de la inflación se vea reflejada inmediatamente en el descenso de los costos financieros de las obligaciones contraídas, en tanto que, una unidad calculada con el IPC anual mostraría un crecimiento más acelerado del valor dela UVR.
Bajo estas condiciones se establece la UVR como un referente legalmente viable al lado de otros índices que cumplen una función idéntica como son: el precio del oro, la cotización del dólar u otras divisas, o el mismo IPC. Tanto los particulares como las entidades financieras vigiladas por la Superintendencia pueden expresar los montos de las operaciones bilaterales que se celebren, diferentes a créditos destinados a la adquisición de vivienda, en unidades de valor real (UVR); ello se debe a que en el parágrafo del artículo 38 de la ley 546 de 1999se faculta a las entidades financieras para re denominar las cuentas de ahorro y demás pasivos en términos UVR, si el deudor así lo elige.
Para el análisis de largo plazo de la UVR, se seleccionó para su estudio, la serie obtenida como el valor en el último día de cada mes para el periodo comprendido entre enero de 2000 y enero de 2007.
1.2 Modelo autorregresivo y su proceso de especificación
Los modelos autorregresivos (AR) fueron inicialmente introducidos por Yule [3] y luego generalizados por Walker [4], para los cuales se define la autorregresión como una forma de medida de la relación entre la variable dependiente con la variable independiente, donde esta última se encuentra relacionada con los valores pasados de la serie. De ahí que un modelo autorregresivo expresa su pronóstico como una función de los valores pasado de la serie.
De otro lado, los modelos de medias o promedios móviles (MA) fueron inicialmente utilizados por Slutzky [5], quien argumentaba que para una serie temporal se puede definir la media móvil de orden Q como el promedio de los valores pasados de las Q observaciones. Sin embargo, en el trabajo de Wold [6] se propusieron los fundamentos teóricos del proceso combinado ARMA en tres direcciones: la identificación eficiente, un procedimiento de estimación (para AR, MA, y ARMA), y la extensión de los resultados incluyendo series de tiempo estacionarias; su extensión incluye los procesos no estacionarios (ARIMA), para los cuales, la modelación de la componente MA en un proceso ARIMA significa que el valor de la serie temporal en el tiempo t es influenciado por un término del error recurrente y (posiblemente) por términos del error en el pasado.
De igual modo, los modelos autorregresivos integrados de media móvil (ARIMA), propuestos por Box y Jenkins [1], han sido estudiados ampliamente, y para éstos se plantean tres fases en su proceso de especificación: identificación, estimación-validación, y aplicación. En la etapa de identificación se consideran los autocorrelogramas tanto simples como parciales; si dichos autocorrelogramas indican no estacionariedad, la serie temporal debe ser convertida en una serie estacionaria a través de la transformación que sea requerida. Una vez la serie es transformada, se procede a estudiar la presencia de irregularidades para la identificación tentativa del modelo. Posteriormente, se analiza la presencia de patrones estacionales y se determina su período, procedimiento que se apoya en los gráficos de los espectros de frecuencias de la serie de datos. En la etapa de estimación y validación de los coeficientes del modelo tentativo, los parámetros son estimados adaptando la función del modelo a los datos de la serie temporal y minimizando un criterio para los residuales del error.
Una vez se validan y se analizan los resultados, se comprueba si el ajuste del modelo a los datos es estadísticamente adecuado, esto es, se valida que los residuales (diferencia del valor observado y el valor pronosticado por el modelo) sean normales e incorrelacionados y que la varianza sea homocedástica.
El modelo general que se propone en este artículo se especifica en la ecuación (1),y es una combinación del modelo autorregresivo (AR) y de media móvil (MA), donde el primero modela la influencia de los valores pasados de la serie (yt hacia atrás), y el MA modela la influencia del ruido en valores anteriores de la serie (at hacia atrás).El modelo definido en la ecuación (1) incorpora un operador de diferenciación simple que permite dar cuenta de la tendencia de largo plazo, y un operador de diferenciación estacional cuya función es extraer la componente cíclica de período anual presente en la serie estudiada. Este modelo es usualmente conocido como SARIMA (Seasonal ARIMA).
Una vez se ha defino el tipo de modelo a utilizar, y después de que los coeficientes han sido estimados, se procede a restablecer las características originales de la serie de datos, esto es, se deshacen las transformaciones iniciales que han sido efectuadas para estabilizar la serie e inducir estacionariedad. A ese proceso inverso se le denomina en general integración.
1.3 Caracterización de la serie
El primer paso para identificar el modelo es considerar la serie del UVR mensual para el período comprendido entre enero de 2000 y enero de 2007 (figura 1). En la figura 2 se resumen las propiedades estadísticas de la serie transformada usando la función logaritmo natural. La columna (a) corresponde al gráfico el autocorrelograma simple; la (b) al gráfico del autocorrelograma parcial; la (c) al espectro de energía; y la (d) al histograma.
Los aucorreologramas simple y parcial muestran un patrón típico de las series no estacionarias que siguen un proceso de raíces unitarias. Una rápida inspección visual (figura 1) revela una clara tendencia creciente de largo plazo y un patrón cíclico estacional. Para determinar si efectivamente la serie estaba integrada, se aplicaron varios contrastes de raíces unitarias a los datos; las pruebas de Dickey y Fuller [7] (cuyo estadístico toma el valor de 0.3, p-crítico > 1%), Kwiatkowski, Phillips, Schmidt, y Shin [8] (cuyo estadístico toma el valor de -1.25, p-crítico < 1%), y de Schmidt y Phillips [9] (cuyo estadístico toma el valor de -2.04, p-crítico < 1%) confirman la hipótesis de que la serie está integrada y se debe transformar usando una diferenciación simple para eliminar la tendencia, esto es, aplicar el factor (1-B) a la serie para transformarla.
En la segunda fila de la figura 2, se presentan las propiedades de la serie diferenciada (esto es, para , donde es el logaritmo de la UVR). El autocorrelograma simple y el espectro de energía señalan claramente la presencia de un patrón estacional de ciclo anual, el cual también se aprecia en la figura 1(b). Dicho patrón estacional presenta un valor máximo aproximadamente en mayo y un mínimo en enero. Esto señala que para hacer la serie estacionaria es necesario aplicar el operador de diferenciación estacional de período 12 notado como (1-B12). La varianza es aproximadamente constante en el tiempo, lo que sugiere que no es necesario un procesamiento adicional para compensar las variaciones de los datos. Las propiedades de la serie finalmente obtenida (tercera fila de la figura 2), después de aplicar los operadores de diferenciación simple y estacional, señalan que el proceso es estacionario y no es necesario realizar ningún otro paso adicional.
2 Resultados obtenidos y discusión
A continuación se exponen los resultados que se obtuvieron después de aplicar el proceso de especificación del modelo ARIMA descrito en las secciones previas. Cabe resaltar que la serie se encuentra disponible en la página web del Banco de la República de Colombia.
El análisis de los autocorrelogramas simple y parcial de la serie diferenciada (tercera fila de la figura 2) indican que la serie puede ser aproximada con un modelo ARMA, en el cual son significativos los rezagos 2 y 8 para la componente autorregresiva, y 1, 3, 11 y 12 para la componente de medias móviles. En el espectro de energía (figura 2c), se evidencia que la serie presenta altas concentraciones de frecuencias. En el histograma (figura 2d), se observa que los datos de la serie siguen una distribución aproximadamente normal.
Seguidamente, se realizó la estimación de los parámetros del modelo autorregresivo y de medias móviles, para los cuales se estimaron: el valor que toma cada parámetro, su error estándar y el estadístico t . La validación de los parámetros se llevó a cabo a través de la evaluación del estadístico de prueba t de cada uno, respecto a un nivel de confianza del 95%. De esta forma, se seleccionaron aquellos parámetros con |t| > 1.65. En la tabla 1 se presentan los parámetros del modelo final; igualmente, se resumen algunos de los estadísticos que miden el ajuste entre la serie y el modelo; U-Theil es el estadístico U propuesto por Theil [10] que indica la reducción de varianza del modelo actual respecto a un modelo de paseo aleatorio; dicho estadístico muestra que hay una reducción del 45% respecto al paseo aleatorio. El estadístico R2 corrobora la apreciación visual de ajuste del modelo a los datos. De acuerdo con los contrastes de normalidad utilizados, los residuales siguen una distribución normal.
En la figura 3, se resumen las principales propiedades estadísticas de los residuales; la función de autocorrelación simple (FAC) y el espectro de energía indican que los residuales parecen ser incorrelacionados; además, el histograma indica que son aproximadamente normales. En la tabla 1 se reportan las pruebas de normalidad de Jarque y Bera [11] y Lin y Muldhokar [12]; ellas indican que los residuales son normales. Por otra parte, en la tabla 2 se presentan las pruebas de correlación de Box y Pierce[13], Ljung y Box [14] y McLeod y Li [15], respectivamente, las cuales permiten concluir que los residuales son incorrelacionados, y que no se evidencia la presencia de componentes no lineales en los datos. ARCH es la prueba de heterocedasticidad de Engle [16]; dicho estadístico evidencia que los residuales son homocedásticos.
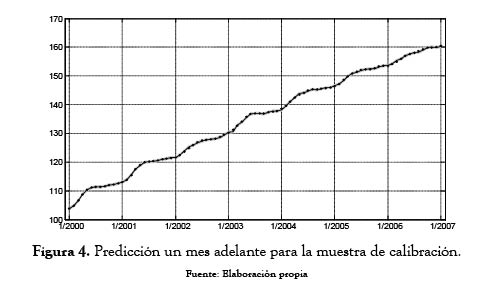
En la figura 4 se presentan los valores pronosticados para el UVR propuesto. Las observaciones se representan por puntos en dicha figura; el pronóstico del modelo es representado por una línea continua; y finalmente, los intervalos de confiabilidad del 95% para el pronóstico son demarcados por la región sombreada. En la tabla 1 se encuentran los estadísticos de ajuste del modelo; estos indican adicionalmente, que fuera de que el modelo captura todas las componentes cíclicas y de tendencia de largo plazo de la serie, igualmente presenta errores bajos en la predicción.
En la figura 5 se presenta el pronóstico determinístico extrapolativo del modelo. En dicho pronóstico yT + 1fue calculado con base en la información histórica disponible hasta yT. Para calcular yT + 2se utiliza la información disponible hasta yT y el pronóstico para yT + 1; este proceso se aplica recursivamente durante la ventana de predicción deseada. Se puede observar en la figura que la serie reproduce adecuadamente los ciclos anuales de la serie y su tendencia de largo plazo.
3 Conclusiones
La metodología desarrollada por Box y Jenkins establece un marco formal y riguroso para el análisis de series temporales. En este artículo se realiza el análisis de la dinámica de largo plazo de la serie del UVR mediante la especificación de un modelo SARIMA, el cual ha sido aceptado después de aplicarle un grupo de pruebas de especificación y aceptación basadas en criterios estadísticos. Este modelo fue desarrollado con un número de observaciones existentes desde su fecha de creación.
Las principales conclusiones a las que se llega con los resultados obtenidos están relacionadas con que el modelo SARIMA hallado representa adecuadamente la dinámica del UVR. Adicionalmente, es interesante ver cómo en la precisión del pronóstico no se observan variaciones después de 12 meses; indica esto, que el pronóstico extrapolativo representa de manera confiable los patrones cíclicos y de largo plazo de la serie del UVR, hecho que puede ser validado a través de inspección visual en la figura 5.
El análisis de la dinámica de largo plazo del UVR puede ser utilizado no solamente para evaluar créditos hipotecarios de largo plazo, sino que puede ser usado para valorar aquellas deudas puedan ser contraídas al tener en cuenta su comportamiento y su tendencia.
REFERENCIAS
[1] G. Box, y G. M. Jenkins, Time-Series analysis, forecasting and control, 2 ed., San Francisco: Holden-Day, 1976, 575 p. [ Links ]
[2] V. Cuartas, "Las unidades de valor real UVR," Revista de Estudios Financieros de la Universidad de Medellín, vol. junio 2000, pp. 8-11, 2000. [ Links ]
[3] G. U. Yule, "Why do we sometimes get nonsense-correlations between time series? A study in sampling and the nature of time series," Journal of the Royal Statistical Society, vol. 89, no. 1, pp. 1-63, 1926. [ Links ]
[4] A. M. Walker, "On the periodicity in series of related terms," Proceedings of the Royal Society of London, vol. 131, no. 818, pp. 518-532, 1931. [ Links ]
[5] E. Slutzky, "The summation of random causes as the source of cyclic processes," Econometrica, vol. 5, no. 2, pp. 105-146, 1937. [ Links ]
[6] H. Wold, A study in the analysis of stationary time series, 2 ed., Stockholm: Almquist & Wiksell, 1954, 236 p. [ Links ]
[7] D. Dickey, y W. Fuller, "Distribution of the estimators for autoregressive time series with a unit root," Journal of American Statistical Association, vol. 74, no. 366, pp. 427-431, 1979. [ Links ]
[8] D. Kwiatkowski et al., "Testing the null hypothesis of stationarity against the alternative of a unit root : How sure are we that economic time series have a unit root?," Journal of Econometrics, vol. 54, no. 1-3, pp. 159-178, 1992. [ Links ]
[9] P. Schmidt, y P. Phillips, "LM tests for a unit root in the presence of deterministic trends," Oxford Bulletin of Economics and Statistics, vol. 54, no. 3, pp. 257-287, 1992. [ Links ]
[10] H. Theil, Economics and Information Theory, Amsterdam: North-Holland, 1967, pp. 488 p. [ Links ]
[11] C. Jarque, y A. Bera, "Efficient tests for normality, homoscedasticity and serial independence of regression residuals," Economic Letters, vol. 6, no. 3, pp. 255-259, 1980. [ Links ]
[12] G. S. Lin, y C. T. Mudholkar, "A Simple Test for Normality against Asymmetric Alternatives," Biometrika, vol. 67, no. 2, pp. 455-461, 1980. [ Links ]
[13] G. Box, y D. Pierce, "Distribution of residual correlations in autoregressive-integrated moving average time series models," Journal of American Statistical Association, vol. 65, no. 332, pp. 1509-1526, 1970. [ Links ]
[14] L. Ljung, y G. Box, "On a measure of lack of fit in time series models," Biometrika, vol. 66, no. 2, pp. 67-72, 1978. [ Links ]
[15] A. McLeod, y W. Li, "Diagnostic checking ARMA time series models using squared residual autocorrelations," Journal of Time Series Analysis, vol. 4, no. 4, pp. 269-273, 1983. [ Links ]
[16] R. Engle, "Autoregressive conditional heterocedasticity with estimates of the variance of United Kingdom inflations," Econometrica, vol. 50, no. 4, pp. 987-1007, 1982. [ Links ]
Recibido: 11/11/2009
Aceptado: 25/02/2011













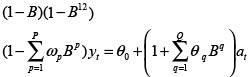 (1)
(1)