ARTÍCULOS

ALGORITMO FONÉTICO PARA DETECCIÓN DE CADENAS DE TEXTO DUPLICADAS EN EL IDIOMA ESPAÑOL

PHONETIC ALGORITHM TO DETECT DUPLICATE TEXT STRINGS IN SPANISH

Iván Amón^*; Francisco Moreno^**; Jaime Echeverri^***

* Facultad de Ingeniería Informática y Telecomunicaciones; Grupo de Investigación GIDATI; Universidad Pontificia Bolivariana–Medellín Colombia; MSc Ingeniero de Sistemas, docente titular UPB. E-mail: ivan.amon@upb.edu.co.
** Escuela de Sistemas; Universidad Nacional de Colombia–Medellín; PhD Ingeniero de sistemas, docente investigador, UN. E-mail: fjmoreno@unal.edu.co.
*** Facultad de Ingeniería; Ingeniería de Sistemas, Universidad de Medellín; PhD( c ) Ingeniería de Sistemas, docente investigador, UN. E-mail: jaecheverri@udem.edu.co.

Recibido: 31/08/2011
Aceptado:: 24/05/2012

RESUMEN

Con frecuencia datos que deberían estar escritos de forma idéntica no lo están debido a errores ortográficos y tipográficos, variaciones en el orden de las palabras, uso de prefijos y sufijos, entre otros. Las técnicas fonéticas para detección de duplicados no están orientadas al idioma español, lo que dificulta la identificación y corrección de problemas como errores ortográficos en textos escritos en este idioma. En este artículo de investigación se propone un algoritmo denominado PhoneticSpanish para la detección de cadenas de texto duplicadas el cual considera la presencia de errores ortográficos en el idioma español. El algoritmo propuesto se comparó con nueve técnicas para la detección de duplicados. Los resultados del algoritmo fueron satisfactorios ya que se obtuvieron mejores resultados que las otras técnicas y evidencian oportunidades para mejorar el análisis de información en el idioma español.

PALABRAS CLAVE

Limpieza de datos, calidad de datos, detección de duplicados, funciones de similitud, algoritmos fonéticos.

ABSTRACT

Often data that should be written so they are not identical due to misspellings and typos, variations in word order, use of prefixes and suffixes, among others. Phonetic techniques for duplicate detection are not geared toward the Spanish language, which makes the identification and correction of problems such as spelling errors in texts written in this language. In this paper we propose an algorithm called PhoneticSpanish to detect duplicate text strings which considers the presence of spelling errors in Spanish. The proposed algorithm was compared with nine techniques to detect duplicates. The results were satisfactory and the algorithm that performed better than the other techniques and demonstrate opportunities for improved analysis of information in Spanish.

KEY WORDS

Data cleansing, data quality, detection of duplicates, similarity functions, phonetic algorithms.

INTRODUCCIÓN

Actualmente las organizaciones acumulan grandes volúmenes de datos, que sirven de base para generar información y conocimiento. Los datos incorrectos pueden llevar a tomar decisiones equivocadas con la consiguiente pérdida de tiempo, dinero y credibilidad. Uno de los inconvenientes que se pueden presentar en los datos almacenados se da cuando una misma entidad del mundo real se almacena más de una vez de diferentes formas. El proceso para detectar este tipo de problemas se conoce como record linkage en el área de la estadística; database hardening en el área de la inteligencia artificial; merge-purge, data deduplication o instance identification en el área de las bases de datos; otros nombres como coreference resolution y duplicate record detection también se usan con frecuencia.

Este proceso fue identificado inicialmente por [1]. Algunos fundamentos probabilísticos fueron desarrollados posteriormente por [2], y formalizados por [3], como una regla de decisión probabilística. Algunas mejoras de este modelo han sido propuestas por [4]. Esencialmente, el proceso es como sigue: dado un conjunto R de registros: i) se define un umbral en el intervalo cerrado [0,1], ii) se compara cada registro con los demás registros y iii) si la similitud entre una pareja de registros es mayor o igual que el umbral, se supone que son duplicados y se considera que son representaciones de una misma entidad del mundo real.

Para ilustrar esta situación, supóngase que en un sistema de salud, cada vez que un paciente ingresa en un hospital se registran sus datos; de esta forma, su nombre se podría ingresar de diferentes formas debido a errores ortográficos o tipográficos, uso de abreviaturas o debido a palabras faltantes.

Se han desarrollado funciones de similitud para la detección de duplicados; algunas de ellas son de tipo fonético como Soundex [5], Metaphone [6] Double Metaphone [7] Onca [8] Nysiis [9]. Estas técnicas, se basan en la forma como se pronuncian las palabras en un idioma en particular y no están orientadas al idioma español. Otro tipo de funciones de similitud se basa en emparejamiento de patrones. En esta última categoría, se encuentran técnicas como Levenshtein, Brecha Afín, Smith-Waterman, Jaro, Jaro-Winkler, Bi-grams, Tri-grams, Monge-Elkan y SoftTF-IDF. En este artículo se propone un algoritmo que considera las particularidades del idioma español y compara sus resultados con los de estas técnicas.

Para la concepción del algoritmo, se caracterizaron las técnicas mencionadas, con el fin de evaluar sus fortalezas y debilidades en cuanto a la detección de errores ortográficos en el idioma español. El algoritmo se comparó contra las nueve técnicas de emparejamiento de patrones mediante varios conjuntos de datos de prueba. El resto del artículo está organizado así: en la sección 2 se describen las nueve funciones de similitud sobre cadenas de texto con las cuales se compara el algoritmo propuesto. En la sección 3 se describe el algoritmo propuesto PhoneticSpanish. En la sección 4 se describe la métrica usada para la evaluación de las funciones de similitud. En la sección 5 se describe el diseño de los experimentos realizados para evaluar la eficacia de las funciones. En la sección 6 se muestran los resultados obtenidos. Por último, en la sección 7 se presentan las conclusiones y posibles trabajos futuros.

1 FUNCIONES DE SIMILITUD SOBRE CADENAS DE TEXTO

Se considera la siguiente notación: Σ denota algún conjunto finito ordenado de caracteres y Σ* el conjunto de cadenas formadas por la concatenación de cero o más caracteres de Σ. A y B denotan dos cadenas de texto de longitud n y m definidas sobre Σ*, donde n ≥ m. a_i representa algún carácter de A para 1 ≤ i ≤ n y b_j es análogo respecto a B. Los términos distancia y similitud entre dos cadenas se relacionan así: una distancia d ε [0,1], d ε R donde 0 indica que ambas cadenas son idénticas y 1 que no tienen caracteres en común, equivale a una similitud s = 1 – d, lo que indica que a mayor distancia menor es la similitud y viceversa.

1.1 Funciones de similitud basadas en caracteres

Estas funciones consideran cada cadena de caracteres como una secuencia ininterrumpida de caracteres. En esta sección se consideraron cinco de las más conocidas.

Distancia de edición

La distancia de edición entre dos cadenas de texto A y B se basa en el conjunto mínimo de operaciones de edición necesarias para transformar A en B (o viceversa). Las operaciones de edición permitidas son eliminación, inserción y sustitución de un carácter.

En el modelo original [10] cada operación de edición tiene costo unitario. En [11] modificaron este modelo con operaciones de edición de distinto costo, lo que permite modelar errores ortográficos y tipográficos comunes. En los modelos anteriores la distancia entre dos cadenas carece de algún tipo de normalización, lo que se considera una gran desventaja. Por ejemplo, tres errores son más significativos entre dos cadenas de texto de longitud cuatro que entre dos cadenas de longitud veinte. Como consecuencia, se han propuesto varias técnicas de normalización. Las más simples normalizan dividiendo por la longitud de la cadena más larga [12] o por la suma de la longitud de ambas cadenas [13]. Más recientemente, en [14] desarrollaron una técnica de normalización que satisface la desigualdad triangular. Estas técnicas varían de O(nm) a O(n²m).

Distancia de brecha afín

La distancia de edición y otras funciones de similitud tienden a fallar cuando van a identificar cadenas equivalentes que han sido demasiado ''truncadas'', ya sea mediante el uso de abreviaturas o la omisión de tokens. La distancia de brecha afín ofrece una solución al penalizar la inserción/eliminación de k caracteres consecutivos (brecha) con bajo costo, mediante una función afín R(k) = g + h · (k–1), donde g es el costo de iniciar una brecha, h el costo de extenderla un carácter y h << g. En [15] se describe un modelo para entrenar automáticamente esta función de similitud a partir de un conjunto de datos.

Similitud Smith-Waterman

La similitud Smith-Waterman [16] entre dos cadenas A y B es la máxima similitud entre una pareja (A', B'), sobre todas las posibles, tal que A' es subcadena de A y B' es subcadena de B. El modelo original define las mismas operaciones de la distancia de edición y, además, permite omitir cualquier número de caracteres al principio o al final de ambas cadenas. Este aspecto permite identificar cadenas equivalentes con prefijos/sufijos que, al no tener valor semántico, pueden ser descartados. Es posible normalizar la similitud de [16] con base en la longitud de la cadena de mayor longitud, la de menor longitud o la longitud media de ambas cadenas [12] que corresponden a los coeficientes de Jaccar, Overlap y Dice. La similitud Smith-Waterman se puede calcular en O(nm) mediante el algoritmo propuesto en [16]. En 1992 [17] presentan un algoritmo de orden O(n) para verificar si la similitud Smith-Waterman entre dos cadenas es menor que cierta constante k.

Similitud de Jaro

Jaro desarrolló una función de similitud que define la trasposición de dos caracteres como la única operación de edición permitida. Los caracteres no necesitan ser adyacentes y pueden estar alejados cierta distancia d que depende de la longitud de ambas cadenas [18]. En 1993 [4] propone una variante que asigna puntajes de similitud mayores a cadenas que comparten algún prefijo, basándose en un estudio realizado por [19]. En [20] se propone un modelo basado en distribuciones gaussianas.

Similitud de q-grams

Un q-gram, también llamado n-gram, es una subcadena de longitud q [21]. El principio tras esta función de similitud es que, cuando dos cadenas son muy similares tienen muchos q-grams en común. Es común usar uni-grams (q = 1), bi-grams o di-grams (q = 2) y tri-grams (q = 3). Es posible agregar q – 1 ocurrencias de un carácter especial (no definido en el alfabeto Σ original) al principio y final de ambas cadenas. Esto llevará a un puntaje de similitud mayor entre cadenas que compartan algún prefijo o sufijo, aunque presenten diferencias en el medio. Por ejemplo, la cadena ''Peter'' contiene los bi-grams ''Pe'', ''et'', ''te'', ''er'' y los 1-skip-2-grams ''Pt'', ''ee'', ''tr''. La similitud de q-grams se puede calcular en O(n) [22]. En [23] se presenta un algoritmo alternativo para q-grams basado en autómatas de sufijos que también tiene un orden O(n).

1.2 Funciones de similitud basadas en tokens

Estas funciones consideran cada cadena como un conjunto de subcadenas separadas por caracteres especiales, espacios en blanco, puntos y comas, como un conjunto de tokens, y calculan la similitud entre cada pareja de tokens mediante alguna función de similitud basada en caracteres. En esta sección se consideran dos de las funciones basadas en tokens más conocidas.

Similitud de Monge-Elkan

Dadas dos cadenas A y B, sean α₁, α₂ ... a_K y β₁, β₂ ... b_L sus tokens respectivamente. Para cada token α_i existe algún β_i de máxima similitud. Entonces la similitud de Monge-Elkan entre A y B y es la similitud máxima promedio entre una pareja (a, β_i). El algoritmo para la similitud de Monge-Elkan tiene un orden computacional O(nm) [20].

Similitud coseno TF-IDF

Dadas dos cadenas A y B, sean α₁, α₂ ... a_K y β₁, β₂ ... b_L sus tokens respectivamente, que se pueden ver como dos vectores V_A y V_B y de K y L componentes. En [20] se propone una función que mide la similitud entre A y B como el coseno del ángulo que forman sus respectivos vectores.

2 ALGORITMO PROPUESTO

El algoritmo propuesto, usa un sistema de codificación similar al del algoritmo Soundex. Soundex es un algoritmo de codificación fonética, que convierte una palabra en un código [24]. El código Soundex consiste en sustituir las consonantes de la palabra afectada por un número; si es necesario se agregan ceros al final del código para conformar un código de 4 dígitos. Soundex elige la clasificación de los caracteres con base en el lugar de articulación de la lengua inglesa. La tabla 1 presenta las equivalencias usadas por Soundex

Debido a que en el idioma inglés, las letras A, E, I, O, U, H, W y Y no hacen diferenciación fonética, son descartadas. Adicionalmente existen otras reglas complementarias para la codificación de las letras dobles (si el texto tiene letras dobles, estas se deben tratar como una sola) y para letras a lado y lado con el mismo código (si el texto tiene diferentes letras lado a lado que tienen el mismo número en la guía de codificación Soundex, estas se deben tratar como una sola letra), entre otras.

Por ejemplo: Giraldo se codifica G643 (G, 6 por la R, 4 por la L, 3 por la D, las otras letras se descartan). Juan se codifica J500 (J, 5 por la N, las otras letras se descartan, y se agregan dos ceros).

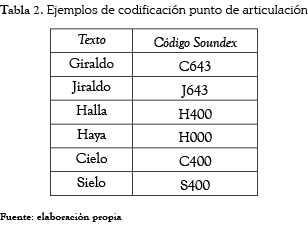
Las limitaciones del algoritmo Soundex han sido ampliamente documentadas [25, 26] y han dado lugar a varias mejoras, pero ninguna orientada hacia el idioma español. Es claro, que Soundex no está orientado al español ya que ni siquiera contempla el juego de caracteres (''ñ'', ''ll''). Asimismo, la dependencia de la letra inicial, la agrupación por punto de articulación del idioma inglés y el estar limitado a cuatro caracteres implica que no es eficiente para detectar errores ortográficos comunes en el idioma español. En la tabla 2 se presentan ejemplos de problemas ortográficos que se mantienen con esta codificación.

En [27] se realiza un estudio según el cual el 90% de los errores que se presentan en la escritura de la lengua española son errores simples (un solo error por palabra). Este estudio incluye las palabras homófonas, las cuales se presentan cuando el escritor hace una sustitución de un carácter que es fonéticamente correcto, pero ortográficamente incorrecto y se presentan por problemas cognitivos (errores en pares fonéticamente similares como, b-v, s-x, c-s, ll-y como en Jiraldo-Giraldo, estención-extensión, llendo-yendo). Este tipo de errores son comunes tanto en errores simples, como en errores múltiples (más de un error por palabra), y junto con el problema de las tildes y las mayúsculas alcanzan un 63% de los errores en el idioma español. A este porcentaje se dirige la nueva codificación propuesta en este artículo.

En [28] se aporta la información necesaria para construir el nuevo algoritmo. La tabla 3, tomada literalmente de dicho trabajo (se excluyen algunas columnas para reducir su tamaño), corresponde a la frecuencia con que una letra se usa en lugar de otra en el idioma español. X representa a la letra correcta e Y la incorrecta que es colocada por error en su lugar. Con excepción de las vocales, las frecuencias más altas (enmarcadas en rectángulos), pertenecen a las variaciones de las letras s-c-x-z, v-b, j-g, m-n-ñ.

La tabla 4 presenta la codificación para el algoritmo propuesto PhoneticSpanish, en la cual los grupos se arman con base en los problemas ortográficos frecuentes en el idioma español y contemplando caracteres de este idioma como la ''ñ'' y la ''ll''. La ''y'', fuente de múltiples errores ortográficos en español al confundirla con la ''ll'', no se descarta sino que incluye en el mismo grupo.

La tabla 5 presenta ejemplos usando este sistema de codificación. Puede observarse que el código arrojado es el mismo, a pesar de no ser textos idénticos debido a los errores ortográficos cometidos.

2.1 Algoritmo

Paso 1. Escribir todas las letras en mayúscula y descartar todos los signos de puntuación. Rellenar la palabra con espacios en blanco cuando sea necesario durante todos los pasos del procedimiento.

Paso 2. Eliminar las siguientes letras: 'A', E', 'I', 'O', 'U', 'H', 'W'

Paso 3. Cambiar las letras de los siguientes conjuntos por el dígito correspondiente: 0 = 'P', 1 = 'B', 'V', 2 = 'F', 'H', 3 = 'T', 'D', 4 = 'S', 'Z', 'C', 'X', 5 = 'Y', 'LL', 'L', 6= 'N', 'Ñ', 'M', 7= 'Q', 'K', 8= 'G', 'J', 9= 'R', 'RR'

3 EVALUACIÓN DE FUNCIONES DE SIMILITUD SOBRE CADENAS DE TEXTO

Las curvas de precisión y de memoria se usan para evaluar las funciones de similitud sobre cadenas de texto. Dichas curvas se obtienen a partir de un tipo especial de consultas conocidas como top-k queries, en las cuales se retornan las k instancias más similares a la cadena buscada. Para una función de similitud particular, su curva de precisión y de memoria mide la capacidad que tiene para ubicar las cadenas similares a la buscada dentro de los primeros k resultados [29]. En este contexto, una técnica de evaluación acertada debe considerar:

- Si la función de similitud consigue separar correctamente cadenas relevantes de irrelevantes, asignando puntajes superiores al umbral a las primeras e inferiores al umbral a las últimas.

- El grado de separación entre cadenas relevantes e irrelevantes. Una buena función de similitud no solo debe distinguir entre unas y otras, sino ubicarlas dentro de una distancia razonable de forma que queden clasificadas en dos conjuntos distintos.

- La variación del umbral t seleccionado, pues la distribución de valores de similitud puede variar de un conjunto de datos a otro.

Las curvas de precisión y de memoria solo consideran el primer aspecto. Por esta razón, en el presente trabajo se usa una métrica de evaluación propuesta por [30], llamada función de discernibilidad.

3.1 Función de discernibilidad

La discernibilidad es una métrica que ha sido usada en trabajos comparativos como es el caso de la herramienta SimEval [29] para determinar cuán eficaces son las funciones de similitud identificando las entradas que realmente corresponden a un mismo objeto. Esta métrica intrínsecamente incorpora los cuatro elementos tradicionales de una tabla de contingencia o matriz de confusión de 2*2: aciertos, desaciertos, falsos positivos y falsos negativos.

La discernibilidad de una función de similitud se calcula así [30]:

El rango determina el intervalo de umbrales que mejor separa las cadenas relevantes de las irrelevantes, ya que actúa como indicador de la distancia entre estas (así, entre mayor sea, mejor), y se puede calcular por cualquiera de los dos algoritmos propuestos en [30]. El término indica el porcentaje logrado de separaciones correctas. Los coeficientes c₁ y c₂ permiten controlar la importancia de cada uno de los dos aspectos anteriores. Independientemente de los valores dados a c₁ y c₂, los valores de discernibilidad siempre estarán en el intervalo [-1,1]: -1 en el peor caso, y 1 en el caso de la función de similitud ideal, que logra separar correctamente todas las cadenas relevantes de las irrelevantes a la distancia máxima posible.

4 DISEÑO DEL EXPERIMENTO PARA LA COMPARACIÓN DE LAS TÉCNICAS

Usando la función de discernibilidad, se compararon nueve funciones de similitud sobre cadenas bajo la situación problemática propuesta (errores ortográficos) contra el algoritmo propuesto. Para las pruebas realizadas se definió c₁ = 3 y c₂ = 7 en la ecuación (1), de forma que el intervalo óptimo contribuya en 30% al valor de discernibilidad y F_max / 2|Q| en 70%. Al dar igual importancia a ambos factores (c₁ = 1 y c₂ = 1), una función de similitud podría obtener un valor de discernibilidad considerablemente alto con un intervalo óptimo ancho de umbrales que logren un porcentaje de separaciones correctas bajo, lo cual no tiene sentido.

Mediante la herramienta Web Fake Name Generator se generaron aleatoriamente conjuntos de datos compuestos por registros con atributos como nombre, apellidos, dirección, ocupación y correo electrónico. A partir de estos, se derivaron otros con nuevas cadenas a las cuales se les introdujeron errores de ortografía cambiando unas letras por otras (g por j, v por b, c por s, y por ll, entre otras).

Se generaron diez conjuntos de datos de prueba con las respectivas variaciones ortográficas. Cada conjunto de datos con 400 cadenas de texto representando 200 entidades (dos cadenas por entidad). Se comparó la eficacia en la detección de los duplicados para las siguientes funciones de similitud: distancia de Levenshtein, distancia de brecha afín, similitud Smith-Waterman, similitud de Jaro y Jaro-Winkler, similitud de bi-grams y tri-grams, similitud de Monge-Elkan y similitud SoftTF-IDF contra el algoritmo propuesto.

5 RESULTADOS

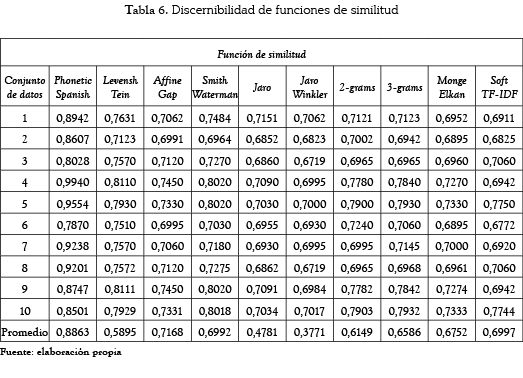
La tabla 6 muestra los resultados de la discernibilidad al aplicar las nueve funciones de similitud más el algoritmo propio (llamado PhoneticSpanish) sobre los diez conjuntos de datos. El promedio más alto (0,8863) de la discernibilidad lo obtuvo el algoritmo propuesto seguido por la función de brecha afín (0,7168).

Debido a que estos promedios no permiten llegar a conclusiones definitivas, se pretendió efectuar un análisis de varianza (ANOVA) con el fin de determinar si las diferencias encontradas con las distintas técnicas eran estadísticamente significativas, según el índice de discernibilidad, pero luego de realizar la prueba de Kolmogorov-Smirnov se determinó que el supuesto de normalidad no se cumple. Por ello, en su lugar se aplicó la prueba no paramétrica de Kruskal-Wallis, la cual no requiere que se cumplan los supuestos de normalidad y homoscedasticidad [31]. Esta prueba permite verificar la hipótesis nula de igualdad de las medianas del grado de discernibilidad para las diez funciones de similitud. La tabla 7 presenta los resultados.

La prueba de Kruskal-Wallis arrojó como resultado para todas las situaciones problemáticas un valor p inferior a 0,05; por ello se puede afirmar que hay diferencias estadísticamente significativas entre las medianas, con un nivel de confianza del 95%. La columna de la derecha corresponde al rango promedio y al ordenar por su valor se puede establecer que tan exitosas son las funciones de similitud en cuanto a la discernibilidad.

Asimismo, se construyó un Gráfico de Cajas y Bigotes, como ayuda para la visualización de las medianas significativamente diferentes, véase la figura 1.

Una vez comprobado que las diferencias existentes entre las técnicas son estadísticamente significativas, se puede concluir que el algoritmo propuesto, realizó un mejor trabajo que las otras nueve funciones de similitud con las que se comparó en cuanto a detección de cadenas de texto duplicadas con errores ortográficos para el idioma español sobre los datos de prueba.

6 CONCLUSIONES Y TRABAJOS FUTUROS

Existen diversas funciones de similitud sobre cadenas de texto pero no consideran las particularidades del idioma español, lo que las hace inapropiadas en tareas de detección de duplicados originadas por errores ortográficos en este idioma. En este trabajo se planteó una nueva técnica por medio de un algoritmo con principios fonéticos considerando las características propias de la lengua española.

La comparación con nueve técnicas convencionales para la detección de duplicados arrojó mejores resultados en cuanto a la discernibilidad, el algoritmo propuesto fue más eficaz al ser aplicado sobre el caso de prueba diseñado.

Como trabajo futuro se planea implementar en el algoritmo, técnicas de emparejamiento de patrones que permitan un mejor comportamiento en otras situaciones como abreviaturas, palabras en desorden, presencia de sufijos y prefijos, entre otras.

REFERENCIAS

[1] Dunn, H. L. 1946. Record Linkage, Americal Journal of Public Health, 36, 12, 1412-1416.        [ Links ]

[2] Newcombe, H. y Kennedy, J. 1962. Record Linkage: Making Maximum Use of the Discriminating Power of Identifying Information, Communications of the ACM, 5, 11, 563- 566.        [ Links ]

[3] Fellegi, I. P. y Sunter, A. B. 1969. A Theory for Record Linkage, Journal of the American Statistical Association, 64, 328, 1183-1210.        [ Links ]

[4] Winkler, W. E. 1993. Improved Decision Rules in the Felligi-Sunter Model of Record Linkage. En Proceedings of the Section on Survey Research Methods, 274-279.        [ Links ]

[5] Reghavan, H. y Allan, J. (2004). Using Soundex Codes for Indexing Names in ASR documents.        [ Links ]

[6] Philips, L. 1990. Hanging on the Metaphone, Computer Language Magazine, 7(12), 39-44, Diciembre, 1990.        [ Links ]

[7] Philips, L. 2000. The Double Metaphone Search Algorithm,'' C/C++ Users J., 18(5), Junio, 2000.        [ Links ]

[8] Gill, L. E. 1997. OX-LINK: The Oxford Medical Record Linkage System. En: Proceedings of International Record Linkage Workshop and Exposition, (Arlington, Estados Unidos, marzo 20-21, 15-33.        [ Links ]

[9] Taft, R. L. 1970. Name Search Techniques. Technical Report Special Report No. 1, Nueva York State Identification and Intelligence System, Albany, N. Y., febrero, 1970.        [ Links ]

[10] Levenshtein, V. I. 1966. Binary Codes Capable of Correcting Deletions, Insertions, and Reversals. Soviet Physics Doklady, 10, 8, 707-710.        [ Links ]

[11] Needleman, S.B. y Wunsh, C. D. 1970. A General Method Applicable to the Search for Similarities in the Amino Acid Sequence of Two Proteins, J Mol Biol, 48, 3, 443–453.        [ Links ]

[12] Christen, P. 2006. A Comparison of Personal Name Matching: Techniques and Practical Issues. En Sixth IEEE International Conference on Data Mining, 290-294.        [ Links ]

[13] Weigel, A. y Fein, F. 1994. Normalizing the Weighted Edit Distance. Proceedings of the 12th IAPR International Conference on Pattern Recognition, 399-402.        [ Links ]

[14] Yujian, L. y Bo, L. 2007. A Normalized Levenshtein Distance Metric, IEEE Transactions on Pattern Analysis and Machine Intelligence, 29, 6, 1091-1095.        [ Links ]

[15] Gotoh, O. 1982. An Improved Algorithm for Matching Biological Sequences, Journal of Molecular Biology, 162, 3, 705-708.        [ Links ]

[16] Smith, T. F. y Waterman, M. S. 1981. Identification of Common Molecular Subsequences, Journal of Molecular Biology, 147, 1, 195-197.        [ Links ]

[17] Baeza-Yates, R., y Gonnet, G. H. 1992. A new approach to Text Searching. Communications of the ACM. 35, 10, 74-82.        [ Links ]

[18] Jaro, M. A. 1976. Unimatch: A Record Linkage System User's Manual, technical report, Washington, D. C.: US Bureau of the Census.        [ Links ]

[19] Pollock, J. J. y Zamora, A. 1984. Automatic Spelling Correction in Scientific and Scholarly Text, Communications of the ACM, 27, 4, 358-368.        [ Links ]

[20] Cohen, W. W., Ravikumarand, P. Fienberg, S. E. 2003. A Comparison of String Distance Metrics for Name-Matching Tasks. En International Joint Conference on Artificial Intelligence, 73-78.        [ Links ]

[21] Yancey, W. E. 2006. Evaluating String Comparator Performance for Record Linkage. En Proceedings of the Fifth Australasian Conference on Data mining and Analytics, 23-21.        [ Links ]

[22] Ukkonen, E. 1992. Aproximate String-Matching With Q-grams and Maximal Matches, Theoretical Computer Science, 92, 1, 191-211.        [ Links ]

[23] Cohen, J. D. 1997. Recursive Hashing Functions for n-Grams, ACM Transactions on Information Systems. 15, 3, 291-320.        [ Links ]

[24] Else, Willis I. 2002. The Complete Soundex Guide: Discovering the rules Used by the Census Bureau and the Inmigration and Naturalization Service When These organization Indexed Federal Records. Apollo, PA: Closon Press.        [ Links ]

[25] Stanier, Alan. 1990. How accurate is Soundex matching. CIG Vol. 3, n.° 7, 286-288.        [ Links ]

[26] Patman, F., and Shaefer, L. 2003 Is Soundex Good Enough for You? On the Hidden Risks of Soundex-Based Name Searching © 2001-2003 Language Analysis Systems, Inc        [ Links ]

[27] Ramírez, F., Arnaiz, A., Ginés, M. 2005. A Spell Checker for a World Language: The New Microsoft's Spanish Spell Checker.        [ Links ]

[28] Ramírez, F, López, E. 2006. Spelling Error Patterns in Spanish for Word Processing Applications.        [ Links ]

[29] Heusser, C. A., Krieser, F. N. y Orengo, V.M. 2007. SimEval-A Tool for Evaluating the Quality of Similarity Functions. En Tutorials, posters, panels and industrial contributions at the 26th International Conference on Conceptual Modeling, 71-76.        [ Links ]

[30] Da Silva, R., Stasiu, R., Orengo, V. M. y Heuser, C. A. 2007. Measuring Quality of Similarity Functions in Approximate Data Matching, Journal of Informetrics. 1, 1, 35-46.        [ Links ]

[31] Álvarez R. 2007. Estadística aplicada a las ciencias de la salud. Ed. Díaz de Santos. 1030p.        [ Links ]