INTRODUCCIÓN

Una red de sensores inalámbricos (WSN, por sus siglas en inglés) es un conjunto de dispositivos semejantes a un microcomputador distribuidos espacialmente en un área de interés, conocidos como nodos sensores; estos poseen unidad de memoria, pro cesamiento, radiofrecuencia y sensado, y una fuente de energía limitada. Los nodos sensores capturan, a través de su módulo de sensado, un conjunto de valores para cada parámetro de interés en el ambiente circundante, cuyos valores son enviados por el medio inalámbrico, en forma de paquetes de datos, hacia una estación base centrali zada que no tiene limitaciones de energía ¹⁾⁽². Entre las aplicaciones de despliegue de las WSN se destacan las construcciones civiles, ambientes de hogar, de salud, y los campos de cultivo. Este último contexto se conoce como agricultura de precisión.

La agricultura de precisión es un concepto de gestión de parcelas agrícolas que estudia la variabilidad de suelo y clima entre diferentes campos de cultivo con el fin de ajustar a la medida la aplicación de insumos como agua, fertilizantes, pesticidas, etc., y, consecuentemente, incrementar los niveles de productividad ³.

Una WSN usada en agricultura de precisión monitoriza la evolución del producto desde la siembra hasta la cosecha, lo cual implica un requerimiento en la longevidad de la red de por lo menos seis meses, que corresponde a dicho período ⁴.

La longevidad de una red de sensores se define como el período de tiempo que transcurre desde el inicio de operación de la red hasta que un nodo (o un porcentaje de ellos) es incapaz de enviar sus datos a la estación base porque se ha descargado su batería ¹.

Así, incrementar el ciclo de vida de una WSN se convierte en un reto de diseño porque: (i) los campos de cultivo en países en vía de desarrollo generalmente están ubicados en lugares montañosos y remotos, dificultando así recargar las baterías de los nodos sensores, (ii) la extensión de las parcelas está en términos de hectáreas, lo que significa que los paquetes de datos deben realizar recorridos extensos por la red hasta llegar a su destino: la estación base, y (iii) en una WSN la fase de transmisión de datos produce el mayor consumo energético debido al uso del módulo de radiofrecuencia; este consumo, a su vez, se ve afectado por la distancia del enlace de transmisión, entre otros parámetros.

En este sentido, Bari y sus colegas afirman ⁵: “el tiempo de vida de una WSN puede variar considerablemente dependiendo del esquema de enrutamiento usado”, mientras que en ⁶ se plantea: “la función de un protocolo de enrutamiento en una WSN es generar las vías para comunicar los dispositivos que se encuentran distribui dos en la red”.

En una etapa preliminar de esta propuesta, documentada en ⁷, se listaron los parámetros de influencia en la fase de transmisión de datos en una WSN aplicada a la agricultura de precisión, y se definió la función de aptitud para solucionar el enruta miento a través de un algoritmo genético simple.

En el presente artículo se propone MOR4WSN (Multi-Objective Routingfor Wireless Sensor Networks), una aproximación de optimización multi-objetivo para seleccionar las rutas de transmisión de los datos recolectados desde los nodos fuente hasta la estación base en una WSN desplegada en un ambiente agrícola, de tal manera que dichas rutas presenten ventajas para la longevidad de la red.

MOR4WSN adapta el NSGA-II para generar estructuras de enrutamiento de WSN con topología jerárquica. Las pruebas de simulación permiten comparar los efectos sobre el ciclo de vida de una WSN al utilizar MOR4WSN como su técnica de enrutamiento, frente a una técnica tradicional como lo es Tree Routing de Zig Bee.

El resto de este artículo se organiza de la siguiente manera: la sección 1 presenta el estado del arte con un marco teórico y los trabajos relacionados, la sección 2 describe la adaptación algorítmica propuesta, la sección 3 muestra resultados de la experimen tación, la sección 4 presenta las conclusiones y, finalmente, la sección 5 agradece a los entes financiadores de esta investigación.

1. ESTADO DEL ARTE

A. Definiciones previas

1) Algoritmo genético. El algoritmo genético inicia con un conjunto de posibles so luciones generadas aleatoriamente (población inicial) denominadas cromosomas (o individuos) que constan de un arreglo de genes siempre con igual longitud (ver Figura 1).

Figura 1 Cromosoma de 6 genes 

El algoritmo genético dispone de una función de aptitud que asigna una valoración a cada individuo, basado en qué tan cerca está de la solución óptima. La selección per mite crear descendencia a partir del proceso de cruza, mientras que los hijos creados experimentan la mutación; esto implica alterar genéticamente la generación actual con el fin de mejorarla respecto a los criterios que se están optimizando ⁸.

2) Algoritmo genético multi-objetivo. Las aproximaciones multi-objetivo buscan solución a un problema que involucra la optimización de varios objetivos en paralelo y normalmente contrapuestos. Un algoritmo genético multi-objetivo (MOGA, por sus siglas en inglés) modifica la forma como se calcula la aptitud de los individuos respecto al genético simple, siendo necesario definir un conjunto de funciones objetivo.

Por su naturaleza multi-objetivo, un MOGA no busca una única mejor solución, sino que produce un conjunto de soluciones, conocido como el conjunto de Pareto (o conjunto no dominado), refiriéndose a aquellas mejores soluciones de compromiso considerando todos los objetivos en juego.

Ejemplos de MOGA son: algoritmo genético de vector evaluado (VEGA, por sus siglas en inglés), algoritmo genético de nichos de Pareto (NPGA, por sus siglas en inglés) y algoritmo genético de clasificación no dominada (NSGA, por sus siglas en inglés). Estos algoritmos tienen complejidad computacional de ^{_{0 (mN3)}} , donde m es el número de objetivos y N es el tamaño de la población.

3) NSGA-II. Una evolución del NSGA es el NSGA-II (Fast Elitist Non Dominated Sorting Genetic Algorithm) propuesto por Kalyanmoy Deb en 2002 ⁹. El NSGA-II se ocupa de mantener diversidad entre las soluciones de la población, gracias a la incorporación de los parámetros sharingy crowding distance, logrando reducir su complejidad a ^_0(mN2) . Una explicación detallada del funcionamiento del NSGA-II se puede consultar en ¹⁰.

B. Trabajos relacionados

Para la generación de la población inicial existe la condición de que los genes (nodos) consecutivos no pueden exceder una distancia umbral ¹¹, mientras que la selección de un nodo de próximo salto depende de la distancia del enlace, del consumo de energía promedio del camino, y de la distancia del nodo actual hasta la estación base. Para la mutación se comparte información global de la población, gracias a la existencia de un registro histórico del mejor cromosoma (aquel con máximo valor de aptitud hasta el momento). En ¹² la función de aptitud la determina la energía residual de cada individuo y su carga de transmisión y recepción; se entiende por carga la energía requerida para recibir los paquetes entrantes de sus hijos y transmitirlos a su padre.

Por su parte, Bari y sus colegas ⁵ definen la función de aptitud de acuerdo con el tiempo de vida de la red en términos de rondas. Para la operación de mutación seleccionan, de entre los nodos relé, un nodo crítico que disipa la máxima energía, y se reemplaza el nodo de próximo salto de este nodo crítico por un nuevo nodo relé de próximo salto, o se desvía algún flujo de entrada de ese nodo crítico, hacia otro nodo relé.

En GAR ¹³, la función de aptitud se construye de manera que la distancia total cubierta por los nodos es minimizada en cada ronda. Para la mutación, de manera similar a (14), se selecciona un nodo crítico que en este caso es el gen que contribuye con la máxima distancia en una ronda, y lo reemplazan por otro nodo que conduzca a la estación base cubriendo una menor distancia.

De las anteriores aproximaciones, ninguna ha orientado la solución hacia un área de aplicación específica; esto permite que los parámetros incluidos en la función de aptitud se elijan de manera indiscriminada. Además, todas las propuestas trabajan con el algoritmo genético estándar cuya función de aptitud no tiene en cuenta la contradic ción que puede existir al optimizar varios parámetros simultáneamente.

MOR4WSN adapta el NSGA-II de manera que las funciones objetivo correspon den con variables extraídas de las características de las WSN desplegadas en campos de cultivo.

2. MOR4WSN

Esta sección presenta cada componente del NSGA-II que debe ser adaptado para con vertirse en MOR4WSN; se presentan sus dificultades de implementación y propuesta de solución.

A. Modelo de red

En los proyectos documentados en ^16)-(20 se ejecutaron despliegues de WSN en campos de cultivo con diferentes productos agrícolas. Del análisis de estos trabajos se define el modelo de red para MOR4WSN como sigue.

B. Representación de la solución

En MOR4WSN la representación del cromosoma se define como en los trabajos pre vios (11-15); el cromosoma representa un árbol de enrutamiento donde cada nodo está etiquetado con un número entero de 0 a N, siendo N la cantidad de nodos, como se observa en la figura 2a. En la Figura 2b el valor del gen en la posición 0 es 2, indican do que el nodo 0 selecciona al nodo 2 para transmitirle sus datos; el nodo 2 transmite hacia el nodo 5, y el valor en 5 es 6, indicando que el próximo nodo es la estación base. Por lo tanto la ruta completa de recolección de los datos del nodo 0 se expresa como el camino 0 → 2 → 5 → 6.

Figura 2 Solución de enrutamiento de una WSN 

C. Funciones objetivo

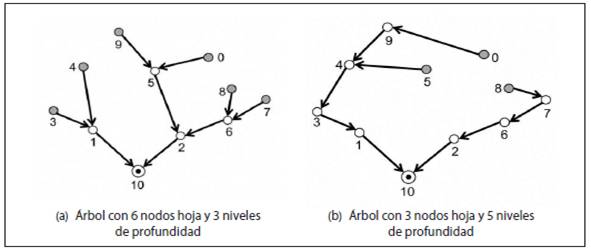
Cuando en una red jerárquica como la de la Figura 2a existen nodos que reciben y retransmiten paquetes de datos de muchos otros nodos de la red (nodos enrutadores), desgastarán sus baterías más rápidamente que aquellos nodos que realizan pocas retransmisiones; es por esto que, de acuerdo con los resultados en ²¹, una red de monitorización con estructura de árbol es longeva en la medida que se disminuya su cantidad de nodos hoja y su profundidad. Lo anterior se puede sintetizar como la búsqueda de balanceo de carga en la red, que se entiende como equilibrar el consumo de energía entre todos los nodos de la red; esto es, hacer una distribución equitativa de paquetes de datos recibidos, procesados y enviados ².

La Figura 3 indica que reducir simultáneamente el valor de los parámetros nodos hoja y profundidad en un árbol de enrutamiento es una situación contradictoria. De este modo, un MOGA es una metaheurística adecuada para el problema de enrutamiento.

Figura 3 Árboles de enrutamiento en una WSN 

Por otro lado, es pertinente tener en cuenta el consumo energético de cada estruc tura durante una ronda de sensado. La energía de transmisión y recepción consumida por cada nodo en una ronda de recolección de datos se modela con las ecuaciones (a) y (b) donde k es el tamaño del paquete y d la distancia de transmisión; E _elec es el co eficiente de energía eléctrica con la cual opera el radio, E _amp el coeficiente de energía del amplificador y n es el coeficiente de pérdida de camino que generalmente toma valores entre 2 y 4.

()a

()b

Finalmente, las funciones objetivo en MOR4WSN son:

Función objetivo 1: Disminuir la cantidad de nodos hoja.

Función objetivo 2: Disminuir la profundidad del árbol.

Función objetivo 3: Disminuir la energía consumida en cada ronda de sensado.

D. Población inicial

En la implementación genérica del NSGA-II los cromosomas de la población inicial se forman aleatoriamente de manera que los alelos de cada individuo toman cualquiervalor entre 0 y N (N es la cantidad de nodos de la red), permitiendo a un índice tomar un valor de alelo que no necesariamente está en su lista de vecinos, es decir, un nodo de próximo salto con el cual no se tenga comunicación directa. Dicho individuo sería inválido dentro de la población de MOR4WSN; por lo tanto, se debe asegurar que todos los cromosomas de la población inicial representen cromosomas válidos para el problema de enrutamiento. Se identifican entonces los siguientes puntos por resolver:

En MOR4WSN cada gen se forma entonces de la siguiente manera: los números mínimo y máximo que requiere el NSGA-II para sortear el valor de un alelo se toman del rango entre 0 y la cantidad de vecinos del nodo fuente (índice).

E. Cruza

En la Figura 4 es claro que el cruce de dos puntos puede generar hijos (topologías de enrutamiento) que no son árboles. En MOR4WSN es indispensable que todas las so luciones potenciales (cromosomas) sean árboles válidos para el enrutamiento.

Fuente: elaboración propia

Figura 4 Cruza de dos puntos que genera un hijo con ciclo 

Los puntos por resolver para MOR4WSN cada vez que se aplica el operador de cruza son:

F. Mutación

La Figura 5 indica que la aplicación de la mutación con el NSGA-II puede dar lugar a un ciclo en la estructura resultante, o a la no existencia de la estación base. Además, para lograr una topología funcional después de la mutación de un individuo, es indis pensable que el nuevo alelo sea vecino del índice alterado.

Figura 5 Mutación en NSGA-II 

MOR4WSN preserva árboles en las generaciones alteradas por la mutación, a través del diseño algorítmico que resuelve los siguientes aspectos:

G. Índice binario para seleccionar en el conjunto de Pareto

Siendo una aproximación evolutiva multi-objetivo, MOR4WSN no brinda una única solución (una única topología de árbol de enrutamiento), sino un conjunto de soluciones conocida como el conjunto de Pareto, el cual tiene el mismo tamaño que la población.

El concepto de dominancia de Pareto se ilustra en la Figura 6; aquí una solución a ‘domina’ a b siempre y cuando: a no sea peor que b en todos los objetivos, y asea estrictamente mejor que b en por lo menos un objetivo. Así, el conjunto de soluciones que no están dominadas por ninguna otra conforman el Frente no dominado también conocido como soluciones no dominadas de Pareto. En la Figura 6 estas soluciones no dominadas están representadas por los puntos 3 y 5.

Fuente: ¹⁰

Figura 6 Dominancia de Pareto 

En MOR4WSN el tamaño de la población toma valores del orden de los 100 individuos (N=100, 200,…), es decir, que la población optimizada respecto a las fun ciones objetivo brinda N soluciones entre las cuales un tomador de decisiones (cono cedor del contexto) debe seleccionar una única topología de enrutamiento, es decir, un único árbol optimizado. Para seleccionarlo es necesaria la existencia de preferencias, las cuales usualmente no están disponibles, es decir, no existen criterios para definir si una solución del conjunto de Pareto es preferible a otra, o el conjunto de datos es inmanejable para el tomador de decisiones.

Para seleccionar una solución multicriterio a posteriori en el conjunto de Pare to, algunos métodos (métodos outranking) llevan a cabo comparaciones por pares con el fin de establecer si existe preferencia, indiferencia o son incomparables. Sin embargo, estos métodos requieren que el tomador de decisiones establezca algunas ponderaciones ²².

En MOR4WSN un criterio para seleccionar solo una solución es evitar solucio nes atípicas que a menudo están presentes en el conjunto de Pareto porque no están dominadas por ninguna otra solución en uno de los objetivos. De esta manera, las soluciones del conjunto de Pareto se comparan por pares a través de un índice binario que representa cada árbol de enrutamiento; usando este índice las soluciones atípicas quedan excluidas de ser seleccionadas como estructura de enrutamiento final.

En el proceso comparativo cada árbol del frente de Pareto se compara con una estructura atípica, y MOR4WSN selecciona el árbol que tiene menor similitud con dicha estructura, como se ilustra en la Figura 7.

Figura 7 Comparador de grafos en MOR4WSN 

El comparador de la figura 7 hace lo siguiente: Sean G1 y G2 los grafos etique tados (que representan árboles de enrutamiento) que se compararán, siempre será G1 la solución atípica mientras que G2 es una solución no dominada no atípica como en la Figura 8a. Así, en la Figura 8b están los cromosomas correspondientes: G1 → C1 y G2 →C2.

Figura 8 Proceso de comparación de grafos 

Partiendo de C1 y C2 se crea la matriz S de tamaño N x 3 como se muestra en la Figura 8. S se crea de la siguiente manera:

La columna ^_Si3 subrayada en rojo en la figura 8c es un vector binario formado de las coincidencias de elementos en cada fila de S. Sea i la fila en consideración, si los elementos (i, 0) e (i, 1) de S coinciden exactamente, el elemento en la posición i de Si3 toma el valor de 1, de otra forma será 0. La matriz S es el índice de MOR4WSN; cada grafo tiene asociado su propio índice toda vez que S ordena la información necesaria para definir la similitud entre los grafos G1 y G2. Luego, con los elementos de la co lumna j=3 del índice de cada grafo se establece una relación de similitud como sigue:

Para el ejemplo de la figura 8 se tiene: N= 6, t = {0, 0, 0, 0, 1, 1}, z = 2, p = 33.33 %.

Lo anterior significa que el nivel de similitud entre G1 y G2 es del 33.33 %, valor que toma MOR4WSN como criterio de selección entre los elementos del conjunto de Pareto. A manera de tomador de decisiones el módulo del índice binario de MOR4WSN selecciona finalmente solo un árbol: aquel que tenga el menor valor de p entre los (N- 2)*2 valores de p calculados.

9. EVALUACIÓN

Las pruebas realizadas sobre esta versión de MOR4WSN permitieron determinar la duración del ciclo de vida alcanzado por una red usando enrutamiento con MOR4WSN y con TreeRouting² (TR). El ciclo de vida se mide en términos de las rondas de sensado alcanzadas en dos casos: (i) hasta que el primer nodo es incapaz de enviar sus datos a la estación base (el nodo muere), (ii) hasta que el 10 % de los nodos mueren.

Los resultados se muestran en la Figura 9; y permiten afirmar que, independien temente a la cantidad de nodos de la red, una aproximación multi-objetivo como MOR4WSN da lugar a una mayor cantidad de rondas de sensado que cuando se usa un enrutamiento mono-objetivo como TreeRouting.

Figura 9 Tiempo de vida de la WSN 

Cuando toma como referencia de longevidad la muerte del 10 % de los nodos de la red, MOR4WSN supera en el 95 % de los casos (diferentes cantidades de nodos) el ciclo de vida alcanzado respecto al uso de TreeRouting, como lo indica la Figura 8b.

10. CONCLUSIONES

En este artículo se modelan los elementos de las WSN en los algoritmos genéticos, y se definen los problemas de implementación que surgen con cada operador/componente del NSGA-II durante la adaptación para representar árboles de enrutamiento válidos.

La optimización del consumo de energía es fundamental para la implantación de redes de sensores inalámbricos en contextos como la agricultura de precisión; esta optimización de energía a través de un enfoque evolutivo multi-objetivo se reflejó en un aumento de longevidad como lo indican las gráficas de la Figura 8. En el momento se están realizando repetidas ejecuciones de las pruebas para determinar si hay alguna razón funcional para los picos presentados en las curvas de las figuras 8a y 8b cuan do la red tiene alrededor de 400, 700 y 900 nodos, o si se debe a algún ajuste en los parámetros de simulación.

11. AGRADECIMIENTOS

Los autores expresan agradecimiento a la Universidad del Cauca, a Colciencias y al proyecto AgroCloud de la Red Interinstitucional de Cambio Climático y Seguridad Alimentaria de Colombia (RICCLISA) por soportar esta investigación.