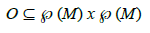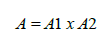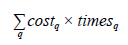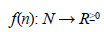English (pdf)
Article in xml format
Article references
Automatic translation
Send this article by e-mail
Cited by SciELO 
Cited by Google 
Similars in
SciELO 
Similars in Google 
Permalink
INTRODUCTION
Colombian standard NSR10 for earthquake-resistant buildings (Reglamento Colombiano de Construcciones Sismo Resistentes in its Spanish original) in its sections J and K describes the minimum safety requirements in the event of fire or any other event that threatens the safety of people inside buildings [1][2]. These requirements include (i) reducing fire risks or any other threat as much as possible; (ii) preventing fire hazards from reaching nearby buildings; (iii) facilitating people-evacuation tasks; (iv) facilitating mitigation of hazards; and (v) minimizing the risk of building collapse when evacuating people and extinguishing the threat [1]. Similarly, the Colombian government has adopted a National Policy for the Management of Disaster Risks (SNGRD) [3]; moreover, it has set out the guidelines for the construction of disaster risk management plans in public and private organizations (see Decree 2157 of 2017) [4]. These guidelines lay out the actions for effecting evacuation plans so that people inside a building (e.g., house, office, school, mall, etc.) can exit from it orderly, rapidly, and safely so that their lives are protected. Such actions concern (i) the identification of the building and its surroundings; (ii) protective measures for evacuations; (iii) evacuation paths; (iv) evacuation signage and warnings; and (v) identification of permanent and temporary safety points [5][6].
Although all these elements are important in the elaboration of an evacuation plan, the ultimate purpose of such a plan is to guarantee the rapid and safe movement of people away from any threat (e.g., fire) or accident (e.g., explosion) in the shortest possible time [7]. However, an evacuation plan may involve the evaluation of an exceedingly large number of evacuation routes in particular scenarios (e.g., buildings, city, etc.), which can be quite complex in view of the combinatorial nature of the problem [8-12]. Currently, research on evacuation routes comprises the following six categories [13]: level of service, mathematical models, heuristic methods, stochastic models, simulation tools, and multiagent systems. However, few works analyze the mathematical complexity of these techniques [14], a fundamental aspect when selecting one option over another. Specifically, in relation to the time and space used by the algorithms to solve the problem according to the size or length of the input [15]. Moreover, when these technologies, at most, generate a single solution to the problem of evacuation routes [16-18]. For this reason, this work analyzes the complexity, in terms of execution time, of algorithm BEPtoPNST [19-24] with the aim to advance in the development of computational strategies that allow efficient planning of evacuation routes. The novel algorithm BEPtoPNST allows not only to generate the optimal evacuation plan, but also sub-optimal plans [19-24], which uses a graph-theoretical approach based on P-graphs (process graphs) [25-31]. In what follows, the methods used are described, algorithm BEPtoPNST is analyzed asymptotically, and finally, conclusions are drawn.
1. METHODS
1.1 Problem Definition
A building-evacuation problem (BEP) can be modeled as a directed graph [8]; the goal is to minimize the evacuation time. Let G = (N, A) be a directed graph with N the set of nodes and A the set of arcs; each node n N represents potential locations of evacuees and other areas on the building (e.g., rooms or stairs). Moreover, the possible movements between locations through k (e.g., corridors or doors) are represented by arcs (i, j, k)A, such that i, j A (see figure 1); furthermore, G must satisfy the restrictions of the building [8]. Specifically, each location n has a limited capacity expressed by a non-negative integer, capn, representing the number of people that can be accommodated in n.
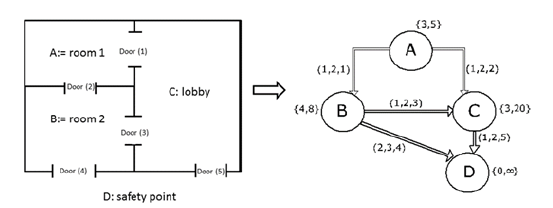
Source: taken from REF _Ref50116325 \r \h \* MERGEFORMAT [20].
Figure 1 Conventional adopted graph-based notation for representing building-floor maps REF_Ref420414599 \r \h \* MERGEFORMAT [8]: {initial contents, node capacity}; (travel time, arc capacity, arc id)
For each location, a non-negative integer is assigned to initial occupancy, ic n , signifying the number of people at any location in the event of an emergency. In addition, a positive integer, cap (i,j,k) , is assigned to the maximum flow rate of corridor (i,j,k), which represents the maximum number of people that can pass through a corridor simultaneously. Finally, each corridor (i,j,k) is constrained by travel time λ (i,j,k) , a non-negative integer that measures the time a person takes to traverse the total length of a passageway [8-12].
1.2 Process Graphs (P-graphs)
An innovative approach called P-graph has been proposed to facilitate the solution of process-network synthesis (PNS) problems [27]. A P-graph is a mathematically rigorous bipartite graph that allows the graphical representation of a PNS problem [32][33]. The P-graphs together with a solid axiomatic basis facilitate the construction of structures (flowsheets) of a given process by algorithmically combining operating units that are part of the process. A P-graph is formally defined in equation (1) in terms of a set of operating units, O, as a subset of the cartesian product of all subsets of materials, M, as
(1)
where ℘ (M) denotes the power set of M and x, the cartesian product. Moreover, in equation (2), a P-graph is defined as a pair (M, O) whose vertices are elements of set V given by
(2)
Vertices M-type and O-type belong to the M and O sets, respectively. The arcs of the graph are the elements described by the following expressions in equations (3), (4), and (5).
(3)
where
(4)
and
(5)
Thus, X indicates an M-type vertex; Y, an O-type vertex; α, a set of M-type vertices, of which the arcs are directed to the O-type vertices; and β, a set of M-type vertices whose arcs are directed to the O-type vertices [26]. For illustration, let M be a set of materials, M = {A,B,C,D,E,F}, and O a set of operating units given by O = {({B,A}, {A}), ({D,E}, {B,C}), ({F},{A,C}), ({F}, {A,C})}. It can be verified that M and O satisfy the restrictions (1-5), such that (M,O) is a P-graph as shown in figure 2 [27].
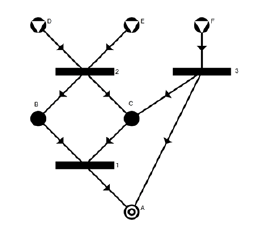
Source: adapted from REF _Ref36019017 \r \h \* MERGEFORMAT [27].
Figure 2 P-graph (M,O) where A,B,C,D,E, and F are materials, and 1,2, and 3 are the operating units: represents raw materials or input elements of the whole process; symbolizes intermediate-materials or elements, emerging between the operating units; and represents products or outputs of the entire process
1.3 Analysis of Algorithms
Algorithm analysis plays a critical role in computer science as it guides the assessment of efficient procedures for addressing any given computational problem [34] [35]. This assessment is based on the execution time of the instructions, or steps, that an algorithm must follow without considering the impact of other factors [35].
Equation (6) embodies the mathematical model used to analyze the complexity of algorithm BEPtoPNS T . At the outset, the basic instructions (q) of the algorithm are identified; then, their costs are determined (cost q ), and finally, the number of times that those operations are executed (times q ) is analyzed [36].
(6)
Most algorithms work well with small inputs; however, we are interested in analyzing the behavior of the algorithm when the input size is large enough. To this end, we define the execution time of an algorithm as in equation (7).
(7)
where n∈N represents the size of the input, f(n), the number of steps executed by the algorithm given n, and R≥0), the set of non-negative real numbers. Therefore, attention is given to the behavior of f(n) when n increases. The above expression allows to relate the asymptotic behavior of an algorithm through f(n). Based on f(n), functions O(f(n)), Ω(f(n)), and Θ(f(n)) are defined [15],[35-38], thus signifying, respectively, a function that provides an upper limit (worst case, maximum number of instructions performed by an algorithm), one that provides a lower limit (best case, minimum number of instructions performed by an algorithm), and a function that is contained between the upper and lower limits, in the order of growth of the function. The ideal is to analyze the asymptotic behavior in the worst case of any given algorithm [15],[35-38]; therefore, it is important to define the term, O. The notation O, O(f(n)) defines the set of all functions g(n)∶ N →R≥0, such that for some natural number n 0 and some positive real number c, g(n) ≤ c f (n), as long asn ≥ n 0 [35]. Informally, we say that the expression g(n) is less than or equal to some constant multiple of f(n).
2. ALGORITHM BEPTOPNS T
Algorithm BEPtoPNST transforms a BEP into a PNS T problem, thus representing the temporal dimension of a BEP (i.e., evacuation time), which is solved with the aid of the P-graph method [25-31]. The algorithm consists of two parts: initialization and time expansion. During initialization, the materials that describe a PNS problem are identified. Such materials are determined from the nodes specified in the graph that describes the floor map of a building. These materials can be (i) raw materials, (ii) intermediate materials, and (iii) products. The raw materials represent locations in the building where people are located just before the emergency alarm is activated; intermediate materials represent empty locations; and the products represent safety points, or meeting areas, outside of it. On the other hand, the time expansion identifies the operational units of a PNS problem, which describe the way in which people move during an evacuation plan. Such movements can be of two types: (i) from one location to another; or (ii) a momentary pause at the current location. A more detailed discussion on algorithm BEPtoPNS T is presented elsewhere [20]. Table 1 lists the elements involved in the specification of algorithm BEPtoPNS T , as well as the analysis of its complexity.
Table 1 Mathematical notation for specifying algorithm BEPtoPNS T .
| Symbol | Description |
|---|---|
| R | set of raw materials, that is, the locations with people at the beginning of the evacuation in the original problem |
| r | element of R, i.e., r ∈ R |
| U r | upper limit of r, that is, the number of people at location r at the start of the evacuation |
| L r | lower limit of r, that is, 0 |
| | | | cardinality of a set, that is, the number of elements contained in it |
| P | set of products, that is, the exits or safe points outside the building once the evacuation of the building has begun |
|
the total number of people inside the building at the start of the evacuation |
| T | maximum time expected to evacuate the building |
| t | unit of time |
| M i_(t+1) | number of individuals accommodated in i at t + 1 |
| O i_i_t_(t+1) | number of individuals who prefer to be in a specific location, i, at least one more unit of time, i.e., t + 1. |
| L O _ i_i_t_(t+1) | lower limit of O i_i_t_(t+1) , that is, the number of people that can be at location i at least one more time unit, i.e., t + 1 |
| U O_i_i_t_(t+1) | upper limit of O i_i_t_(t+1) , that is, the number of people that can be at location i at least one more unit of time, i.e., t + 1, that is cap i |
| O i_j_t_(t+λ_ijk)_k | number of individuals walking from location i at time t to location j through a corridor k at time (i,j,k) + t |
| L O_i_j_t_(t+λ_ijk)_k | lower limit of O i_j_t_(t+λ_ijk)_k , that is, the number of individuals that walk from location i at time t to location j through a corridor k at time (i,j,k) + t |
| U Oi_j_t_(t+λ_ijk)_k | upper limit of O i_j_t_(t+λ_ijk)_k , that is, the number of individuals who walk from location i at time t to location j through a corridor k at time (i,j,k) + t |
| O evactime_t | people who reach a safety point, k, at time t |
| L Oevactime_t | lower limit of people who will reach a safety point, k, at time t |
| U Oevactime_t | upper limit of people who reach a safety point, k, at time t |
| cp Oevactime_t | proportional cost associated with the number of people who reach a safety point, k, at time t |
Source: own elaboration
2.1 Complexity Analysis
As mentioned earlier, algorithm BEPtoPNS
T
comprises two parts, initialization (statementsst1, st2 and loop lp1, lines 4-11) and time expansion (statement st3 and loops lp2 and lp3, lines 12-53). Initially, for each node n∈N in G where ic
n
>0, it is transformed into a raw material r and is added to set R (lines 4 and 8). Initially, in loop lp1, for each raw material, r, the lower limit, Lr , and the upper limit, U
r
, are set, such that the total amount of materials available for the problem PNS
T
is defined. The complexity of the statement st1 is given by the number of nodes n∈N that meet the condition ic
n
>0 and the time required by loop lp1, which in the worst case is bounded by the expression | N | -k + 1 nodes. The above under the assumption that | N |-k represents locations that at the beginning of the emergency shelter people and k safety points outside the building (k> 1), where | | represents set cardinality. Finally, the product, SafetyPoint, is specified and added to the set P (statement st2, line 11). For the product, P
SafetyPoint
, algorithm BEPtoPNS
T
sets the lower limit L
PSafetyPoint
and upper limit U
PSafetyPoint
; such that the quantity of products to be manufactured is equal to the quantity of raw material demanded by the problem PNST. The number of people inside the building at the start of the emergency,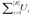 
, must be equal to the number of people evacuated (product, PSafetyPoint). Because the statement st2 describes assignments, its execution time is constant [15], [35-38] (see figure 3).
By assuming a limit to the evacuation time, T, algorithm BEPtoPNST generates materials Mi_(t+1) for 0 ≤ t < T; ; consequently, loop lp2 is executed T + 1 times (line 13). The material Mi_(t+1) represents the number of individuals present in i at time t + 1 (lines 18-19) ([8], p. 7). Subsequently, an operating unit o is created and added to set O for each i and t and operating units Oi_i_t_(t+1) are generated, where 0 ≤ t < T (lines 20-23). Similarly, the lower limit LO(i_i_t_(t+1) and upper limit UOi_i_t_(t+1) are set for each operating unit Oi_i_t_(t+1), such that algorithm BEPtoPNST specifies the number of individuals who prefer to stay in the specific location i for at least one unit of time, t + 1 ([8], p. 7). These instructions are executed T * (| N |-k) times. Subsequently, node j is transformed into material m and added to set M for each arc (i,j)∈A in G, where the value of capj ≠ ∞ o j is the only safety point (lines 24, 28-33). These operations are executed T * (| N |-k) * (| A |-1) times. Then, for each t, i, and j, operating unit o is created and added to O; algorithm BEPtoPNST generates operating units Oi_ j_t_(t+λijk)_k, where 0 ≤ t < T. In addition, the lower limit LO(i_ j_t_(t+λijk)_k) and upper limit UOi_ j_t_(t+λijk)_k are set for each operating unit Oi_ j_t_(t+λijk)_k (lines 34-37), such that algorithm BEPtoPNST specifies the number of evacuees moving from location i at time t to location j through corridor k at time t + λ_ijk ([8], p. 7). Similarly, these instructions are executed T * (| N |-k) * (| A |-1) times.
(8)
where clearly execution time g depends on G and T. Assuming that costs c i are constant [15],[35-38] and rearranging the terms of equation (8), equation (9) yields
(9)
By applying equation (9) to any size of G and T with constant c ≥ 12 , the complexity of BEPtoPNS T can be summarized in equation (10).
(10)
which is the expression of complexity for the worst case. It should be noted, as mentioned in [39], that the computational complexity of a PNS problem is of exponential order given by O(2 h ); where h represents the number of operating units. Thus, equation (11) shows that complexity grows exponentially with order O (T | A | (| N | -k)) + O (2 h )) in the worst case when solving a BEP.
(11)
where h is the sum of |O i_i_t_(t+1) |, |O i_ j_t_(t+λijk)_k) |, and |O evactime_t |.
3. DISCUSSION
Algorithm BEPtoPNST aims at transforming a BEP into a PNST problem by resorting to the P-graph method. However, it must be considered that the complexity involved in solving PNS problems is of exponential order as mentioned in the preceding section. Formally, it has been shown that the complexity of a PNS problem is equivalent to the set covering problem [40]. Because the set covering problem is one of Karp’s original 21 NP-complete problems, it can be inferred that the PNS problem is NP-complete [41]. This sort of problem can be addressed by using the P-graph method [27] because the method can drastically reduce the search space of a given PNS problem [27], [29].
Despite the computational cost of solving a BEP as a PNSTproblem (see equation (11)), the latter can be solved by resorting to the P-graph method which exploits the combinatorial nature of a BEP. Unlike other approaches, such as Hoppe and Tardos or algorithms CCRP and SSEP [14], the P-graph method provides not only the optimal solution (best evacuation route as a function of egress time), but also the best n suboptimal solutions [19]. In addition, the P-graph method can also model multiple starting locations and safety points, a feature not supported in SSEP [14]. The foregoing invites us to continue the work of reducing the computational complexity of solving PNS T problems in relation to BEPs.
4. CONCLUSIONS
This work analyzed the complexity of algorithm BEPtoPNST, which was found to be of order O(T|A|(|N|-k)) in the worst case with k > 1 safety points outside a building. Moreover, the algorithm’s computational complexity grows exponentially with order O(T|A|(|N|-k)) + O(2|h|) when solving a BEP, in the worst case. These results raise issues that deserve further research. First, the complexity of the entire process for finding at least the optimal solution to a BEP must be evaluated in terms of the minimum number of steps involved. The P-graph method with its five (5) fundamental axioms is able of reducing the search space; however, its complexity is of order O(2|h|) in the worst-case scenario. Therefore, it is required to analyze the average complexity [15], [35]. Second, it will be essential to design real-time monitoring systems for evacuation-route planning; such systems could require the adoption of modern computing techniques, e.g., Grid Computing, High-Performance Computing (HPC), and Internet of Things (IoT), to significantly accelerate its computation [42-44]. Finally, it will be necessary to evaluate the adoption of the strategy described in this work in other engineering fields. For instance, the design of Very-Large-Scale Integration (VLSI) circuits commonly faces problems that require the determination of optimal routes between the circuits that interconnect various electronic components, thereby implying the minimization of wiring length [45-48].
