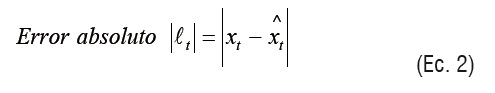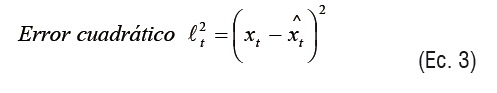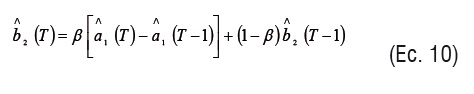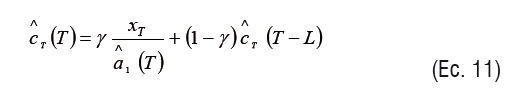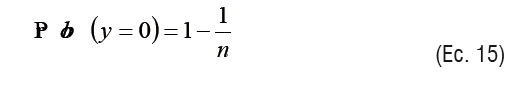¹ Magíster en Ingeniería. Docente titular. Departamento de Agroindustria. Facultad de Ciencias Agropecuarias. Universidad del Cauca. Colombia.

² Magíster en Ingeniería de Sistemas. Docente asociado. Escuela de Ingeniería Industrial y Estadística. Universidad del Valle. Colombia.

Correspondencia: smosquera@unicauca.edu.co

Recibido para evaluación: 05/10/2011 Aprobado para publicación: 20/06/2012

RESUMEN

Se presenta el típico problema de inventarios: excesiva cantidad de producto que no rota y poca del que rota, que se suma a la gran variedad de referencias y puntos de venta, dificultan la aplicación de modelos de pronósticos y la generación de políticas de inventarios. Se evaluó el comportamiento histórico de la demanda de los productos de consumo masivo en una cadena de suministro con una bodega y múltiples puntos de venta (One Warehouse N Retailer Problem) partiendo del análisis de la clasificación existente de los ítems para proponer una nueva con mayor cantidad de elementos de decisión; con base en lo anterior y mediante simulación, se eligió el método de pronóstico (promedio móvil, suavización exponencial simple, método de Croston, método de Winters) más apropiado para cada elemento y para cada una de las categorías considerando como factor de decisión el que obtuvo el menor coeficiente de variación. La investigación permitió concluir que, debido a las particularidades en la rotación y al comportamiento heterogéneo de la demanda de los productos en cada sitio de distribución, es conveniente realizar una clasificación por cada punto y definir modelos de pronósticos de manera individual.

PALABRAS CLAVE: Clasificación ABC, Cadena de abastecimiento, Inventarios, Logística.

ABSTRACT

The common inventory problem eventually arises: excessive quantities of product that do not circulate and a few of them that circulate that, along with the great variety of references and points of purchase, make difficult the application of forecasting models and the generation of inventory policies. The historic behavior of the mass consumption product demand in a supply chain with a warehouse and multiple points of purchase (One Warehouse N Retailer Problem) was evaluated. Starting from the analysis of the existing classification system of items a new proposal was made with a greater amount of decision-making elements based on the previous aspect and through simulation. The most appropriate forecasting method was also chosen (Moving average, simple exponential smoothing, the Croston method, the Winters method) for each element and for each one of the categories, considering as a decision factor the one that obtained the smallest variation of coefficient. The research allows to concluding that, due to the particularities in the product rotation and the heterogeneous behavior of the product demand in each place of distribution, it is convenient to carry out a classification for each point and to define forecasting models individually.

KEYWORDS: ABC classification, Supply chain, Inventories, Logistic.

RESUMO

Apresenta-se o típico problema de inventários: quantidade excessiva de produto que não é rotativo e alguns que o são, que somado à grande variedade de referências e pontos de venda, impede a implementação de modelos de previsão e a geração de política de inventários. Foram avaliadas as tendências históricas da demanda dos produtos de consumo em uma cadeia de fornecimento com um armazém e saídas múltiplas venda (One Warehouse N Retailer Problem) a partir da análise da classificação existente dos itens para propor uma nova com maior número de elementos de decisão; com base no exposto e por simulação, escolhemos o método de previsão (média móvel, suavização exponencial simples, método Croston, o método de Winters) mais adequado para cada elemento e para cada uma das categorias considerando como o fator decisivo o que teve o menor coeficiente de variação. O inquérito revelou que, devido às peculiaridades no comportamento de rotação e heterogênea da demanda para os produtos em cada local de distribuição, é conveniente classificar cada ponto e definir modelos de previsão individualmente.

PALABRAS-CHAVE: Classificação ABC, Cadeia de fornecimento, Estoques, Logística.

INTRODUCCIÓN

La investigación se enfocó en la revisión de la clasificación de los medicamentos para definir el modelo de pronósticos apropiado a aplicar en cada situación, considerando las diferencias existentes en los comportamientos de la demanda y de la dispensación en cada punto de distribución regional y elegir entre el trabajo por grupo de ítems, por zona geográfica o de manera individual. La complejidad de estos sistemas surge de la coordinación de las múltiples localidades y del impacto de una decisión en el resto de la cadena [1], aun si la demanda es determinística lo que convierte a la demanda en altamente errática aguas arriba, debido a [2]: emisión de órdenes anticipadas ante un crecimiento de la demanda, emisión de órdenes infladas cuando se presenta escasez, consolidación de órdenes para reducir costos fijos, variación de los costos de producción y/o compra.

Cadena de abastecimiento

El sistema es una cadena de abastecimiento con una bodega y N puntos de venta (One-warehouse N-retailer). En este caso el operador logístico posee 23 puntos de dispensación zonal, las compras surgen de la revisión mensual del inventario y la consolidación de los pedidos en la bodega, los cuales son despachados posteriormente hacia los puntos. En la bodega se presenta el típico problema: elevada cantidad de producto que no rota y baja cantidad de producto que rota, fenómeno impulsado por eventos internos y externos que demuestran la complejidad en el manejo. Los eventos internos son: no se aplican conceptos como lead time, punto de reorden y nivel de servicio; se da el mismo tratamiento a todos los productos sin considerar sus particularidades; inadecuado manejo de la información. Los eventos externos son: puntos de venta en regiones apartadas, pacientes de alto costo, recurrentes y con enfermedades terminales; demanda desigual en las regiones; cambios en el personal médico; incremento en el número de usuarios; problemas de orden público y ocurrencia de tutelas.

El elemento base para un apropiado tratamiento de estos casos es el manejo de la información precisa y en tiempo real en conjunto con la colaboración existente en la cadena de abastecimiento [3] para evitar errores en las decisiones de análisis de productos de manera consolidada o independiente y no afectar el modelo seleccionado de pronósticos y los niveles del inventario.

Clasificación ABC

Ordena los artículos según su participación en los costos y orientar los esfuerzos administrativos para su control [4]: ítems clase A tienen mayor proporción y requieren más atención; ítems clase B y C tienen menor representatividad y se tratan con menor rigurosidad. Facilita la función administrativa al definir categorías con base en criterios de costo (ventas) y no costo (eventos externos e internos) como los que ocurren en esta cadena de abastecimiento, tomando en consideración también la variabilidad de la demanda, como causas de generación de error en los pronósticos.

Error del pronóstico

Indica lo cerca que se halla el pronóstico de la demanda real [4] y se define mediante la ecuación 1 [5]:

Donde:
l_t = error del pronóstico en el periodo t;
x_t = demanda real en el periodo t;
^x_t = pronóstico para el periodo t, realizado algún tiempo antes.

Existen otras medidas [5] que han demostrado ser mejores que la anterior como son el Error Absoluto y el Error Cuadrático Medio (ecuaciones 2 y 3):

Desviación Absoluta Media, MAD. Expresa el error promedio (ecuación 4) sin importar si es positivo o negativo (entre más pequeño sea el valor positivo, mejor) [5]:

Cuando los errores tienen distribución normal, existe relación directa entre las dos medidas (ecuación 5), donde σ_e es la estimación de la desviación estándar de los errores:

Error Cuadrático Medio (ECM). Se monitorea para realizar ajustes a las constantes (señales de rastreo) si la proporción excede un límite (ecuación 6).

Se sugiere confiar en el mejor método de suavización sin considerar el ECM [6], aunque se ha comprobado el método con demanda intermitente y sugiere que cualquier medida de la exactitud puede ser excluida cuando una demanda es intermitente [7].

Modelos de pronósticos

El problema de una bodega y N puntos de venta cuenta con amplio tratamiento pero son pocos los reportes sobre aplicaciones de modelos de pronósticos en productos que se caracterizan por presentar dificultades logísticas y administrativas variadas como las que ocurren en este caso.

Pronóstico por Promedio Móvil. Sugerido para ítems clase C y posiblemente B [5] con demanda intermitente [7]; establece un promedio de la demanda pasada (patrón constante y pequeñas fluctuaciones) dando el mismo peso a las últimas N demandas: entre mayor sea N (entre 8 y 15), menor será el coeficiente de variación y el peso de los últimos datos, lo que no permite respuesta rápida [7]. En la ecuación 7, T es el periodo actual a partir del cual se calcula el promedio ( ), devolviéndose N períodos hasta el período T – N + 1.

Suavización Exponencial Simple. Ajusta los pesos de los datos pasados otorgando un valor α (0 < α < 1) a la última demanda y (1 - α) al pronóstico anterior con la ecuación 8 [5]:

Donde:

S_T = pronóstico al final del periodo T;
S_T-1 = pronóstico del periodo anterior;
x_T = demanda real;
α = constante de suavización;

S_T (promedio de las observaciones anteriores), es igual a la estimación anterior S_T-1, más α veces el error del pronóstico anterior, mientras que S₀ corresponde al promedio de los datos históricos sugeridos o utilizados [5].

Para la optimización de la constante de suavización , se sugieren valores entre 0,01 y 0,30 [5] o entre 0,05 y 0,20 [8, 9, 10] debido al contexto de demanda intermitente, eligiendo el que minimice la MAD o el ECM [5]. Se aplicó el método original y uno modificado en la industria de las telecomunicaciones por sus tendencias firmes y se comprobó que la suavización exponencial simple aporta mejores resultados [11]. Se simularon tres métodos [6]: suavización exponencial simple, suavización exponencial con tendencia corregida y método de Holt-Winters, concluyendo que el tipo de información disponible provee las bases para la selección del método.

Método de Holt-Winters. Para ítems con demanda estacional y requiere de valores de arranque para ^a₁(0), ^b₂(0) y ^c_T(0), utilizando datos históricos. Al final del periodo T, se revisa la estimación de la componente permanente con la ecuación 9 [5] donde 0 < α < 1 es una primera constante de suavización:

Luego, se estima la tendencia (ecuación 10):

Donde:

X_T = última demanda;
L= 12 periodo que cubre la estación;
L-T= componente estacional
m= datos históricos
0 < β < 1 = segunda constante de suavización.

Seguido, se estima el factor estacional para el periodo T (ecuación 11):

Donde

0 < γ < 1 = tercera constante de suavización.

Finalmente, se pronostica la demanda de cualquier periodo futuro (ecuación 12):

Método de Croston. Para ítems con demanda errática ó irregular con grandes fluctuaciones [7]. Cuando se asume una demanda de tipo Bernoulli, se propone el modelo de la ecuación 13 [8]:

Donde z_T es el tamaño de la transacción y:

Y_T = 1 si existe transsacción
Y_T = 0 si la transacción no ocurre

Se define un número de periodos entre transacciones (n) y, si la demanda es independiente del tiempo, la ocurrencia o no de una transacción tiene una probabilidad de ocurrencia 1/n (ecuaciones 14 y 15):

Si X_T = 0 no hay demanda y si X_T = 1 hay transacción, luego (ecuaciones 16 y 17):

Donde: n_T = periodos desde la última transacción; ^n_t valor de n al final del periodo t; ^Z_t promedio de la transacción al final del periodo t. Los valores de ^n_t y ^Z_t al inicio de la simulación se pueden asumir como el promedio de los datos históricos. Se puede requerir de reabastecimientos luego de una transacción, para lo cual es necesario calcular el pronóstico (ecuación 18):

El método de Croston es, por lo menos intuitivamente, superior al Promedio Móvil y la Suavización Exponencial [7]. Se han usado modelos adaptados de Holt-Winters y suavización [12] para pronosticar la demanda estacional de energía eléctrica durante el día, con resultados similares pero más precisos en la adaptación de Holt. Se comparó también el método original de suavización [11] con el modificado de Holt-Winters [13] en la industria de telecomunicaciones, con mejores resultados en el original por la eliminación de datos no pertinentes y perfeccionando los parámetros del modelo. Adicionalmente, se comparó por simulación [7], el comportamiento de cuatro métodos (Promedio móvil simple, Suavización Exponencial Simple, Método de Croston y una adaptación de este último) en 3,000 datos de demanda de automotores, con tres lead time, encontrando que el método adaptado de Croston arrojó un mejor desempeño con respecto a la MAD y el ECM.

MÉTODO

Información base para el desarrollo del sistema

Se usó información histórica mensual de demanda (cantidad formulada), oferta (cantidad despachada) y demanda no servida de los 1131 ítems distribuidos en los 23 sitios de dispensación, para un total de 26.013 SKU's; no se consideraron los que tuvieran menos de cuatro rotaciones por año y demandas de días especiales (ocasionales) porque afectan la medición e inciden sobre la confiabilidad de los resultados [12].

Clasificación de ítems

Por medio de una lluvia de ideas y el uso de un diagrama de Paretto, se hizo una cualificación y caracterización de los problemas relacionados con el manejo de los SKU’s en la empresa y se procedió a hacer una revisión de los criterios establecidos por la organización para la inclusión en cada categoría. Con base en los hallazgos, se propuso una nueva clasificación con elementos de decisión adicionales (de costo y de no costo), considerando la importancia de los medicamentos (incidencia sobre las ventas, rotación), las características de compra (localización y disponibilidad de proveedores, condiciones de la negociación) y dispensación (medios y condiciones de traslado) y las complejidades de su manejo en las regiones (localización geográfica, factores ambientales, complejidad en la entrega al usuario, contratos con EPS, tiempo de entrega al cliente, criterios para la realización de pedidos a la bodega central por parte de los puntos de entrega). Los elementos de decisión anteriores sirvieron para valorar la posibilidad de establecer la clasificación de los ítems por zonas geográficas o de manera individual, independientemente de donde se encuentre localizado el material.

Definición de los modelos de pronósticos

Se determinó la tendencia de la demanda de cada uno de los ítems de manera individual y por grupo, con el fin de definir el método de pronóstico a usar. Por simulación en hoja de cálculo de Excel, se determinaron los requerimientos futuros usando los métodos Promedio Móvil, Suavización Exponencial Simple, Holt-Winters y Croston, estableciendo comparaciones entre ellos para establecer el más apropiado, tomando como criterio de evaluación el que generó el menor error (desviación estándar de la MAD).

RESULTADOS

Clasificación actual de ítems

La clasificación se actualiza cada 3 meses con el base en el inventario físico sin considerar el costo dado que lo importante no es la utilidad sino la obligatoriedad en el suministro, por lo que la rotación es la que define la clasificación (cuadro 1), dado que su característica y comportamiento difiere (puede ser de baja rotación en un sitio, de alta rotación en otro o simplemente no existir).

Se sugirió redistribuir los productos en cuatro categorías (cuadro 1): AAA: productos hasta con un 20% de la rotación total en un sitio; A: entre 21% y 50%; B: entre 51% y 80% y C: entre 81% y 100%. Se observó que todos los productos clasificados en AAA también lo estaban en A, incluso hubo uno que estuvo presente en todas las categorías, dependiendo del lugar; además, varios productos AAA presentaron faltantes (cantidad formulada mayor que la cantidad despachada) con frecuencia, lo que permite intuir que su adquisición y dispensación no fueron controlados y no se consideraron los factores estacionales de la demanda, problemas que también fueron encontrados en la distribucimedicamentos [1].

Las diferencias entre las clasificaciones fueron bastante notorias, dado que en la propuesta se redujo sustancialmente el número de ítems importantes que pasó de 18,9% a 1,2%, en tanto que los menos importantes pasaron de 69,6% a 96,9%.

Modelos de pronósticos

Se observaron comportamientos híbridos (patrón de demanda diferente por periodo), lo que dificultó la determinación del método de pronósticos apropiado para cada ítem en cada sitio, lo cual justifica la no consolidación de items por zonas geográficas, dado que son unidades muy pequeñas que no deben cumplir funciones de un centro de distribución, lo que justificó el tratamiento individual por cada sitio, independiente de su clasificación.

Promedio móvil. De los 30 meses de información histórica, 12 datos (40%) se usaron para pronosticar y 18 (60%) para simular, con valores de N entre 8 y 15 periodos de tiempo y se eligió el que generó el menor coeficiente de variación (que para este caso fue N=12). En el cuadro 2 aparece la información para un ítem C, en donde se observa que el Promedio Móvil fue el método que arrojó los mejores resultados, coincidiendo con [7] que encontraron diferencias en los valores del pronóstico al usar este método con valores de N bajos.

Suavización Exponencial Simple. Para un ítem clase B el mejor valor obtenido de alpha fue 0,28, respondiendo bien a la tendencia creciente de la demanda (figura 1). Se realizó el mismo procedimiento con los demás métodos, corroborándose que el más asertivo fue el de suavización exponencial (cuadro 2). Cuando todos los puntos en el tiempo son considerados, se obtiene un mejor resultado con la suavización exponencial que con el Método de Croston [7], como en este caso donde los coeficientes de variación fueron de 0,474 y 0,771 respectivamente.

Autores coinciden en que la modificación al método de suavización arroja resultados más exactos que con la versión original cuando la estacionalidad es muy corta [12, 14], a diferencia de [11] que obtuvieron mejores resultados con el método sencillo y modificaciones en los parámetros de inicialización, siendo más sensible a la tendencia y con un coeficiente de variación menor.

Método Holt-Winters. La demanda de medicamentos está impulsada por variables difíciles de medir o que no han sido consideradas, como el clima, las epidemias, las brigadas de salud, el cambio de personal médico, el número de usuarios, los cuales pueden comportarse irregularmente o tener un factor estacional y de tendencia. En este caso no se tuvieron en cuenta medicamentos con rotación menor a 4 veces por año o aquellos destinados a pacientes terminales, lo que permitió promediar la demanda de un producto tipo A; pese a la escasez de datos y a los ajustes realizados, el método siempre se aproximó a la demanda real (figura 2). Con este método se obtuvieron mejores resultados que con Promedio Móvil, Suavización Exponencial y Croston dado que el coeficiente de variación fue ligeramente inferior (cuadro 2), lo cual coincide con lo reportado por [12].

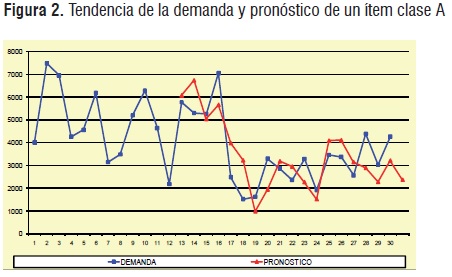
Método de Croston. No se encontraron diferencias significativas entre los resultados obtenidos con los métodos con una constante de suavización de 0,05 [7], mientras que en este estudio se obtuvieron mejores resultados con un alpha de 0,01 (cuadro 2) muy posiblemente influenciado por la poca cantidad de datos disponibles para el proceso. Para analizar la relación existente entre el coeficiente de variación y la irregularidad de la demanda, se promedió la información de 783 registros distribuidos en los 8 sitios más representativos y se concluyó que a mayor rotación, mayor es la irregularidad en la demanda; también, que entre mayor fue la rotación durante el año, menor fue el coeficiente de variación del pronóstico, debido a que cuando un producto rota de manera permanente, es mucho más fácil predecir su comportamiento (cuadro 3).

En términos generales, se encontró que la clasificación de un producto puede variar dependiendo de la zona geográfica en donde se distribuya y a lo largo del tiempo de valoración por el comportamiento de la demanda, por lo que el método para pronosticar debe ser modificado o ajustado de manera permanente; por ejemplo, cuando el Ácido Ascórbico tableta por 500 mg se clasificó como AAA se obtuvieron los mejores resultados con la utilización de Promedio móvil; cuando perteneció a la clasificación A, el mejor método fue Winters y cuando estuvo en B, Suavización Exponencial Simple y/o Winters.

Lo anterior obliga que el analista de inventarios realice el proceso de actualización de datos de manera permanente en el sistema de información para evaluar si el método sugerido en un periodo anterior se mantiene o si es necesario modificarlo. Estos modelos estructurados de manera sencilla han sido probados [4] en cadenas de abastecimiento similares con resultados puntuales que evidencian su confiabilidad y elevado grado de aplicación debido a que son sencillos y fáciles de manipular.

CONCLUSIONES

El criterio de dos rotaciones al año para la inclusión en la nueva categoría no es adecuado, porque no garantiza rotación y se corre el riesgo de que no sean formulados en periodos futuros y queden en inventario; la situación se torna más compleja si se contempla la dificultad para que estos productos roten en los establecimientos, por lo que se sugiere que cuando el producto rote menos de dos veces, se busque un proveedor local, rápido y confiable.

Generalizar un método de pronósticos por categoría ocasiona distanciamiento de éste con la demanda real, en la mayoría de los casos. La elección del mejor método está dada por diferencias muy pequeñas entre sus errores; ocasionalmente, al actualizar la información, la elección del método varía con respecto a un periodo de tiempo pasado. Los ítems C merecen tratamiento especial por ser muchos con baja demanda, un bajo costo o ambas cosas, por lo que se sugiere utilizar promedio móvil para su pronóstico y utilizar un período de pronóstico mensual.

AGRADECIMIENTOS

Los autores expresan su agradecimiento a las Universidades del Cauca y del Valle por los recursos facilitados, así como al operador logístico por su colaboración en el suministro de información que permitió adelantar tan importante labor.

[1] VIDAL, C.J., LONDOÑO, J.C. y CONTRERAS, F. Aplicación de modelos de inventarios en una cadena de abastecimiento de productos de consumo masivo con una bodega y N puntos de venta. Ingeniería y competitividad, 6 (1), 2004, p. 35-52.         [ Links ]

[2] SILVER, E.A., DAVID, P. and REIN, P. Inventory Management and Production Planning and Scheduling. 3 ed. New York (United States of America): John Wiley & Sons, 1998, 772 p.         [ Links ]

[3] LEE, H., PADMANABHAN, P. and WHANG, S. Information Distortion in a Supply Chain: the Bullwhip Effect. Management Science, 43 (4), 1997, p. 546-558.         [ Links ]

[4] VOLLMANN, T., BERRY, W., WHYBARK, C. y JACOBS, R. Planeación y control de la producción: administración de la cadena de suministro. 5 ed. México D.F. (México): Mc Graw Hill, 2005, p. 35-40, 36, 168.         [ Links ]

[5] VIDAL, C.J. Fundamentos de gestión de inventarios. 2 ed. Cali (Colombia): Universidad del Valle, 2003, p. 39, 46, 52-53, 73-76, 87.         [ Links ]

[6] BILLAH, B., KING, M., SNYDER, R. and KOELHER, A. Exponential smoothing model selection for forecasting. International Journal of Forecasting, 22, 2006, p. 239–247.         [ Links ]

[7] SYNTETOS, A. and BOYLAN, J.E. The accuracy of intermittent demand estimates. International Journal of Forecasting, 21, 2005, p. 303–314.         [ Links ]

[8] CROSTON, J.D. Forecasting and stock control for intermittent demand. Operational Research Quarterly, 23 (3), 1972, p. 289-703.         [ Links ]

[9] WILLEMAIN, T.R., SMART, C.N., SHOCKOR, J.H. and DE SAUTELS, P.A. Forecasting intermittent demand in manufacturing: a comparative evaluation of Croston’s method. International Journal of Forecasting, 10, 1994, p. 529–538.         [ Links ]

[10] JOHNSTON, F.R. and BOYLAN, J.E. Forecasting for items with intermittent demand. Journal of the Operational Research Society, 47, 1996, p. 121-131.         [ Links ]

[11] GARDNER, E. and DIAZ-SAIZ, J. Exponential smoothing in the telecommunications data. International Journal of Forecasting, 24, 2008, p. 170-174.         [ Links ]

[12] TAYLOR, J.W. An evaluation of methods for very short-term load forecasting using minute-by-minute British data. International Journal of Forecasting, 24, 2008, p. 645-658.         [ Links ]

[13] WINTERS, P.R. Forecasting sales by exponentially weighted moving averages. Management Science, 6, 1960, p. 324–342.         [ Links ]

[14] TAYLOR, J.W. and Mc SHARRY, P.E. Short-term load forecasting: an evaluation based on European data. IEEE Transactions on Power Systems, 22, 2007, p. 2213-2219.         [ Links ]