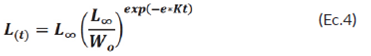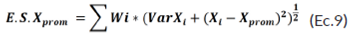INTRODUCCIÓN
Pseudoplatystoma orinocoense es un bagre dulceacuícola perteneciente a la familia Pimelodidae, endémica de la cuenca del río Orinoco [1]. En el río Orinoco se encuentra entre las especies más importantes desde el punto de vista pesquero y comercial junto con la especie Pseudoplatystoma metaense [1]. P. orinocoense es conocida comúnmente como rayao en Venezuela y Colombia.
En la pesca continental de Venezuela, P. orinocoense y P. metaense conforman conjuntamente 15,7% de la captura total desembarcada, con un promedio en la producción de 6121 ton/año entre 1996 y 2003 [2]. Particularmente en la región media del Orinoco se encuentran entre las más importantes en los desembarcos de la pesca artesanal, principalmente, P. orinocoense, con un 12,0% en la composición de las capturas, y unaproducción entre 8,8 y 23,1 ton/año, dependiendo del nivel del río [3,4].
En los desembarcos de los últimos años ha prevalecido la captura de tamaños relativamente pequeños de P. orinocoense debido a la selectividad del arte que generalmente se utiliza [5], que hace necesaria una evaluación de la población,donde la determinación de la edad y el crecimiento es una información básica [6].
En la región del Orinoco medio se determinó el crecimiento de P. orinocoense (sinónimo P. fasciatum) [7] a partir de datos retro-calculados a la formación de los anillos de crecimiento en la espina dorsal [8-11], quedando la incertidumbre en cuanto a los estimados de los parámetros de crecimiento, así como en los resultados de la evaluación de la población que demostró una sobrepesca del recurso [12], por haberse utilizado a priori el modelo de von Bertalanffy.
Hasta la fecha, los estudios publicados sobre el crecimiento de P. orinocoense y especies relacionadas se han realizado en base a la elección arbitraria del modelo de von Bertalanffy. Como los realizados en el río Apure en Venezuela con las especies P. orinocoense y P. metaense [13], en el río Cuibá de Brasil con la especie P. reticulatum [14] y en la Amazonia boliviana con P. punctifer y P. metaense [15]. Igualmente, los realizados en las especies P. metaense del río apure [2] y Pseudoplatystoma corruscans del río Cuiabá [16], y en otras especies [17-19]. La selección a priori del modelo de von Bertalanffy para el estudio del crecimiento no tiene en cuenta incertidumbres relacionadas con la estructura del modelo, y supone implícitamente la existencia de un modelo "verdadero”, una suposición considerada poco realista y no justificada desde el punto de vista filosófico y matemático [20].
En este sentido, se ha demostrado que el uso de la inferencia de modelos múltiples es una mejor alternativa en comparación con el uso a priori del modelo de von Bertalanffy [21], un enfoque adoptado actualmente por muchos autores [20,22-24], y considerado en el presente trabajo para determinar los parámetros de crecimiento de P. orinocoense.
En el trabajo se usaron tres grupos de datos que incluyeron los de longitud-edad observados según el número de anillos de crecimiento en la espina dorsal de P. orinocoense [7], el total de datos retro-calculados para todas las edades, y un subconjunto de datos retro-calculados que excluyeron a peces de uno y dos años de edad [7]; estos dos últimos grupos de datos fueron ajustados anteriormente seleccionando a priori el modelo de von Bertalanffy [7], que es precisamente el objetivo del presente trabajo, verificar o no el ajuste de estos datos a dicho modelo, usando además otros modelos de crecimiento para seleccionar realmente el de mejor ajuste.
La gestión efectiva de la pesca de P. orinocoense requiere del estudio detallado de su dinámica poblacional que incluye la estimación precisa de los parámetros de crecimiento [6], donde el uso de la inferencia de modelos múltiples constituye una mejor alternativa en comparación con la selección a priori del modelo de von Bertalanffy, como se venía haciendo hasta ahora [21].
En el uso de modelos múltiples para el estudio del crecimiento, los modelos de von Bertalanffy, Logístico y Gompertz generalmente han sido utilizados en sus formas tradicionales [20,22,24,29,30], con el inconveniente que presentan al manifestar diferentes interpretaciones de los parámetros de crecimiento [25,26], que limitan la estimación de un modelo promedio cuando el valor del peso ponderado de Akaike (W i ) así lo requiera [24]. Otra desventaja de la forma tradicional de dichos modelos es que no estiman otros parámetros de crecimiento considerados importantes, como el valor inicial de la curva W o . De allí que una mejor alternativa ante los modelos tradicionales es el uso de los modelos unificados de la familia U-Richards [25,26].
MÉTODO
A los datos de longitud-edad de P. orinocoense [7] se les realizó un ajuste no lineal, con ayuda del statgraphic 1.4, a tres modelos de crecimiento que incluyeron los modelos unificados U-von Bertalanffy, U-Logístico y U-Gompertz, derivados del modelo global U-Richards, según las siguientes ecuaciones:
Las versiones unificadas de los modelos U-von Bertalanffy y U-Logístico se alcanzaron sustituyendo al parámetro d de las ecuaciones 1 y 2 por las constantes d = 2/3 y d = 2 respectivamente [25]. En el caso del modelo U-Gompertz, d se calculó como un límite y no dándole un determinado valor [26], según las siguientes ecuaciones:
En las ecuaciones 1, 2, 3 y 4, L (t) = longitud teórica; L ∞ = longitud asintótica; t = edad; K = máxima tasa de crecimiento relativo en la inflexión de la curva; T i = edad en la inflexión de la curva; d = exponente o parte del mismo que controla el valor en la inflexión; W o = valor inicial de la curva (t = 0); e = número neperiano.
La clasificación y comparación de los modelos para seleccionar el de mejor ajuste se hizo utilizando el criterio de la información de Akaike (AIC) para muestras pequeñas (AICc) [20,22,26,27], según las siguientes ecuaciones:
donde, σ 2 = RSS n ; RSS suma de cuadrado residual de cada modelo, n el tamaño de la muestra, k el número total de parámetros de regresión estimados en cada modelo (incluyendo a σ 2 ), AIC c el AIC de cada modelo, AIC min el valor más pequeño del AIC c y ΔAIC C el grado de separación de cada AICc con relación al AIC min . AICc utiliza la función original que define el criterio de la información de Akaike (AIC), más un término adicional de corrección de sesgo que se usa generalmente cuando la relación 𝑛 𝐾 es pequeña (< 40) [22].
El modelo más parsimonioso o preciso en el ajuste de los datos fue el que presentó el valor mínimo del AIC (AIC min ), considerando que mientras mayor sea la diferencia entre el AICc de cada modelo candidato con relación al AIC min (ΔAICc), es menos probable que el modelo produzca un buen ajuste. En este sentido, se tiene como regla general que los modelos donde el ΔAICc es menor que dos (ΔAICc < 2), tendrán un apoyo sustancial de los datos y deben ser considerados al hacer las inferencias, además de indicar una correspondencia con el modelo más preciso (AIC min ). Cuando los modelos alcanzan un ΔAICc entre 4 y 7 (4≤ ΔAIC C ≤ 7) tendrán medianamente menos soporte de los datos. Cuando ΔAICc > 10 esencialmente no tendrán soporte alguno, o no explican una variación sustancial en los datos [20,28,29].
Para tener una mayor certeza en cuanto a la selección del mejor modelo, se calculó la plausibilidad de cada uno utilizando la ponderación de Akaike (Wi), según la siguiente ecuación:
donde, ∆i fue el ΔAIC c de cada modelo. De acuerdo al valor de Wi se consideró como el modelo más plausible o de mejor ajuste, aquel con valor mayor a 0,9 (Wi > 90%). Cuando los valores de Wi son menores a 0,9 (Wi < 90%), se supuso que ningún modelo fue superior a otro y se determinó un modelo promedio [20,29].
En el modelo promedio, la media del parámetro X ( 𝐿 ∞ , 𝐾, 𝑇 𝑖 , 𝑊 𝑜 ) se calculó usando la ecuación:
Mientras que el error estándar se estimó mediante la ecuación:
donde E.S.X prom es el error estándar del parámetro X, y 𝑉𝑎𝑟 𝑋 𝑖 la varianza del parámetro X, estimada del ajuste de los datos con cada modelo i [20].
RESULTADOS
Ante el inconveniente de los modelos tradicionales de von Bertalanffy, Logístico y Gompertz para la comparación de parámetros de crecimiento, el uso de los modelos unificados U-von Bertalnffy, U-Logístico y U-Gompertz, derivados del modelo genérico U-Richards, garantizan la selección de modelos que estiman valores realistas de dichos parámetros, además de una consistente interpretación y comparación [25,26].
Utilizando los datos observados de longitud-edad según el número de anillos en cortes de la espina dorsal de P. orinocoense [7], el ajuste no lineal de los modelos candidatos produjo estimaciones de los parámetros de crecimiento y estadísticos (RSS y R 2 ) representados en el Cuadro 1.
Cuadro 1 Parámetros y estadísticos de los modelos U-von Bertalanffy, U- Logístico y U-Gompertz.

ECVB = Modelo U-von Bertalanffy.
Los valores relativamente altos del R 2 , estimados para los modelos U-Logístico y U-Gompertz, en comparación con el estimado para el modelo U-von Bertalanffy (Cuadro 1), únicamente indicaron una mayor explicación de la variación de los datos y no de por sí un mejor ajuste, como se ha interpretado comúnmente [25,26,27]; en este sentido, fue más exacto y confiable el uso del criterio de información de Akaike (AIC) para seleccionar el modelo de mejor ajuste [20,22,23,24].
El AIC es un método reciente de selección de modelos matemáticos que utiliza la información Kullback-Leibler (distancia K-L) como medida conceptual de la distancia relativa de un modelo dado con relación al que en realidad describe la información contenida en los datos [29]. En este sentido, el modelo U-Gompertz fue el más preciso en el ajuste de los datos por presentar el valor mínimo del AIC (AICc min ); en correspondencia, además, con el modelo U-Logístico según el valor del ∆AICc (∆AICc < 2; Cuadro 2). El modelo U-von Bertalanffy no ajustó sustancialmente los datos por presentar un valor del ∆AICc mayor que 10 (∆AICc > 10), y una nula plausibilidad en el ajuste de los datos, de acuerdo al valor de W i (W i = 0; Cuadro 2).
Cuadro 2 Criterio de información de Akaike (AIC) y peso ponderado de Akaike (Wi) en los modelos U-von Bertalanffy, U-Logístico y U-Gompertz.
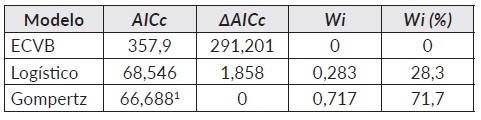
ECVB = Modelo U-von Bertalanffy; 66,6881 = A/Ccmin.
Según el AICc min y el valor del W i , el modelo que produjo un mejor ajuste fue el U-Gompertz (W i = 71,7%; Cuadro 2), pero sin una clara superioridad sobre el modelo U-Logístico (W i < 90%), por lo que se procedió a la estimación de un modelo promedio cuyos cálculos para el L ∞ se encuentran representados en el Cuadro 3.
Cuadro 3 Estimación del L ∞ en el modelo promedio entre el U-Gompertz y el U-Logístico.

L ∞ es = L ∞ estimado; Var = Varianza; EE = Error estimado; VI = Valor inferior; VS = Valor superior.
Los valores de los parámetros K, T i y W o correspondientes al modelo promedio, estimados siguiendo el mismo procedimiento usado para L ∞ , están representados en el Cuadro 4, con una curva de crecimiento en longitud de forma sigmoidea, representada en la Figura 1.
Cuadro 4 Promedio e intervalos de confianza de los parámetros de crecimiento estimados a partir de los modelos U-Gompertz y U-Logístico.

I.C. = Intervalos de confianza.
Los parámetros de crecimiento y estadísticos (RSS y R 2 ) estimados por los modelos candidatos ajustados a los datos retro-calculados para todas las edades (datos totales), y los retro-calculados que excluyen a las edades uno y dos (subconjunto), están representados en el Cuadro 5.
Cuadro 5 Parámetros y estadísticos estimados por los modelos a partir de datos retro-calculados.

ECVB = Modelo U- von Bertalanffy.
El ajuste no lineal de los modelos candidatos al total de datos retro-calculados demostró que el modelo U-Logístico no explicó variación alguna de los datos de longitud-edad según el R 2 (R 2 = 0), además de presentar valores no esperados (irreales) de los parámetros K y T i (Cuadro 5). Por tal razón, dicho modelo fue descartado de la inferencia de modelos múltiples, para evitar alteraciones en los resultados [20,22]. Entre los modelos U-von Bertalanffy y U-Gompertz el primero fue el más preciso en el ajuste de los datos, por presentar el valor mínimo (AIC min ) del AIC (Cuadro 6); mientras que el modelo U-Gompertz, no produjo un ajuste sustancial de dichos datos según del ∆AIC (∆AIC > 10) y el valor del W i (W i =0; Cuadro 6).
De allí que el mejor ajuste del total de datos retro-calculados lo produjo el modelo U-von Bertalanffy; un resultado que verificó los obtenidos anteriormente del estudio del crecimiento de P. orinocoense (P. fasciatum) [7], así como los resultados de la evaluación de la población a partir de estos resultados [12]. Los valores del L ∞ y K, estimados con el modelo U-von Bertalanffy (Cuadro 5) fueron aproximadamente igual a los estimados utilizando el modelo tradicional de von Bertalanffy para los mismos datos (L ∞ = 112,6; K = 0,080) [7]
Cuadro 6 Criterio de información de Akaike (AIC) de los modelos ajustados a los datos de González et al. (2010).

ECVB = Modelo U- von Bertalanffy; 609,61 y 424,31= AICmin
El R 2 estimado a partir del ajuste no lineal de los modelos candidatos aplicados al subconjunto de datos, que excluyó las edades de uno y dos años, demostró que los tres modelos candidatos explicaron adecuadamente la variación de los datos de longitud-edad (Cuadro 5); sin embargo, al contrario del ajuste de los datos totales, el AIC demostró que el modelo U-von Bertalanffy no ajustó sustancialmente dichos datos, según los valores del ∆AICc (∆AICc > 10) y el valor del W i (W i =0; Cuadro 6). Estos resultados comprobaron que un valor relativamente alto de R 2 no implica un buen ajuste de los datos, y que la selección más precisa del modelo de mejor ajuste se obtiene utilizando el AIC [25-27].
Al igual que con los datos de longitud-edad observados, que también excluyeron los peces de uno y dos años de edad, el modelo que produjo un mejor ajuste del subconjunto de datos fue el de Gompertz según el AIC min y el valor del W i (Cuadro 6), aunque sin mostrar superioridad sobre el modelo Logístico (W i < 90%), razón por la cual se procedió también a calcular un modelo promedio.
El valor del L ∞ que representó al modelo promedio en el subconjunto de datos fue de 75,0 (intervalo 44,1-105,9) cm de longitud total; el de K, 0,284 (intervalo 0,108-0,459) año-1; el de T i , 3,9 (intervalo 2,2-5,6) años y el de W o , 9,1 (intervalo 4,9-13,4) cm de longitud total, que fueron aproximadamente igual a los estimados en el trabajo a partir de los datos de longitud-edad observados (Cuadro 4).
Aparentemente, cuando se utilizan datos de longitud-edad que incluyen todas las clases de edades, el modelo de von Bertalanffy produce un mejor ajuste; mientras que en muestras donde faltan los peces más jóvenes (edades de uno y dos años), los datos de longitud-edad son mejor ajustados por otros modelos como el de Gompertz y el Logístico [20,29].
Los datos relativamente completos de longitud-edad facilitan el modelaje del crecimiento desde un tamaño inicial hasta uno asintótico, con una tasa de crecimiento gradualmente decreciente y sin punto de inflexión en la curva, como es característico del modelo de von Bertalanffy [7,17]. Posiblemente, el valor relativamente alto del T i estimado por el modelo U-von Bertalanffy en el conjunto completo de datos retro-calculados (T i = 22 años; Cuadro 5), se deba a la falta de puntos de inflexión en la curva de dicho modelo.
La selección del modelo de mejor ajuste no sólo depende del patrón de crecimiento de la especie, sino también de la calidad y las características del conjunto de datos en cuanto a la información que contienen, donde el objetivo del AIC no solo es modelar los datos, sino también poner de manifiesto esta información [21,28].
Cuando la información de los datos incluye solamente peces juveniles, como en el caso de las lagunas de la confluencia de los ríos Solimões y Japurá del estado de Amazonas en Brasil, los datos no soportan bien el modelo de von Bertalanffy y se ajustan mejor a otros modelos como el Logístico y de Gompertz [20]; sin embargo, datos compuestos en su mayor parte por peces adultos, tampoco se ajustan bien al modelo de von Bertalanffy [20], como en el caso que nos atañe.
Gran parte de los estudios del crecimiento en peces se han realizados utilizando a priori el modelo de von Bertalanffy y generalmente con datos provenientes de la pesca artesanal, donde se ven afectados los estimados de los parámetros de crecimiento por la ausencia en los datos de peces muy jóvenes o muy viejos, debido a la selectividad de las artes de pesca [29]. Cuando los datos provienen de la pesca artesanal, es recomendable, por lo tanto, usar más de un modelo de crecimiento para seleccionar el que mejor describe la información de los datos disponibles, en lugar de estudiar el crecimiento en base al modelo único de von Bertalanffy.
En este sentido, es necesario revisar algunos trabajos como los realizados en P. reticulatum en la cuenca del río Cuiabá [14] y P. punctifer en la Amazonia boliviana [15], en las especies P. corruscans y P. tigrinum de la cuenca del río Cuiabá [16] y de la Amazonia boliviana [15] respectivamente, así como en P. metaense del río Apure en Venezuela [2], principalmente, si los estimados de los parámetros de crecimiento han sido utilizados para evaluar las poblaciones usando métodos como el de Beverton y Holt, el cual es muy sensitivo a los valores de L ∞ y K [12].
CONCLUSIONES
Los trabajos que hasta ahora se han hecho sobre el crecimiento de los bagres del Género Pseudoplatystoma han utilizado al modelo de von Bertalanffy como modelo único, seleccionado a priori, sin tomar en cuenta que dicho modelo solo se ajusta a datos que incluyen todas las edades. En datos provenientes de la pesca artesanal, donde por efecto de la selectividad los peces jóvenes y los más viejos están excluidos, los modelos Logístico y de Gompertz son los que producen un mejor ajuste; no siendo suficiente utilizar solo el coeficiente de determinación R 2 para estimar el modelo que produce un buen ajuste, sino usar el criterio de la información de Akaike (AIC), que toma en cuenta el tipo de información contenida en los datos.