Introducción
La cognición de las 4E es una tendencia teórica reciente que trata de explicar los fenómenos psicológicos enfocándose en su naturaleza situada. La idea es que la mente humana se constituye en la interacción con otras personas y con el mundo, esto es, en situaciones sociales (Newen et al., 2018). Los términos de las 4E (extended, enactive, embedded, embodied) describen diversos aspectos que los investigadores han ido reconociendo en la vida mental cotidiana.
De una manera más precisa, se dice que la mente humana está extendida (extended) porque nuestra especie deposita información en artefactos culturales que así se convierten en herramientas mentales que usamos para cargar y descargar parte del trabajo cognitivo en configuraciones (affordances)1 del entorno (Smart, 2018). Del mismo modo, apuntar al carácter enactivo (enactive) de la cognición implica atender al hecho de que la mente implica fenómenos estrechamente conectados con la actividad en tiempo real, con lo que sucede aquí y ahora, de manera que las condiciones específicas de tiempo y espacio son relevantes para entender la naturaleza de dichos fenómenos (van Dijk & Myin, 2019). Adicionalmente, es necesario reconocer la relación intrínseca entre la actividad compartida y la creación de ámbitos de racionalidad o actividad dentro de los cuales los fenómenos mentales de las personas se articulan con prácticas, saberes y costumbres sostenidos de manera conjunta por quienes pertenecen a una tradición cultural; es por ello que es importante notar que cada fenómeno mental se halla incorporado (embedded) a dicha estructura interactiva que trasciende la subjetividad individual (Chavarria & Orozco, 2006). Asimismo, es importante notar que en todo caso se trata de fenómenos que se actualizan en la práctica, por lo cual suponen toda una serie de despliegues corporales, en los que la estructura y calidad del movimiento, el gesto y, en general, las manifestaciones del cuerpo (embodied) son relevantes para entender la subjetividad de los agentes involucrados (Gallagher, 2017).
Existe una gama amplia de preguntas significativas en psicología que se pueden formular sobre la base de las ideas de la cognición de las 4E. En los últimos años los investigadores del ámbito de la psicología educativa han hallado conexiones muy fructíferas entre las ideas de las 4E y los conceptos que explican el aprendizaje y el desarrollo cognitivo; especialmente, cuando los interrogantes decisivos se enfocan en un ambiente de aprendizaje (el aula) dentro del cual se lleva a cabo la actividad sociocultural de enseñanza-aprendizaje. Así pues, en concordancia con todo lo anterior, vale la pena describir cómo la investigación reciente ha incorporado las ideas de la cognición de las 4E en la indagación sobre el aprendizaje matemático.
Este objetivo resulta mucho más acuciante dadas las circunstancias de la pandemia de covid-19 a nivel mundial, las cuales supusieron una ruptura en las formas de socialización habituales de la escuela (Cardini et al., 2020). Si se analizan las consecuencias de la pandemia en la socialización desde el enfoque 4E, puede notarse que el aislamiento no afectó solamente la comunicación fluida entre maestro y estudiante, lo cual puede estar estrechamente relacionado con la dinámica enactiva en tiempo real del aprendizaje, sino que, además, implicó una reorganización profunda de toda la actividad educativa en las otras facetas mencionadas. Así, por ejemplo, en la faceta extendida, los arreglos didácticos tradicionales del aula (lápices, cuadernos, libros, diagramas, etc.) fueron relegados a un segundo plano para privilegiar el uso de objetos interactivos de aprendizaje; ello instó a los maestros a reconfigurar sus estrategias pedagógicas dentro de ambientes virtuales (Hu et al., 2021; Sullivan et al., 2020). El marco sociocultural mismo del aprendizaje (embeddded) se reestructuró de manera tal que buena parte del contexto de las situaciones de aprendizaje requiere ahora la interacción con plataformas e interfaces virtualmente soportadas (Ruiz-Palmero et al., 2016). Evidentemente, todo esto implicó una transformación de la actividad corporal (embodied) de los aprendices, quienes, repentinamente y por razones originadas en el contagio, empezaron a pasar más tiempo frente sus ordenadores, con consecuencias desconocidas para su salud física y mental (Spiteri, 2021).
De manera particular, en el contexto de la educación matemática, el impacto de la pandemia en las prácticas de enseñanza-aprendizaje tuvo repercusiones valoradas de manera tanto negativa como positiva. En el primer caso, los docentes reportaron dificultades en la atención de los estudiantes a los contenidos matemáticos en modalidad virtual, inasistencia o fallos en la conectividad, que generan una disminución en el rendimiento académico en matemáticas, lo que se conoce como Covid Slide (caída de covid) (Scott, 2021). Para ilustrar este fenómeno, Kuhfeld et al. (2020) calcularon que en otoño de 2020 los estudiantes que no recibieron instrucción remota durante primavera ingresarían con solo el 37 % a 50 % de los logros de aprendizaje en matemáticas. Asimismo, las interacciones docente alumno estuvieron comprometidas tanto en términos de poca programación de espacios de tutoría o apoyo académico como en la expresión de una faceta afectiva negativa caracterizada por estrés académico e incremento de ansiedad o fobia a las matemáticas por parte de estudiantes y padres de familia (Scott, 2021). En el segundo caso, la pandemia permitió a los docentes de matemáticas de básica primaria y secundaria visibilizar «nuevas formas de enseñar y aprender, como la televisión (TV) y las aplicaciones educacionales que ganaron el espacio en la nueva configuración social, donde maestros, profesores, familiares y estudiantes pasaron a vivir nuevos contextos de hacer escuela» (de Souza, 2021, p. 149).
Teniendo en cuenta este panorama, las teorías de la cognición 4E pueden brindar un marco amplio para entender la transición que conduce de un modelo de educación predominantemente presencial a otros que seguramente se instaurarán en la pospandemia, en los que predominará algún grado de virtualización de la actividad conjunta. La transformación que está en juego implica repensar cómo es que la educación conduce a cambios físicos y psicológicos en los niños; así, por ejemplo, para el caso de la percepción:
En general, se considera que la educación cambia el conocimiento y la comprensión de un niño. Lo que puede resultar menos obvio es que la educación transforma la percepción del niño. Vygotsky teorizó el desarrollo de la percepción como una transformación de formas reales (o ingenuas) a ideales (o culturales) (…). La transformación ontogenética de la percepción a partir de su forma ingenua ha adquirido diversos nombres en la literatura de investigación educativa: visión profesional (Goodwin, 1994) apunta al contexto de un dominio de escrutinio así como la práctica discursiva en la que emerge la percepción; la percepción disciplinada (Stevens & Hall, 1988) agrega la cualidad moral de ser formado por otros; la percepción educada (Goldstone et al., 2010) se refiere a la transformación de la percepción de arriba hacia abajo cuando aprendemos a percibir algo de acuerdo con las necesidades cognitivas de nivel superior; y la percepción teórica (Radford, 2010) se refiere a la idea marxista de la práctica social que transforma los sentidos humanos. (Shvarts & Abrahamson, 2019, p. 3)
Como puede verse en la cita anterior, la educación introduce cambios profundos, aún si examinamos solamente una de las facultades psicológicas de los seres humanos.
Las aristas desde las cuales se pueden examinar esas metamorfosis son muy diversas (Pérez Jiménez, 2016). El enfoque de la cognición 4E tiene el potencial para suministrar una red de conceptos interrelacionados que configuren un marco con el cual estudiar esas transformaciones psíquicas producto del aprendizaje; ello sin aislar cada fenómeno, faceta, suceso o interacción relevante de otros con los cuales está intrínsecamente relacionado.
Así pues, en este caso, vale la pena conocer cómo se ha venido indagando el desarrollo de habilidades y conceptos en el aprendizaje de la matemática inicial desde puntos de vista inspirados en las teorías 4E. La consigna principal de los investigadores parece ser que «los conceptos matemáticos abstractos se forman y se comprenden haciendo inferencias a través de la comprensión estructural durante las acciones y experiencias físicas del niño» (Moyer-Packenham et al., 2019, p. 330). En suma, la pregunta central que orienta este estudio apunta a establecer cómo se han adaptado las ideas de la cognición situada 4E para el estudio del aprendizaje de las matemáticas en la investigación contemporánea, de manera que pueda proporcionar estrategias para la cualificación de los procesos pedagógicos y didácticos en las aulas en tiempos de pospandemia.
Método
Estrategia metodológica
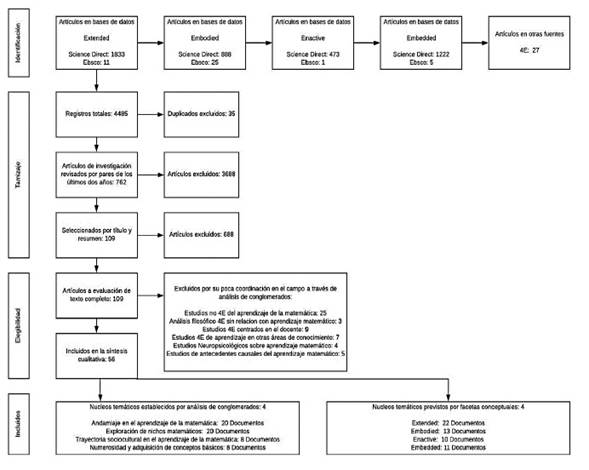
Se realizó una indagación documental que atiende a la investigación reciente en el área; para ello se implementó una estrategia de revisión sistemática con síntesis cualitativa, siguiendo las fases de: a) identificación de los recursos disponibles; b) tamizaje de los documentos encontrados según criterios; c) selección de los recursos a incluir de acuerdo con el contenido; y d) elaboración de una síntesis comprensiva de las investigaciones recientes sobre el tema (Snyder, 2019).
Procedimiento
La revisión se realizó cubriendo el rango de los últimos cuatro años. La indagación en bases de datos se llevó a cabo en dos momentos (14 de septiembre de 2020 y 28 de octubre de 2021), lo cual permitió seleccionar de una manera más fiable los documentos por la comparación de registros. La búsqueda se realizó en las bases de datos Science Direct y Ebsco Academic Search Ultimate; se mantuvo abierta la posibilidad de agregar recursos encontrados en otras fuentes.
Para la búsqueda se introdujo el script Mathematics AND Situated AND Cognition AND Learning AND (Extended, Enactive, Embodied, Embedded). Es decir, se mantuvieron los términos básicos de la búsqueda sobre ideas de cognición situada en el aprendizaje de la matemática, alternándolos con los términos de las 4E. La idea era distribuir de manera anticipada los recursos encontrados en las cuatro categorías correspondientes a cada una de las facetas conceptuales de la cognición de las 4E.
Para el tamizaje se aceptaron los documentos que presentaran investigaciones en psicología y educación o artículos conceptuales relacionados con la temática de interés. Se excluyeron: a) otras revisiones documentales; b) capítulos de libro; y c) notas editoriales y textos que no son resultado de investigación. Durante la selección se aplicaron otros criterios de exclusión, dirigidos a garantizar al máximo que los documentos seleccionados trataran sobre investigación del aprendizaje de la matemática en cognición 4E centrados en el aprendiz (figura 1). Para ello se aplicó el procedimiento de análisis de conglomerados bajo el criterio de palabra repetida, extrayendo las 20 palabras más frecuentes con una longitud mínima de cuatro caracteres y se examinó el contenido de los conjuntos hallados, de modo que se dejaron por fuera aquellos grupos de documentos que atendían solo colateralmente al tema en cuestión.
Plan de análisis
Se aplicó análisis de conglomerados para encontrar una configuración final que permitiera hallar núcleos temáticos en torno a los que se articula la discusión entre los investigadores del área. Para la síntesis cualitativa se examinaron de manera detallada 56 artículos (54 en idioma inglés y 2 en español) que cumplieron los criterios mencionados, atendiendo a su coordinación en esos núcleos temáticos y en las facetas de las 4E. Se obtuvieron nubes de palabras con los artículos en inglés para cada componente de las 4E, a fin de caracterizar los términos más frecuentes, así como mapas jerárquicos para establecer relaciones entre nodos (términos clave) y facetas de las 4E. Todos los análisis se realizaron en Nvivo 11.
Resultados
En cuanto a características de identificación de los 56 artículos obtenidos, 43 de ellos (76.78%) se sitúan entre 2018 y 2021. Los 13 restantes se ubican entre los años 2005, 2010, 2012-2017 y 2022, esto teniendo en cuenta que los artículos conceptuales y empíricos de estas fechas presentan acercamientos iniciales al estudio de las 4E; de ahí la importancia de caracterizar el fenómeno desde sus comienzos.
Con relación al país de procedencia de los autores, 31 artículos provienen de Estados Unidos, seis del Reino Unido, cuatro de Australia, tres de Alemania, Israel y Canadá, dos de Finlandia e Italia y con un artículo aparecen los siguientes países: Brasil, Chile, Colombia, Corea del Sur, Suecia, Polonia, España, Países Bajos y Rusia.
A nivel metodológico, 19 de los 56 artículos corresponden a estudios experimentales, nueve a estudios observacionales, ocho son de estudios de caso, siete artículos son conceptuales y seis aluden a intervenciones educativas. También se obtuvieron estudios de corte predictivo, longitudinal, análisis de contenido y de discurso, con dos artículos cada uno, así como un artículo de análisis temático. Hay que apuntar que 41 de las investigaciones incluidas son estudios acerca del aprendizaje infantil. Entre los participantes de las investigaciones están estudiantes de preescolar, básica primaria, de díadas infantes-padres, docentes en servicio y practicantes de carreras de matemáticas o afines que están en proceso de formación para la posterior a enseñanza a infantes y jóvenes (anexo 1).
El análisis de conglomerados arrojó cuatro núcleos temáticos que agrupan los 56 documentos seleccionados para la síntesis final (figura 2). Se trata de temas que son transversales dentro del campo de estudio de la educación matemática y que se revelan como tendencias interesantes de estudio en conexión con las ideas de la cognición situada.
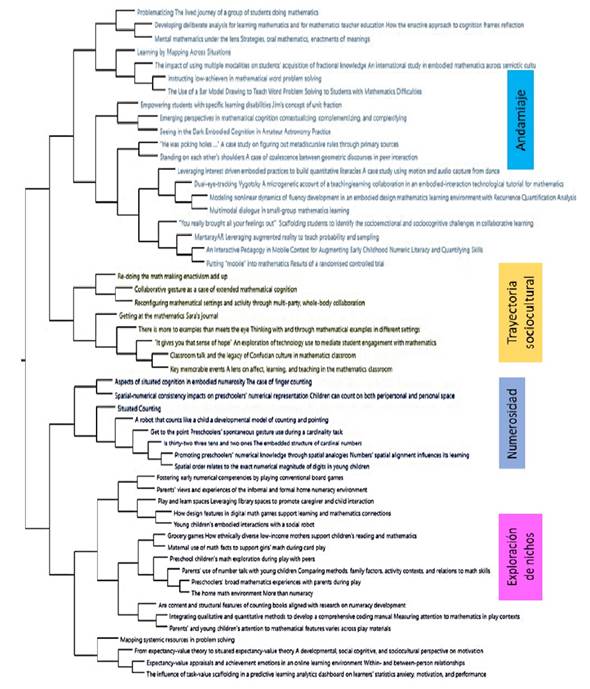
Figura 2 Recursos conglomerados por similitud de palabra, configuración final de 4 núcleos temáticos
Los núcleos temáticos son:
Andamiaje
El uso de tecnologías y objetos culturalmente dispuestos para el aprendizaje orienta el primero de los núcleos temáticos hallados. El andamiaje es un proceso psicosocial en el que otros individuos y el entorno compartido brindan soporte al aprendiz de una manera que propulsa decisivamente su desarrollo intelectual, afectivo e incluso físico (Krueger, 2011). En el caso del aprendizaje infantil de la matemática, es un hecho que la cognición del niño se nutre de sus experiencias con objetos culturalmente diseñados para facilitar su acceso a conceptos (ábacos, reglas, libros, dispositivos electrónicos, etc.). Del mismo modo, hay unas personas (maestros, padres, etc.) que se esfuerzan activamente en crear oportunidades de aprendizaje y generar situaciones (tareas) que, desde su punto de vista, conducen al desarrollo de conceptos matemáticos.
Una de las indagaciones más interesantes emprendida por los estudios 4E actuales, y definitivamente crucial dadas las condiciones que derivaron de la emergencia sanitaria, consiste en establecer el modo en el que las tecnologías de la información y la comunicación pueden fomentar el aprendizaje; verbigracia, establecer en qué medida artefactos como los teléfonos celulares pueden servir de andamiaje para el aprendizaje. La idea es promover una integración digital en la que el niño aprende a ser un usuario activo en plataformas interactivas: «Las técnicas de aprendizaje móvil han aportado el potencial de estructurar (scaffolding) la información en un contexto del mundo real que permite a los alumnos interactuar más activamente con su contenido de aprendizaje» [énfasis añadido] (Mowafi & Abumuhfouz, 2021, p. 1541).
En esa misma vía, el potencial educativo del andamiaje tecnológico está generando una transformación que insta a los maestros a cambiar los modelos pedagógicos centrados en la transmisión de conocimiento por otros en los que el eje principal es la participación en actividades interactivas conjuntas dentro de ambientes de realidad aumentada. Los estudios muestran que el diseño de ambientes de aprendizaje que incluyan objetos interactivos en entornos de realidad aumentada puede mediar efectivamente el aprendizaje:
La participación activa en la actividad de aprendizaje facilitó la inclusión de los conocimientos, actitudes, hábitos e intereses previos que los estudiantes aportaron a la experiencia. Los estudiantes que participan en experiencias de aprendizaje aumentado pueden aprovechar el marco de la actividad y su propio conocimiento e imaginación a medida que la experimentan. Ellos tienen la capacidad para actuar y responder como si la actividad de aprendizaje fuera real, incluso si hay muy poco apoyo visual explícito para soportar la metáfora de esa actividad. (Conley et al., 2020, p. 19)
En concordancia, y en relación con las condiciones exigidas por el marco de interacción virtualizada, parece necesario transformar la mediación pedagógica trayendo al centro de la reflexión del docente tanto una evaluación del potencial comunicativo de las estrategias de enseñanza junto como la estructuración de los objetos incluidos durante las actividades de aprendizaje. Así pues, para la preparación de la clase del docente contemporáneo resulta tan importante atender a la estructura de los argumentos y contenidos a desarrollar como a la infraestructura de plataformas, objetos virtuales, recursos y apoyos didácticos que se van introducir dentro de la sesión de aprendizaje. En palabras de los investigadores hay que atender al acto pedagógico como una actividad multimodal:
Proponemos una lente analítica que combina el aprendizaje dialógico y el diseño corporeizado. Esta lente analítica expande la noción de diálogo como una actividad multimodal. En consecuencia, nos parece imperativo explorar cómo un diálogo multimodal se manifiesta en el aprendizaje en otros contextos dentro y fuera de la Educación Matemática. El uso de estas dos teorías en conjunto también puede ilustrar el aprendizaje corporeizado de grupos pequeños dentro de un contexto social realista como sucede en el caso del aula. (Abdu et al., 2021, p. 10)
Es claro que enfatizar la importancia de la mediación durante el aprendizaje es un asunto ya ampliamente reconocido antes de las teorías 4E; lo que resulta novedoso es atender al potencial educativo del diseño de objetos (extended), el marco social y tecnológico (embedded), las dinámicas en tiempo real (enactive) y el ajuste de la actividad al movimiento/cuerpo del aprendiz (embodied).
Trayectoria sociocultural
Tiene que ver con que los aprendices atraviesan un proceso de enculturación (Heft, 2013), el cual les permite introducirse de manera progresiva como participantes de las prácticas socioculturales que se desarrollan dentro de la escuela o de la comunidad respecto de la matemática. De acuerdo con Barnett et al. (2021), se trata de una adquisición en la que el individuo se ajusta progresivamente desarrollando una sensibilidad que le permite reconocer patrones propios de las actividades en las que participa:
A medida que los novatos se involucran en actividades que les otorgan acceso a las prácticas de los veteranos, «van formando gradualmente una idea general de lo que constituye la práctica de la comunidad» (p. 95). Es a través de tales acciones participativas que los estudiantes son enculturados en una comunidad de práctica (Brown et al., 1989), donde esta enculturación «incluye una comprensión cada vez mayor de cómo, cuándo y sobre qué colaborar con los veteranos en qué se confabulan o chocan, y lo que se disfruta, no les gusta, respetan o admiran» (Barnett et al., 2021, p. 3).
Un aspecto importante de ese proceso es que implica una dinámica de mutuas transformaciones en las que son modificados tanto el aprendiz, como los expertos y, de manera simultánea, los objetos y ambientes de aprendizaje. Esa dinámica compleja crea patrones estables de actividad que se pueden caracterizar mejor atendiendo a las trayectorias individuales y compartidas de los participantes:
Conceptualizamos la relación dialéctica entre la actividad y el espacio producido socialmente como necesariamente infundida con acción, interacción, práctica y experiencia corporales. La multiplicidad del espacio, de trayectorias e historias coexistentes en curso (Massey, 2005) es una multiplicidad de seres encarnados que se mueven juntos en actividad. (Kelton & Ma, 2018, p. 182)
Atendiendo a esta idea, el aprendizaje de la matemática inicial ocurre gracias a la integración del individuo en esta dinámica intersubjetiva y con el entorno. Se trata de una forma de coordinación en la que se intercambian ideas en un espacio intersubjetivo recreado continuamente. El ambiente de aprendizaje esta imbuido con posturas, sensibilidades y criterios que los participantes traen, además de configuraciones preexistentes propias de su nicho cultural a las cuales pueden atender cuando perciben directamente los objetos de aprendizaje. Así, por ejemplo, el estilo del docente genera formas específicas de acercamiento propias de cada tradición social:
La re-expresión crea una atmósfera en la que los estudiantes se sienten cómodos para presentar y comunicar sus propias ideas matemáticas de una manera lógica/razonable y, por lo tanto, para sacar conclusiones. Los estudiantes co-construyen el conocimiento matemático de una manera armonizada y respetuosa basada en la filosofía del neoconfucianismo coreano. (Sum & Kwon, 2020, p. 9)
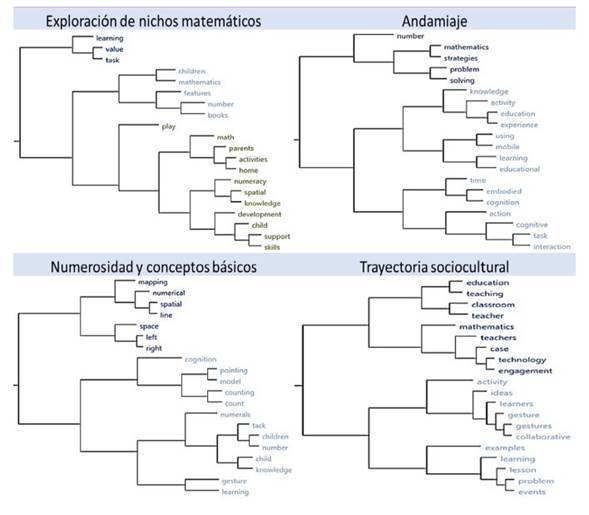
En esa medida la unidad de análisis del aprendizaje propuesta por los estudios de cognición 4E deja de ser el individuo aislado que adquiere conocimiento. Incluso la mera interacción entre individuos abstraída del entorno (por ejemplo, el intercambio de mensajes sin atender al contexto) resulta ser demasiado precaria para la complejidad estudiada; la unidad de análisis propicia es más bien el aula entendida como un nicho enriquecido de affordances en el que interactúan estudiantes y maestros. La figura 3 nos muestra la importancia del aula (classroom) y la preponderancia de la actividad en el análisis de la trayectoria sociocultural. Esta figura permite visualizar también las relaciones de este núcleo temático con los otros tres hallados mostrando las palabras más recurrentes en cada núcleo.
Numerosidad y adquisición de conceptos básicos en matemáticas
Dado que una amplia mayoría de las investigaciones seleccionadas se centran en el aprendizaje infantil de las matemáticas, resulta obvio que uno de los núcleos temáticos en el área sea precisamente establecer cómo es que los niños adquieren conceptos básicos del área. El advenimiento de las habilidades y conceptos para trabajar con números (numerosidad) se halla entre esos asuntos centrales de la investigación reciente. Desde hace unas décadas, la explicación dominante acerca de cómo es que los niños aprenden los números asume que se trata de un aprendizaje que sucede en virtud del desarrollo de procesos representacionales abstractos (función de sucesión, principio de cardinalidad, etc.) en la mente del infante. La investigación en cognición 4E ha revolucionado el área mostrando que la capacidad para tratar con entidades matemáticas abstractas (números, líneas, puntos, etc.) puede estar más bien relacionada con el desarrollo de la habilidad para mapear objetos de la práctica de aprendizaje (mapping). En palabras de los investigadores: «Por tanto, cuando se trata de la adquisición de conceptos numéricos, es razonable suponer que la adquisición se basa directamente en la estructura de las representaciones externas de los números» (Guerrero et al., 2020, p. 12).
Es importante notar que la descarga representacional es una diferencia crucial entre los dos tipos de explicaciones. Los estudios anteriores suponían el desarrollo de una serie de funciones o procesos cognitivos altamente especializados para las tareas matemáticas más sencillas (contar, sumar, restar, etc.), lo cual implicaría que para la resolución de tareas simples la memoria de trabajo del individuo debería tener el poder de cargar toda la información relevante. En los estudios adeptos a la cognición situada se asume que una parte importante del trabajo cognitivo es directamente perceptual; es decir, el niño aprende a tratar con configuraciones y disposiciones de objetos culturalmente dispuestos, lo cual disminuye los requerimientos postulados sobre la memoria de trabajo del infante:
Sugerimos que algunos de estos pasos pueden ser facilitados por la organización externa de la situación de conteo. Utilizando los métodos de cognición situada, analizamos cómo el equilibrio entre las representaciones externas e internas implicará diferentes cargas sobre la memoria de trabajo y la atención del individuo que cuenta. (Gärdenfors & Quinon, 2020, p. 1)
En breve, la habilidad para mapear cantidades sobre la base de los affordances socioculturales percibidos (números, conjuntos, líneas, etc.) se desarrolla progresivamente a medida que el infante participa en prácticas matemáticas con pares y docentes. Los poderes perceptuales del infante cuentan con la estructura de los arreglos culturales (líneas, direcciones, numerales, etc. Figura 3) para llevar a cabo las actividades, generando una sensibilidad cada vez mayor a los números (numerosidad). Recíprocamente, la configuración física de los ambientes de aprendizaje sirve de andamio al desarrollo conceptual.
Uno de los estudios seleccionados es claro al respecto: «Nuestros resultados sugieren que el orden espacial de los dígitos puede actuar como una fuente poderosa de información de magnitud que los niños pequeños usan para el andamiaje de la representación mental de números exactos» (Sella et al., 2019, p. 401).
Exploración de nichos matemáticos
Las teorías 4E suponen en realidad una interacción fluida entre las personas dentro de ambientes arreglados socialmente para la práctica; en esa medida, hay una conexión estrecha entre las ideas de la psicología ambiental-ecológica, la filosofía de la mente y las teorías 4E (Szokolszky & Read, 2018). La convergencia principal está relacionada con una manera de concebir el ambiente, según la cual es un nicho enriquecido socioculturalmente pleno de posibilidades de acción (affordances) disponibles para los individuos de nuestra especie (Heras-Escribano & de Pinedo-García, 2018). Así las cosas, pensar los ambientes de aprendizaje de la matemática en una perspectiva 4E supone atender a las diversas configuraciones físicas y sociales que determinan las prácticas de enseñanza y aprendizaje; se trata de verdaderos nichos de actividad matemática: «Ampliar la forma en que definimos el entorno de las matemáticas en el hogar temprano, reconociendo que los padres apoyan una gama más amplia de habilidades matemáticas que solo la aritmética.» (Zippert & Rittle-Johnson, 2020, p. 11). En concordancia, una gran parte de los estudios que hacen parte de esta revisión centran su análisis en la exploración del aprendiz de esos ambientes complejos creados por la familia, la cultura y la escuela que, aunque no necesariamente están orientados a la enseñanza de la matemática, conducen al desarrollo natural de las habilidades matemáticas del infante en la cotidianidad.
Algunos de los nichos matemáticos están delimitados por la creación activa de oportunidades de aprendizaje generadas por el adulto y dirigidas al niño:
El aprendizaje lúdico ofrece oportunidades para aumentar la conversación y la comunicación (Toub et al., 2018; Weisberg et al., 2016). Al fomentar la conversación entre los compañeros del niño y entre los niños y los cuidadores; las actividades de aprendizaje lúdicas fomentan la construcción de la base de la comunicación que es fundamental para el éxito académico posterior de los niños. (HassingerDas et al., 2020, p. 3)
En muchos casos el ambiente se enriquece de tantas maneras diferentes que la actividad del aprendiz puede ser soportada y orientada en diversas facetas mutuamente interconectadas, generando procesos fluidos naturales de desarrollo cognitivo:
Las experiencias de aprendizaje se pueden apoyar (o estructurar) en los niveles motivacional, afectivo, cognitivo y metacognitivo (Reiser & Tabak, 2014) mediante la implementación de indicaciones, sugerencias y preguntas. Estos mediadores (scaffolds) pueden describirse como fijos o adaptativos (Azevedo et al., 2004, 2005; Puntambekar & Hubscher, 2005). En el contexto de los entornos de aprendizaje apoyados por la tecnología, los soportes (scaffolds) fijos son elementos estáticos de la interfaz, mientras que los apoyos (scaffolds) adaptativos son adaptables para satisfacer las necesidades de los alumnos [énfasis agregados]. (Valle et al., 2021, p. 3)
Es crucial notar que existe una conexión intrínseca entre la disponibilidad de posibilidades de acción en el entorno próximo (affordances), la disposición sociocultural del ambiente por parte de los miembros avezados de la comunidad que quieren enseñar al infante mediando su actividad (scaffolding) y la exploración-reconocimiento (skilled responsiveness) del aprendiz de los patrones decisivos del quehacer en la práctica (Rietveld et al., 2018). Ello configura una dinámica triádica relevante para entender el desarrollo de conceptos.
Ahora bien, el método de revisión de este estudio permite una exploración transversal adicional, puesto que los estudios indagados fueron preclasificados de acuerdo con las palabras claves de las 4E. Entonces, ello permite examinar brevemente cómo es que ciertos asuntos relevantes se conciben relacionados con cada una de estas facetas de la cognición situada. Este análisis muestra sutiles diferencias que pueden ser orientadoras respecto a los intereses de los autores de las 4E (figura 4).
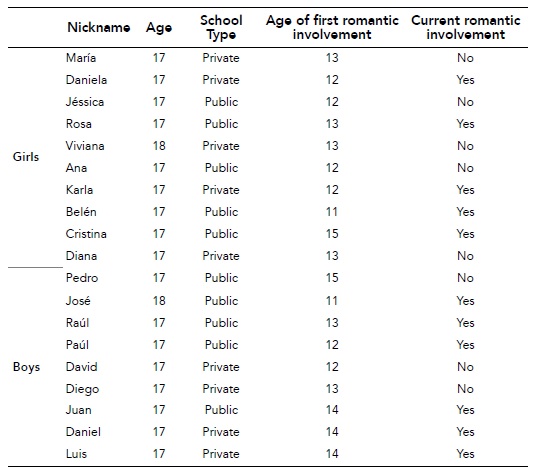
Figura 4 Relaciones entre las facetas de las 4E y los temas dominantes de estudios junto con las palabras claves más recurrentes
Como puede verse, aquellos estudios que enfatizan más el carácter extendido de la cognición se interesan más por la trayectoria sociocultural de los aprendices en prácticas conjuntas y se enfocan preferentemente en las estrategias de mediación con las cuales se introduce a los niños en contextos educativos en el aprendizaje de la matemática. Entre quienes están más interesados en el desarrollo de los conceptos y habilidades básicas suele predominar una orientación corporeizada. En los estudios que enfatizan la importancia del marco sociocultural y las dinámicas situadas del aprendizaje de la matemática el tema central tiene que ver la exploración activa de los niños de diferentes nichos matemáticos (desde la casa hasta el supermercado) en contextos socialmente complejos. Nótese lo iluminadora que es la concordancia entre temas emergentes en las teorías 4E y las palabras más recurrentes entre los estudios que hacen parte de la revisión (figura 4).
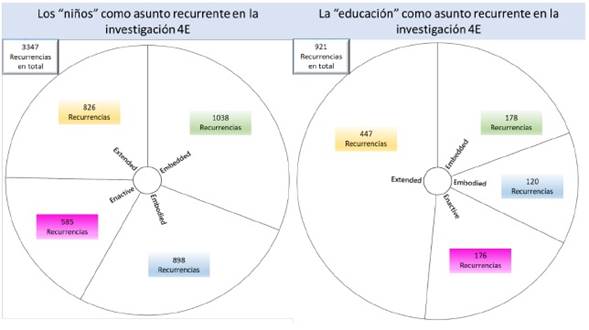
El sentido de cada una de las facetas de las 4E (embedded, extended, embodied, enactive) puede reconstruirse también atendiendo a los elementos internos de cada una de esas categorías. Una primera exploración útil puede lograrse simplemente mostrando las palabras en boga asociadas a los documentos así clasificados (figura 5). Lo que más resalta en cada nube de palabras son los componentes comunes (niño, matemáticas, aprendizaje, soporte, etc.), pero en la periferia de cada representación pueden verse términos reveladores del sentido de cada faceta en las teorías 4E: a) cognición extendida (gestos, tecnología); b) cognición incorporada (soporte, padres, actividades); c) cognición enactiva (juego, valor, exploración); y, d) cognición corporeizada (espacial, diseño, línea).

Figura 5 Términos más recurrentes en los estudios de cognición 4E sobre el aprendizaje de la matemática
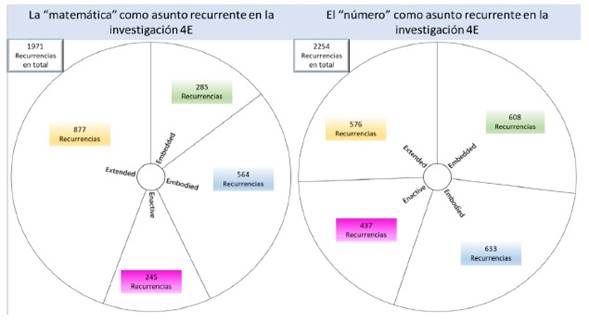
Finalmente, también puede observarse la asociación inversa para ver el peso que cada una de las 4E ha venido teniendo en la indagación de los asuntos relacionados con cada término clave. Así, por ejemplo, en el caso del tema de la numerosidad -que ya mencionamos atrás- sus términos centrales, matemática y número, han sido explorados más desde un enfoque que privilegia el carácter corporeizado y extendido de la cognición (figura 6).
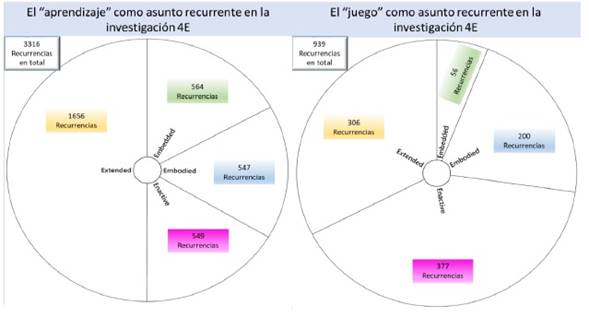
En el caso del juego, que como ya vimos es un asunto central en la exploración de nichos matemáticos cotidianos, la mayor cantidad de recurrencias se encuentran del lado de los estudios que exploran las facetas enactiva y extendida de la cognición (figura 7).
En lo que tiene que ver con los términos asociados a la trayectoria sociocultural y el andamiaje (niños y educación) puede anotarse la importancia de los estudios preclasificados en las facetas extendida e incorporada (embedded) de la cognición situada (figura 8).
Nótese que, más allá del simple conteo de palabras asociado con los términos relevantes en cada faceta, lo que se presenta en esta revisión son las coordinaciones interesantes dentro de tendencias de investigación (figura 4), lo cual nos acerca a los ejes de discusión que muy seguramente llegarán a ser centrales al abordar los temas relacionados con los términos listados.
Discusión
De acuerdo con los resultados de esta revisión, las teorías 4E han logrado abrirse espacio en la discusión sobre el aprendizaje de la matemática en cada uno de sus frentes, generando una visión alternativa de cómo promover el desarrollo intelectual. Se puede afirmar que las ideas del enfoque 4E se han adaptado de forma fructífera al ámbito educativo, promoviendo un tipo de reflexión en la que cada aspecto de la dinámica de aprendizaje se investiga de manera coordinada con otros que hacen parte del mismo sistema complejo.
Así, por ejemplo, para los investigadores interesados en la faceta extendida de la cognición, quienes se preocupan por desarrollar tecnologías interactivas y generar diseños de ambientes capaces de promover el aprendizaje, es cada vez más claro que sus esfuerzos están en relación directa con la experiencia subjetiva del aprendiz y con los objetivos socialmente articulados de las actividades dentro de las cuales se usan los dispositivos propuestos:
Las actividades de aprendizaje móvil que se percibieron como útiles, fáciles de usar y divertidas generaron mayores probabilidades de percepciones positivas sobre el aprendizaje móvil. La relación entre estas tres variables y las actitudes hacia el aprendizaje móvil puede servir como una guía de diseño para las sesiones de aprendizaje móvil. Si una aplicación es útil pero incómoda de usar, es posible que los usuarios no la acepten muy bien. De la misma forma, si una aplicación es útil y fácil de usar pero las actividades terminan aburriendo a los alumnos, entonces esta no sería muy bien recibida. (Fabian & Topping, 2019, p. 9)
Esta comprensión del carácter integrado de las cuatro facetas de la cognición (extendida, enactiva, incorporada y corporeizada) tiene el potencial para revolucionar nuestra comprensión sobre cómo incrementar el impacto social de la educación. El asunto estriba en notar el potencial formativo de la participación en prácticas cotidianas de aprendizaje que, tradicionalmente, fueron abandonadas por considerarse externas al ámbito intelectualizado del saber escolar. Esto es muy claro cuando se atiende a la faceta incorporada sociocultural en los estudios recientes:
Los niños pueden aprender y practicar una cantidad sustancial de lectura y matemáticas en el contexto de la compra de comestibles; por ejemplo, leer etiquetas y precios, contar, sumar y restar números de alimentos, escribir y verificar una lista de compras y mantenerse dentro de un presupuesto específico. (Leyva et al., 2017, p. 64)
Hay dos lecturas posibles de la cita anterior. En la visión intelectualista tradicional, las actividades del niño en el supermercado le permiten ejercitar sus habilidades y conceptos adquiridos mejor que en ambientes formalizados escolarizados. Desde el punto de vista 4E, el entorno del supermercado constituye un ambiente de aprendizaje en el que se adquieren las habilidades y conceptos necesarios para lidiar con problemas matemáticos. Hay una auténtica revolución liderada por los maestros de América Latina (Camelo et al., 2017; Cantoral & Reyes-Gasperini, 2014; Miranda & Gómez-Blancarte, 2018) en la que la adquisición de saber matemático ha dejado de ser una cuestión de transmisión de conceptos y algoritmos, para convertirse en un asunto de vinculación en actividades como parte de comunidades de práctica.
Es necesario indicar que existe una enorme diversidad de perspectivas en boga en el área: desde aquellas centradas en la creación de problemas (Malaspina, 2021) hasta los que enfocan la importancia del saber matemático en las comunidades (Aroca, 2015). No se puede ignorar la contribución cada una de estas aproximaciones. Más aún, es preciso señalar los muchísimos puntos de convergencia entre estas aproximaciones y el enfoque de las 4E; por ejemplo, en lo que atañe a las facetas enactiva y socialmente incorporada de la cognición:
Nos demuestran los Calibradores el desarrollo de un sistema de comunicación numérico gestual muy complejo, basado en los tiempos, en el ritmo de trabajo que está en función de las luces del semáforo, de las ganancias diarias del transporte urbano de pasajeros, de la competencia, entre otras variables previamente descritas; cuya organización o algoritmo, lenguaje, sintaxis y procedimiento, marca diferencias con el algoritmo escolar, lo que una vez más muestra que hay un cálculo flexible, que no solo hay una forma de calcular (Aroca, 2015, p. 253)
Nótese en la cita anterior del estudio etnomatemático conducido por Aroca la profunda sintonía con los reclamos de la cognición enactiva acerca de la importancia de lo que sucede en tiempo real durante un problema matemático. Apúntese también que esta misma cita conduce a un diálogo fructífero con los maestros cuya perspectiva se centra en la creación de problemas. Queda claro que el impacto social del aprendizaje matemático no es algo que deba buscarse como un agregado adicional a los procedimientos e instituciones formalizadas para la enseñanza, sino que más bien está atado intrínsecamente a la construcción de modelos educativos que integren la matemática a la vida cotidiana de los aprendices.
Esta última reflexión nos conduce directamente a las repercusiones de esta revisión en la situación actual. El escenario de la pospandemia parece conducir ineludiblemente a un cambio en el tipo de actividades de enseñanza-aprendizaje de la escuela tradicional (Castro et al., 2020; Piñeiro & Vásquez, 2021). La situación en la cual un maestro reproduce algoritmos en un tablero para niños atentos a su desarrollo ha pasado a ser solo una posibilidad dentro de una innumerable gama en las que (conforme con lo que hemos venido mostrando) los niños pueden tener un rol más o menos activo, en involucramientos directos o indirectos, en relación con nuevas mediaciones tecnológicas o en contacto con artefactos culturales tradicionales, en situaciones divertidas, serias o, incluso, problemáticas.
La apertura de oportunidades generada por la transformación de la escuela puede conducir a los docentes al vértigo. Tiene todo el sentido del mundo sentir un poco de aprensión dada la dinámica cada vez más fluida de la relación interpersonal en el eje enseñanza-aprendizaje. Las ideas de la cognición 4E tienen el potencial para orientarnos en los momentos más abrumadores frente a los muchos aspectos de la complejidad de la enseñanza:
Para la actividad y el aprendizaje de las matemáticas, este encuadre destaca el interjuego entre las configuraciones materiales y las prácticas históricamente sedimentadas de una arena, por un lado, y la actividad dinámica y continua de los participantes, por el otro. Prestar atención a cómo los alumnos editan los escenarios en la actividad matemática proporciona una comprensión de los procesos de aprendizaje como un conjunto de contingencias incorporadas en un complejo de relaciones materiales, sociales y disciplinarias. (Kelton & Ma, 2018, p. 179)
En ese orden de ideas, y considerando el retorno a la presencialidad de las instituciones educativas en el marco de la pospandemia, diversos organismos multilaterales como The World Bank, Unesco y Unicef (2021) han enfatizado la importancia de diseñar estrategias eficientes y de calidad para todos los estudiantes. Así, García (2020) refiere la necesidad de acciones en cinco ejes: «1) recuperación del aprendizaje; 2) mantener la permanencia de los estudiantes y su conexión con la escuela; 3) esquemas de aprendizaje bimodales; 4) formación de maestros; y 5) acompañamiento a las familias» (p. 22).
Surge entonces la pregunta: ¿cómo articular estos desafíos en relación con los elementos conceptuales de las 4E para el diseño de estrategias pedagógicas y didácticas que permitan cualificar los procesos de enseñanza-aprendizaje? A continuación, se presentan algunos aportes.
En el primer eje de recuperación del aprendizaje es fundamental medir los niveles actuales de aprendizaje en matemáticas, para así obtener un panorama real de las fortalezas y debilidades de los estudiantes, de manera que sea posible diseñar planes de remediación en matemáticas teniendo en cuenta los niveles educativos. En ese sentido, desde una perspectiva extendida de la cognición, es relevante diseñar artefactos y ambientes de aprendizaje físicos y virtuales que puedan ser utilizados en procesos de evaluación en el aula, evaluaciones nacionales e internacionales. Para mencionar un ejemplo, en el marco de la virtualidad suscitada por la pandemia surgió la Olimpiada Internacional de Matemática en Educación Primaria (Mora, 2021), que tiene como uno de sus objetivos generar recursos que promuevan la mejora en la calidad de la educación matemática en diversos países. En estas olimpíadas participan estudiantes de 4º, 5º y 6º grado de primaria de cerca de 14 países de América Latina, Centroamérica y Europa.
En cuanto al segundo eje, que consiste en garantizar la permanencia de los estudiantes y su conexión con la escuela, es preciso fomentar la continuidad de los aprendizajes matemáticos obtenidos en casa durante la pandemia, en estrecho vínculo con las prácticas matemáticas en escenarios formales e informales y con los saberes del aula de clase. Así, se hace necesario, desde un enfoque incorporado de la cognición, que las actividades de aprendizaje estén articuladas con los saberes de la tradición cultural en la que los niños participan. Por ejemplo, se pueden propiciar en casa ambientes informales y formales de aprendizaje; en el primer caso se trata de experiencias cotidianas espontáneas (como conteo de elementos, asistir al mercado, clasificar objetos en la habitación) las cuales, si bien no tienen una intencionalidad académica específica, son contingentes a las condiciones espacio-temporales de las situaciones y a las interacciones padres-hijos. Los ambientes formales de aprendizaje requieren planeación explícita, conciencia de los padres sobre la enseñanza de uno o más tópicos matemáticos concretos, estrategias organizadas y reserva de tiempo para la realización de actividades con sus hijos (Cahoon et al., 2017). Asimismo, desde la vinculación docente con los aprendizajes tanto de la escuela como del hogar, se han diseñado proyectos de investigación que se han materializado en recursos digitales como «Aprender y enseñar matemáticas desde casa» (UED, 2022)
En el tercer aspecto de esquemas de aprendizaje bimodales, García (2020) menciona que es necesario
un diseño pedagógico que combine procesos de enseñanza-aprendizaje de manera presencial y no presencial y que incorpore la tecnología disponible en el corto plazo para poderle llegar a todos los estudiantes (…). La meta en el corto plazo es asegurar que, mientras las escuelas estén cerradas o en aperturas parciales, los estudiantes reciban un paquete educativo que garantice como mínimo el acceso a contenidos de calidad (vía digital, por televisión, radio o impresos), interacción y retroalimentación con el maestro (vía digital, por redes sociales, teléfono, o presencial cuando se pueda abrir) y materiales (impresos o digitales) para poder realizar las actividades de aprendizaje correspondientes (…). Por supuesto que en el mediano plazo el ideal es contar con plataformas digitales que permitan en un mismo espacio compartir contenidos y tener interacción entre estudiantes y docentes [énfasis agregado] (p. 24).
Este compartir en un mismo espacio y tener interacción docente-estudiante en tiempo real (planteamiento afín con la perspectiva enactiva de la cognición 4E) se ha ido recopilando en investigaciones que documentan el diseño de recursos digitales desarrollados durante la pandemia que posibilitan el aprendizaje de la matemática en línea (Scott, 2021) o el desarrollo de programas de televisión abierta diseñados para apoyar diariamente en matemáticas a niños de grado iniciales, enfatizando el uso del texto escolar oficial y la interacción docente-estudiante (Olfos et al., 2021). También es importante, por ejemplo, incorporar los aprendizajes obtenidos en juegos matemáticos digitales para fortalecer los procesos en el aula y las conexiones matemáticas (Moyer-Packenham et al., 2019).
En el cuarto aspecto, referente a la formación de maestros, se requiere «desarrollar un plan de formación y acompañamiento a los maestros que los entrene en las competencias tecnológicas y pedagógicas que se requieren para la implementación de las estrategias (a distancia o bimodales) que se llevarán a cabo en los siguientes meses» (García, 2020, p. 26).
En ese sentido, el enfoque de las 4E se puede vislumbrar en trabajos recientes de docentes en formación durante la pandemia. Para citar algunos ejemplos, Vargas et al., (2021) realizó un trabajo en torno a las producciones de futuros profesores durante el segundo semestre de 2020. El proceso se realizó usando la metodología de aprendizaje basado en proyectos, propiciando el descubrimiento de los vídeos digitales acerca de contenidos de geometría como formas novedosas de producir conocimiento en la formación del profesorado. Cao et al. (2021) emplearon un modelo de tetraedro didáctico de cuatro componentes (maestro, tecnología, estudiante y matemáticas) para indagar la percepción docente sobre la instrucción en línea en el aprendizaje matemático. Entre las conclusiones obtenidas se documenta la reorganización de métodos de enseñanza en interacción docente-estudiante, ampliar el uso de la tecnología en las interacciones y repensar la manera en que se dan dichas interacciones tanto a nivel presencial como virtual.
El quinto aspecto alude al acompañamiento, orientación y apoyo que han de recibir las familias en los procesos académicos, en prácticas parentales y la promoción del bienestar emocional en sus hijos. Teniendo en cuenta precisamente el componente afectivo, la arista corporeizada de la cognición puede contribuir en el trabajo con padres de familias. Así, Distefano et al. (2020) mencionan que los padres con mayores niveles de ansiedad matemática reportaron mayores experiencias emocionales negativas alrededor del ambiente de trabajo en casa cuando debían ayudar a sus hijos con tareas en casa.
En síntesis, las ideas de la cognición 4E pueden reorientar la investigación, la reflexión pedagógica y la planeación didáctica conduciendo la actividad docente de nuevo a su hogar originario; es decir, atrayendo la atención del docente y también la del aprendiz a lo que está ocurriendo en el ambiente compartido y a la actividad del otro que es tan significativa para avanzar juntos.